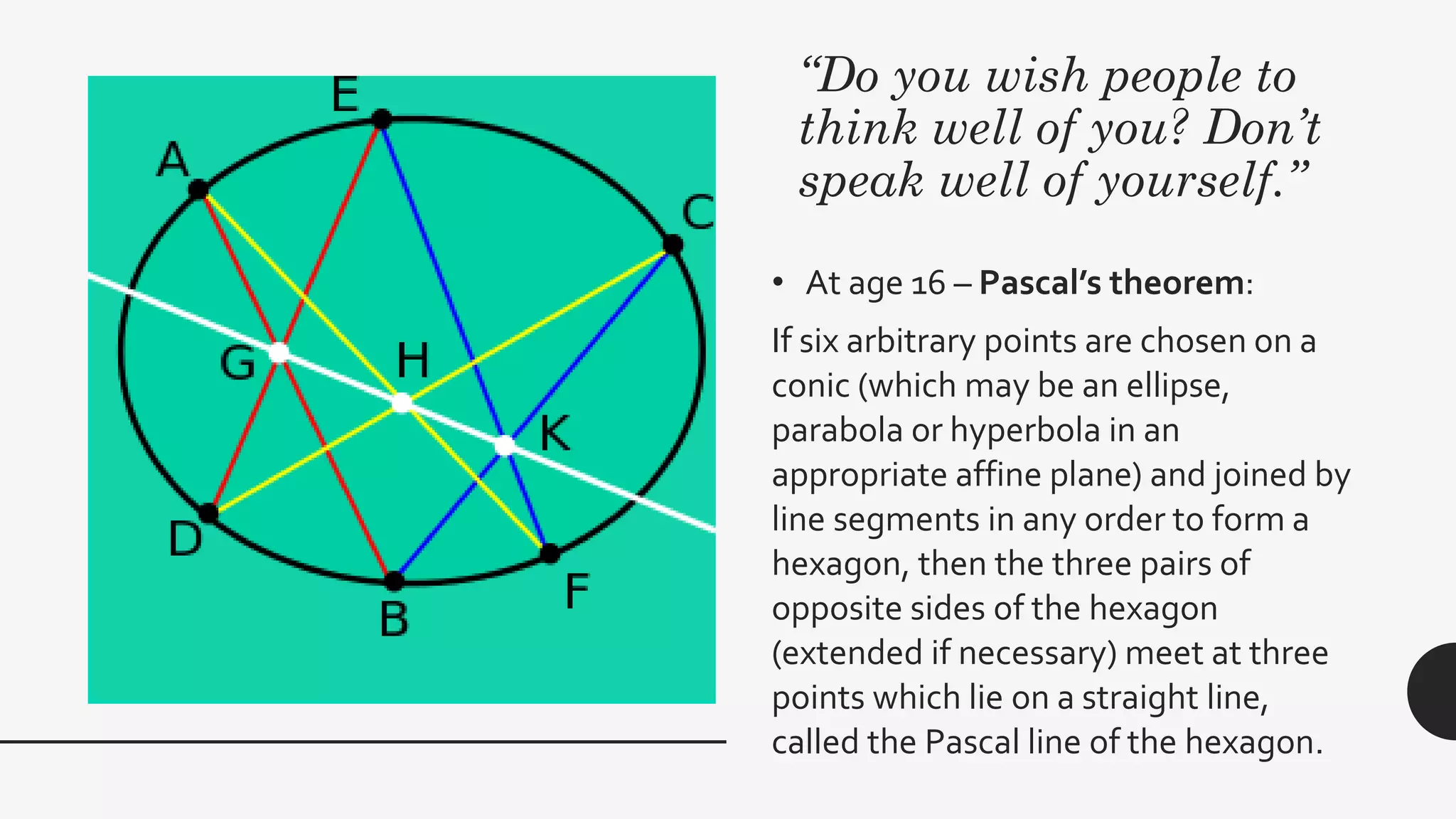
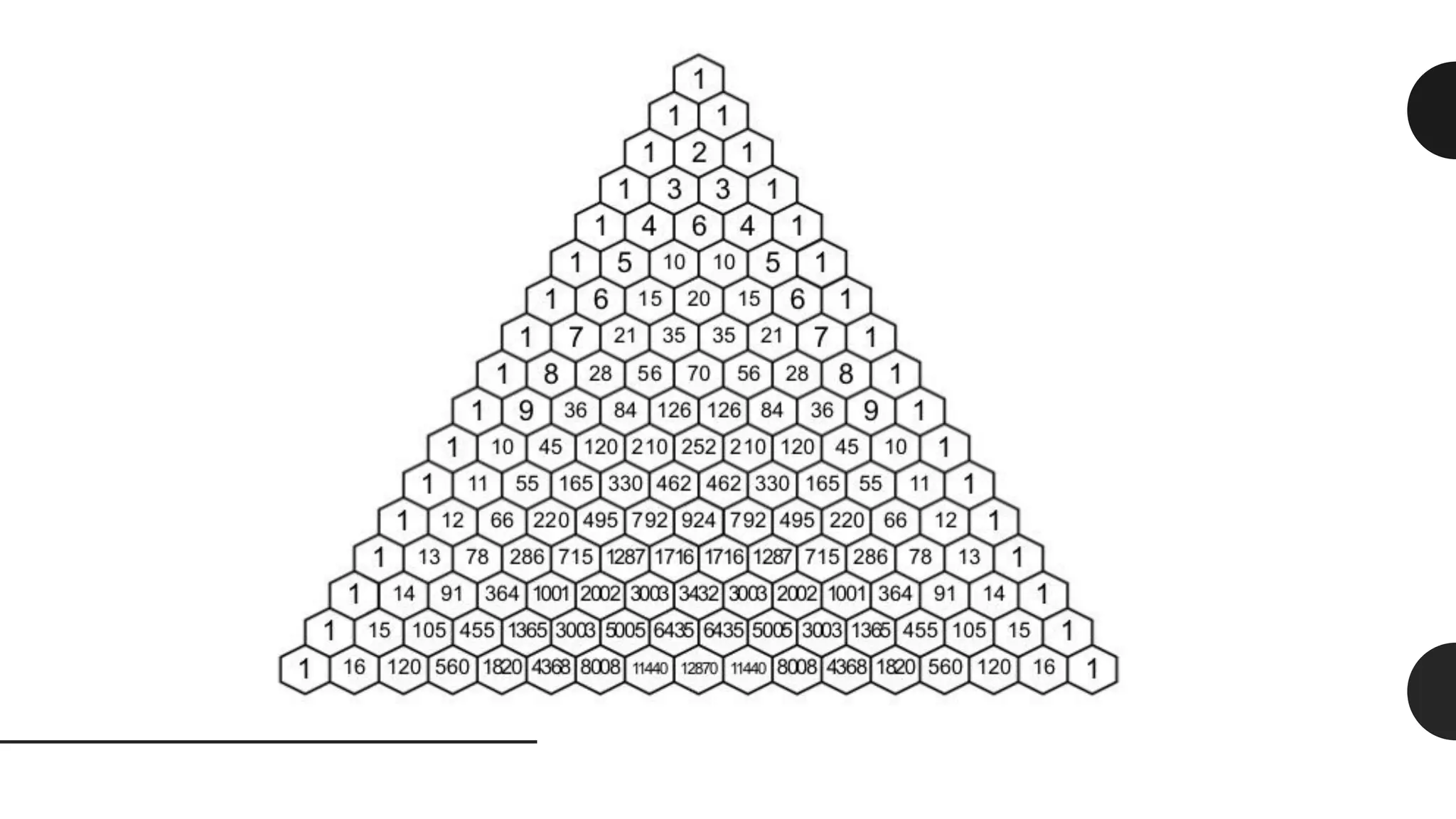
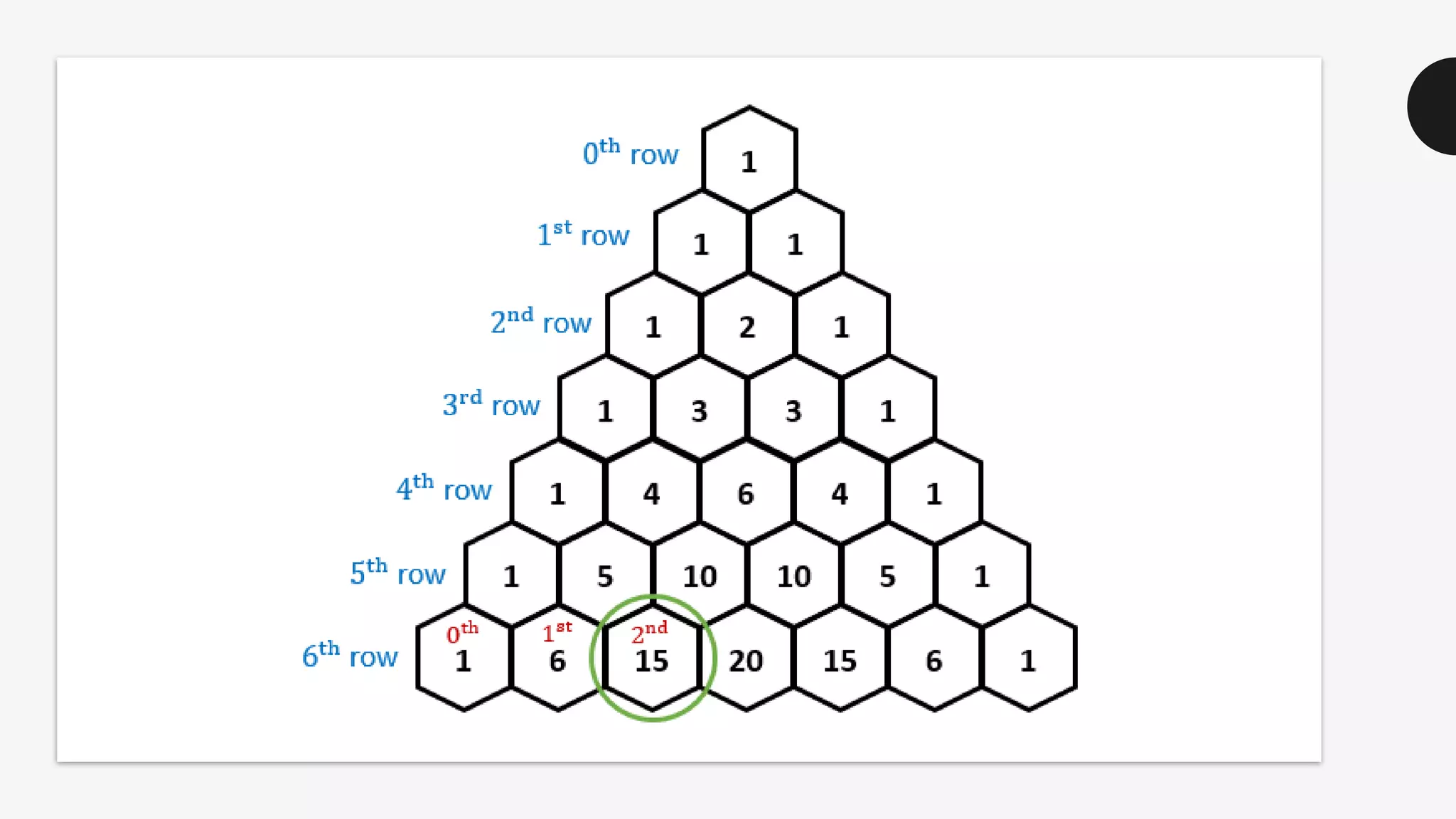
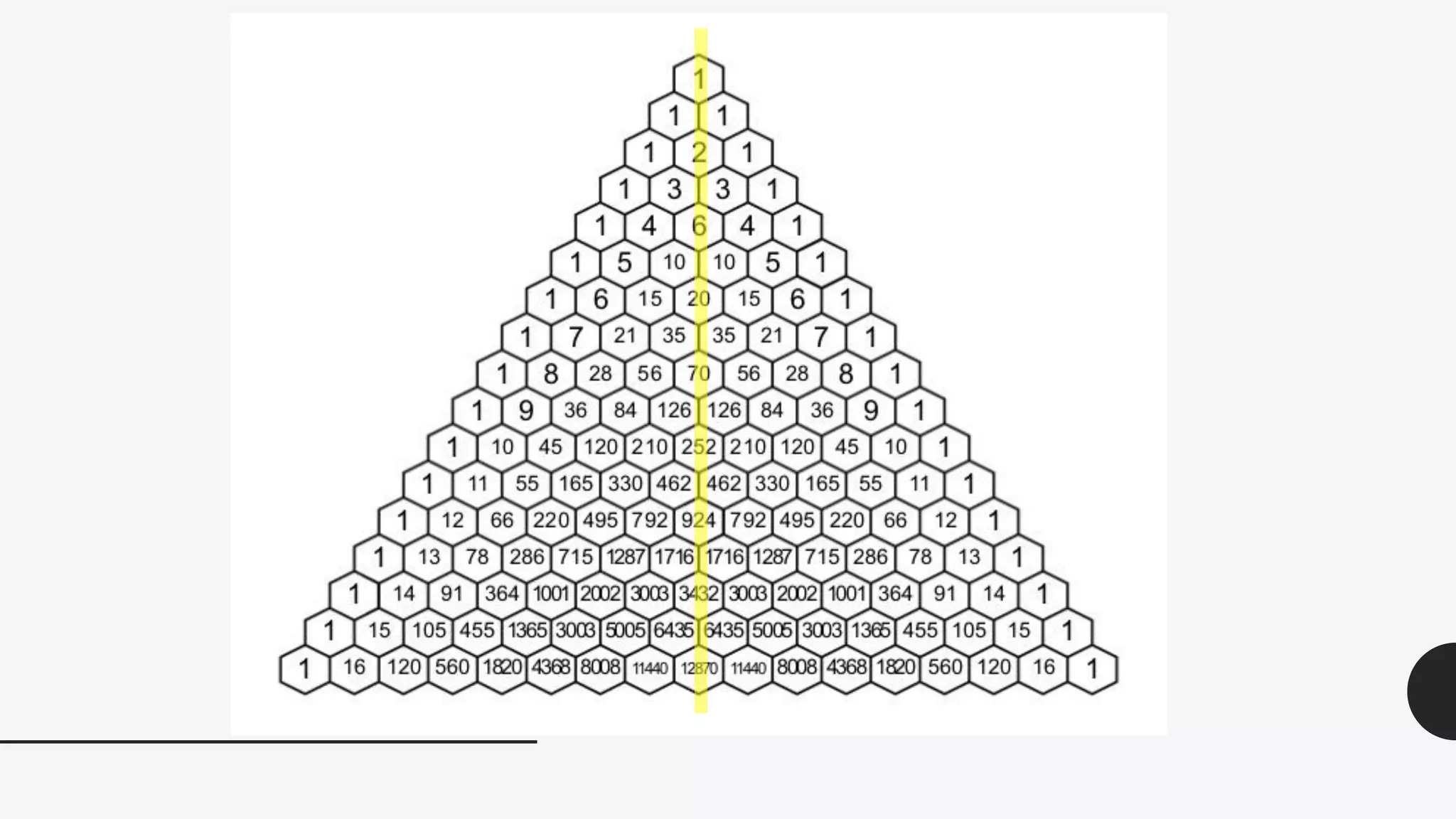
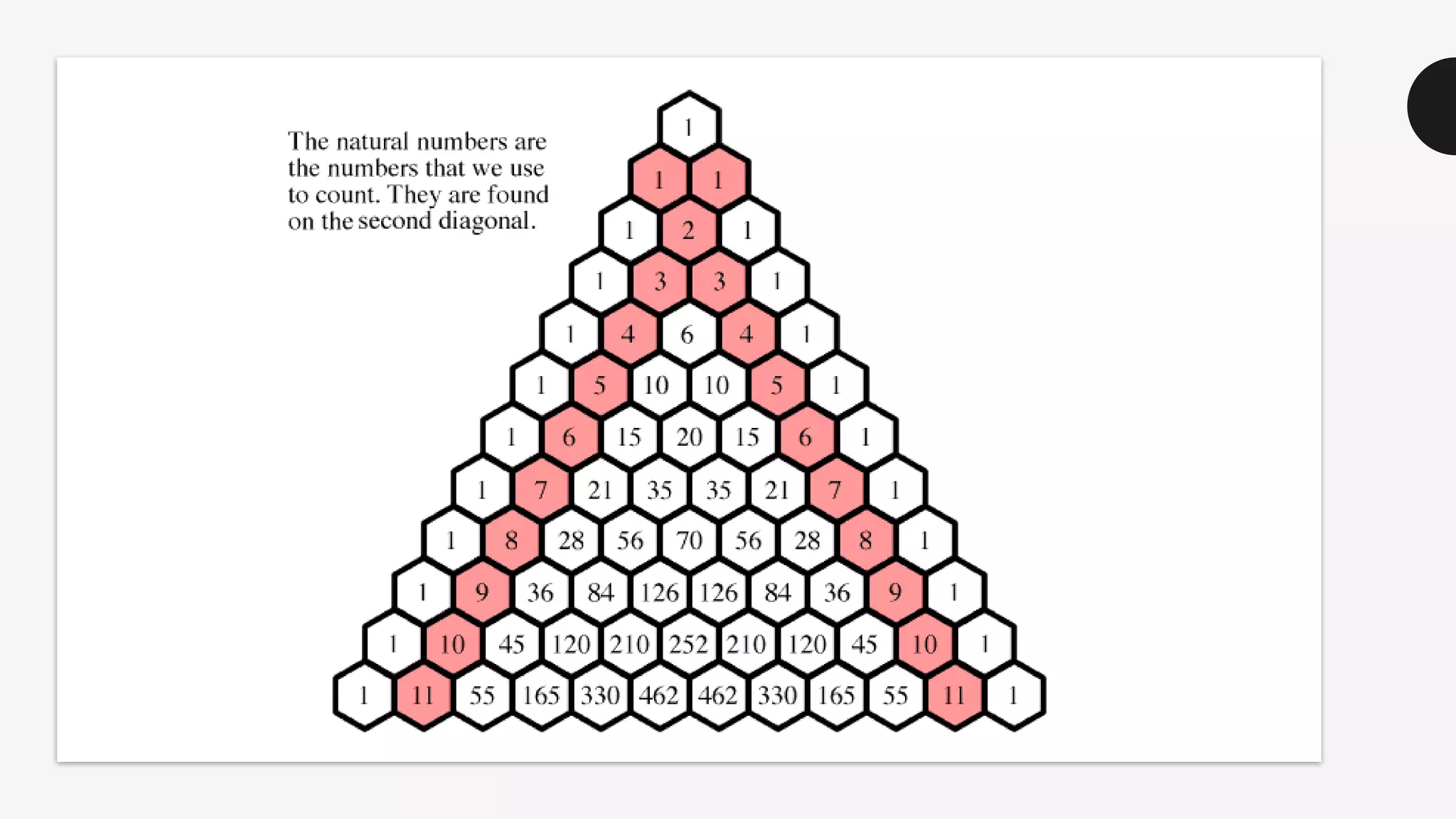
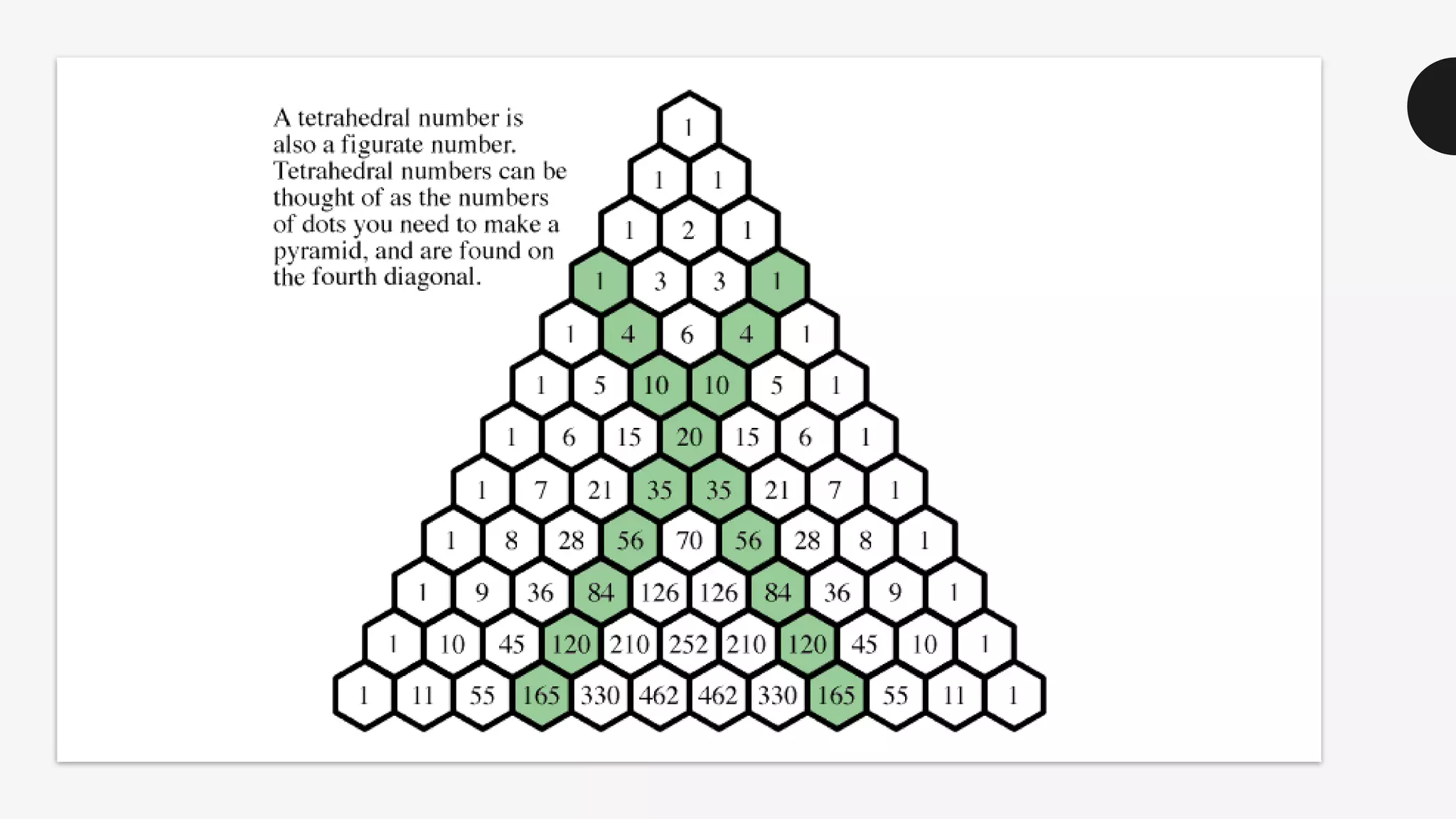
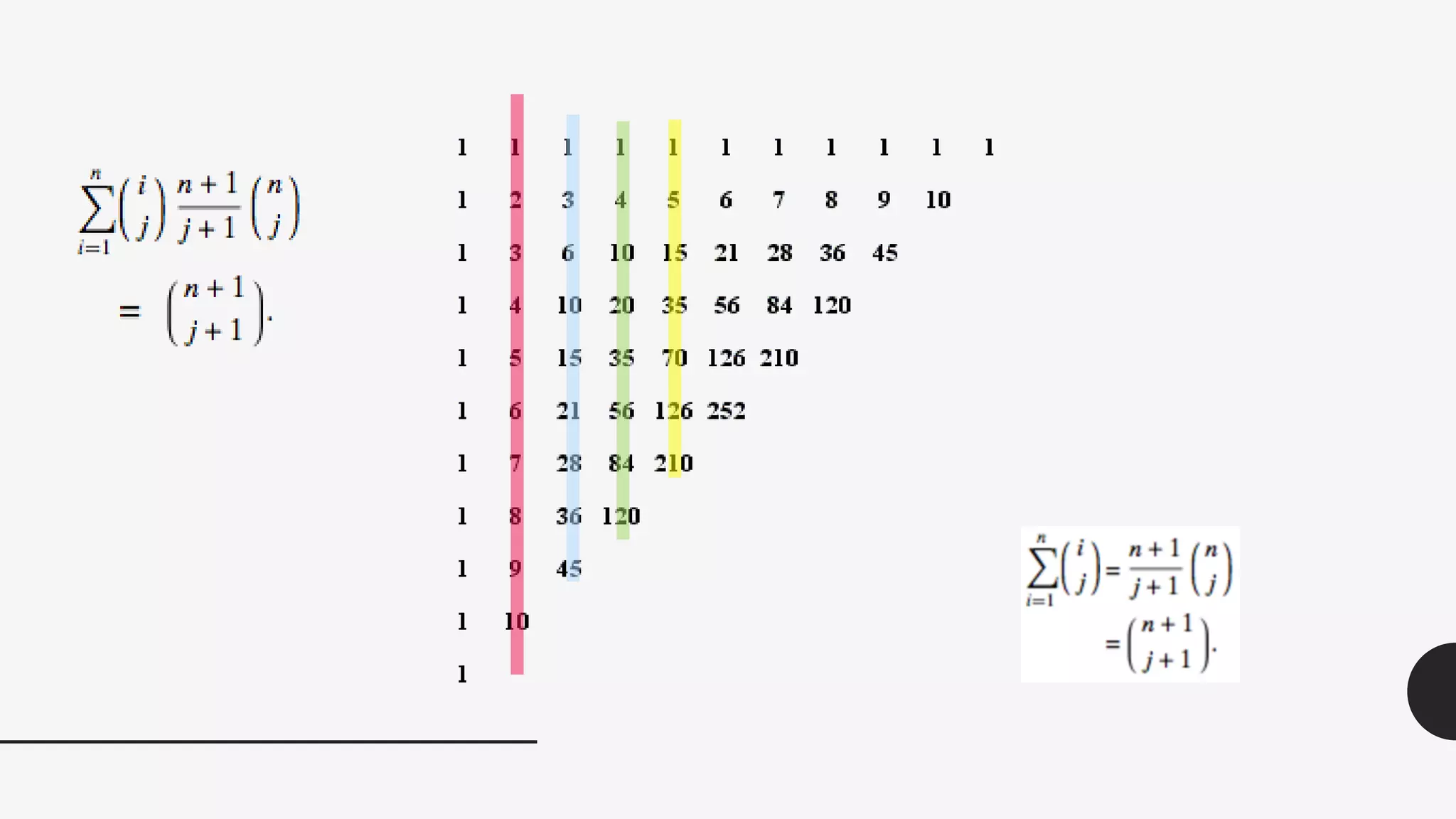
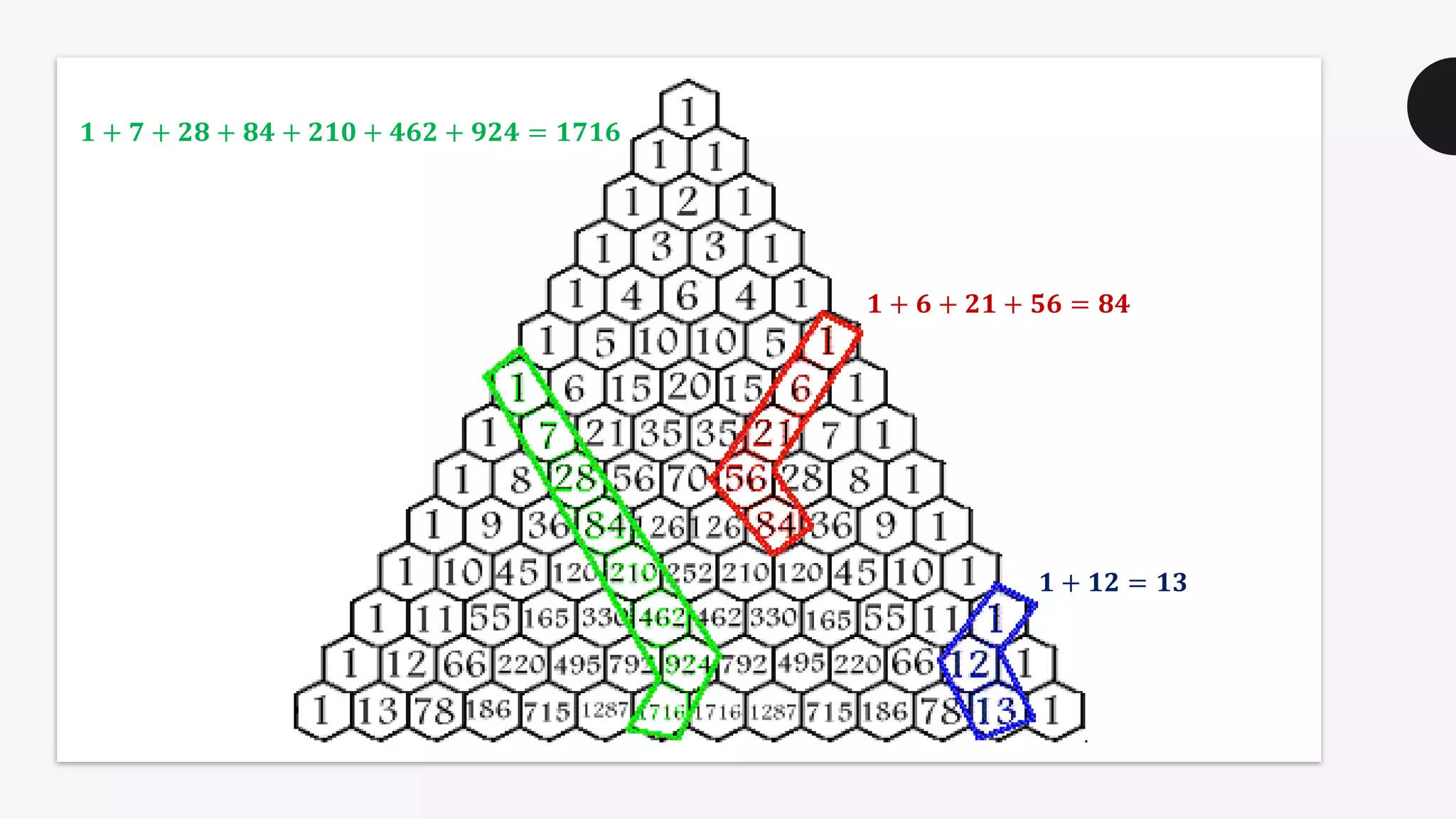
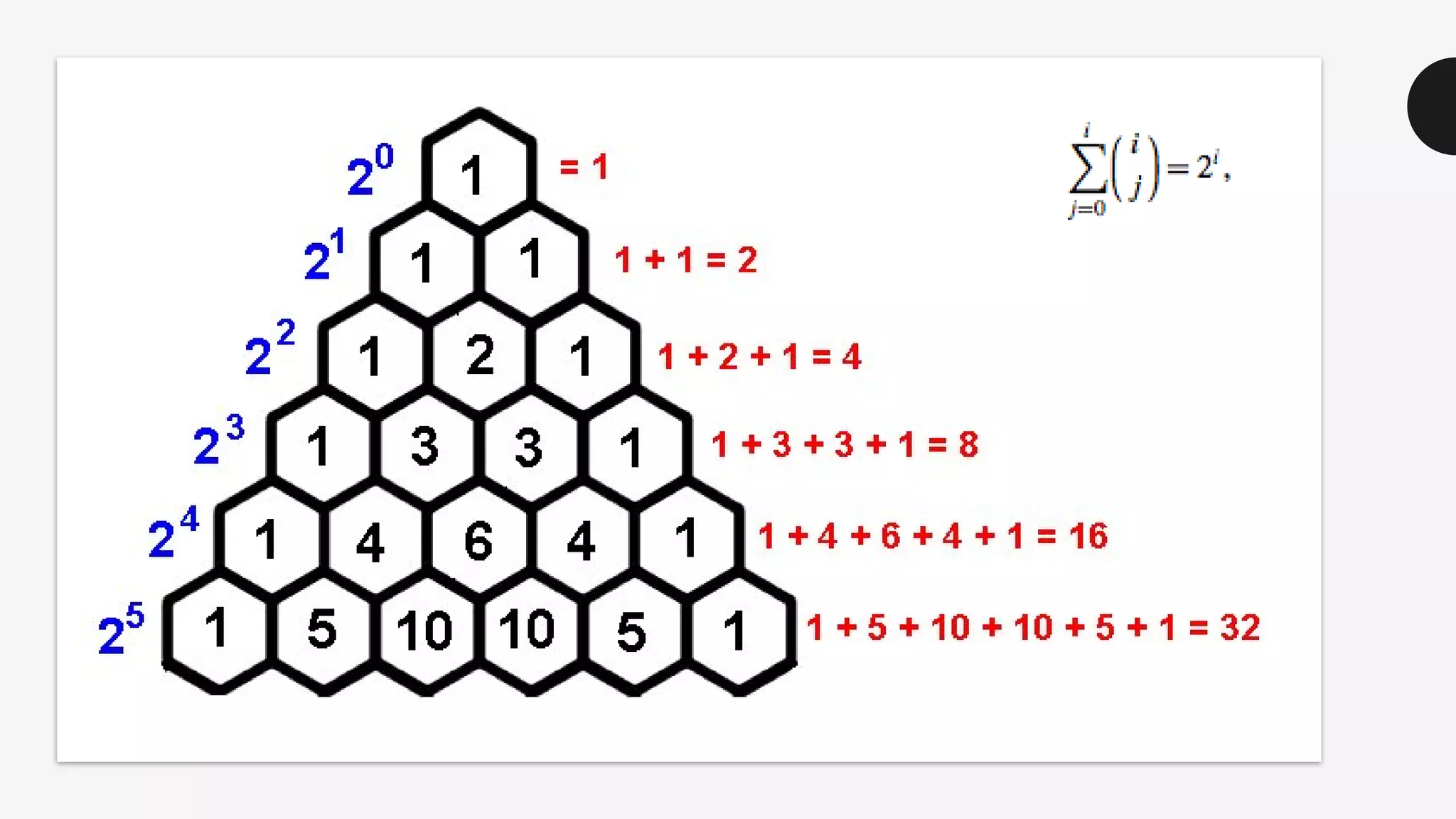
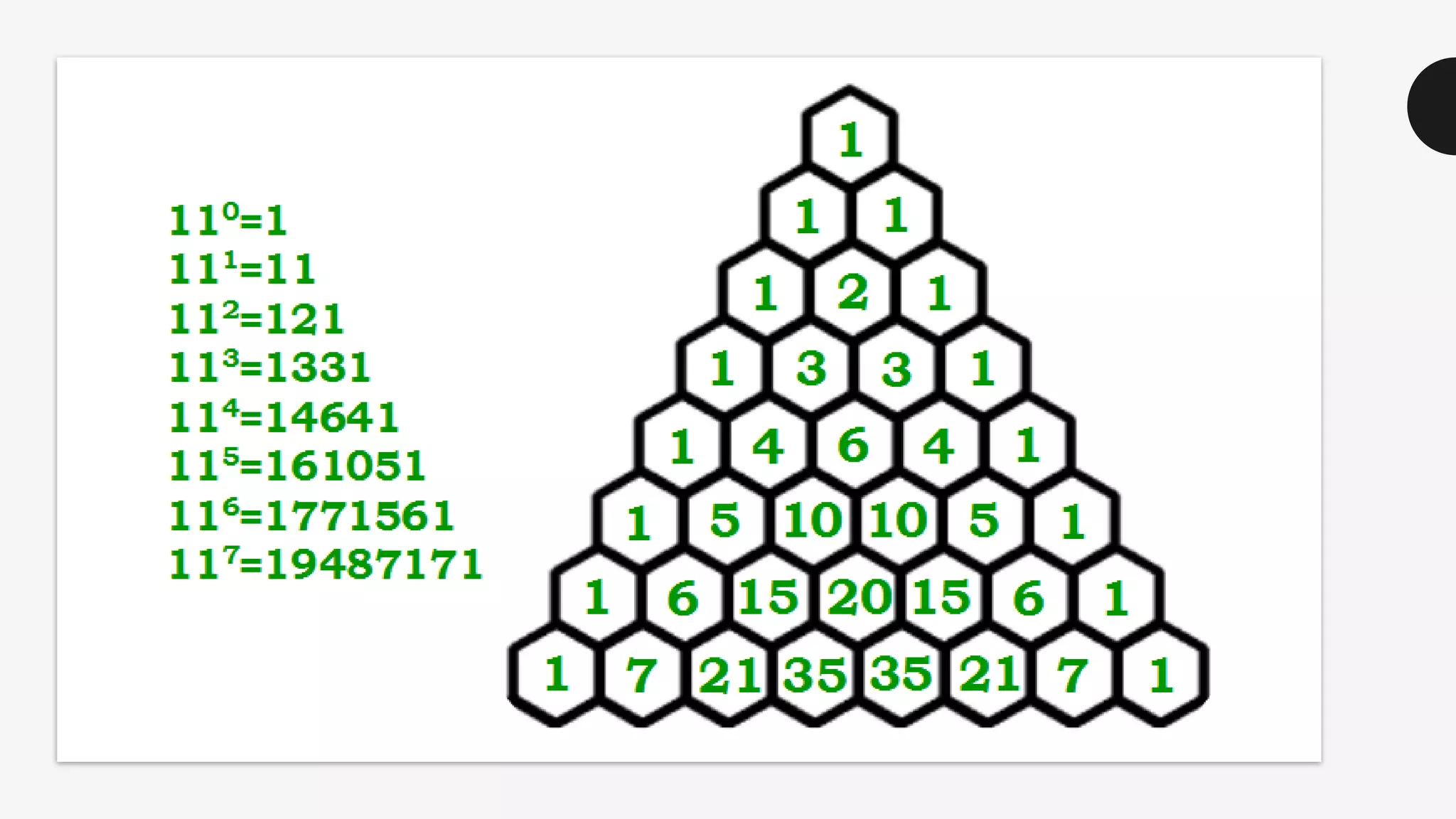
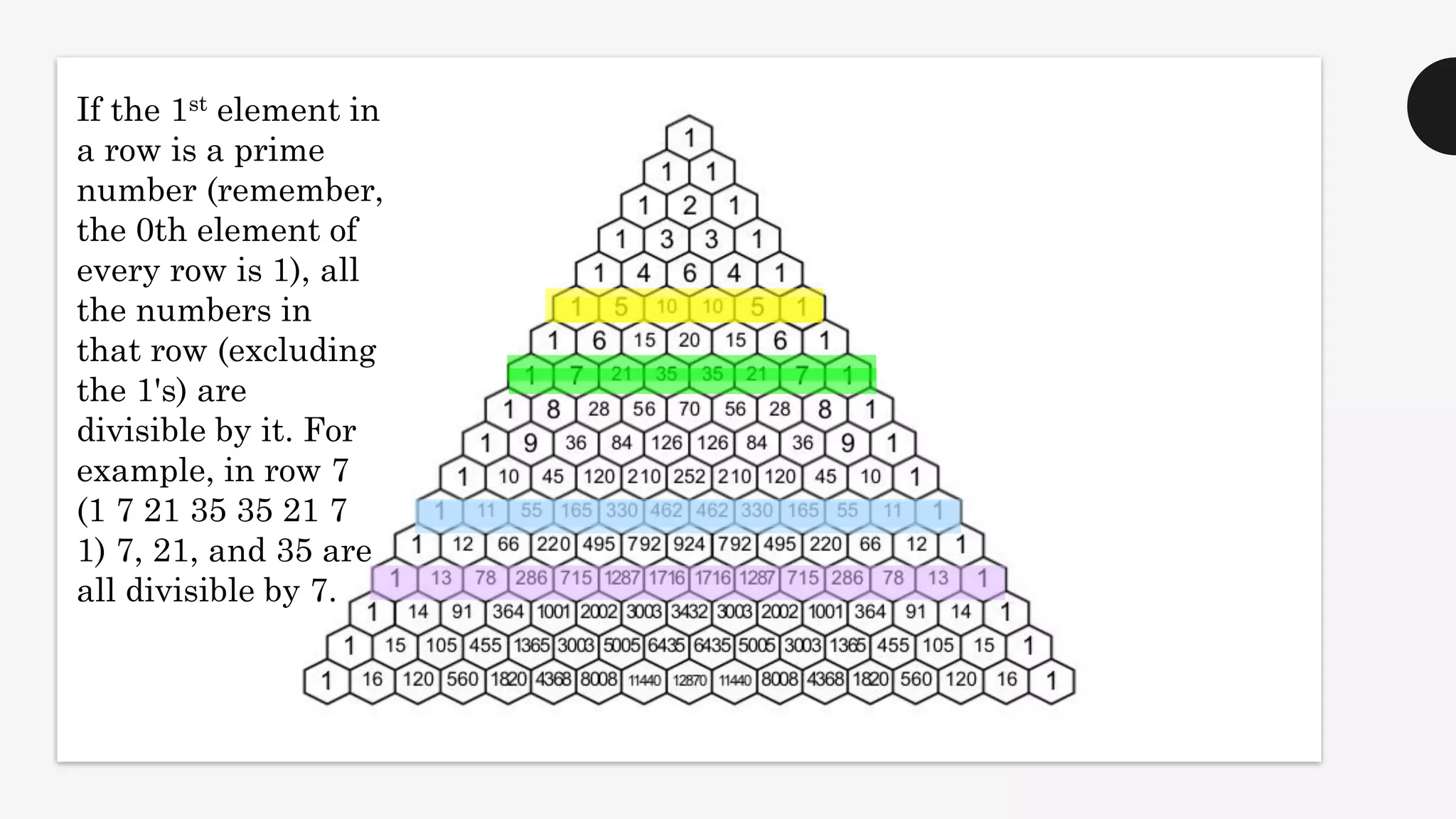
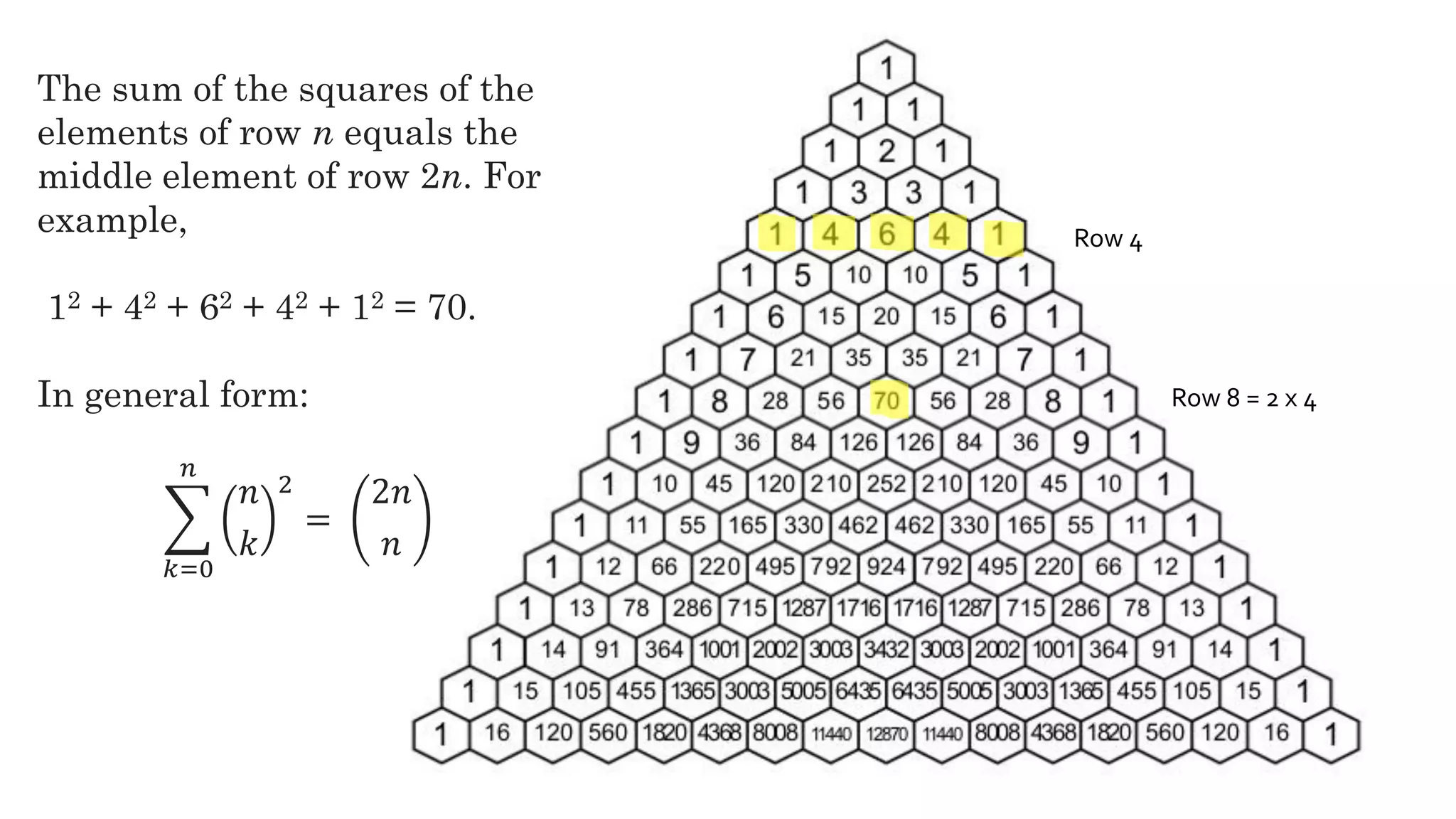
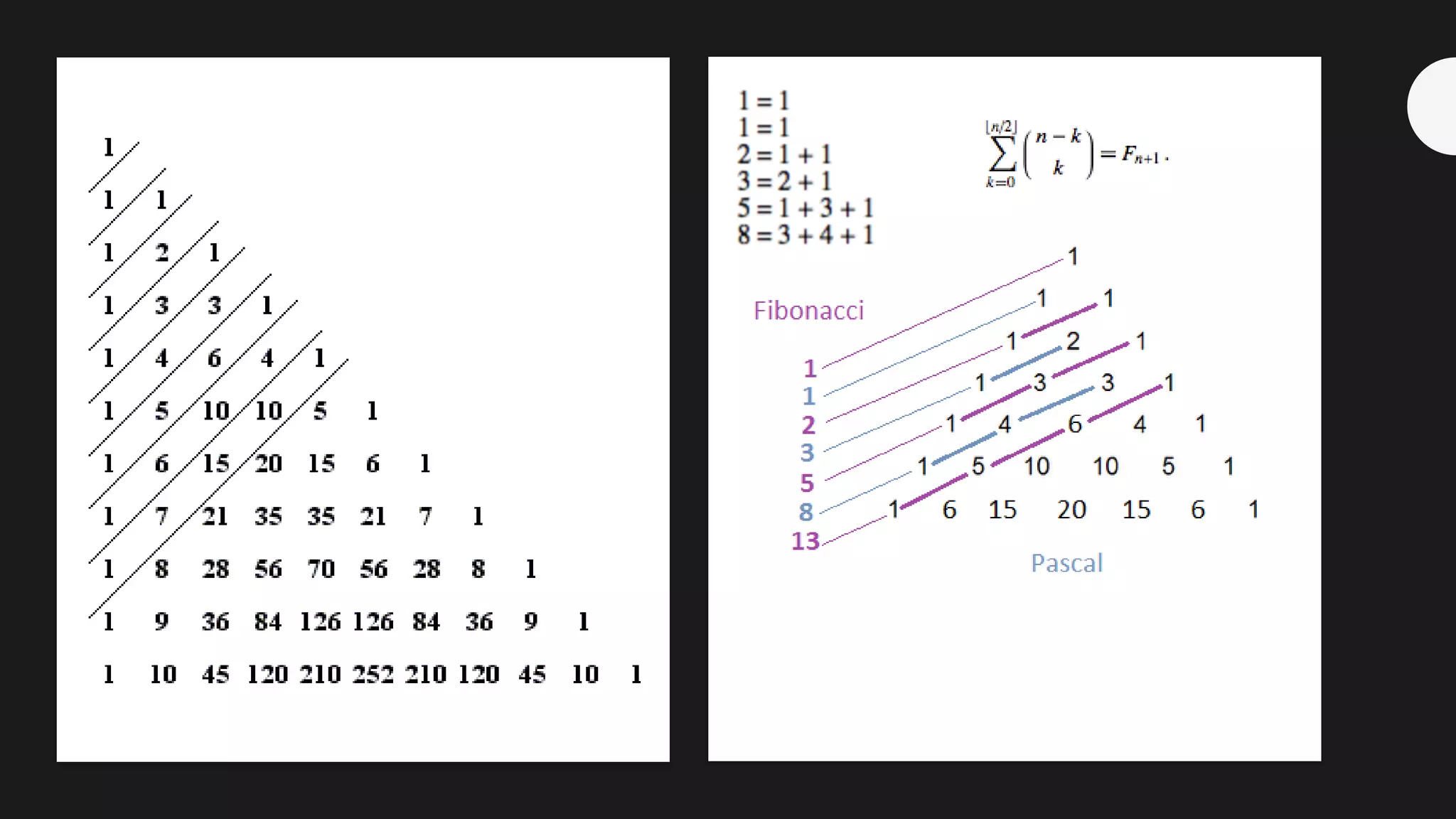
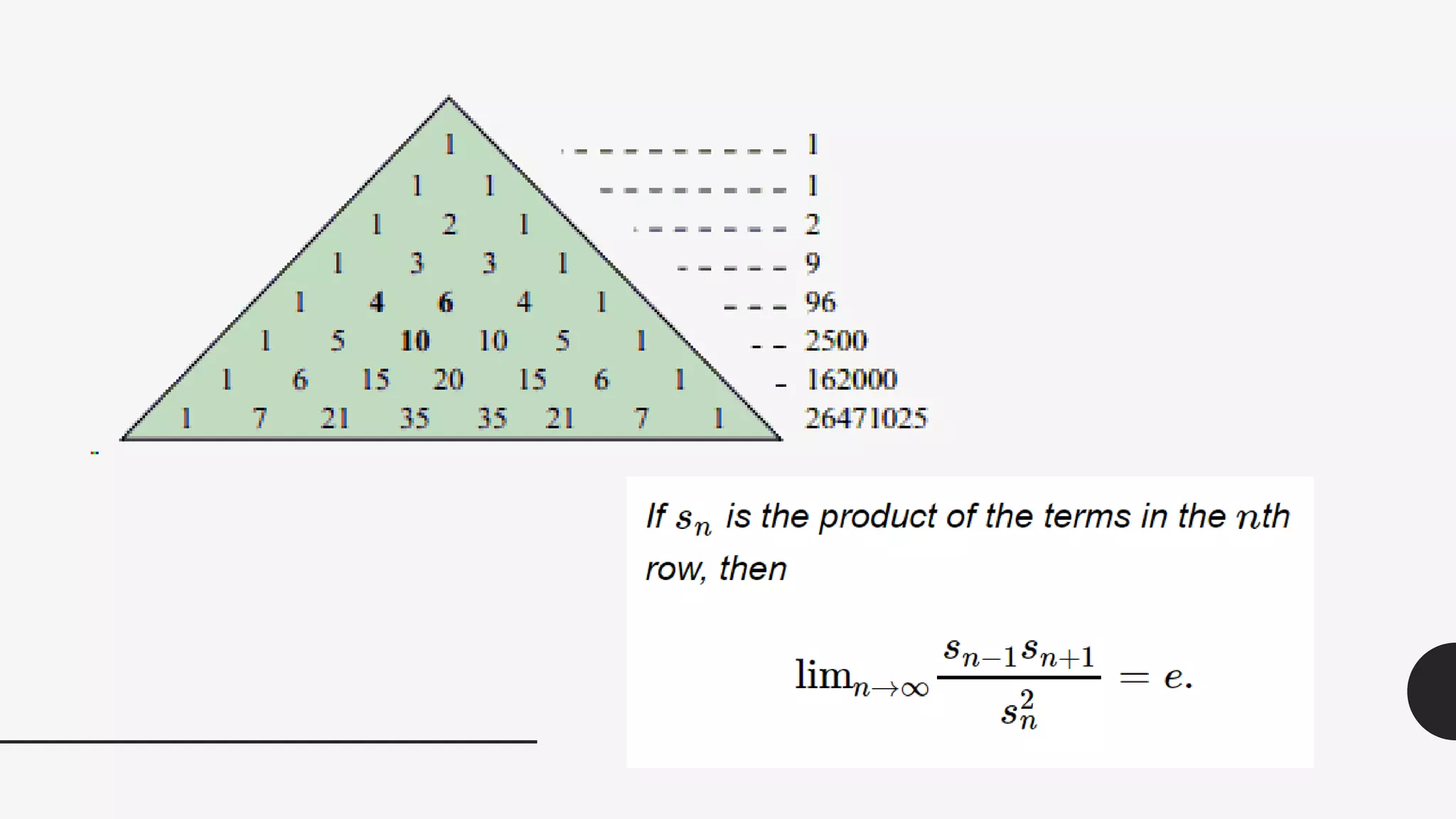
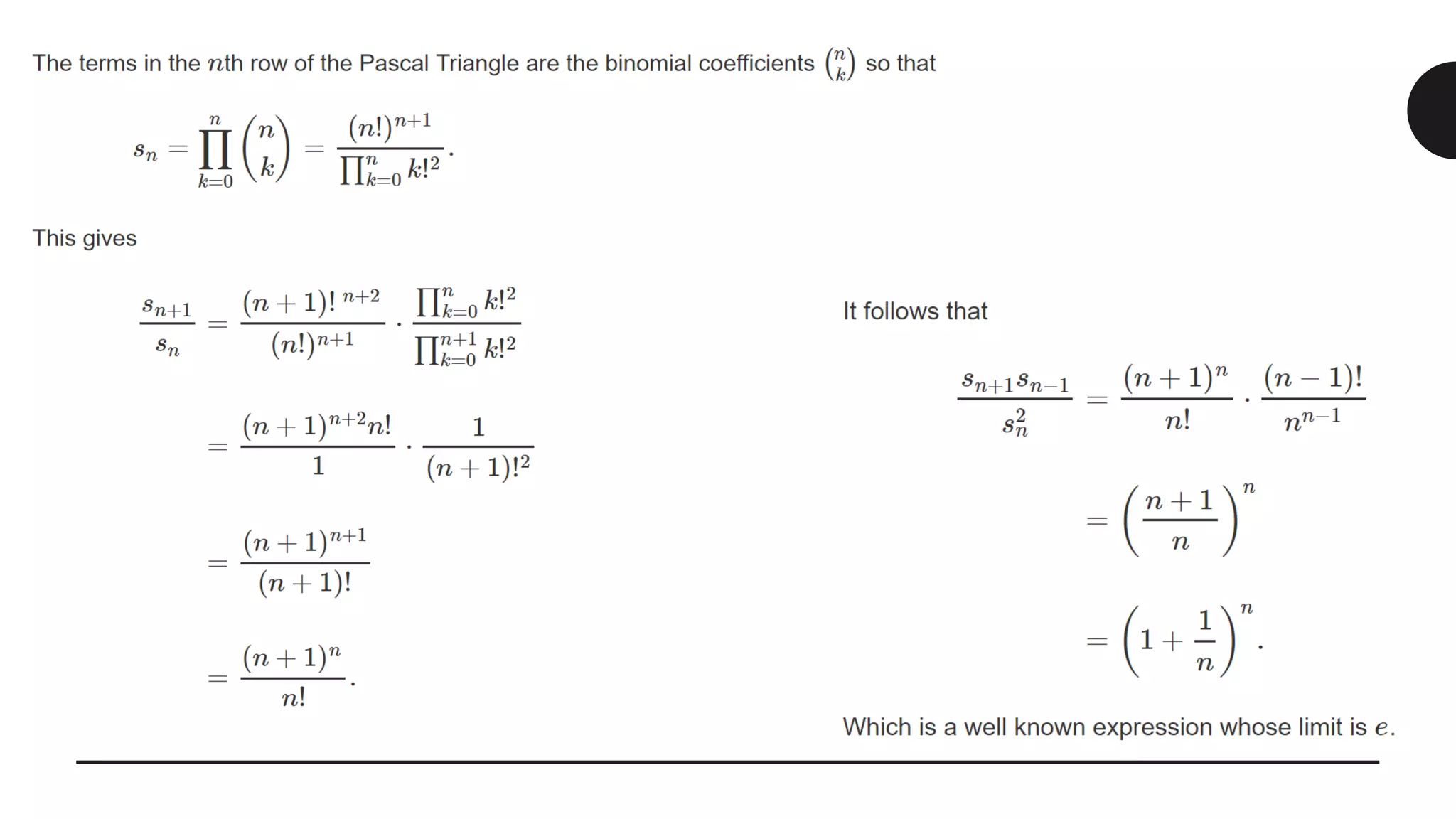
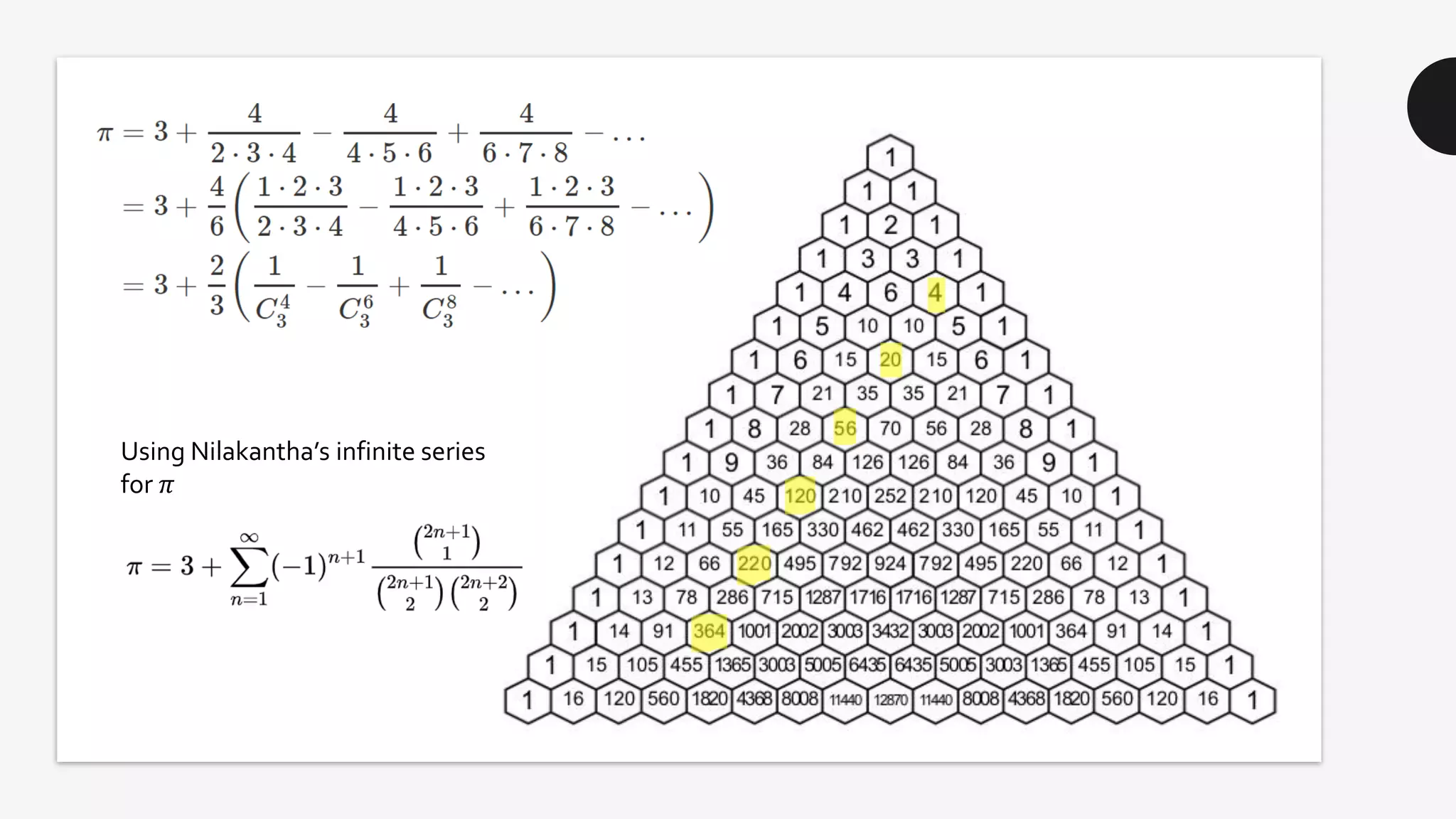
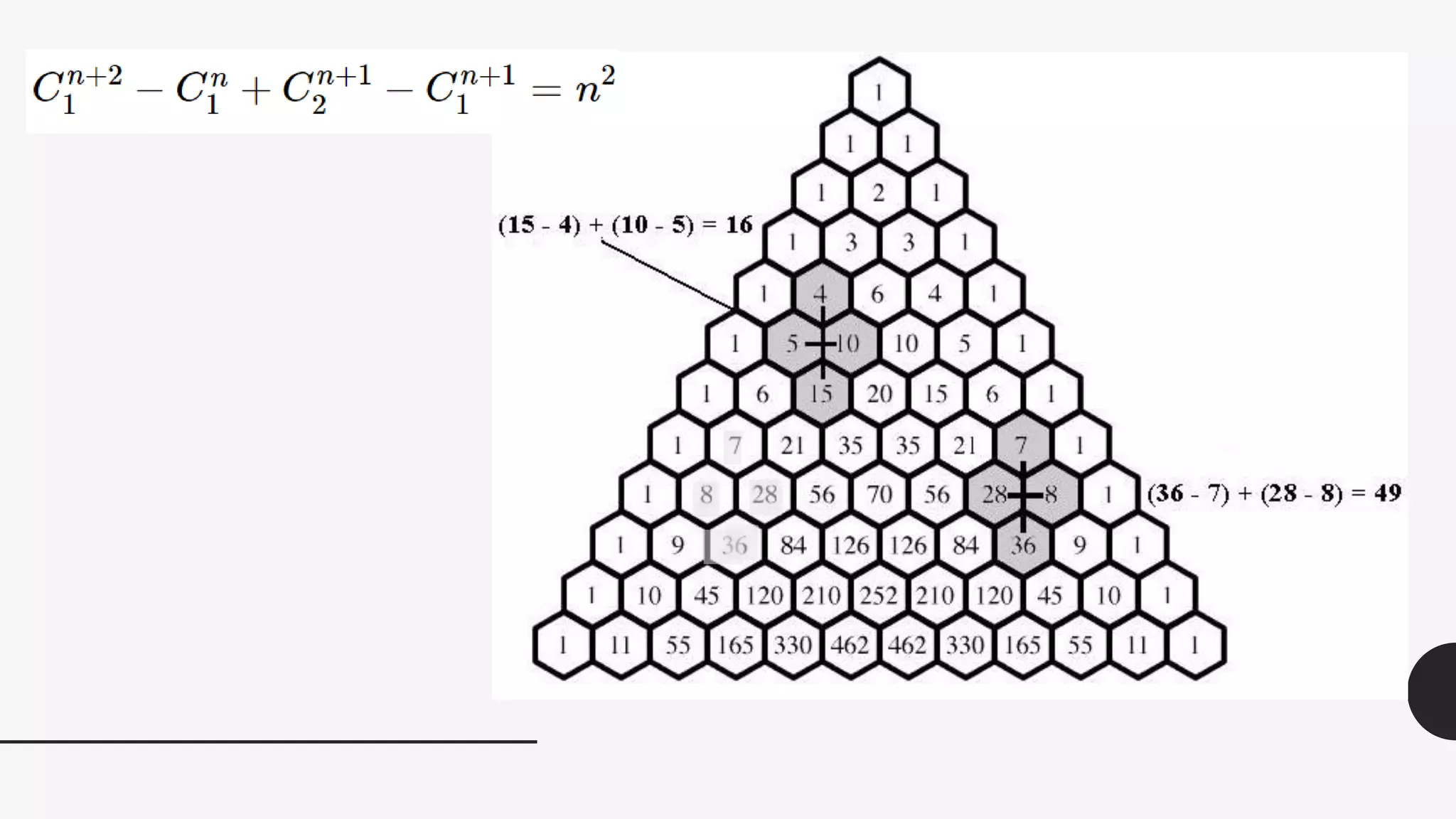
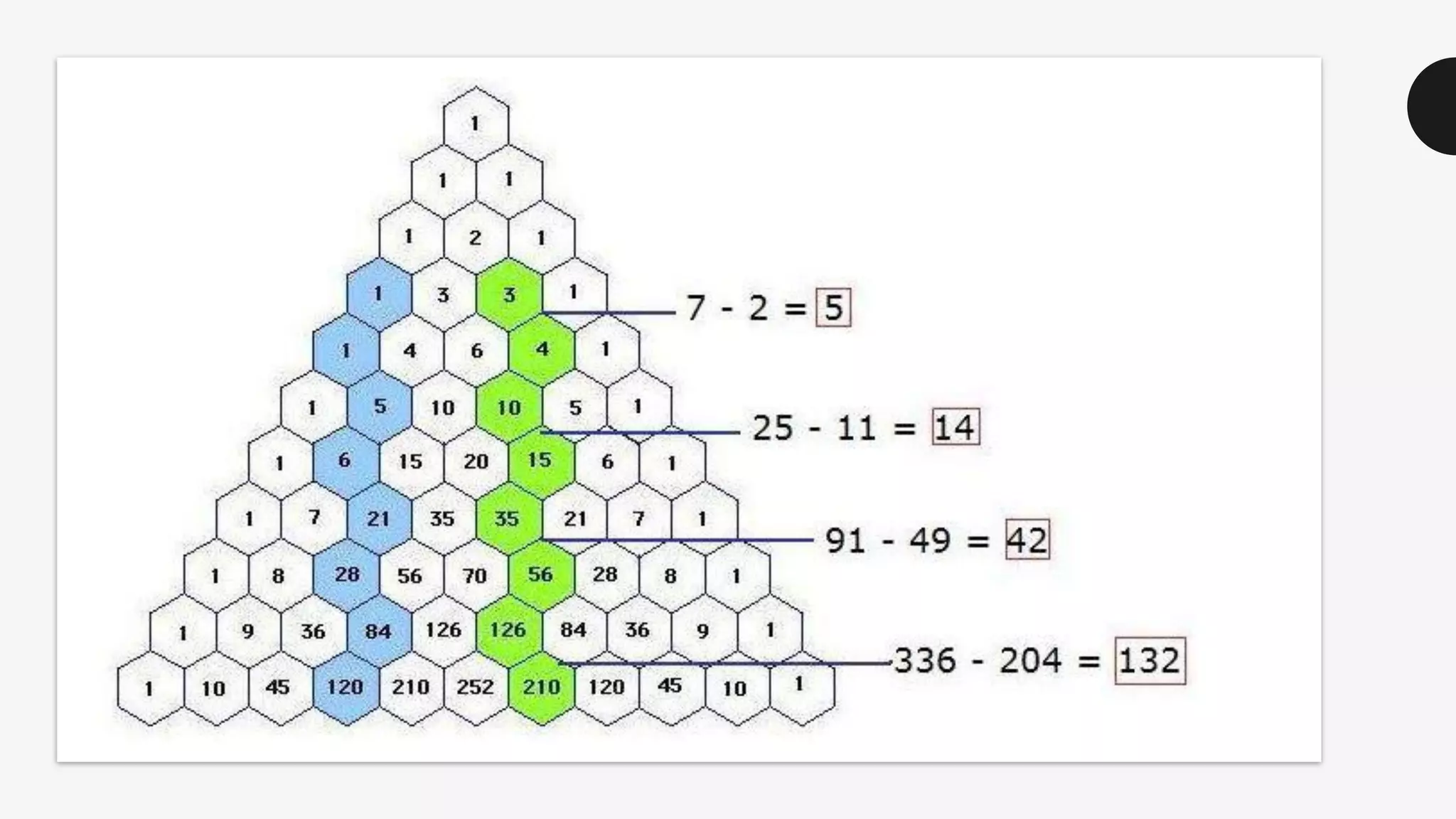
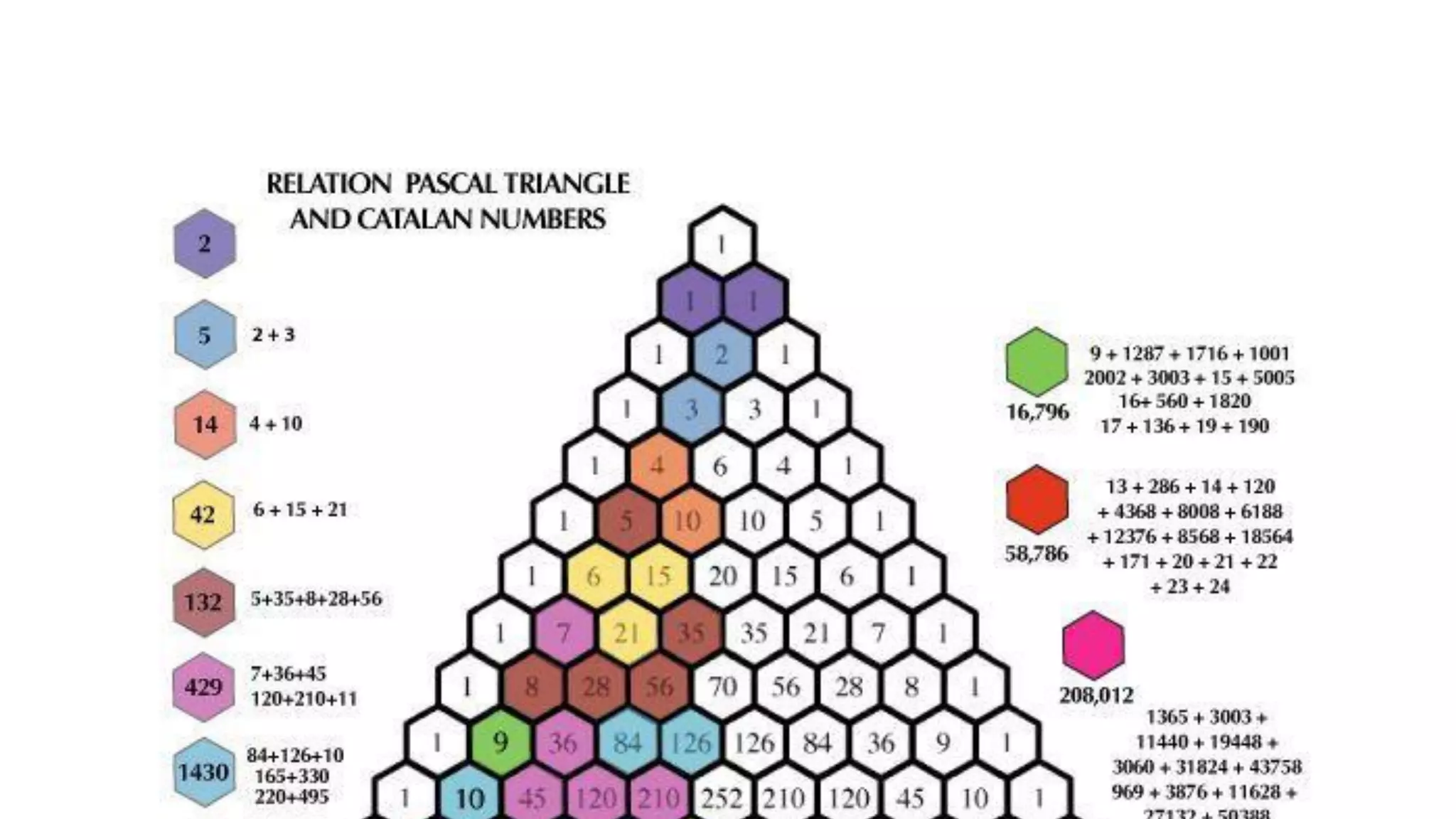
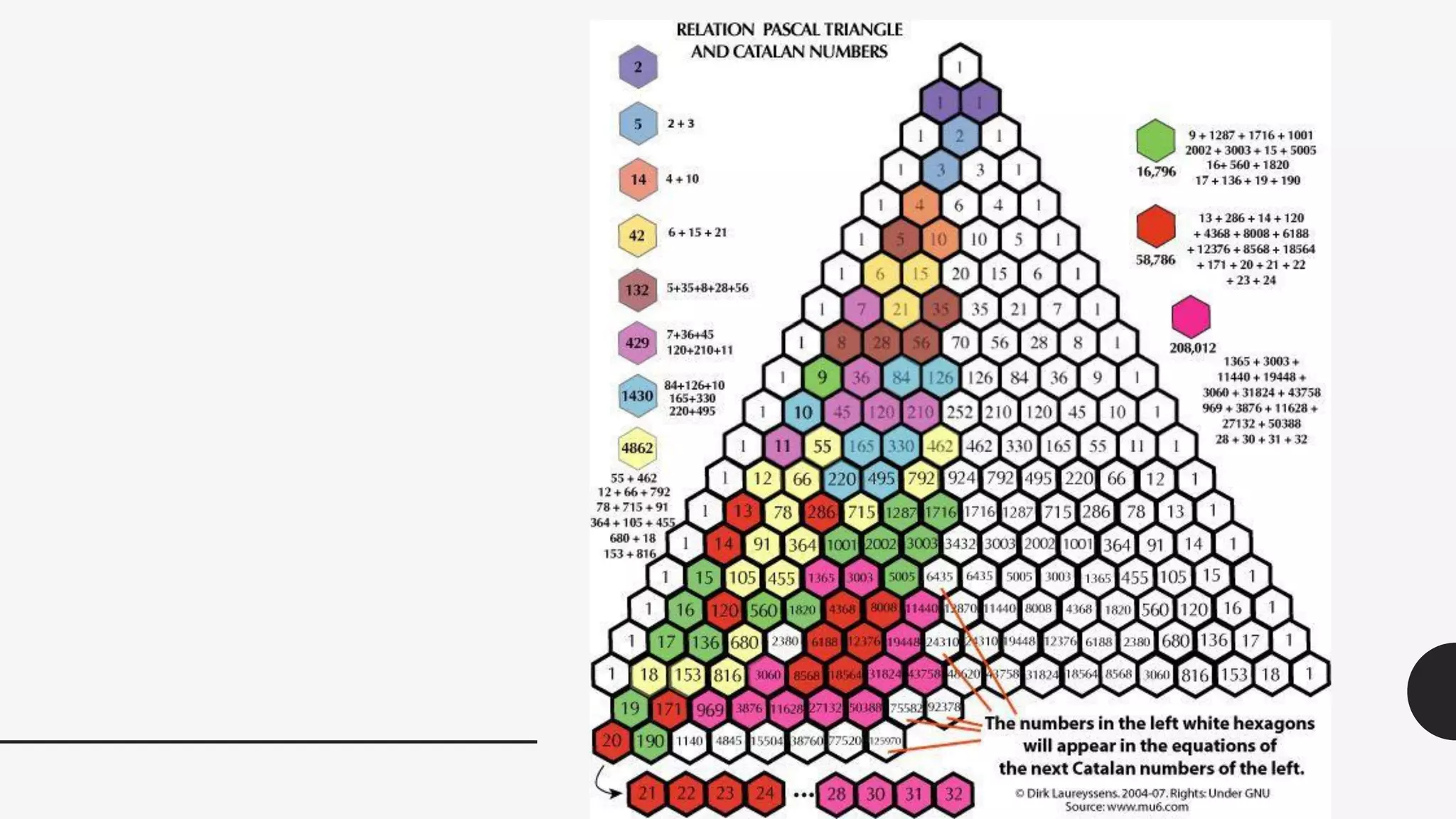
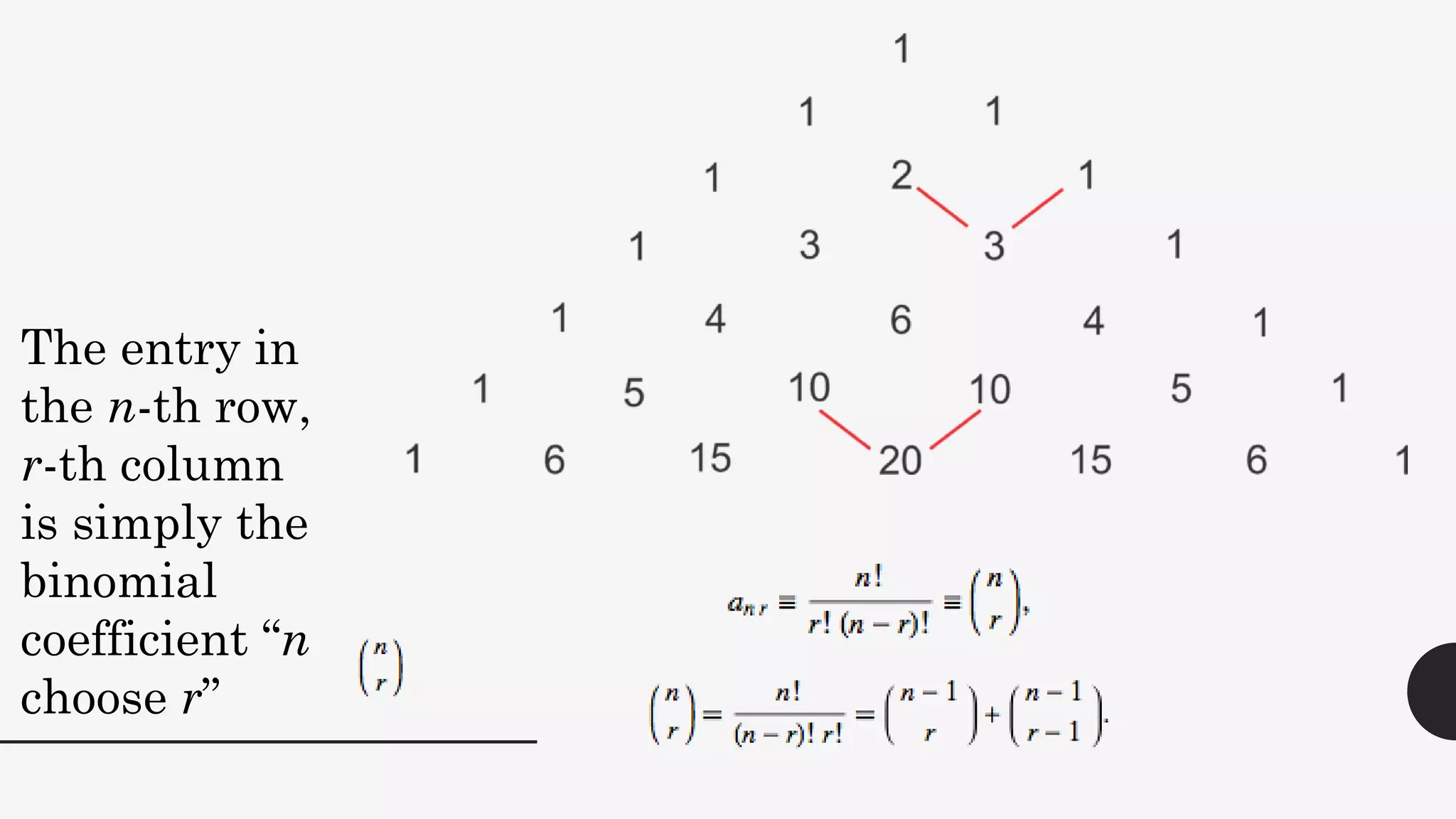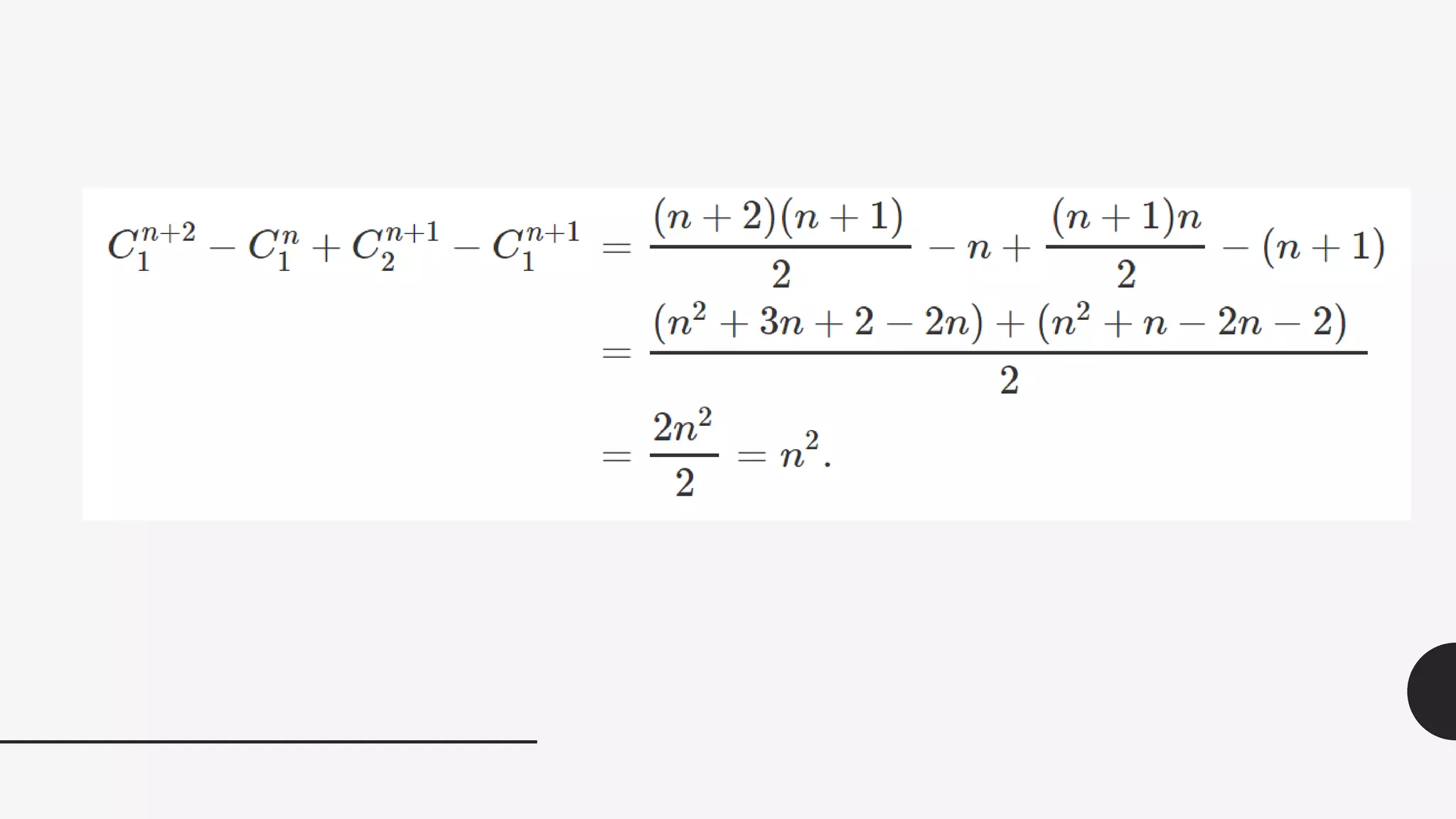This document discusses the life and mathematical contributions of Blaise Pascal. It describes how Pascal discovered important theorems in geometry and probability at a young age. It also explains how Pascal made contributions to philosophy, literature, physics, and the development of early calculating machines. Additionally, the document discusses the history of Pascal's Triangle and some of its key properties, such as binomial coefficients and relationships between row sums.

1. PASCAL’S
TRIANGLE —
BLAISE-ING A
TRAIL OF
MATHEMATICS
EddieTchertchian
Los Angeles Pierce College
AMATYC 2018 – Orlando, FL

2. “All of men’s miseries
derive from not being
able to sit quietly in a
room alone.”
• Born June 19, 1623 in Clermont-
Ferrand, Auvergne, France to
father Etienne Pascal & mother
Antoinette Begon
• Lost mother at the age of 3 –
family relocated to Paris five
years later

3. “Do you wish people to
think well of you? Don’t
speak well of yourself.”
• At age 16 – Pascal’s theorem:
If six arbitrary points are chosen on a
conic (which may be an ellipse,
parabola or hyperbola in an
appropriate affine plane) and joined by
line segments in any order to form a
hexagon, then the three pairs of
opposite sides of the hexagon
(extended if necessary) meet at three
points which lie on a straight line,
called the Pascal line of the hexagon.

4. “I would prefer an intelligent hell to
a stupid paradise.”
• When Etienne became
the king’s commissioner
of taxes in the city of
Rouen, Pascal tried to
aid his father in doing
many computations by
constructing the world’s
first mechanical
calculator, the
“Pascaline.”

5. “To make light of philosophy is to be
a true philosopher.”
• Pascal’s contributions to mathematics
were numerous, as were his contributions
outside of mathematics:
– Philosophy (of mathematics – axiomatic
method; formalism based on Descarte’s work)
– Literature & religion (The Pensées –
“Thoughts”)
– Physical sciences (pressure – Pascal’s principle)
– Probability theory/gambling (primitive form of
roulette wheel)

6. “You always admire what you
really don’t understand.”
• Pascal’s triangle & binomial coefficients were
studied by Pascal in 1653, but had been
described and well-known centuries before
that around the world:
– Indian studies of combinatorics & the numbers of
the triangle date back to Pingala (2nd century BC)
– Iran: Al-Karaji wrote a now lost book which
contained the first description of Pascal’s triangle;
repeated later by Omar Khayyam (1048-1131) –
Khayyam’s triangle
– China: Jia Xian (1010-1070);Yang Hui (1238-1298)
presented the triangle – Yang Hui’s triangle

7. “It is man's natural
sickness to believe
that he possesses the
truth.”
– Germany: Petrus
Apianus – full triangle
published (1527)
– Italy: Tartaglia’s
triangle (1556 – first
six rows); Cardano
published the triangle
& additive and
multiplicative rules for
constructing it. (1570)

8. The entry in
the n-th row,
r-th column
is simply the
binomial
coefficient “n
choose r”

18. 𝟏 + 𝟔 + 𝟐𝟏 + 𝟓𝟔 = 𝟖𝟒
𝟏 + 𝟕 + 𝟐𝟖 + 𝟖𝟒 + 𝟐𝟏𝟎 + 𝟒𝟔𝟐 + 𝟗𝟐𝟒 = 𝟏𝟕𝟏𝟔
𝟏 + 𝟏𝟐 = 𝟏𝟑

19. 𝑛 + 1
𝑚
=
𝑛
𝑚
+
𝑛 − 1
𝑚 − 1
+ ⋯ +
𝑛 − 𝑚
0
𝑚 + 𝑟 + 1
𝑚
=
𝑚 + 𝑟
𝑚
+
𝑚 + 𝑟 − 1
𝑚 − 1
+ ⋯ +
𝑟
0

22. If the 1st element in
a row is a prime
number (remember,
the 0th element of
every row is 1), all
the numbers in
that row (excluding
the 1's) are
divisible by it. For
example, in row 7
(1 7 21 35 35 21 7
1) 7, 21, and 35 are
all divisible by 7.

23. The sum of the squares of the
elements of row n equals the
middle element of row 2n. For
example,
12 + 42 + 62 + 42 + 12 = 70.
In general form:
෍
𝑘=0
𝑛
𝑛
𝑘
2
=
2𝑛
𝑛
Row 4
Row 8 = 2 x 4

24. Sum of the first k rows is the
Mersenne number
2 𝑘 − 1

26. • There are infinitely many numbers that occur at least six times in Pascal’s (whole)
triangle, namely the solutions to:
𝑟 =
𝑛
𝑚 − 1
=
𝑛 − 1
𝑚
given by
𝑚 = 𝐹2𝑘 −1 𝐹2𝑘
𝑛 = 𝐹2𝑘 𝐹2𝑘+1
where 𝐹𝑖 is the 𝑖-th Fibonacci number.
• The numbers that occur five or more times in Pascal’s triangle are 1; 120; 210;
1540; 3003; 7140; 11628; 24310; and the number
61,218,182,743,304,701,891,431,482,520
with no others up to 33 ⋅ 1016

29. Using Nilakantha’s infinite series
for 𝜋

36. “The last thing
one discovers
in composing a
work is what to
put first.”
• Thanks to:
– A Piece of the Mountain:The Story of Blaise Pascal
(Joyce McPherson; Greenleaf press; 1995)
– Pascal’sTriangle: A Study in Combinations (Jason
VanBilliard; CreateSpace Publishing; 2014)
– Blaise Pascal: Reasons of the Heart (Marvin O’Connell;
Wm. B. Eerdmans Publishing Co; 1997)
– http://mathworld.wolfram.com/PascalsTriangle.html and
associated links within
– http://www.cut-the-
knot.org/arithmetic/algebra/PiInPascal.shtml
– https://en.wikipedia.org/wiki/Blaise_Pascal
– https://en.wikipedia.org/wiki/Pascal%27s_triangle
– https://www.goodreads.com/author/quotes/10994.Blaise
_Pascal
– https://www.mathsisfun.com/pascals-triangle.html

37. Thank you!
Eddie
Tchertchian
Los Angeles
Pierce
College
• This presentation is available on SLIDESHARE:
tchertea@piercecollege.edu
http://www.slideshare.net/EddieMath