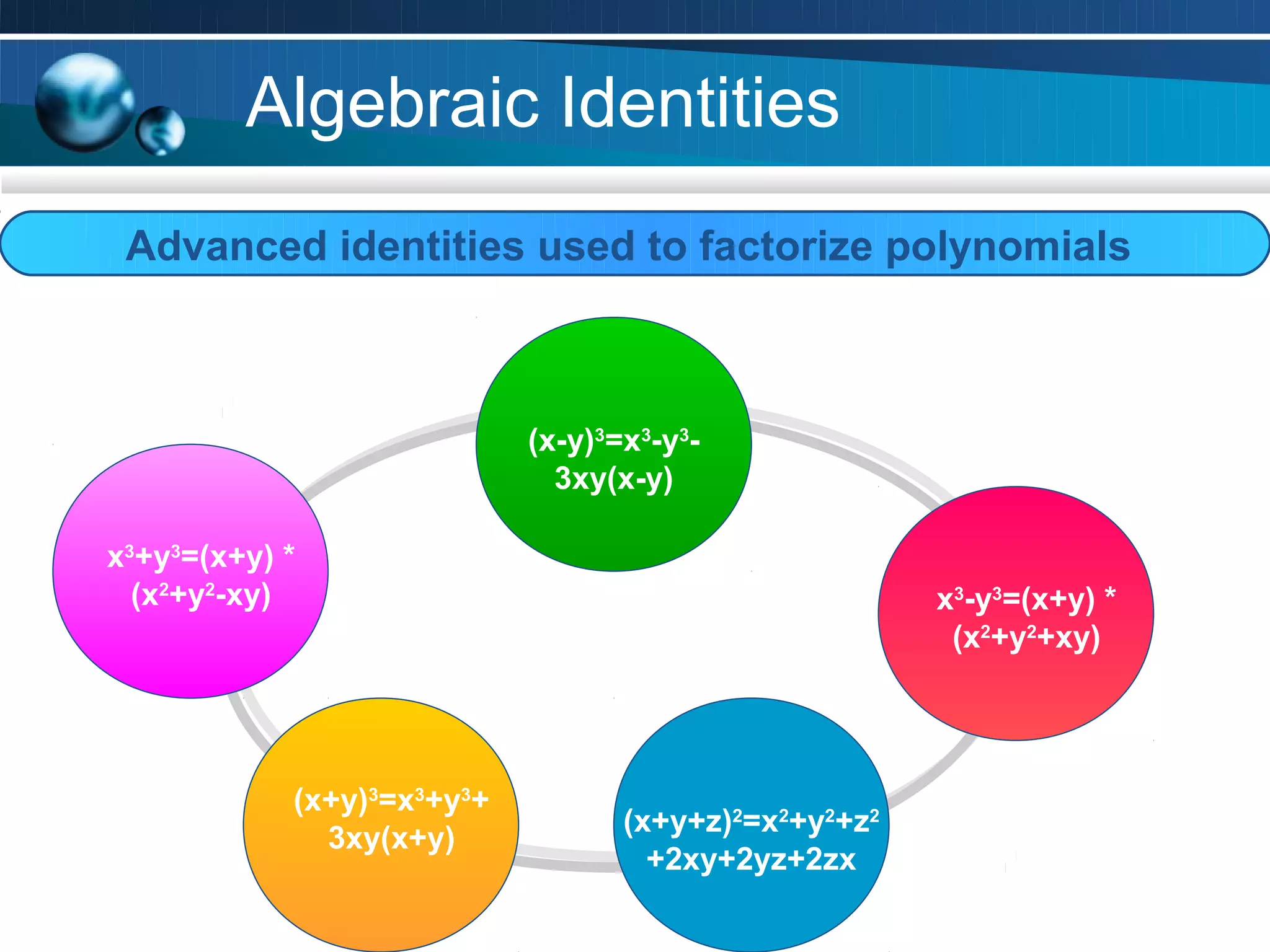
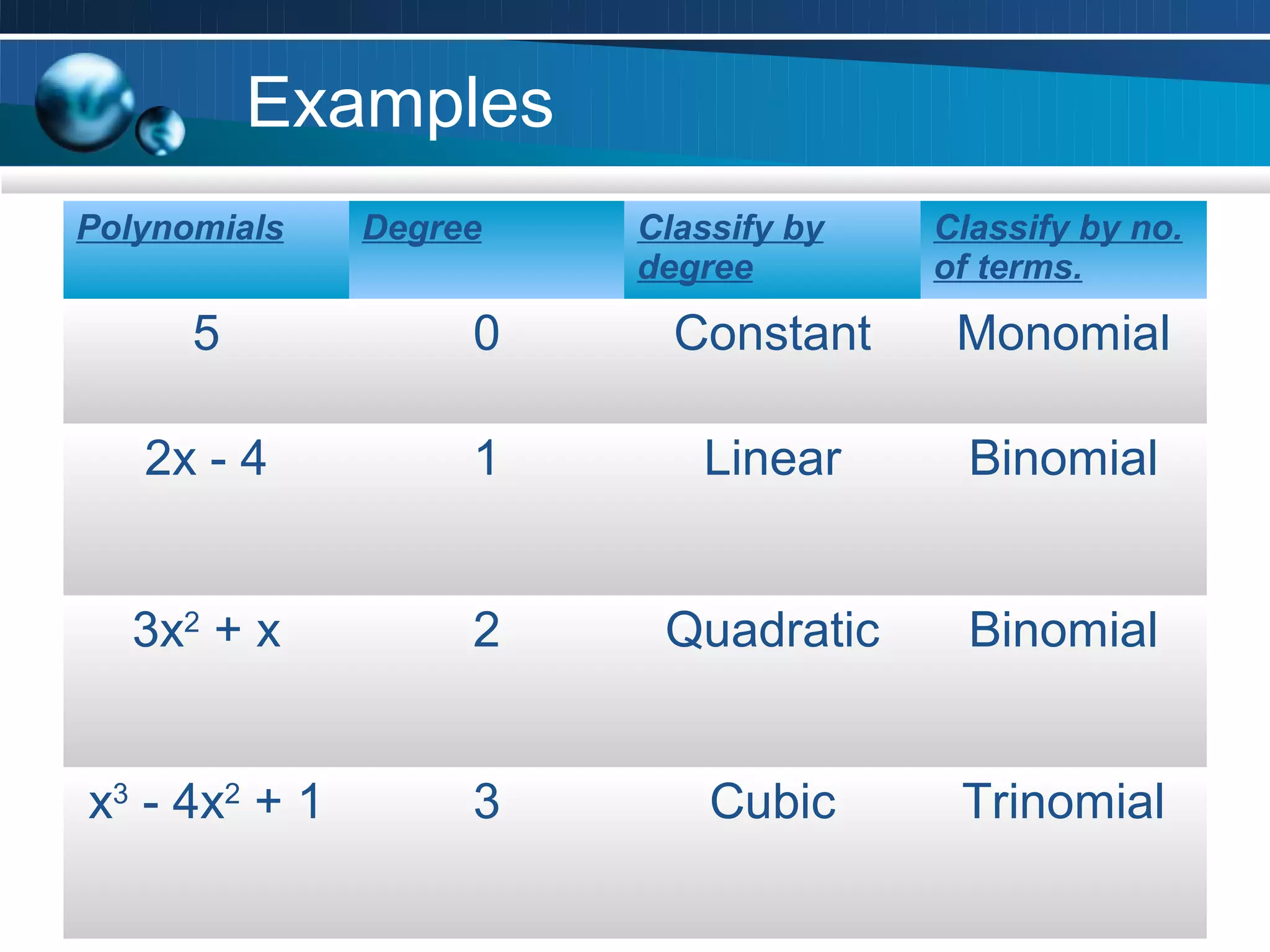
This document is a math project submitted by Aman Yadav of class 9A on polynomials. It covers topics like the definition of polynomials, exponents and terms, degree of polynomials in one and two variables, the remainder theorem, factor theorem, and algebraic identities. It provides examples and questions to explain these concepts. Key points are defined like a polynomial being the sum of monomials, and the degree being the highest power of a variable in a polynomial.

1. Maths Project
• Made By :- Aman Yadav
• Class:-Ix-A
• Roll no. :- 05
• Submitted To:- Mr. Manish Ahuja
(Maths Teacher)
• By The Help oF Mrs.Neetu Sharma
(Computer Teacher)

2. Polynomials

3. Topics Covered
• Polynomials.
• Exponents And Terms.
• Degree Of A Polynomial In One Variable.
• Degree Of A Polynomial In Two Variables.
• Remainder Theorem.
• Factor Theorem.
• Algebric Identities.

4. Polynomials
• A polynomial is a monomial or a sum of monomials.
• Each monomial in a polynomial is a term of the
polynomial.
The number factor of a term is called the coefficient.
The coefficient of the first term in a polynomial is the
lead coefficient.
• A polynomial with two terms is called a binomial.
• A polynomial with three term is called a trinomial.

5. Exponents And Terms.

6. Degree of a Polynomial in one
variable:-
Degree of a Polynomial in one variable. What
is degree of the following binomial? The
answer is 2. 5x2 + 3 is a polynomial in x of
degree 2. In case of a polynomial in one
variable, the highest power of the variable is
called the degree of polynomial .

7. Degree of a Polynomial in two
variables.
• What is degree of the following polynomial?
5 x y − 7 x + 3 xy + 9 y + 4
2 3 3
• Theanswer is five because if we add 2 and 3 , the answer is five
which is the highest power in the whole polynomial.
E.g.- 3 x y − 5 x + 8 xy + 2 y + 9
3 4 2
is a polynomial in x
and y of degree 7.
In case of polynomials on more than one variable, the sum of
powers of the variables in each term is taken up and the highest
sum so obtained is called the degree of polynomial.

8. Polynomials in one variable
The degree of a polynomial in one variable is the largest
exponent of that variable.
2 A constant has no variable. It is a 0 degree polynomial.
4x +1 This is a 1st degree polynomial. 1st degree polynomials
are linear.
5 x + 2 x − 14
2 This is a 2nd degree polynomial. 2nd
degree polynomials are quadratic.
3 x − 18 This is a 3rd are cubic.
3
polynomials
degree polynomial. 3rd degree

9. Examples
Polynomials Degree Classify by Classify by no.
degree of terms.
Text
5 0 Constant Monomial
Txt
2x - 4 1 Linear Binomial
Text
3x2 + x 2 Quadratic Binomial
Text
Text
x - 4x + 1
3 2
3 Cubic Trinomial

10. Remainder Theorem
Let f(x) be a polynomial of degree n > 1 and let a be any real number.
When f(x) is divided by (x-a) , then the remainder is f(a).
TEXT TEXT TEXT TEXT
PROOF Suppose when f(x) is divided by (x-a), the quotient is g(x) and the remainder
is r(x).
Then, degree r(x) < degree (x-a)
degree r(x) < 1 [ therefore, degree (x-a)=1]
degree r(x) = 0
r(x) is constant, equal to r (say)
Thus, when f(x) is divided by (x-a), then the quotient is g9x) and the remainder is r.
Therefore, f(x) = (x-a)*g(x) + r (i)
Putting x=a in (i), we get r = f(a)
Thus, when f(x) is divided by (x-a), then the remainder is f(a).

11. Questions on Remainder Theorem
Q.) Find the remainder when the polynomial
f(x) = x4 + 2x3 – 3x2 + x – 1 is divided by (x-2).
A.) x-2 = 0 x=2
By remainder theorem, we know that when f(x) is divided by (x-2),
the remainder is x(2).
Now, f(2) = (24 + 2*23 – 3*22 + 2-1)
= (16 + 16 – 12 + 2 – 1) = 21.
Hence, the required remainder is 21.

12. Factor Theorem
Let f(x) be a polynomial of degree n > 1 and let a be
any real number.
(i) If f(a) = 0 then (x-a) is a factor of f(x).
PROOF let f(a) = 0
On dividing f(x) by 9x-a), let g(x) be the quotient. Also,
by remainder theorem, when f(x) is divided by (x-a),
then the remainder is f(a).
therefore f(x) = (x-a)*g(x) + f(a)
f(x) = (x-a)*g(x) [therefore f(a)=0(given]
(x-a) is a factor of f(x).

13. Algebraic Identities
Some common identities used to factorize polynomials
(a+b)2=a2+b2+2ab (a-b)2=a2+b2-2ab a2-b2=(a+b)(a-b) (x+a)(x+b)=x2+(a+b)x+ab

14. Algebraic Identities
Advanced identities used to factorize polynomials
(x-y)3=x3-y3-
3xy(x-y)
x3+y3=(x+y) *
(x2+y2-xy) x3-y3=(x+y) *
(x2+y2+xy)
(x+y)3=x3+y3+
(x+y+z)2=x2+y2+z2
3xy(x+y)
+2xy+2yz+2zx

15. Q/A on Polynomials
Q.1) Show that (x-3) is a factor of polynomial
f(x)=x3+x2-17x+15.
A.1) By factor theorem, (x-3) will be a factor of f(x) if f(3)=0.
Now, f(x)=x3+x2-17x+15
f(3)=(33+32-17*3+15)=(27+9-51+15)=0
(x-3) is a factor of f(x).
Hence, (x-3) is a factor of the given polynomial f(x).

16. Q/A on Polynomials
Q.1) Factorize:
(i) 9x2 – 16y2 (ii)x3-x
A.1)(i) (9x2 – 16y2) = (3x)2 – (4y)2
= (3x + 4y)(3x – 4y)
therefore, (9x2-16y2) = (3x + 4y)(3x – 4y)
(ii) (x3-x) = x(x2-1)
= x(x+1)(x-1)
therefore, (x3-x) = x(x + 1)(x-1)

17. Points to Remember
• A real number ‘a’ is a zero of a polynomial p(x) if p(a)=0. In
this case, a is also called a root of the equation p(x)=0.
• Every linear polynomial in one variable has a unique zero, a
non-zero constant polynomial has no zero, and every real
number is a zero of the zero polynomial.

18. THANK YOU
With Regards:-
Aman Yadav