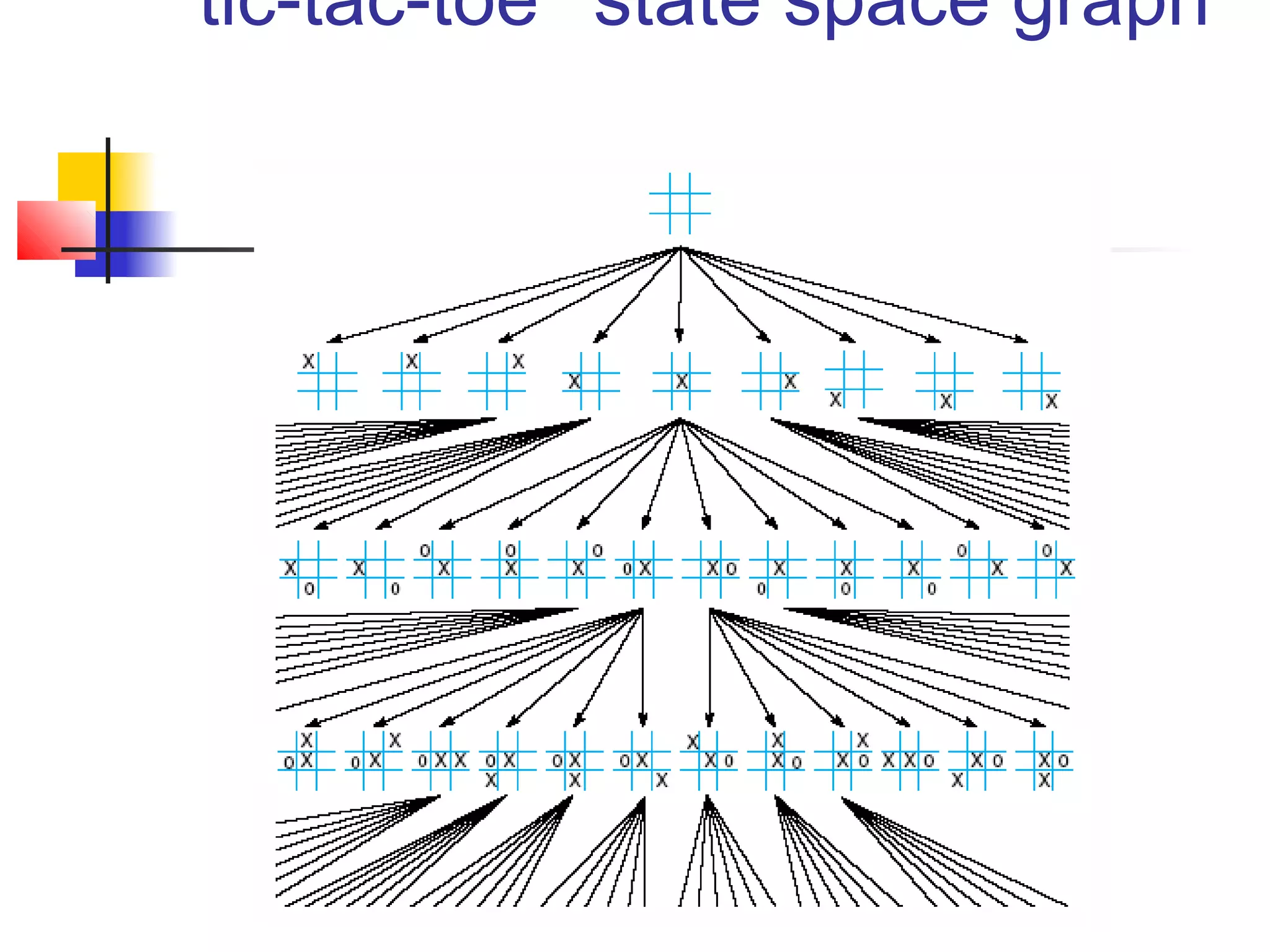
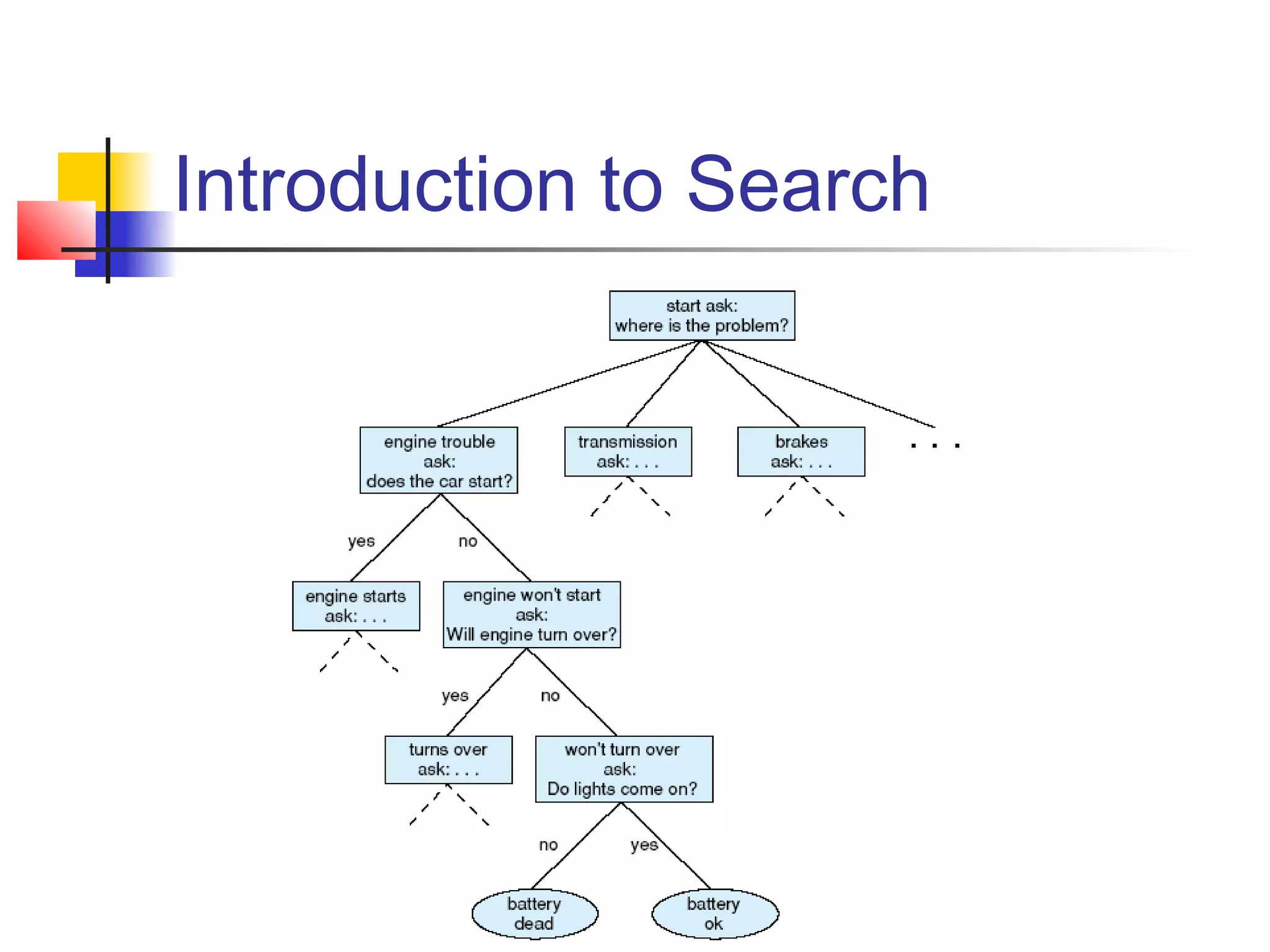
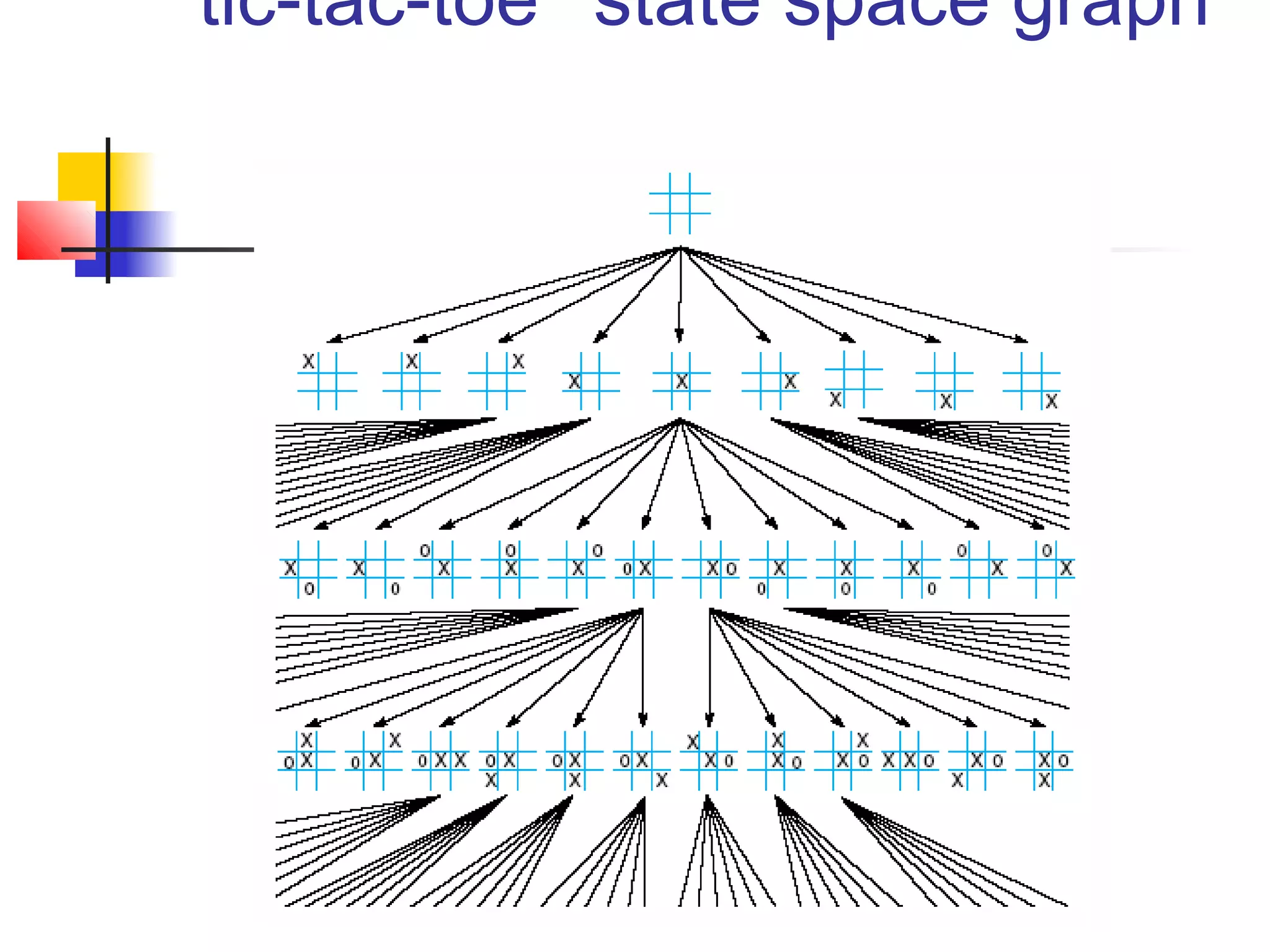
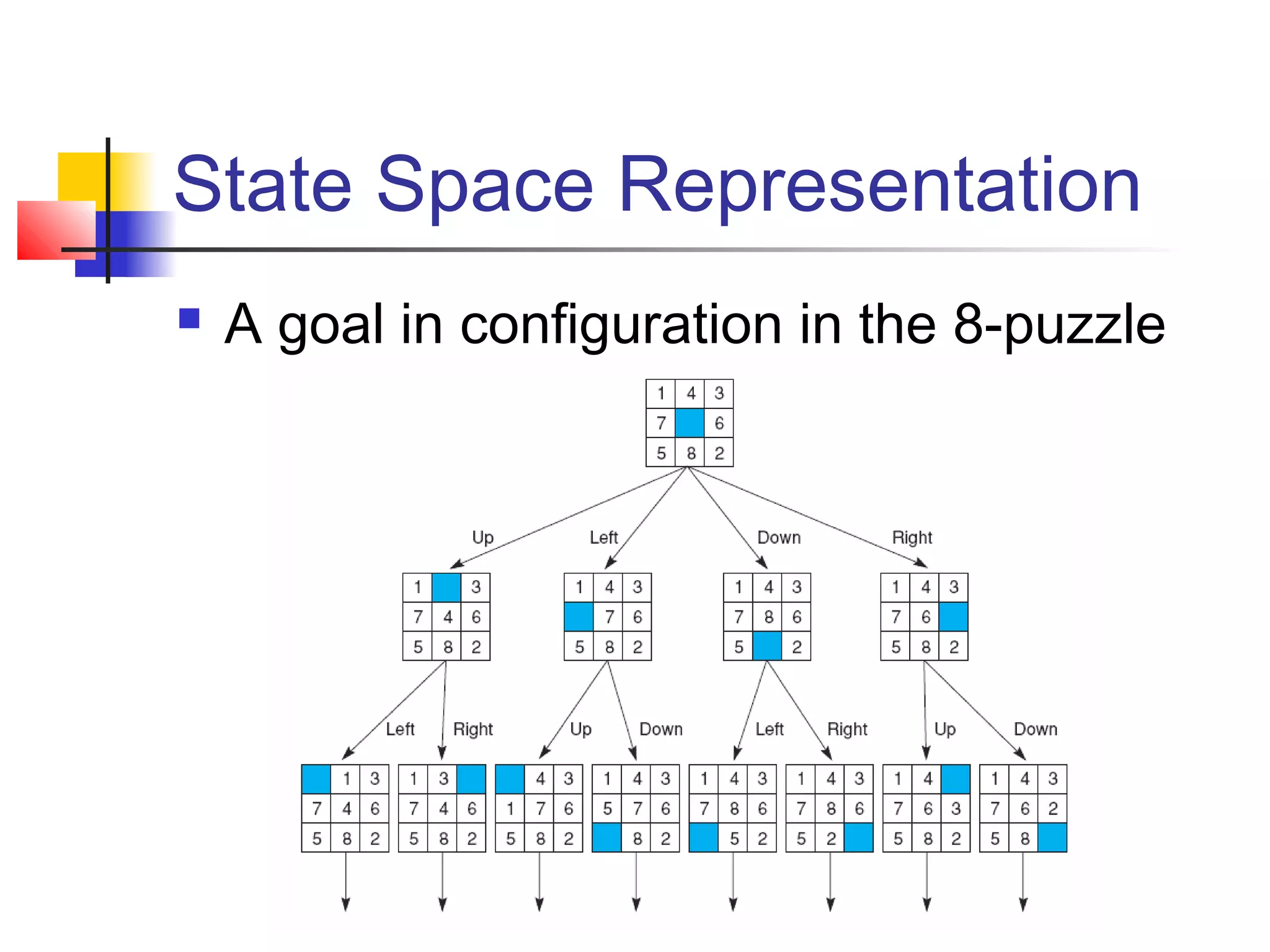
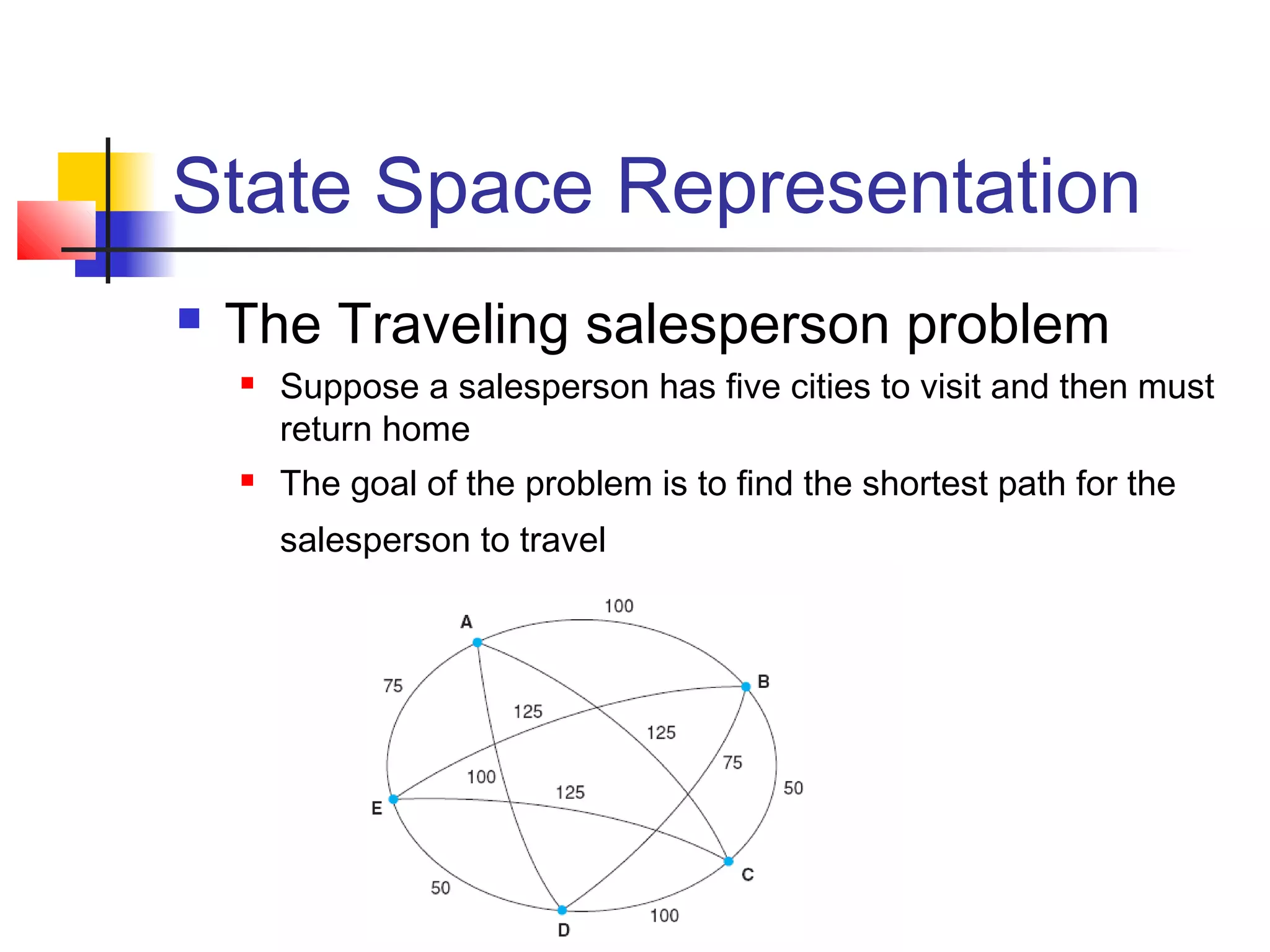
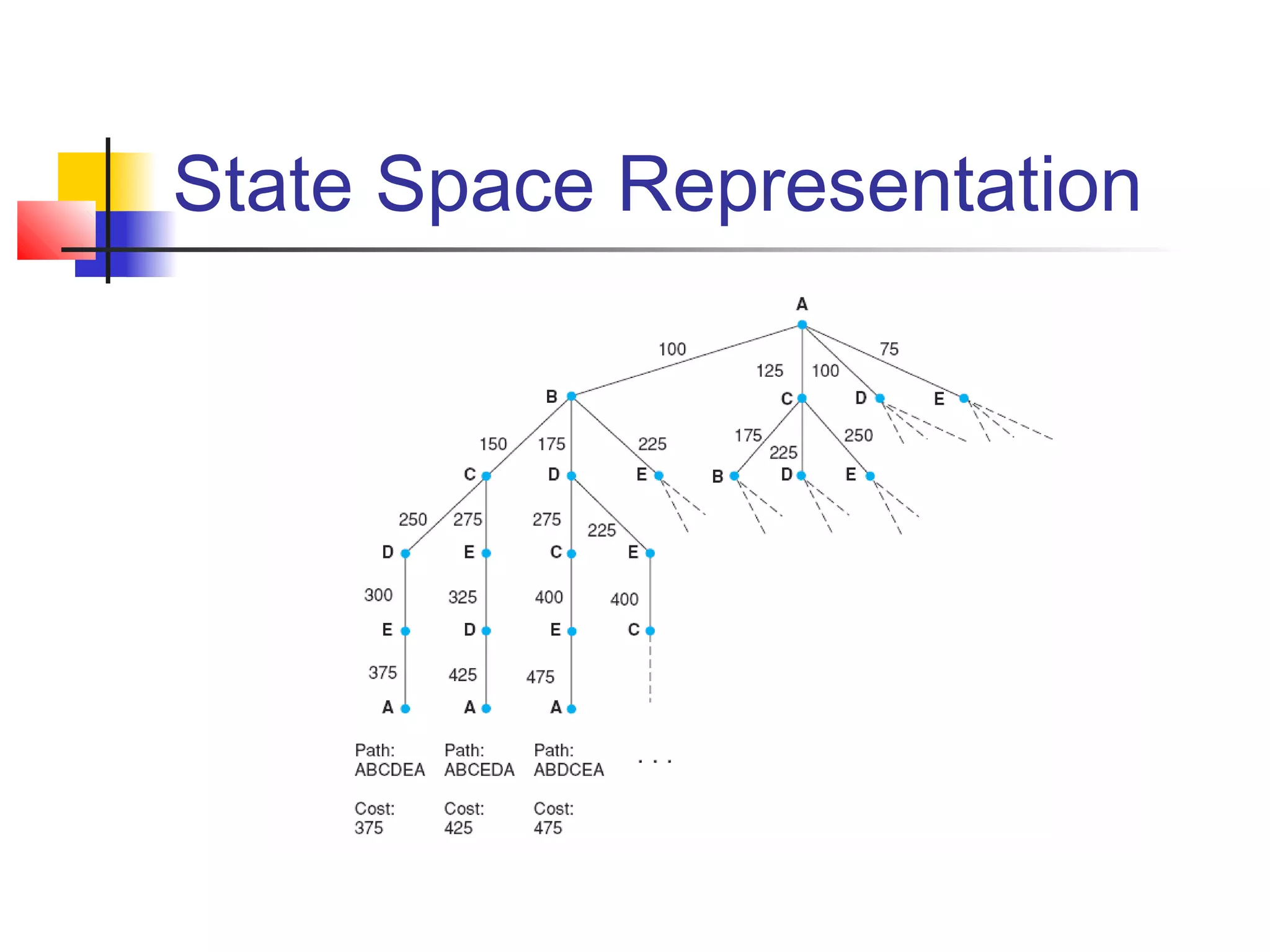
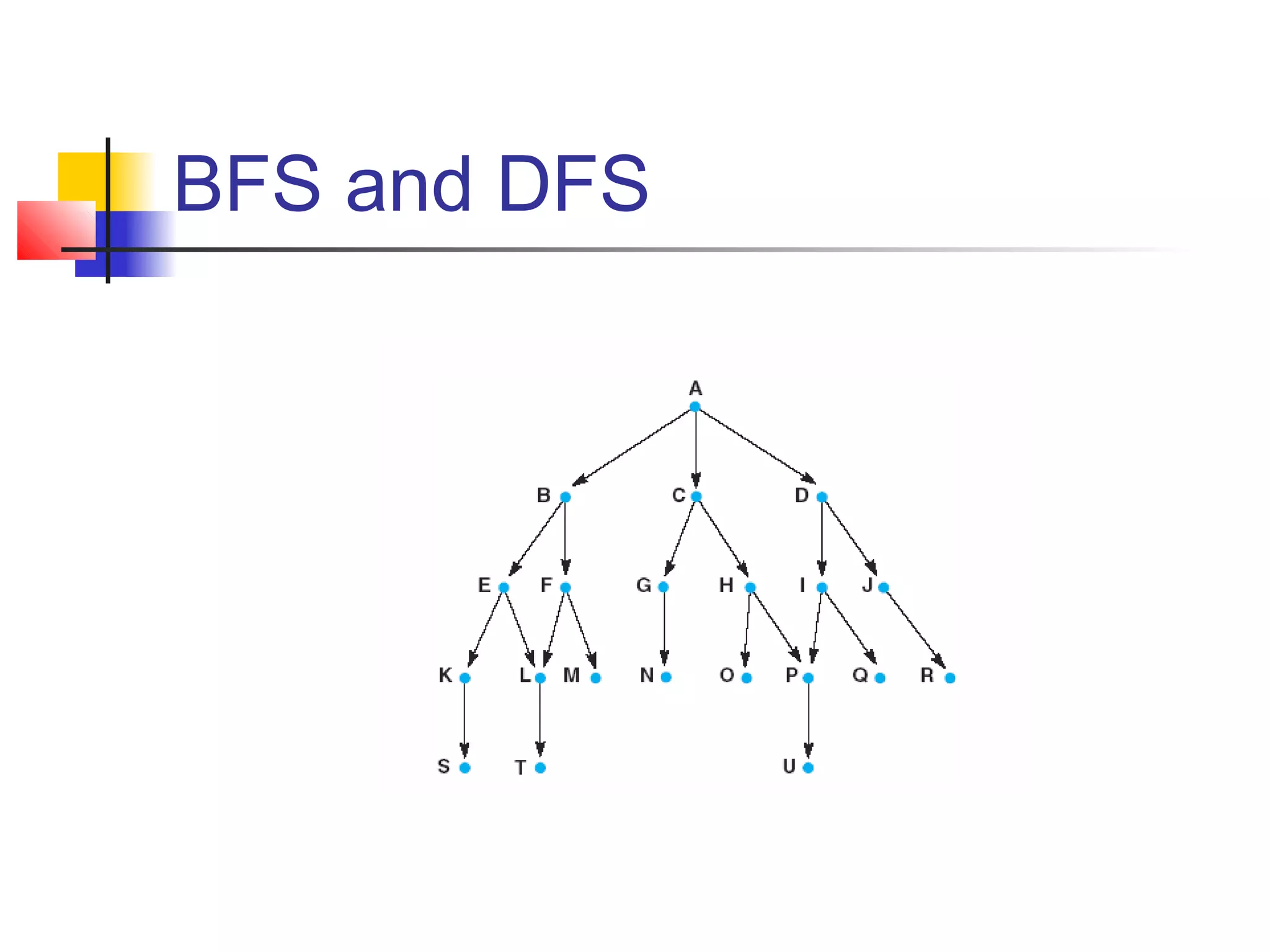
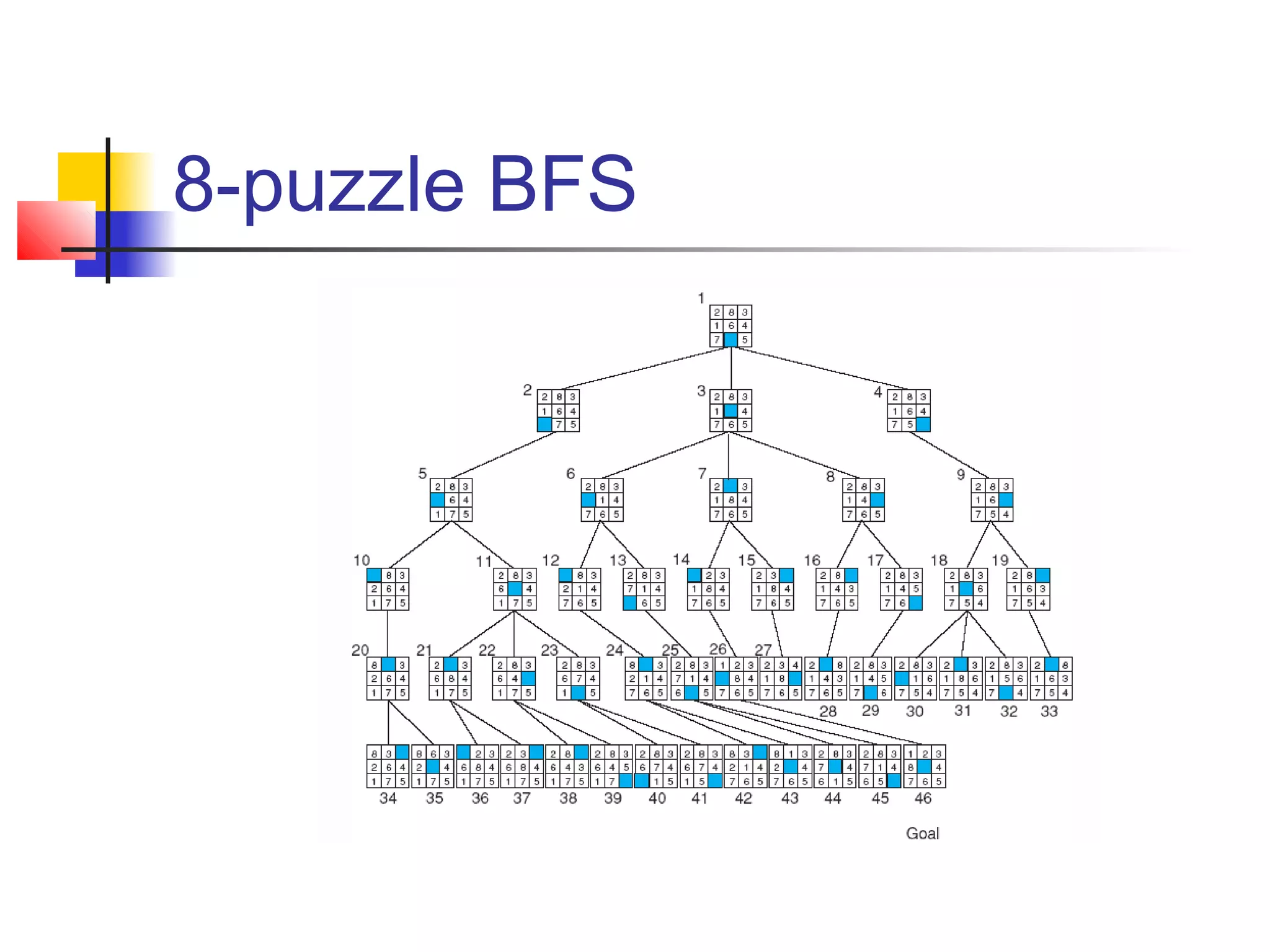
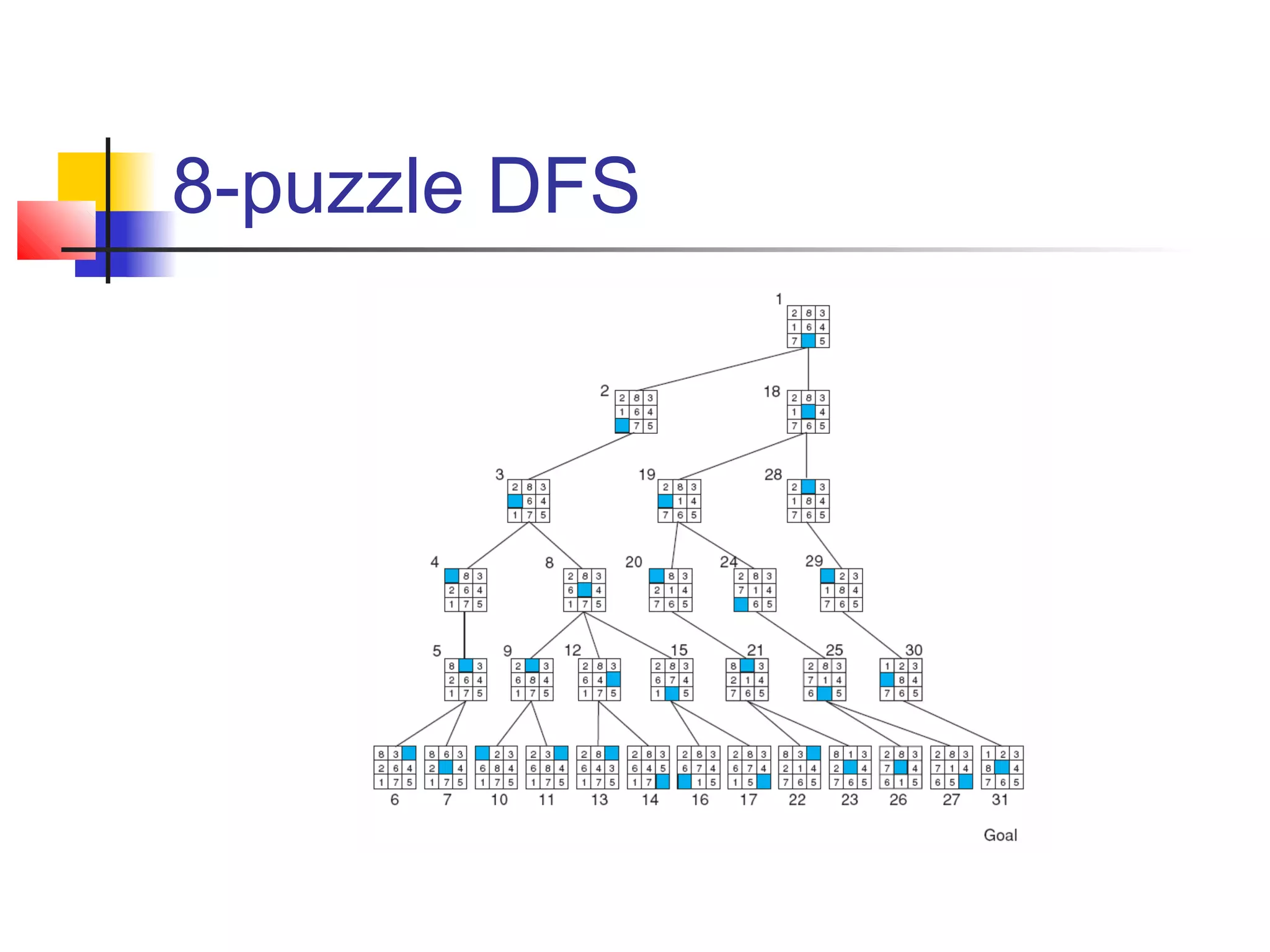
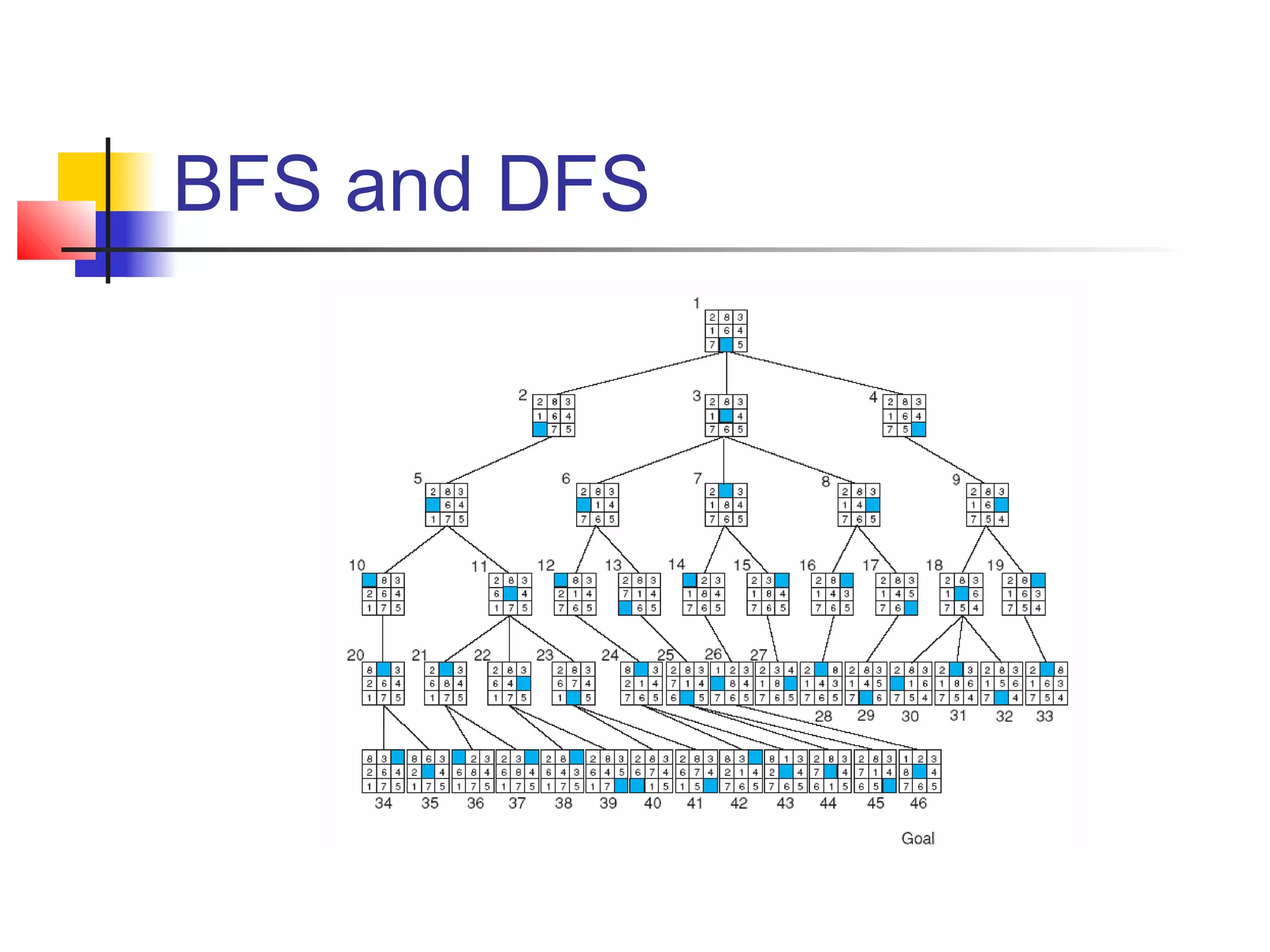
This document summarizes key concepts from a university lecture on artificial intelligence representation and search. It introduces representation as capturing problem features to enable problem solving. Search strategies like depth-first and breadth-first are then discussed, along with their properties and tradeoffs. State space graphs are used to represent problems, with nodes as states and edges as moves. Different problems like tic-tac-toe, the 8-puzzle, and traveling salesperson are provided as examples.

1. Part2 AI as Representation
and Search
Dr. Bernard Chen Ph.D.
University of Central Arkansas
Spring 2011

2. Outline


Intro to Representation and
Search
Ch3 Structures and strategies for state
space search

3. Introduction to Representation


The representation function is to capture
the critical features of a problem and make
that information accessible to a problem
solving procedure
Expressiveness (the result of the feature
abstracted) and efficiency (the
computational complexity) are major
dimensions for evaluating knowledge
representation

4. Introduction to Representation



The computer representation of floating-point
numbers illustrate these trade-off
To be precise, real number require an infinite
string of digits to be fully described.
This cannot be accomplished on a finite
device such as computer

5. Introduction to Representation

6. Introduction to Representation


The array is another representation
common in computer science
For many problems, it is more natural
and efficient than the memory
architecture implemented in computer
hardware

7. Introduction to Representation

8. Introduction to Search


Given a representation, the second
component of intelligent problem solving is
search
Human generally consider a number of
alternatives strategies on their way to solve a
problem



Such as chess
Player reviews alternative moves, select the “best”
move
A player can also consider a short term gain

9. Introduction to Search

Consider “tic-tac-toe”




Starting with an empty board,
The first player can place a X on any one
of nine places
Each move yields a different board that will
allow the opponent 8 possible responses
and so on…

10. Introduction to Search



We can represent this collection of possible
moves by regarding each board as a state
in a graph
The link of the graph represent legal move
The resulting structure is a state space
graph

11. “tic-tac-toe” state space graph

12. Introduction to Search

Consider a task of diagnosing a
mechanical fault in an automobile:

13. Introduction to Search

14. Introduction to Search

Human use intelligent search

Human do not do exhaustive search

The rules are known as heuristics,
and they constitute one of the central
topics of AI search

15. Outline


Intro to Representation and Search
Ch3 Structures and strategies for
state space search

16. State Space Representation



In the state space representation of a problem, the
nodes of a graph correspond to partial problem
solution states and the arcs correspond to steps in a
problem solving process
One or more initial states form the root of the graph
The graph also defines one or more goal conditions,
which are solutions to a problem

17. State Space Representation


State space search characterizes
problem solving as the process of
finding a solution path form the start
state to a goal
A goal may describe a state, such as
winning board in tic-tac-toe

18. “tic-tac-toe” state space graph

19. State Space Representation



In the 8-puzzle, 8 different numbered tiles are fitted
into 9 spaces on a grid
One space is left blank so that tiles can be moved
around to form different patterns
The goal is to find a series of moves of tiles into the
blank space that places the board in a goal
configuration:

20. State Space Representation

A goal in configuration in the 8-puzzle

21. State Space Representation

The Traveling salesperson problem


Suppose a salesperson has five cities to visit and then must
return home
The goal of the problem is to find the shortest path for the
salesperson to travel

22. State Space Representation

An instance of the traveling salesperson
problem with some greedy concept

23. State Space Representation

24. State Space Representation


As previous slide suggests, the
complexity of exhaustive search in the
traveling salesperson problem is (N-1)!
It is a NP problem

25. Outline


Strategies for state space search
Depth-First and Breadth-First Search

26. Strategies for state space
search

A state may be searched in two
directions:


From the given data of a problem instance
toward a foal or
From a goal to the data

27. Strategies for state space
search


In data driven search, also called forward
chaining, the problem solver begins with the given
facts of the problem and set of legal moves for
changing state
This process continues until (we hope!!) it generates
a path that satisfies the goal condition

28. Strategies for state space
search




An alternative approach (Goal Driven) is start with the goal
that we want to solve
See what rules can generate this goal and determine what
conditions must be true to use them
These conditions become the new goals
Working backward through successive subgoals until (we hope
again!) it work back to

29. Strategies for state space
search

For example:
Consider the problem of confirming or
denying the statement “I am a
descendant of Thomas Jefferson”

Some facts:


He was born about 250 years ago
Assume 25 years per generation

30. Strategies for state space
search



As each person has 2 parents, if we search back
(goal driven) starting from “I”, the search space
would be 2^10
If we assume an average of only 3 children per
family, the search space for search forward (data
driven) would be 3^10
Therefore, the decision to choose between data- and
goal- driven search is based on the structure of the
problem

31. Outline


Strategies for state space search
Depth-First and Breadth-First
Search

32. BFS and DFS


In addition to specifying a search direction
(data-driven or goal-driven), a search
algorithm must determine the order in which
states are examined in the graph
Two possibilities:


Depth-first search
Breadth-first search

33. BFS and DFS


In DFS, when a state is examined, all of
its children and their descendants are
examined before any of its siblings
Breadth-first search explores the space
in a level-by-level fashion

34. BFS and DFS

35. BFS and DFS


DFS results:
ABEKSLTFMCGNHOPUDIQJR
BFS results:
ABCDEFGHIJKLMNOPQRSTU

36. 8-puzzle BFS

37. 8-puzzle DFS

38. BFS and DFS

Properties of BFS



Because it always examines all nodes at
level n before proceeding to level n+1, BFS
always finds the shortest path to a goal
In a problem have a simple solution, the
solution will be found
Unfortunately, if the states have a high
average number of children, it may use all
the memory before it find a solution

39. BFS and DFS

Properties of DFS


If it is known that the solution path will be
long, DFS will not spend time searching a
large number of “shallow” states in the
graph
However, DFS may “lost” deep in a graph,
missing short paths to a goal, or even
stuck in an infinite loop

40. BFS and DFS


A nice compromise on these trade-offs
is to use a depth bound on DFS
New slide shows a DFS with a depth
bound of 5

41. BFS and DFS

42. BFS and DFS


DFS with iterative deepening performs
a DFS search of the space with a depth
bound of 1,
If it fails to find a goal, it performs
another DFS with depth bound of 2

43. BFS and DFS



Unfortunately, all the search strategies
discussed in this chapter may be shown to
have worst-case exponential time complexity
This is true for all uniformed search
algorithms
Any other search algorithms???