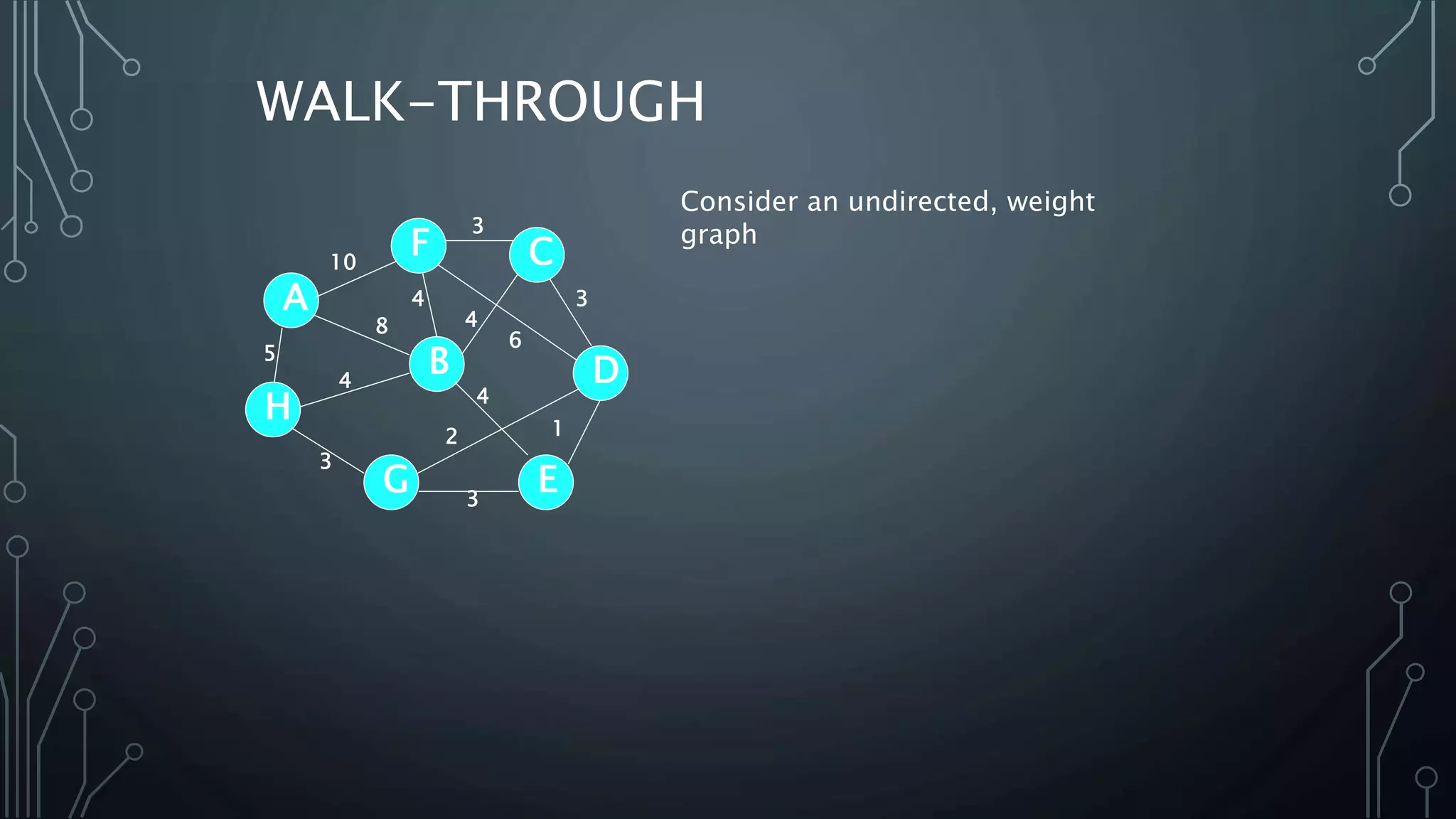
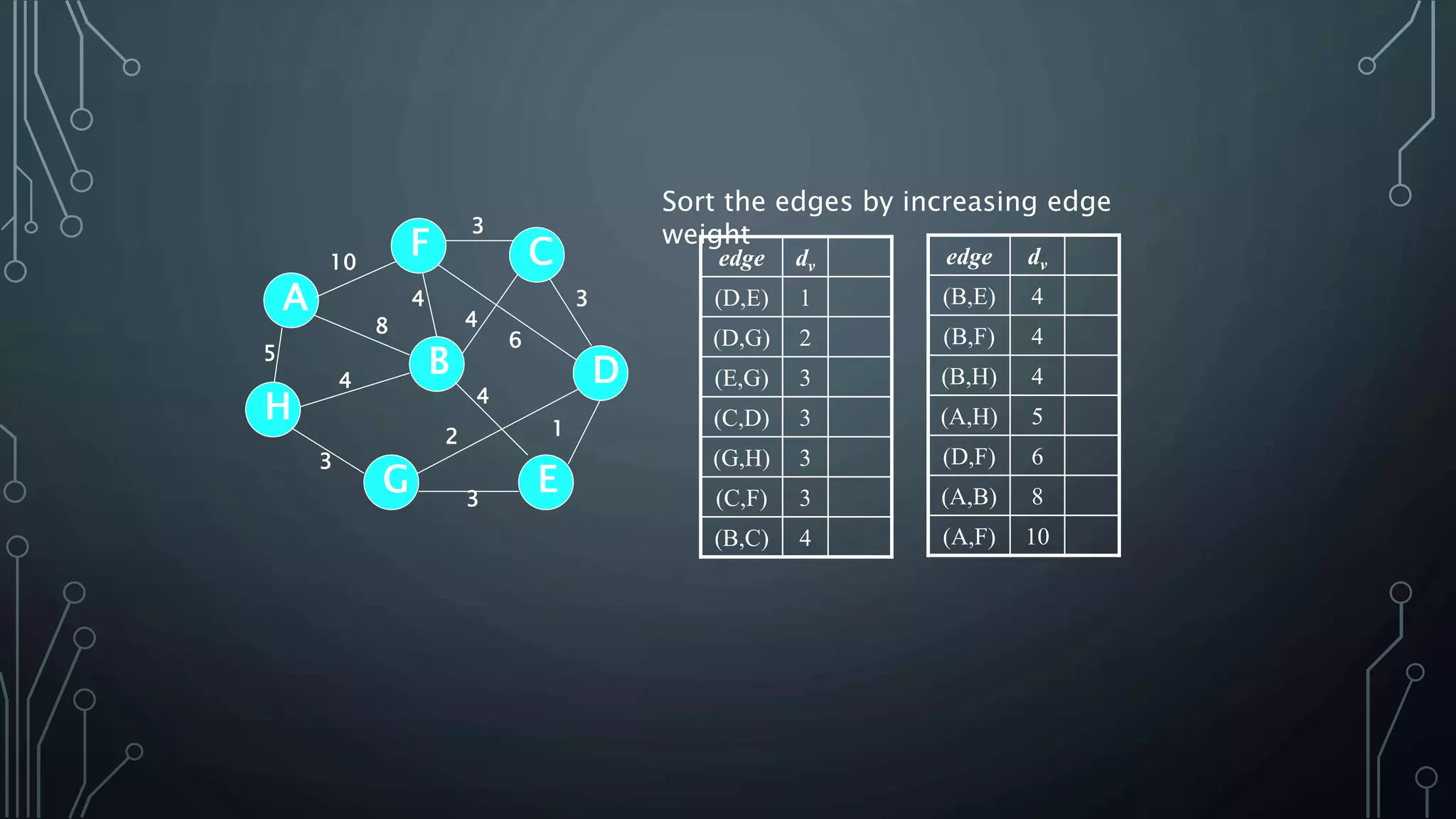
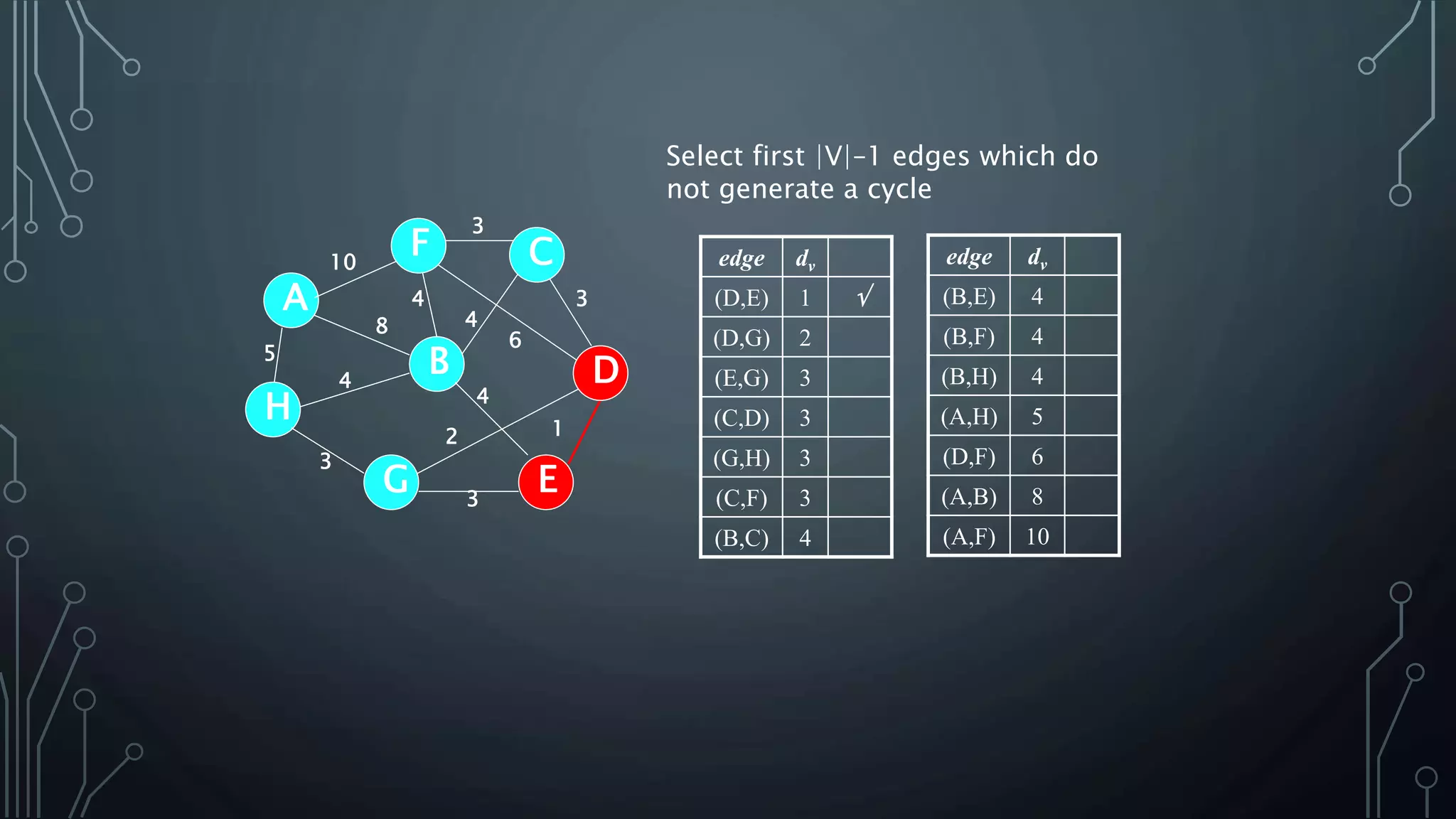
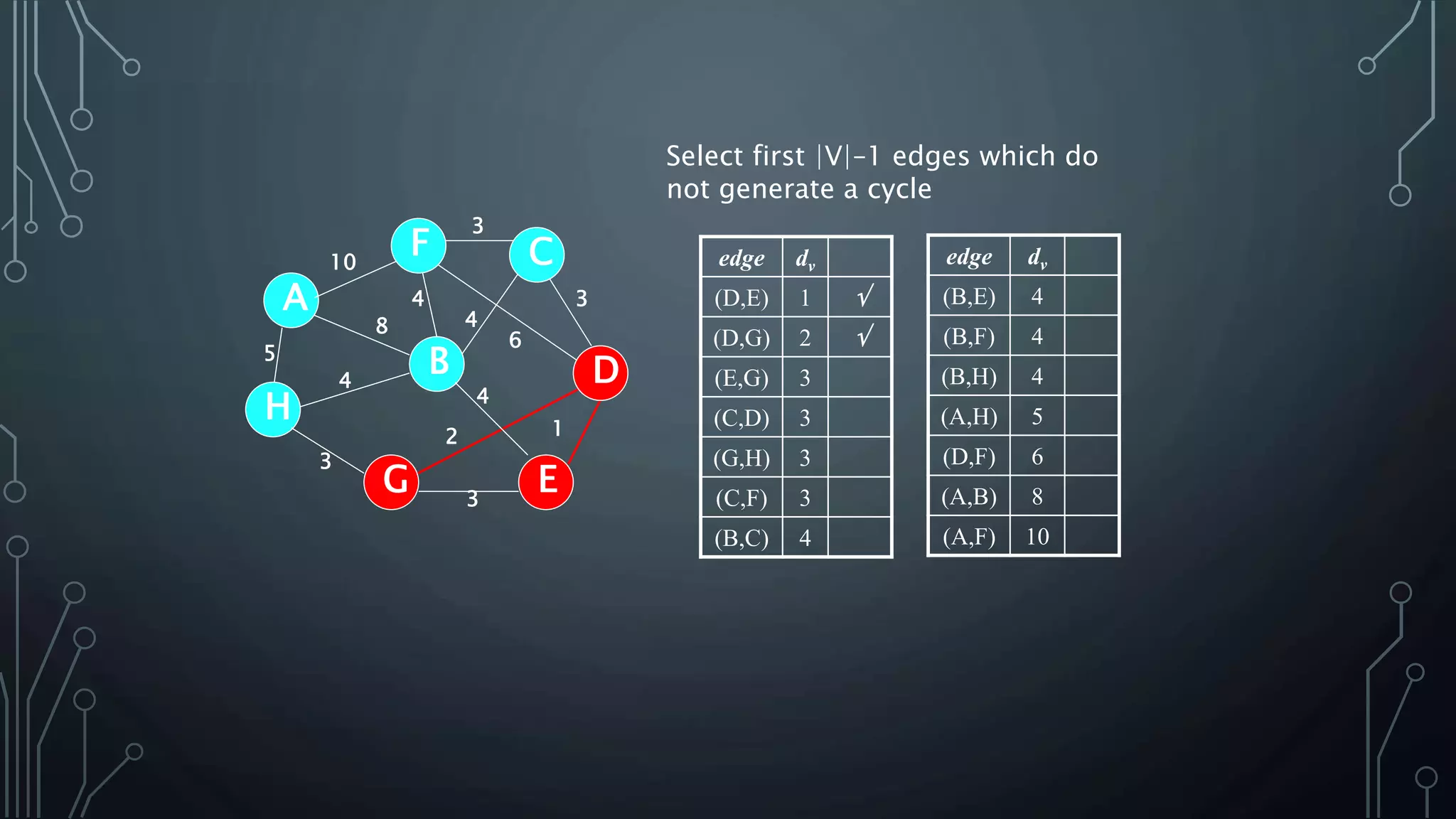
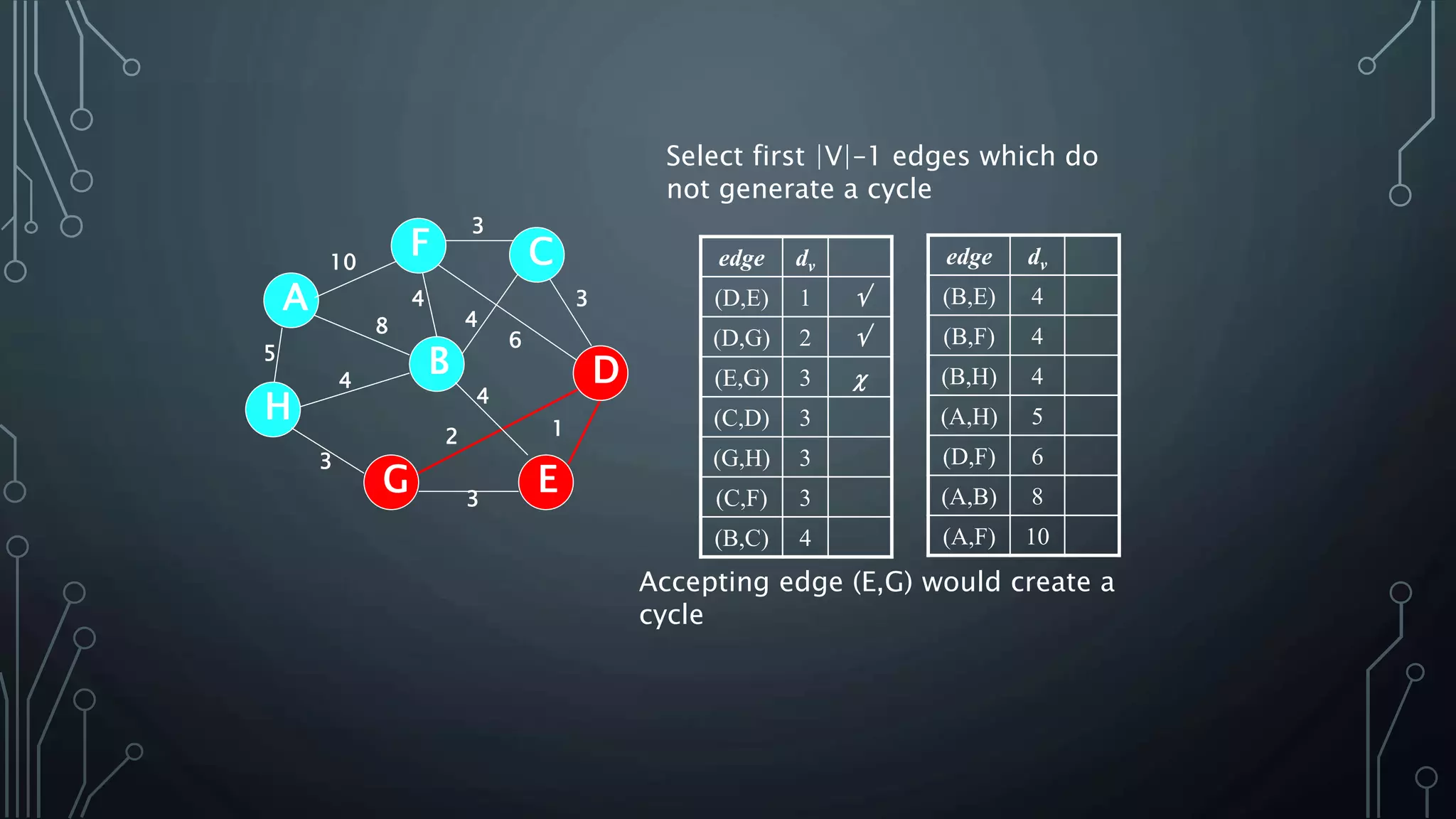
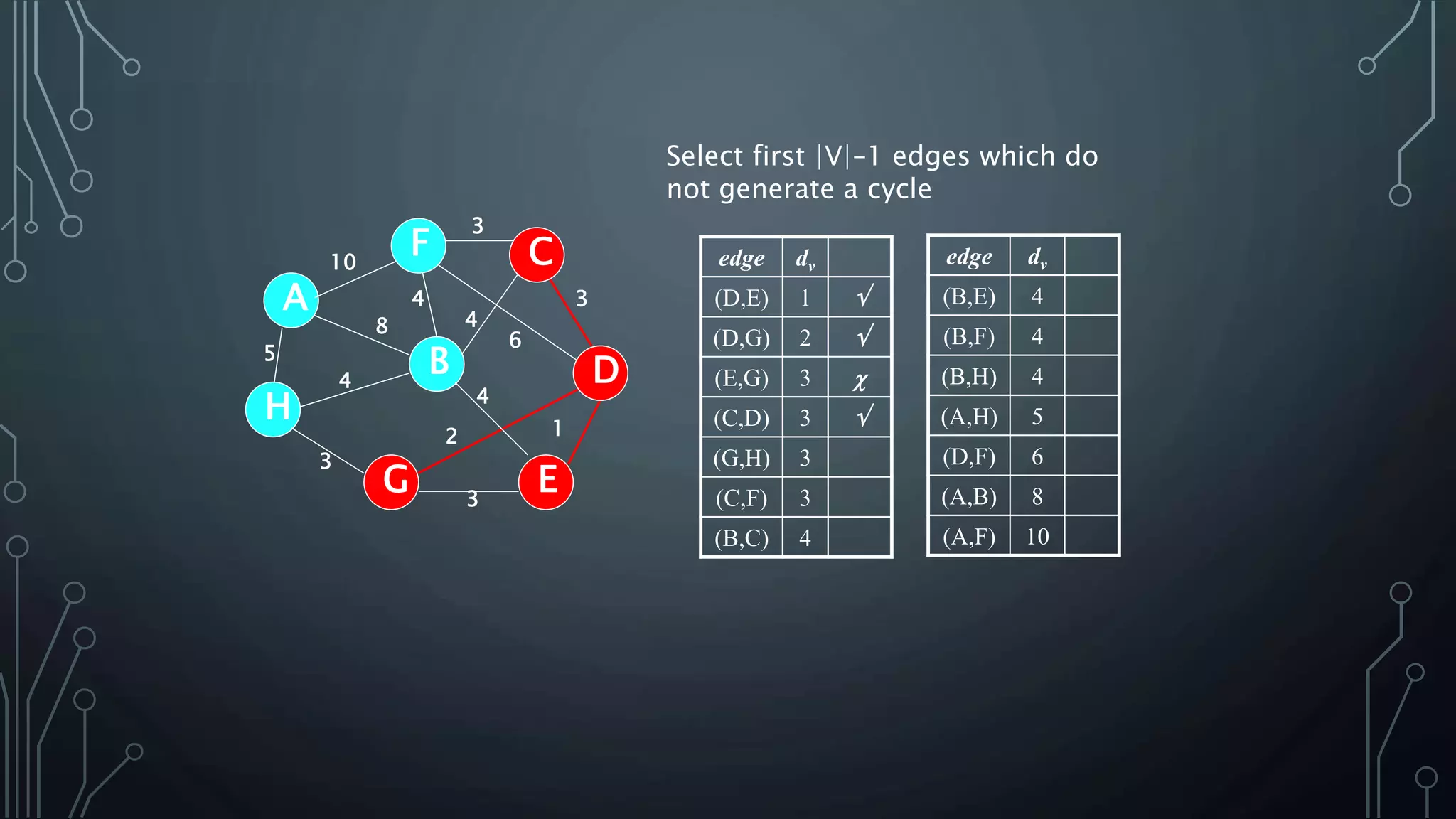
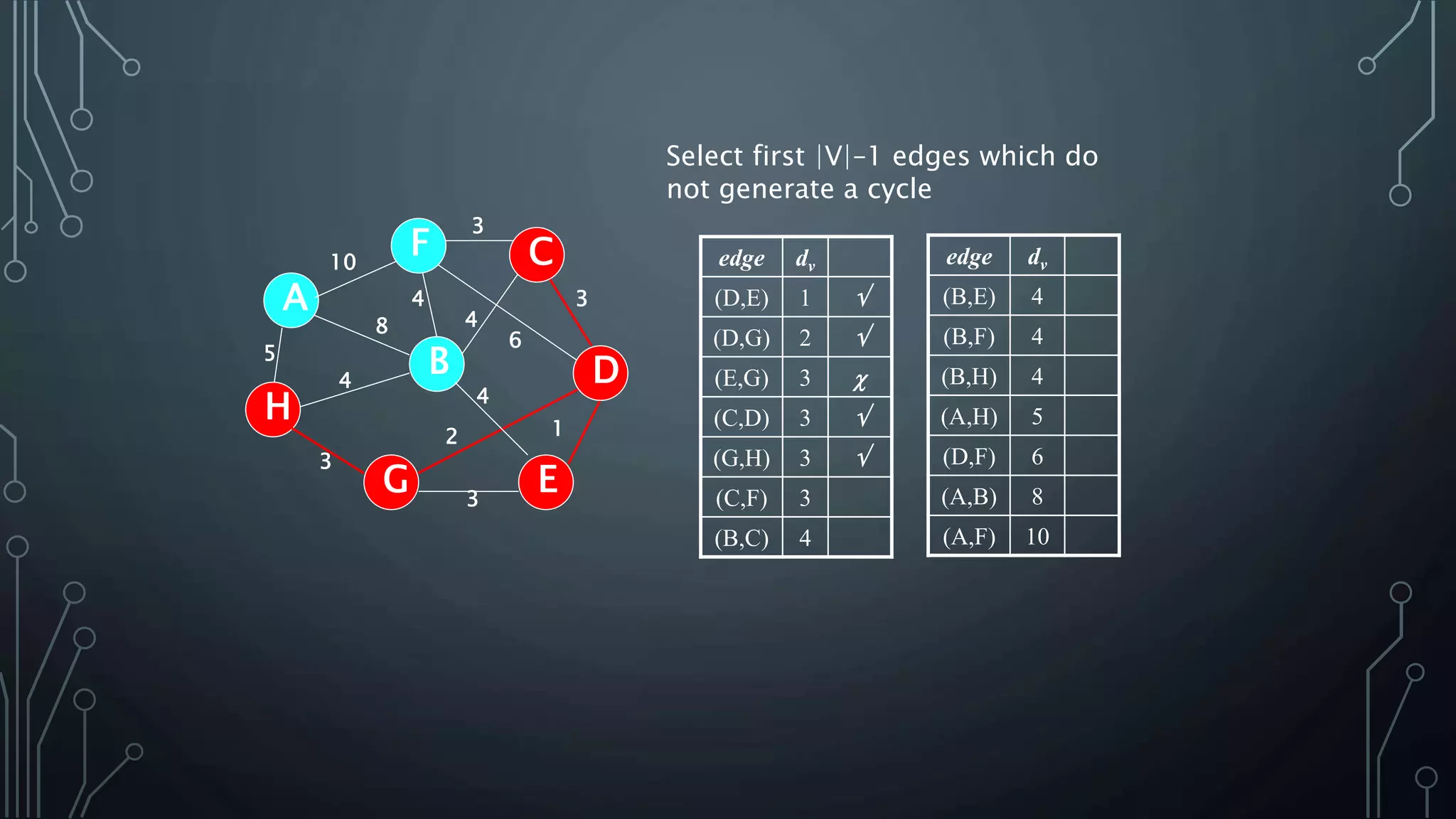
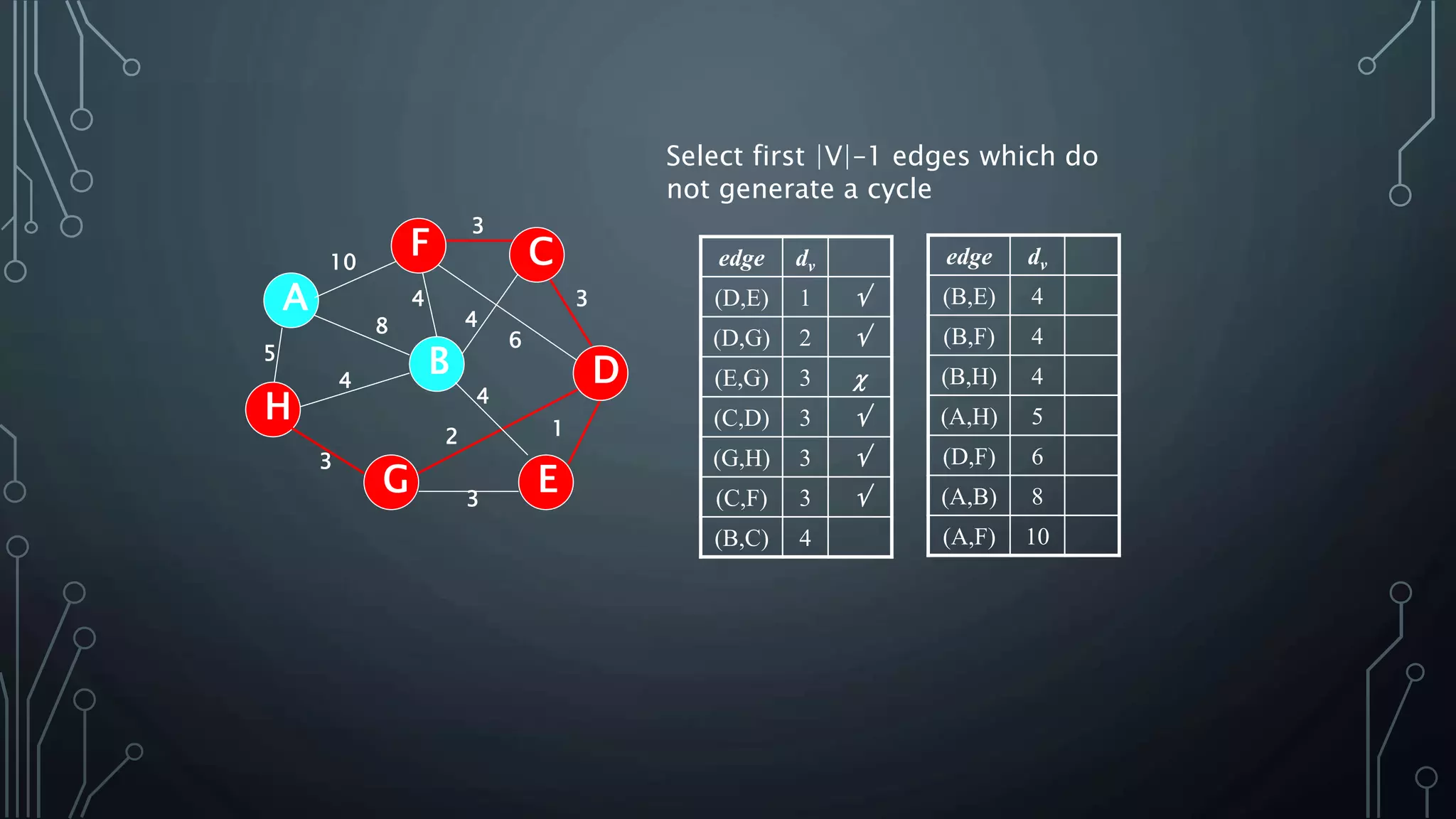
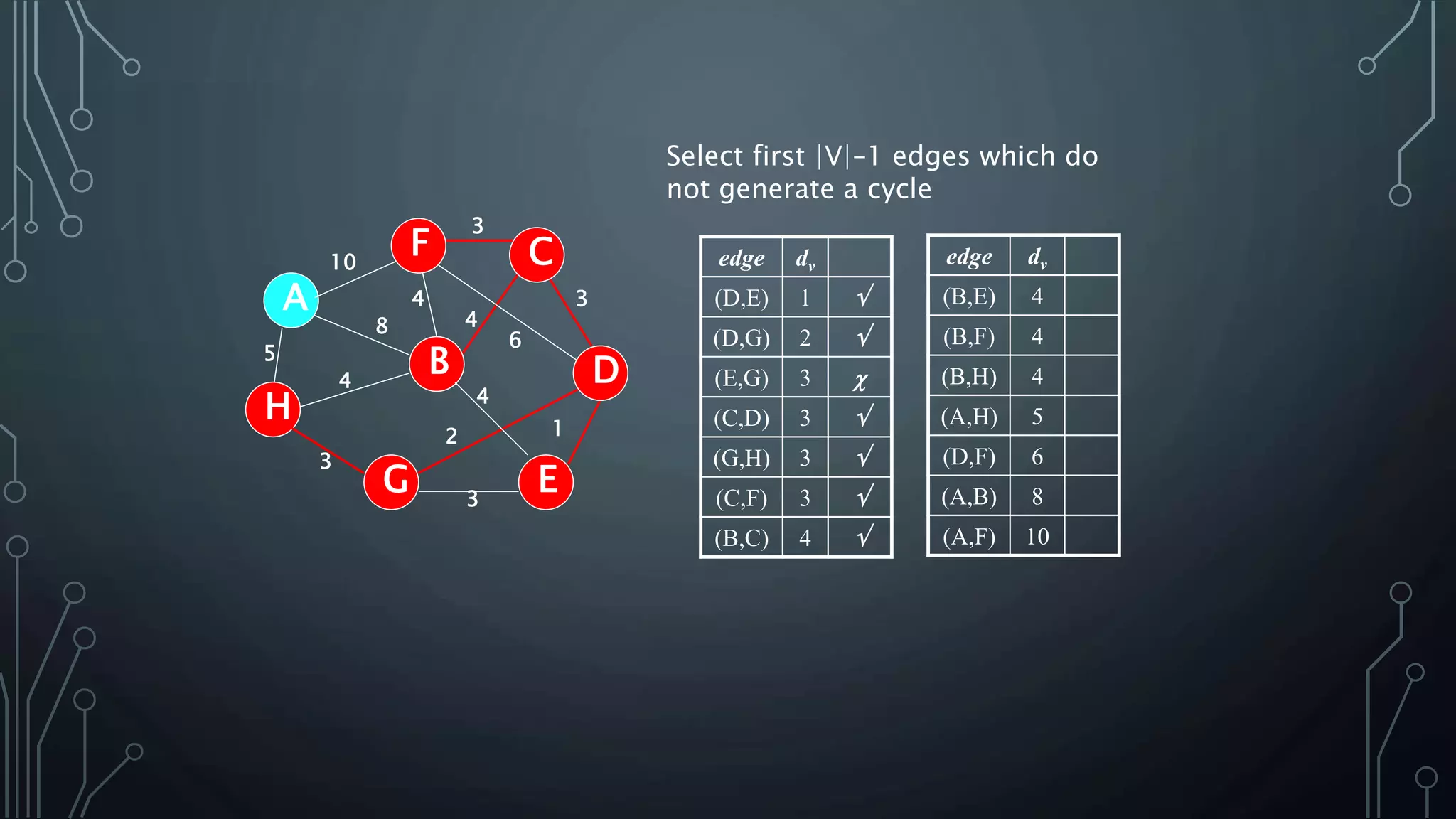
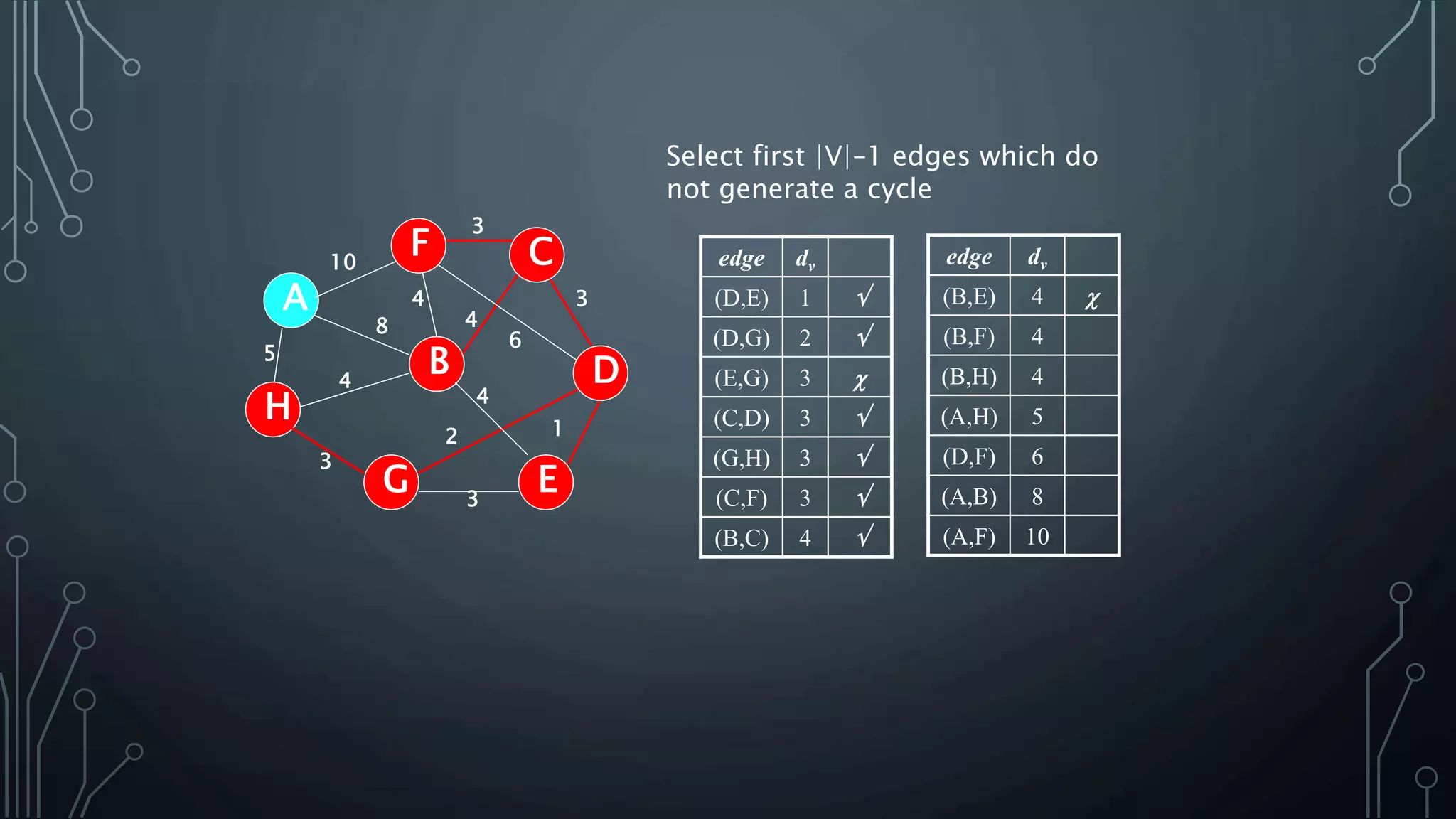
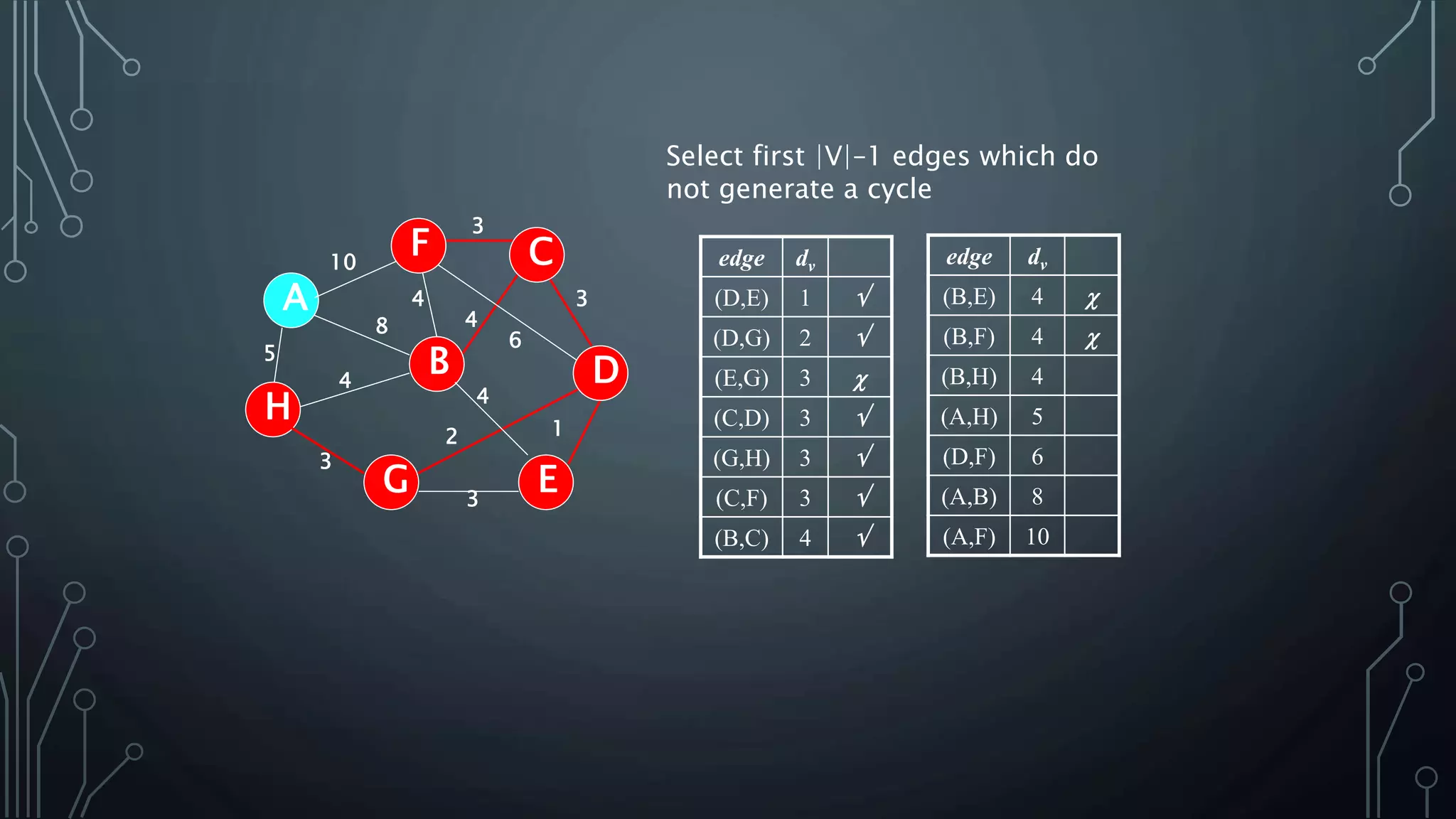
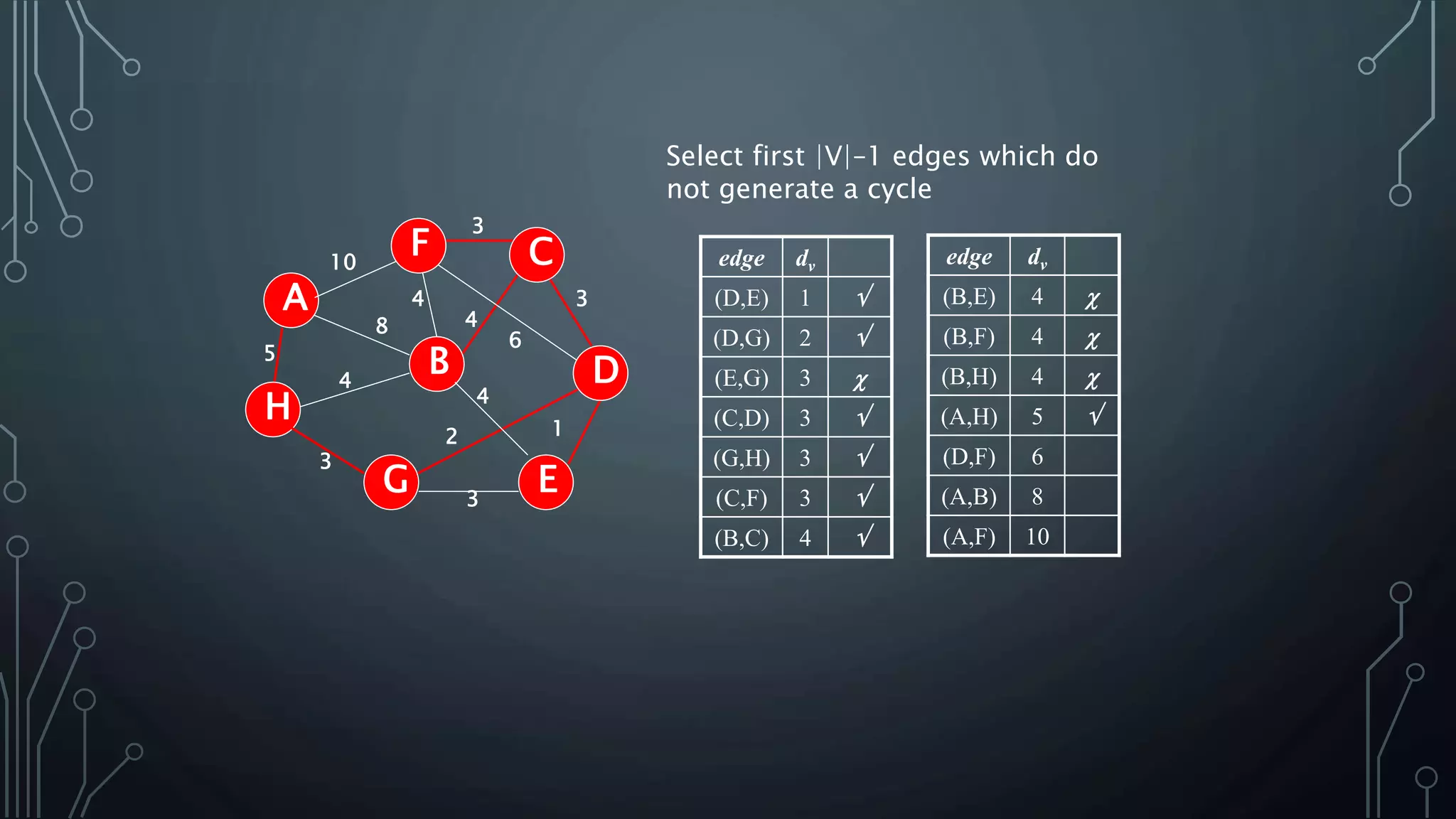
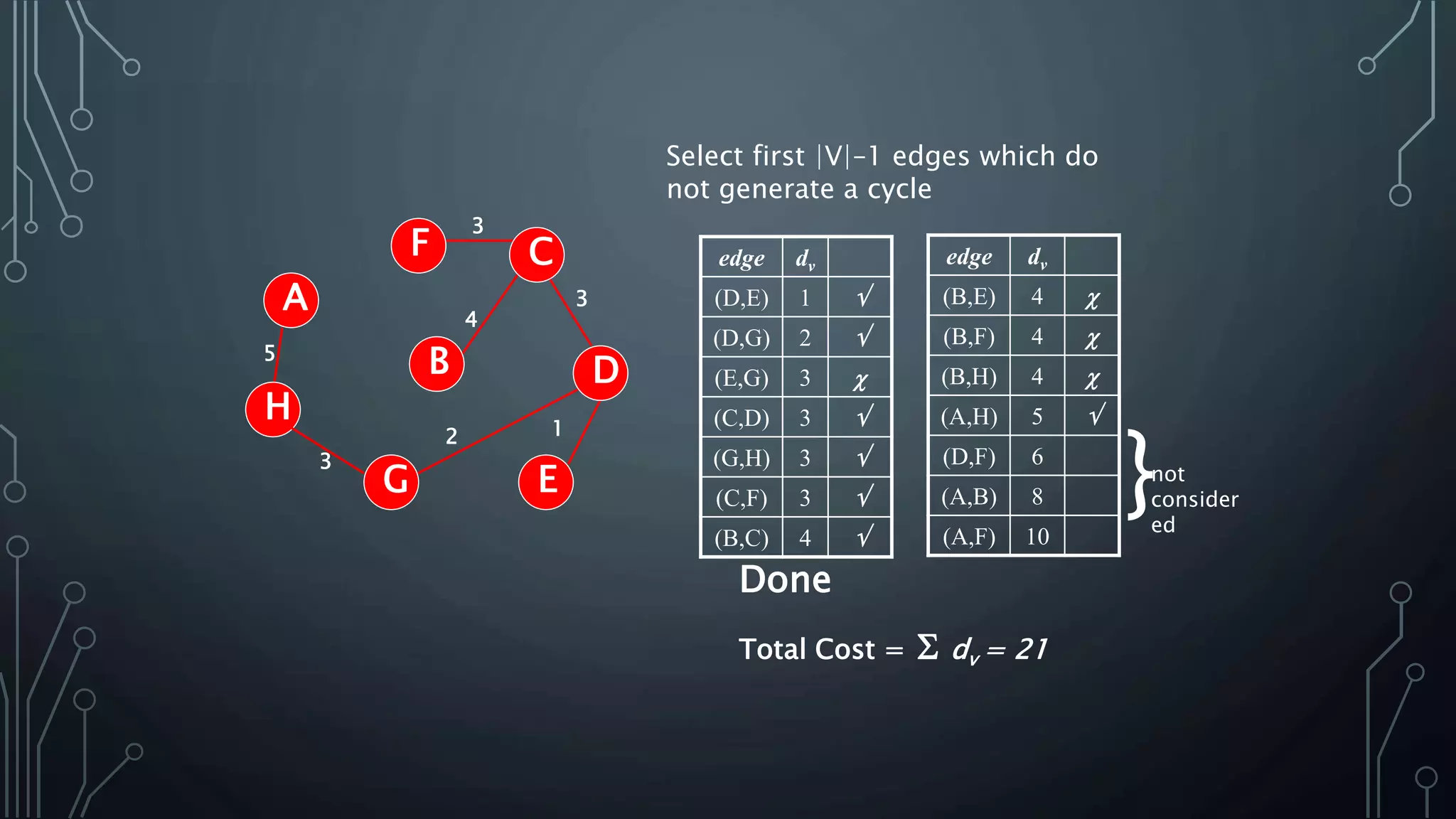
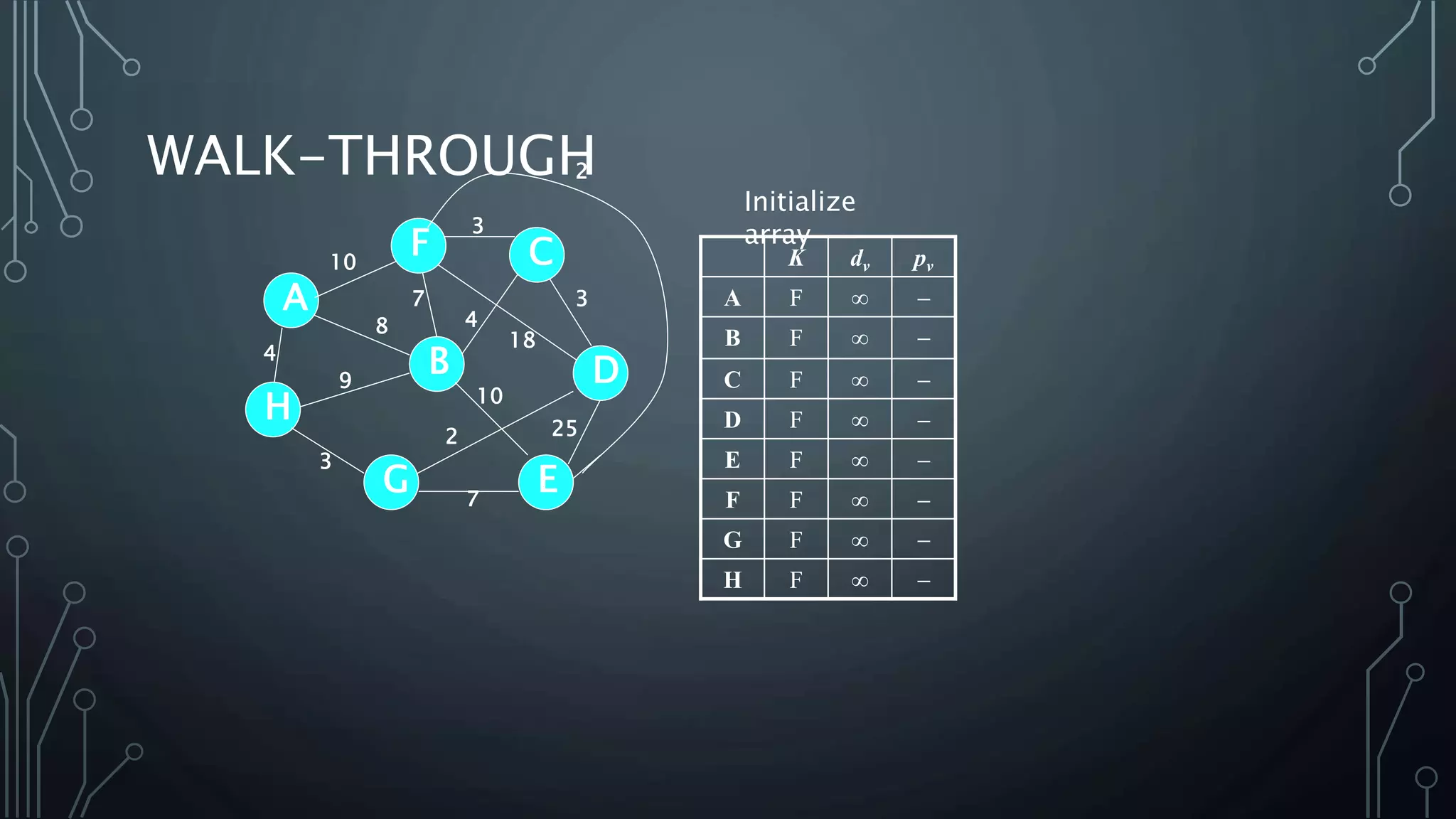
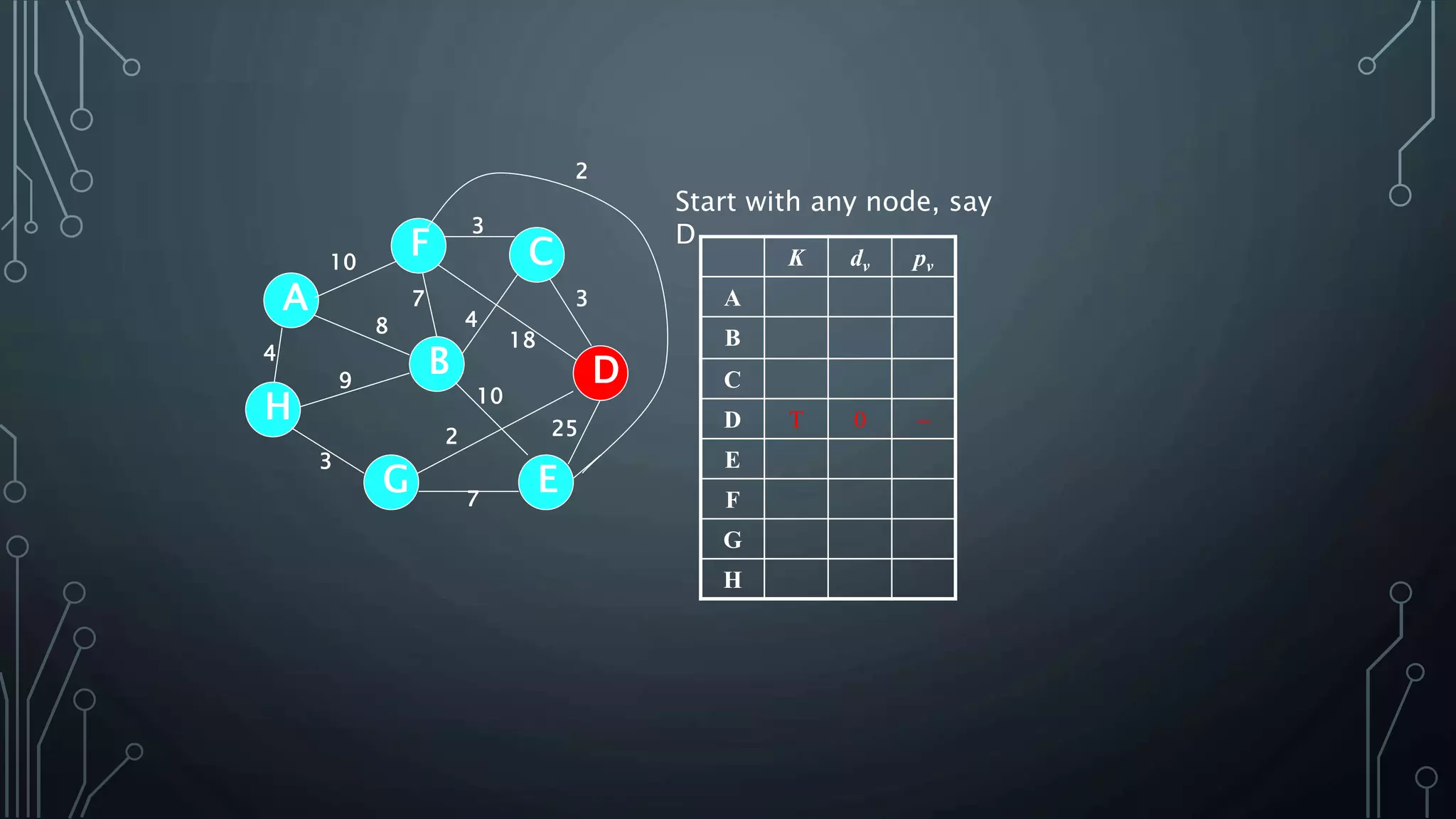
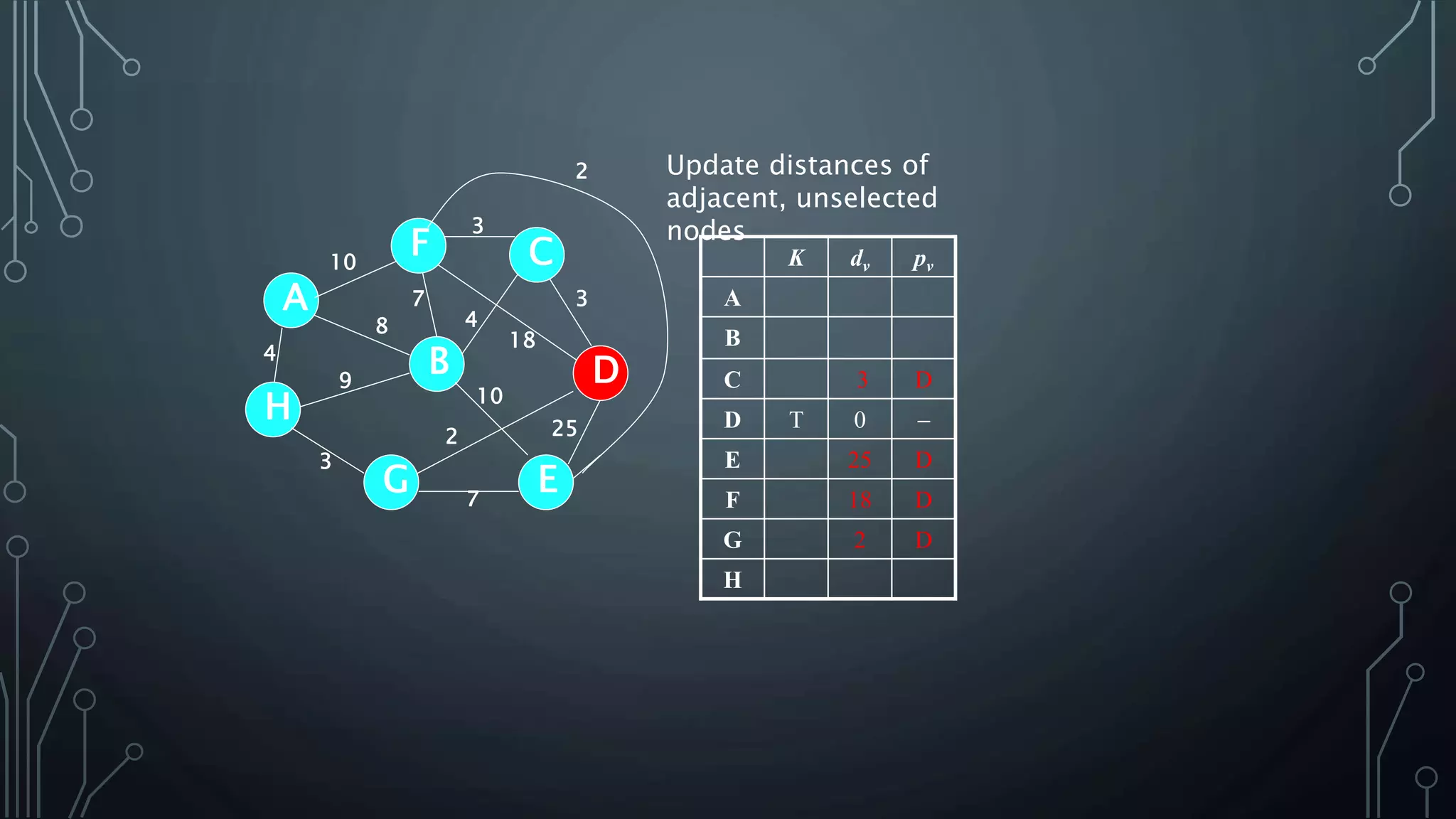
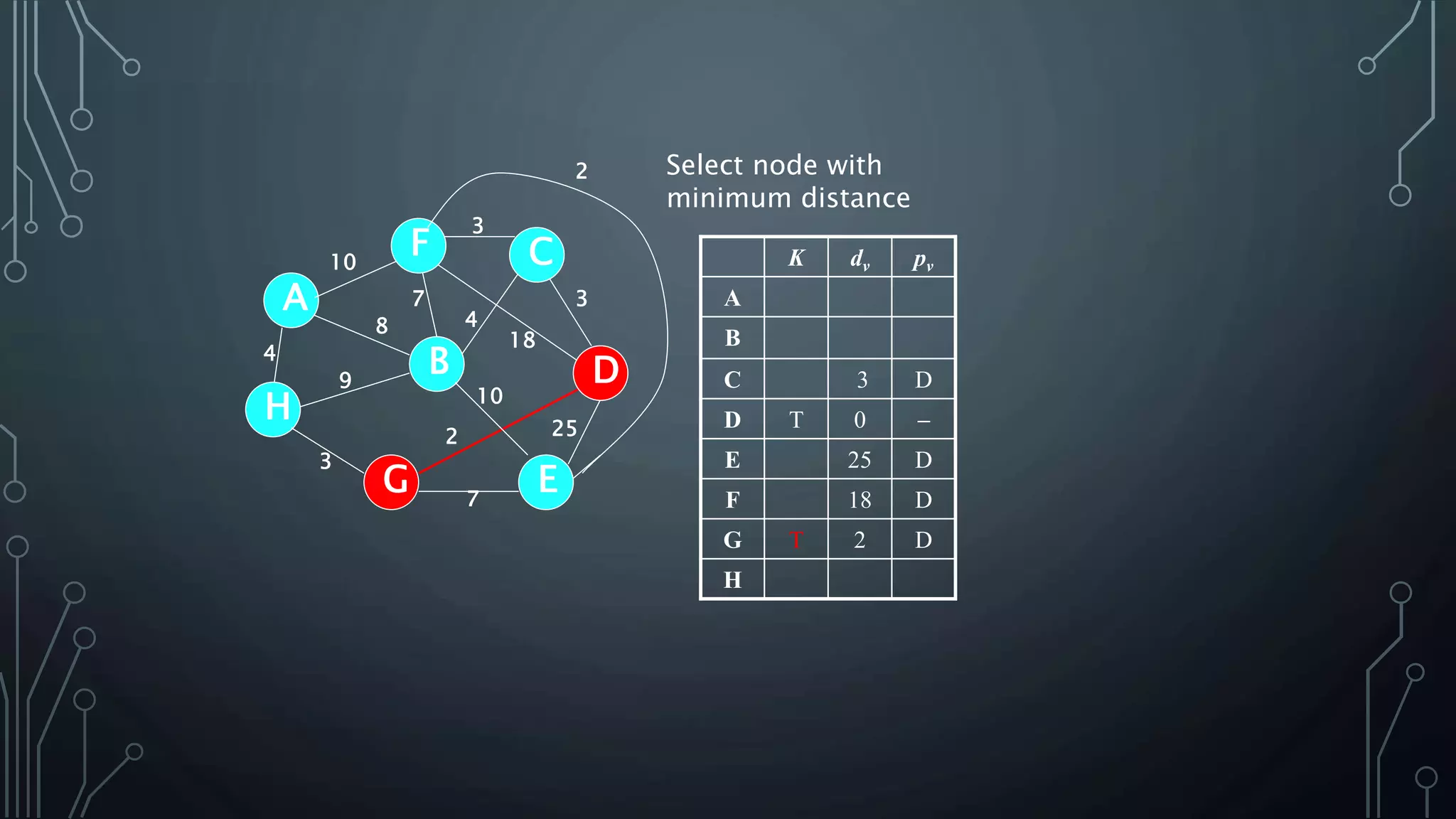
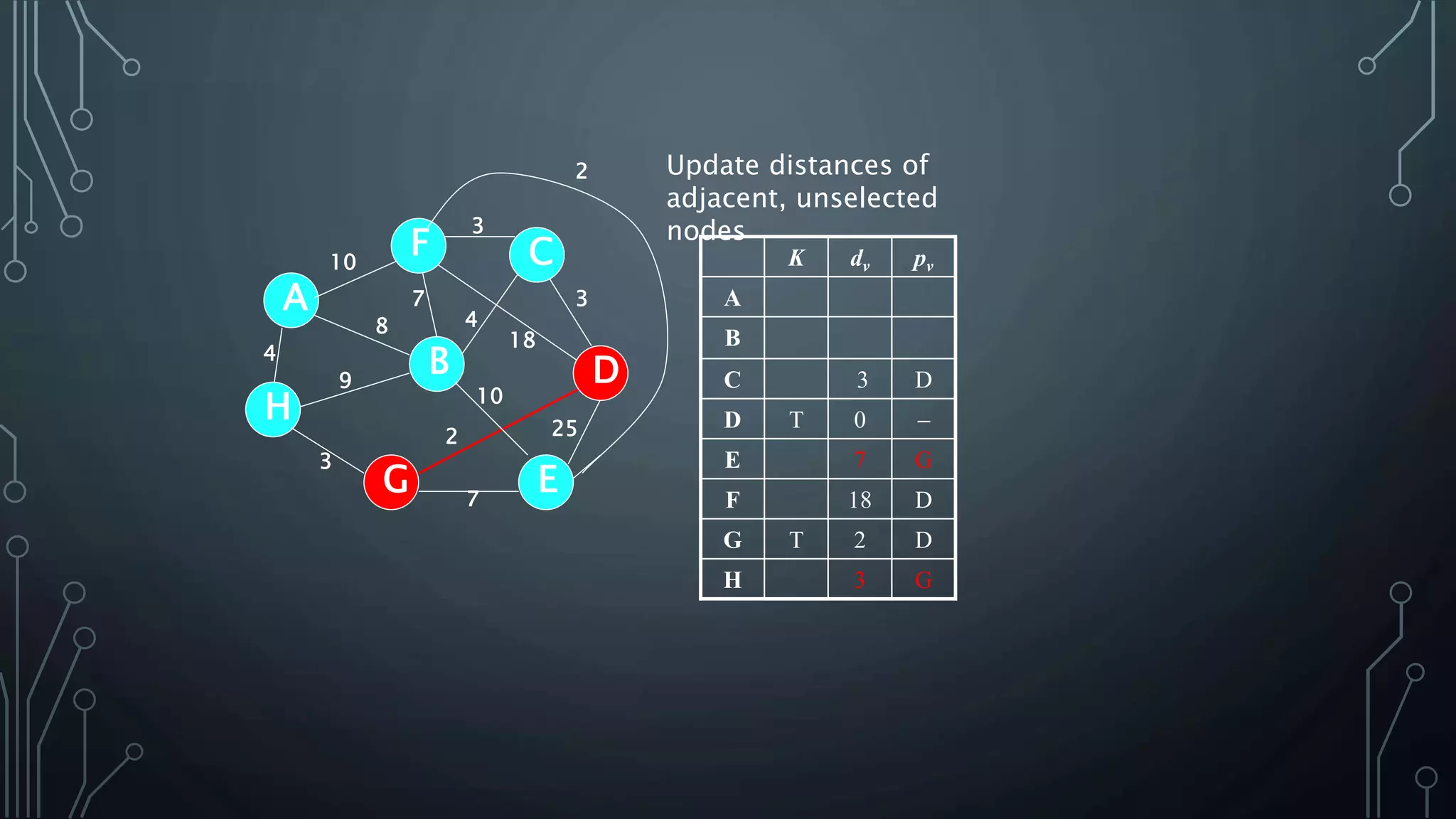
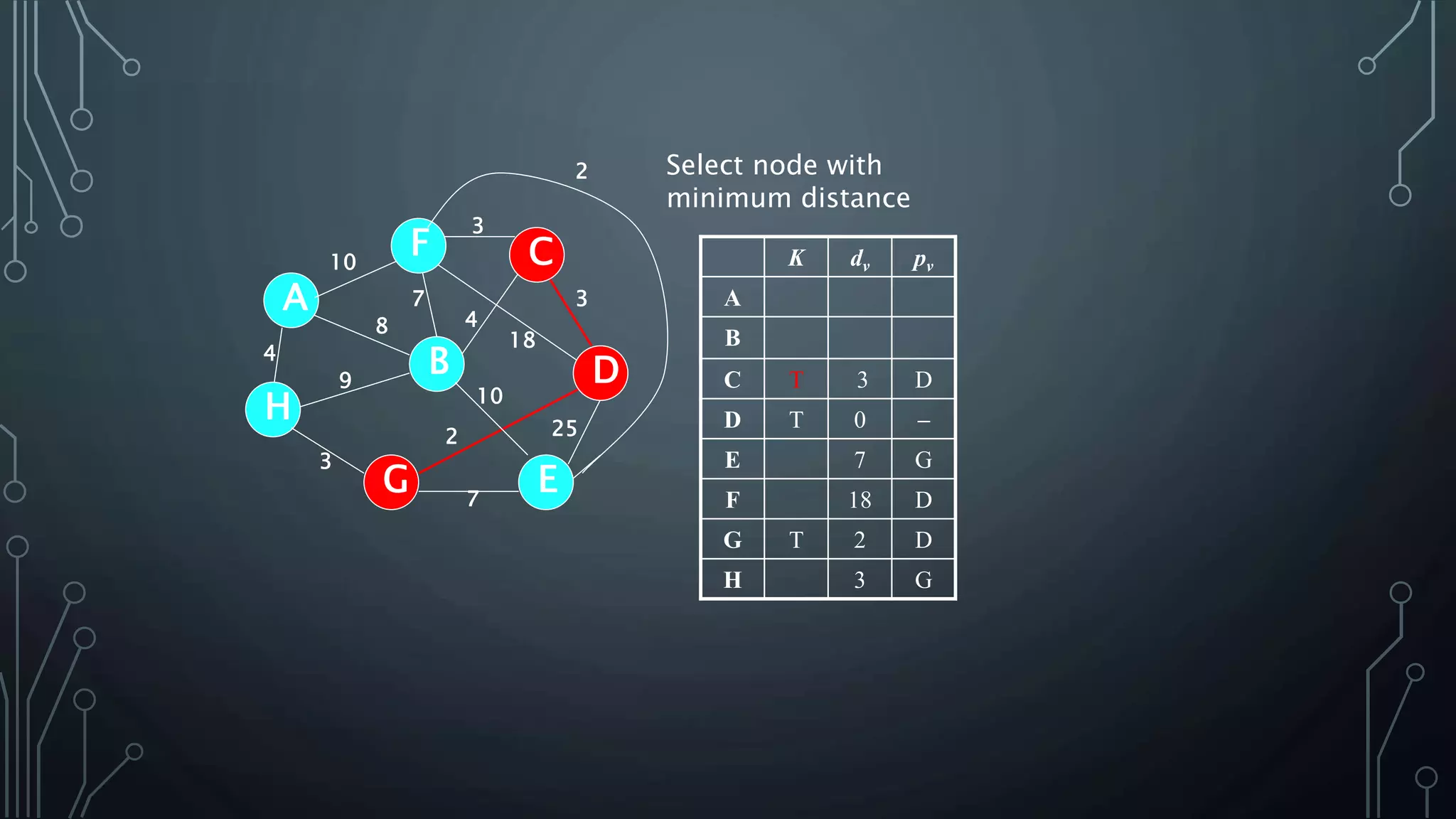
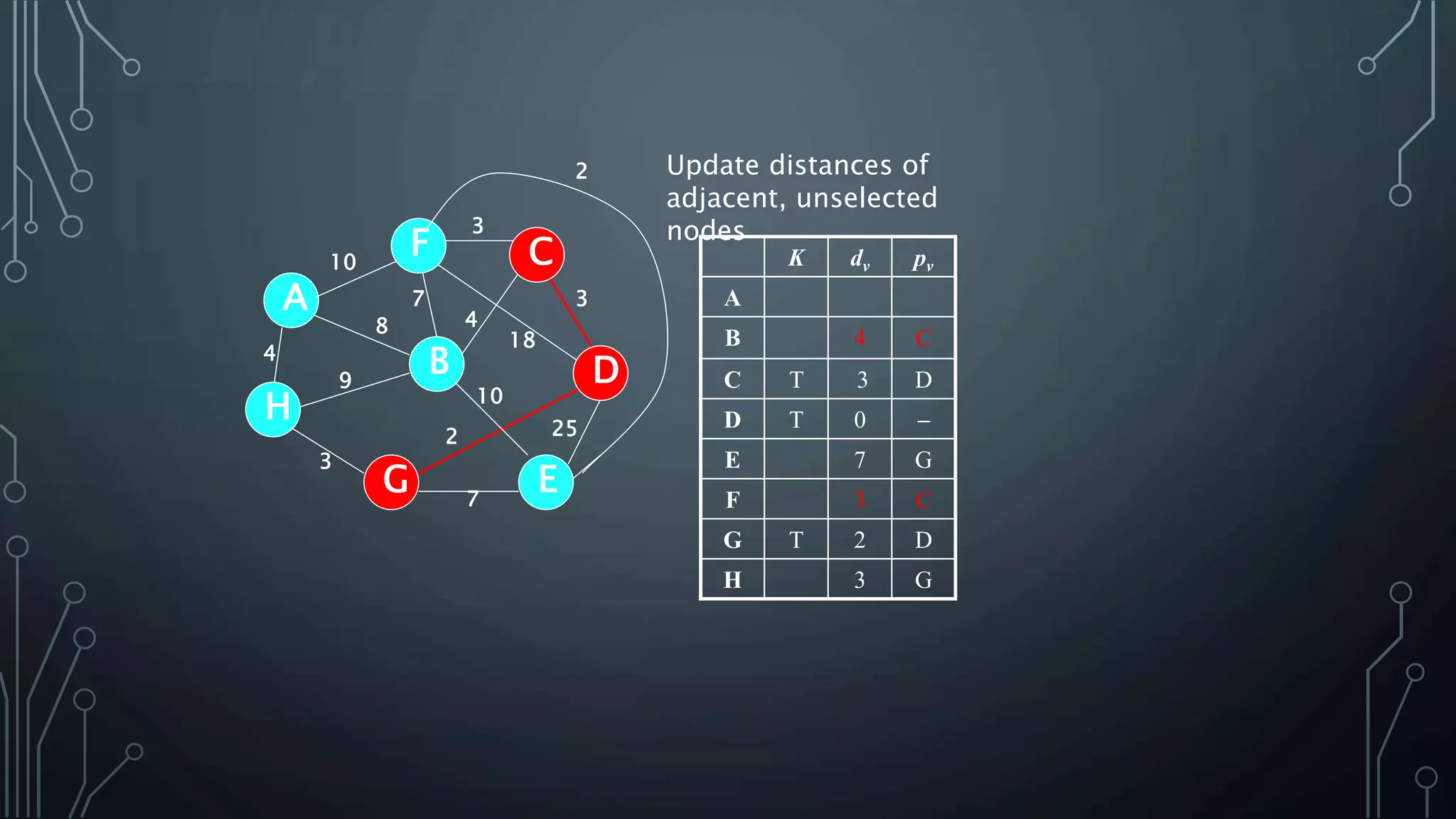
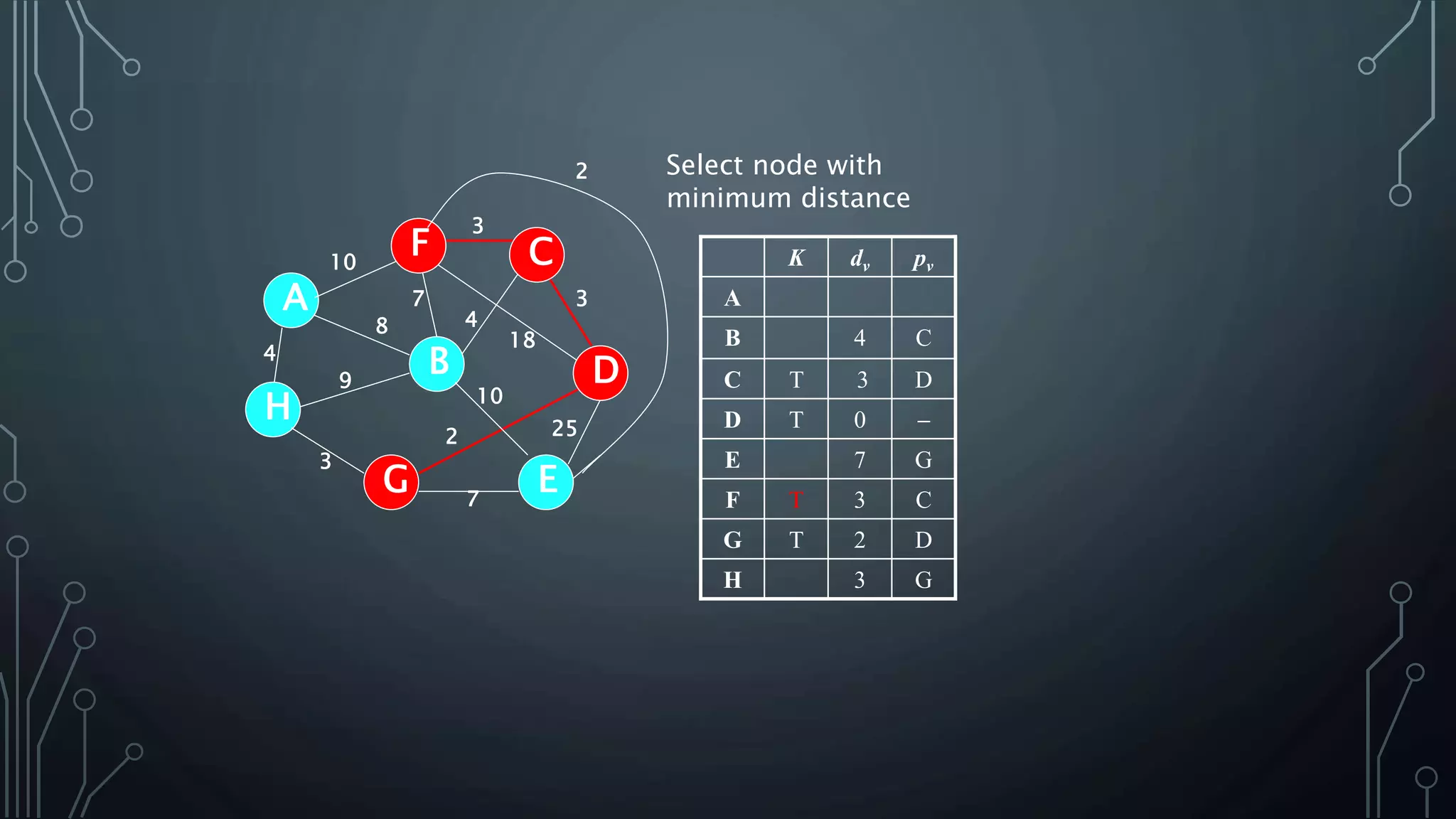
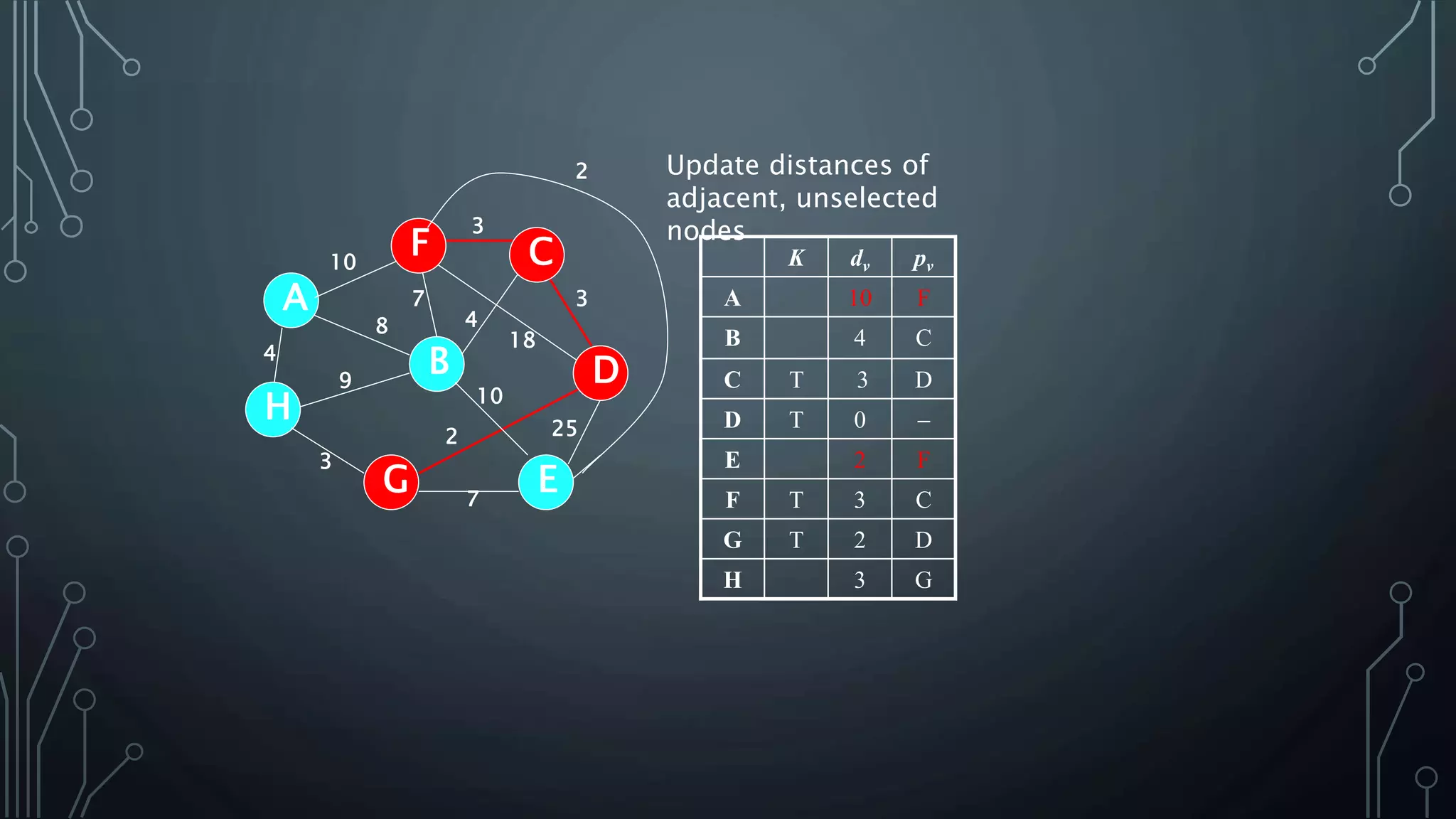
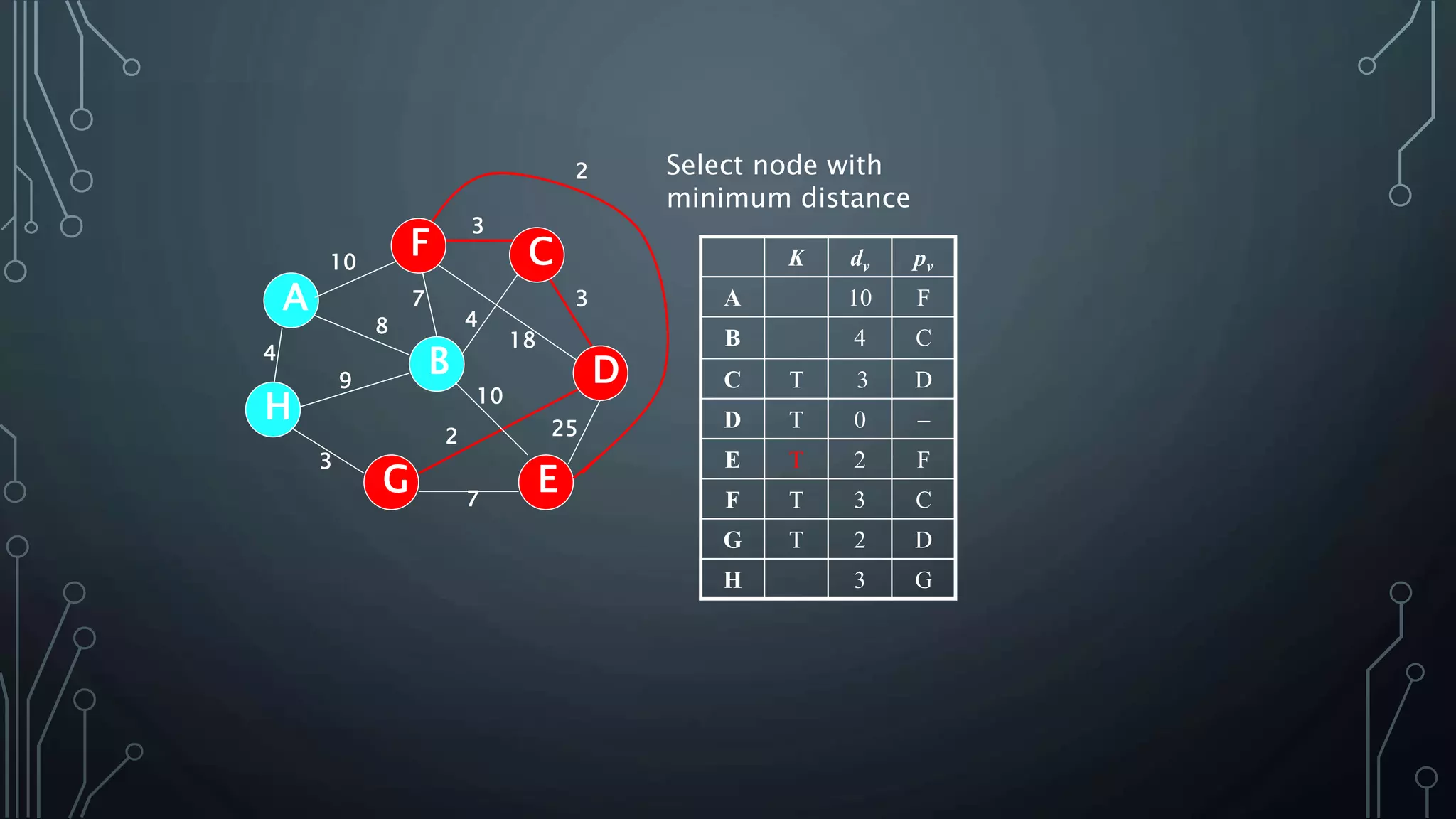
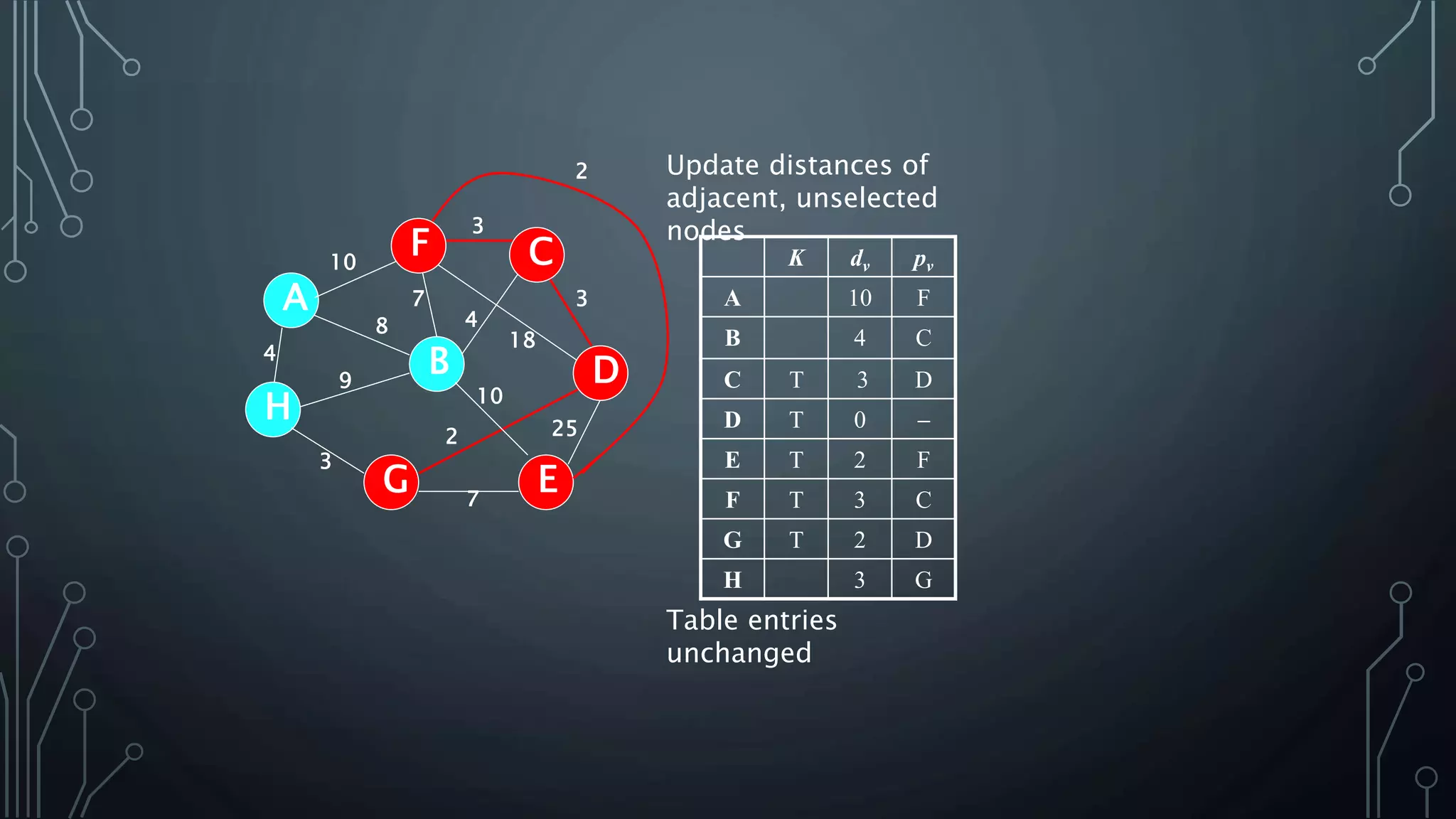
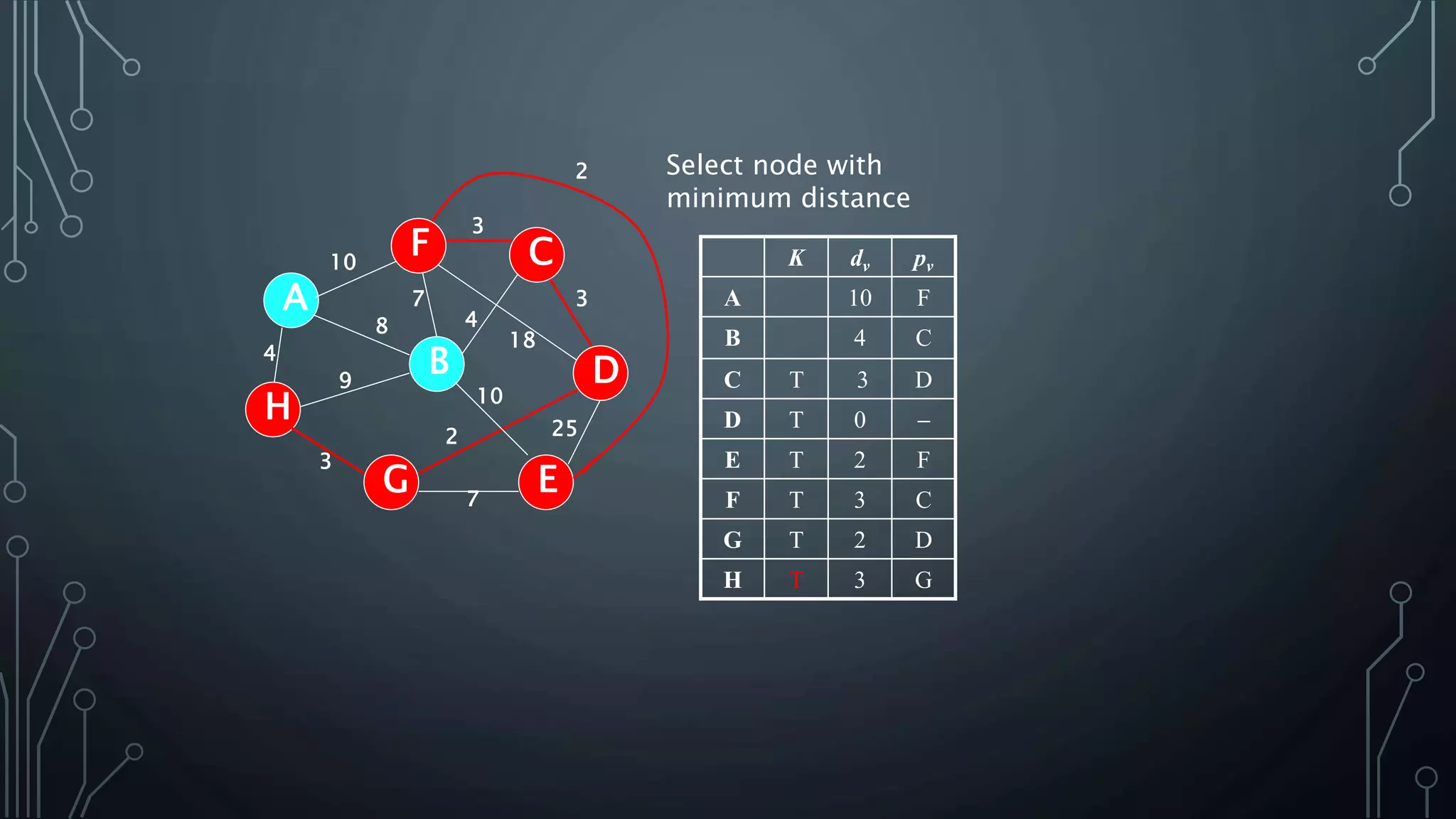
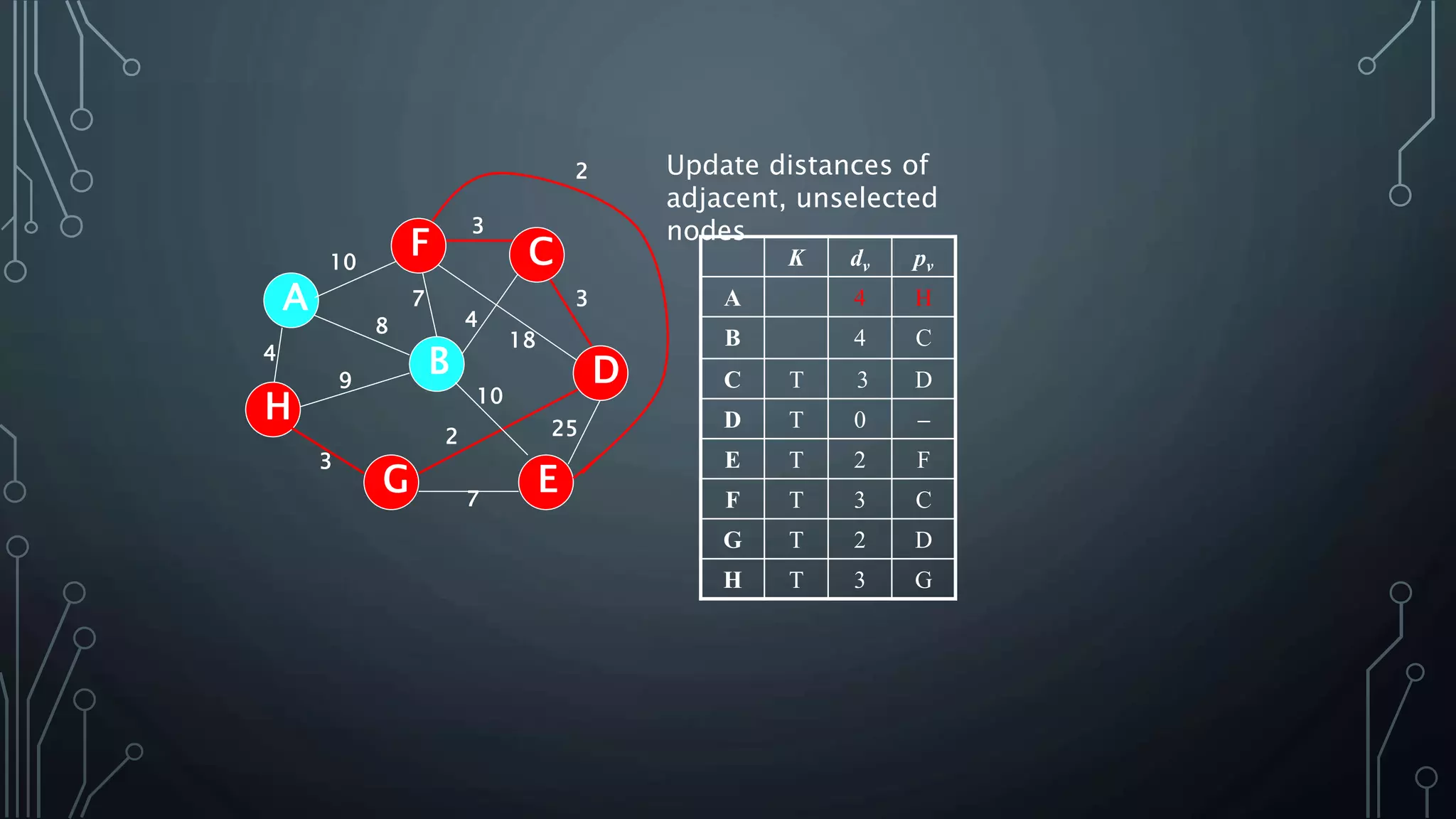
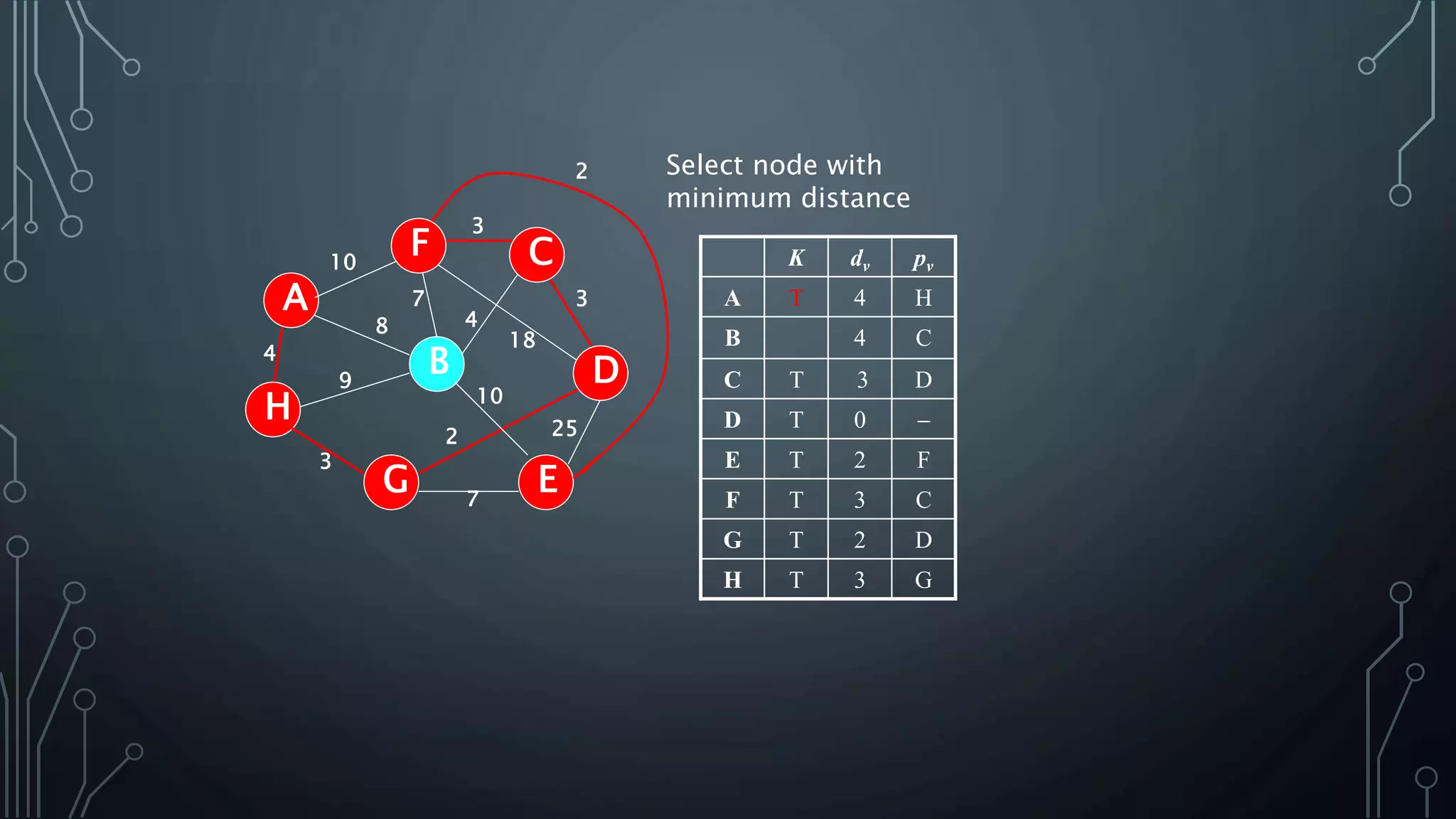
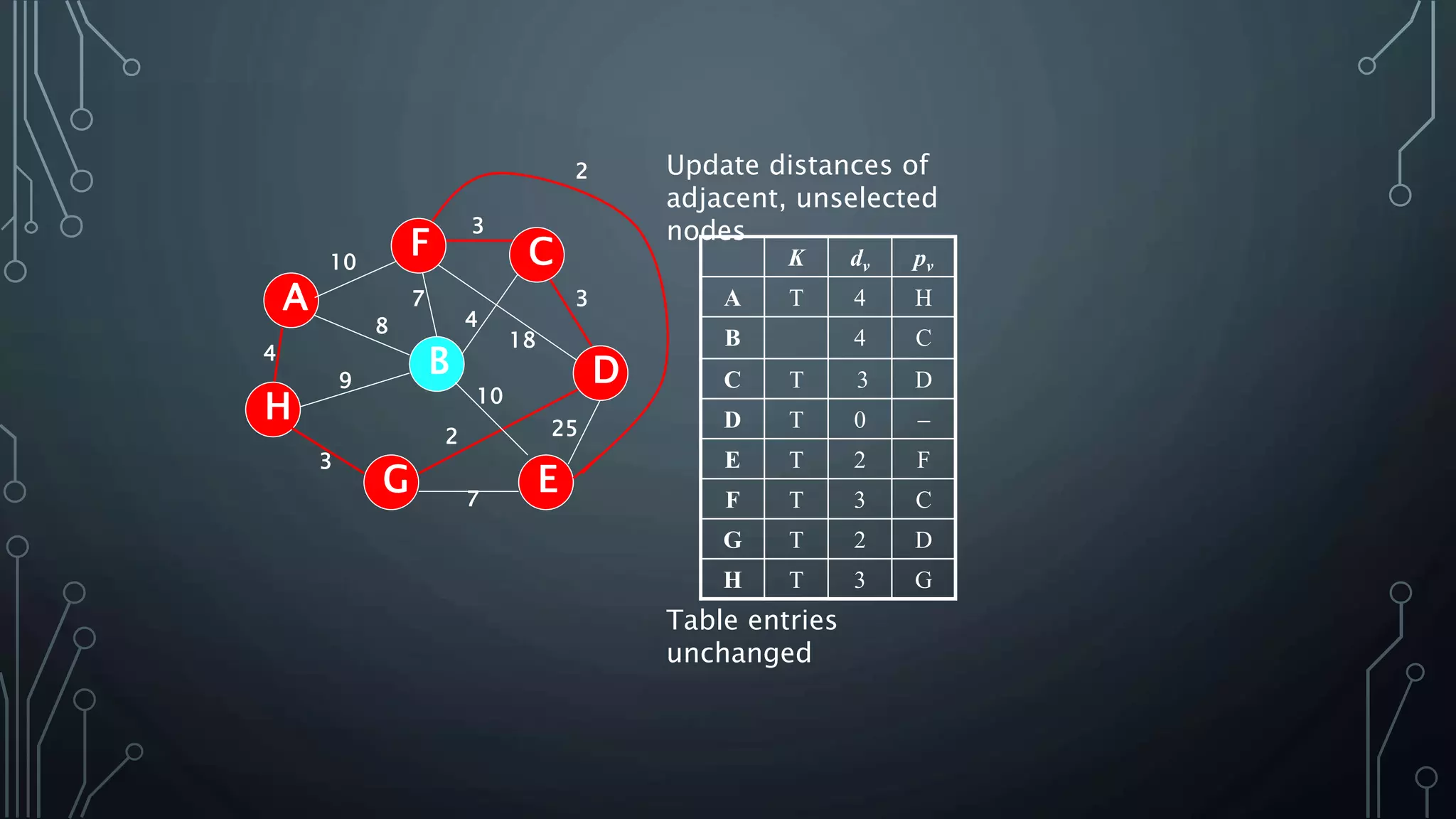
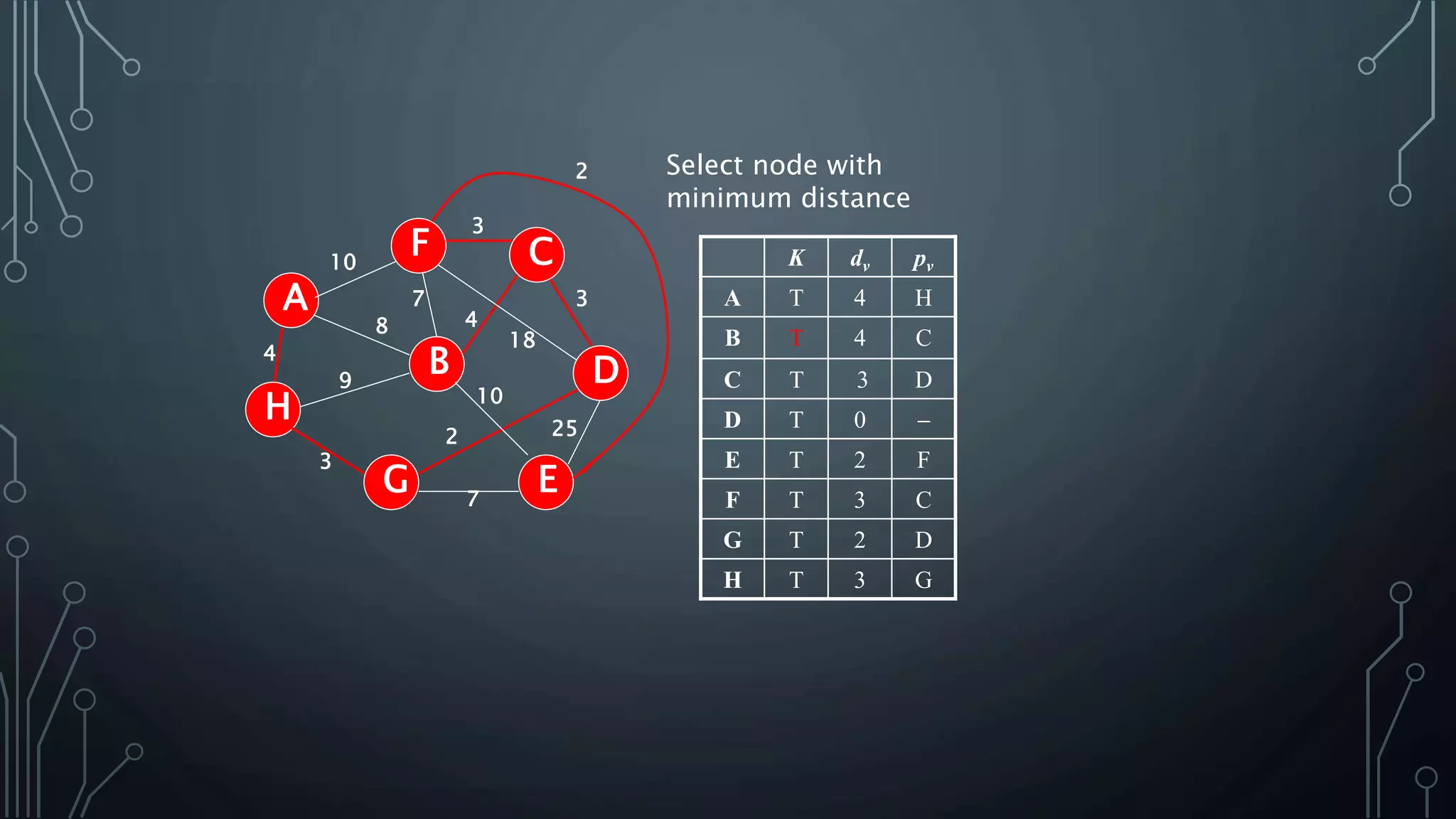
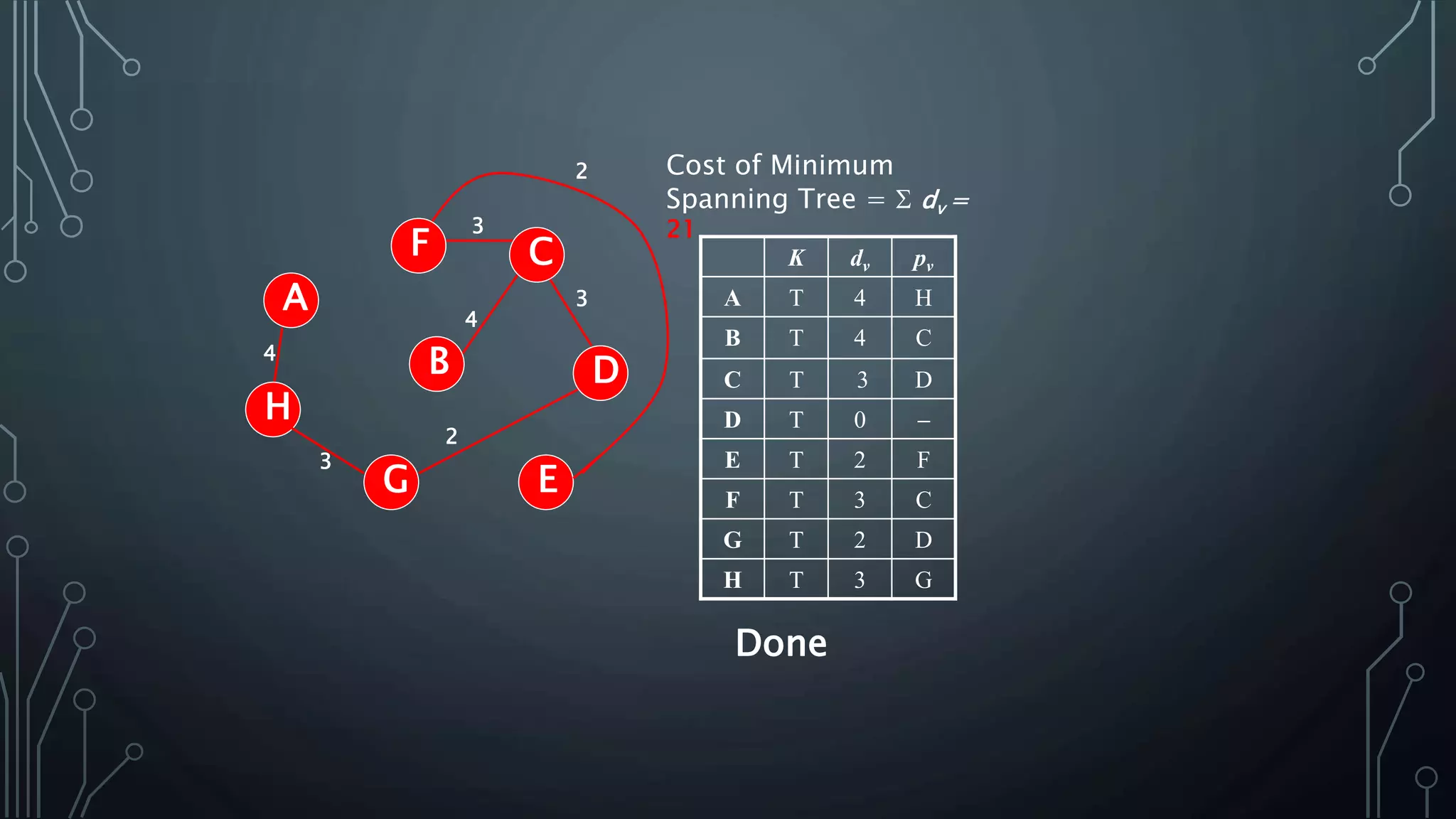
The document discusses Prim's and Kruskal's algorithms for finding a minimum spanning tree (MST) in undirected graphs. It outlines the step-by-step processes for both algorithms, highlighting their greedy nature and optimal solutions. Additionally, it compares the two algorithms, noting that Prim's maintains a tree at all times while Kruskal's can form a forest.

1. A PRESENTATION ON PRIM’S AND
KRUSKAL’S ALGORITHM
By:
Gaurav Vivek Kolekar
and
Lionel Sequeira

2. GRAPHS AND IT’S EXAMPLES

3. MINIMUM COST SPANNING TREE
A Minimum Spanning Tree (MST) is a subgraph of an undirected
graph such that the subgraph spans (includes) all nodes, is
connected, is acyclic, and has minimum total edge weight

4. ALGORITHM CHARACTERISTICS
• Both Prim’s and Kruskal’s Algorithms work with
undirected graphs
• Both work with weighted and unweighted graphs
• Both are greedy algorithms that produce optimal
solutions

5. Kruskal’s algorithm
1. Select the shortest edge in a
network
2. Select the next shortest edge
which does not create a cycle
3. Repeat step 2 until all vertices
have been connected
Prim’s algorithm
1. Select any vertex
2. Select the shortest edge
connected to that vertex
3. Select the shortest edge
connected to any vertex
already connected
4. Repeat step 3 until all
vertices have been
connected

6. Work with edges, instead of nodes of a graph
Two steps:
– Sort edges by increasing edge weight
– Select the first |V| – 1 edges that do not
generate a cycle
KRUSKAL’S ALOGORITHM

7. Consider an undirected, weight
graph
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
WALK-THROUGH

8. Sort the edges by increasing edge
weight
edge dv
(D,E) 1
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

9. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

10. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

11. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Accepting edge (E,G) would create a
cycle

12. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

13. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

14. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

15. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

16. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

17. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

18. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4 
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10

19. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4 
(A,H) 5 
(D,F) 6
(A,B) 8
(A,F) 10

20. Select first |V|–1 edges which do
not generate a cycle
edge dv
(D,E) 1 
(D,G) 2 
(E,G) 3 
(C,D) 3 
(G,H) 3 
(C,F) 3 
(B,C) 4 
5
1
A
H
B
F
E
D
C
G
2
3
3
3
edge dv
(B,E) 4 
(B,F) 4 
(B,H) 4 
(A,H) 5 
(D,F) 6
(A,B) 8
(A,F) 10
Done
Total Cost =  dv = 21
4
}not
consider
ed

21. PRIM’S ALGORITHM

22. WALK-THROUGH
Initialize
array
K dv pv
A F  
B F  
C F  
D F  
E F  
F F  
G F  
H F  
4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
2

23. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Start with any node, say
D
K dv pv
A
B
C
D T 0 
E
F
G
H
2

24. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A
B
C 3 D
D T 0 
E 25 D
F 18 D
G 2 D
H
2

25. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A
B
C 3 D
D T 0 
E 25 D
F 18 D
G T 2 D
H
2

26. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A
B
C 3 D
D T 0 
E 7 G
F 18 D
G T 2 D
H 3 G
2

27. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A
B
C T 3 D
D T 0 
E 7 G
F 18 D
G T 2 D
H 3 G
2

28. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A
B 4 C
C T 3 D
D T 0 
E 7 G
F 3 C
G T 2 D
H 3 G
2

29. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A
B 4 C
C T 3 D
D T 0 
E 7 G
F T 3 C
G T 2 D
H 3 G
2

30. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 
E 2 F
F T 3 C
G T 2 D
H 3 G
2

31. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H 3 G
2

32. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H 3 G
2
Table entries
unchanged

33. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

34. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A 4 H
B 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

35. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A T 4 H
B 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

36. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A T 4 H
B 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Table entries
unchanged

37. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with
minimum distance
K dv pv
A T 4 H
B T 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2

38. 4
A
H
B
F
E
D
C
G
2
3
4
3
3
Cost of Minimum
Spanning Tree =  dv =
21
K dv pv
A T 4 H
B T 4 C
C T 3 D
D T 0 
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Done

39. DIFFERENCE BETWEEN PRIM’S AND
KRUSKAL’S ALGORITHM
• The difference between Prim’s algorithm and Kruskal’s
algorithm is that the set of selected edges forms a tree at all
times when using Prim’s algorithm while a forest is formed
when using Kruskal’s algorithm.
• In Prim’s algorithm, a least-cost edge (u, v) is added to T such
that T∪ {(u, v)} is also a tree. This repeats until T contains n-1
edges.

40. •Both algorithms will always give solutions with
the same length.
•They will usually select edges in a different order.
•Occasionally they will use different edges – this
may happen when you have to choose between
edges with the same length.
SOME POINTS TO NOTE

41. READINGS