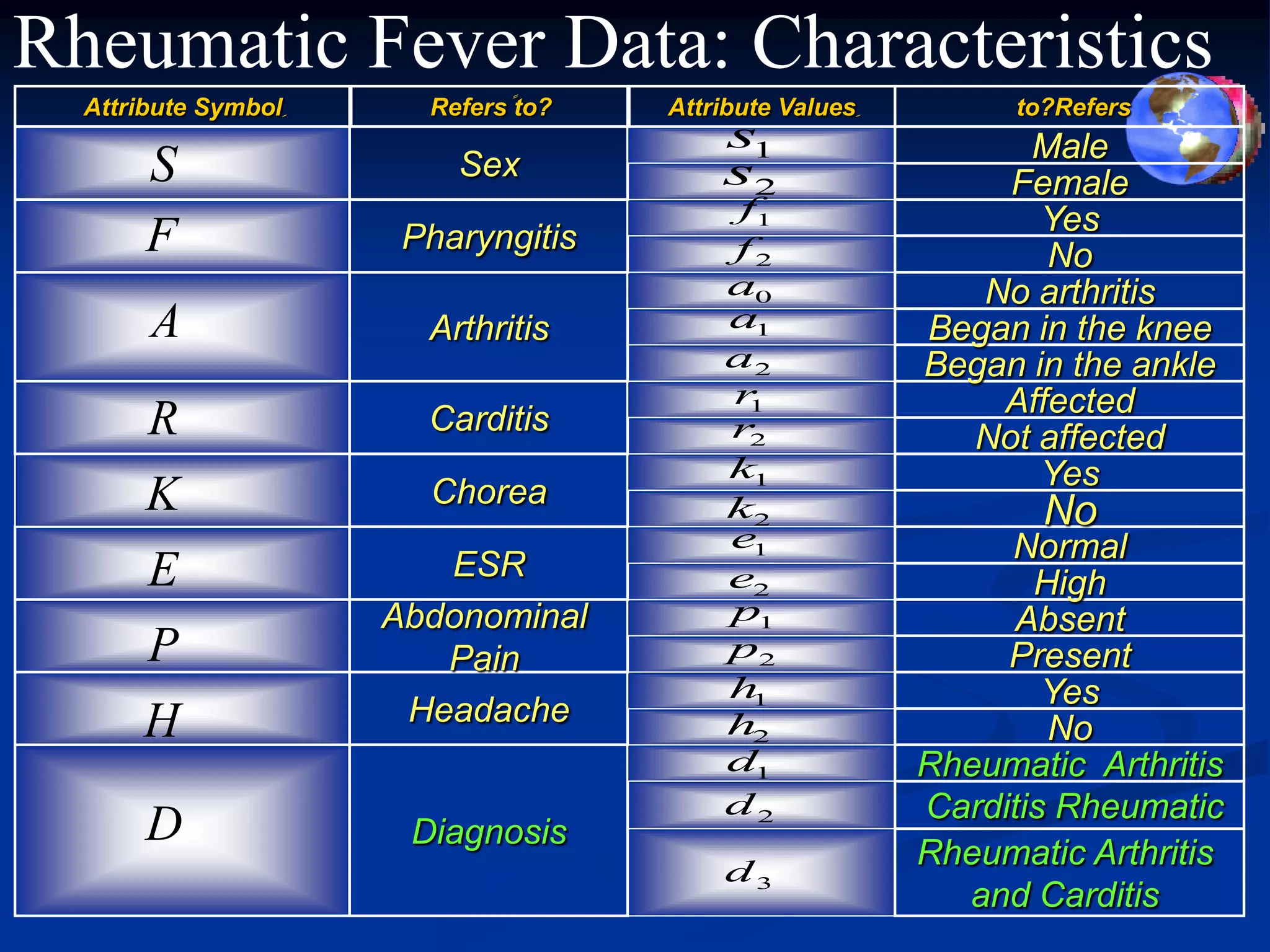
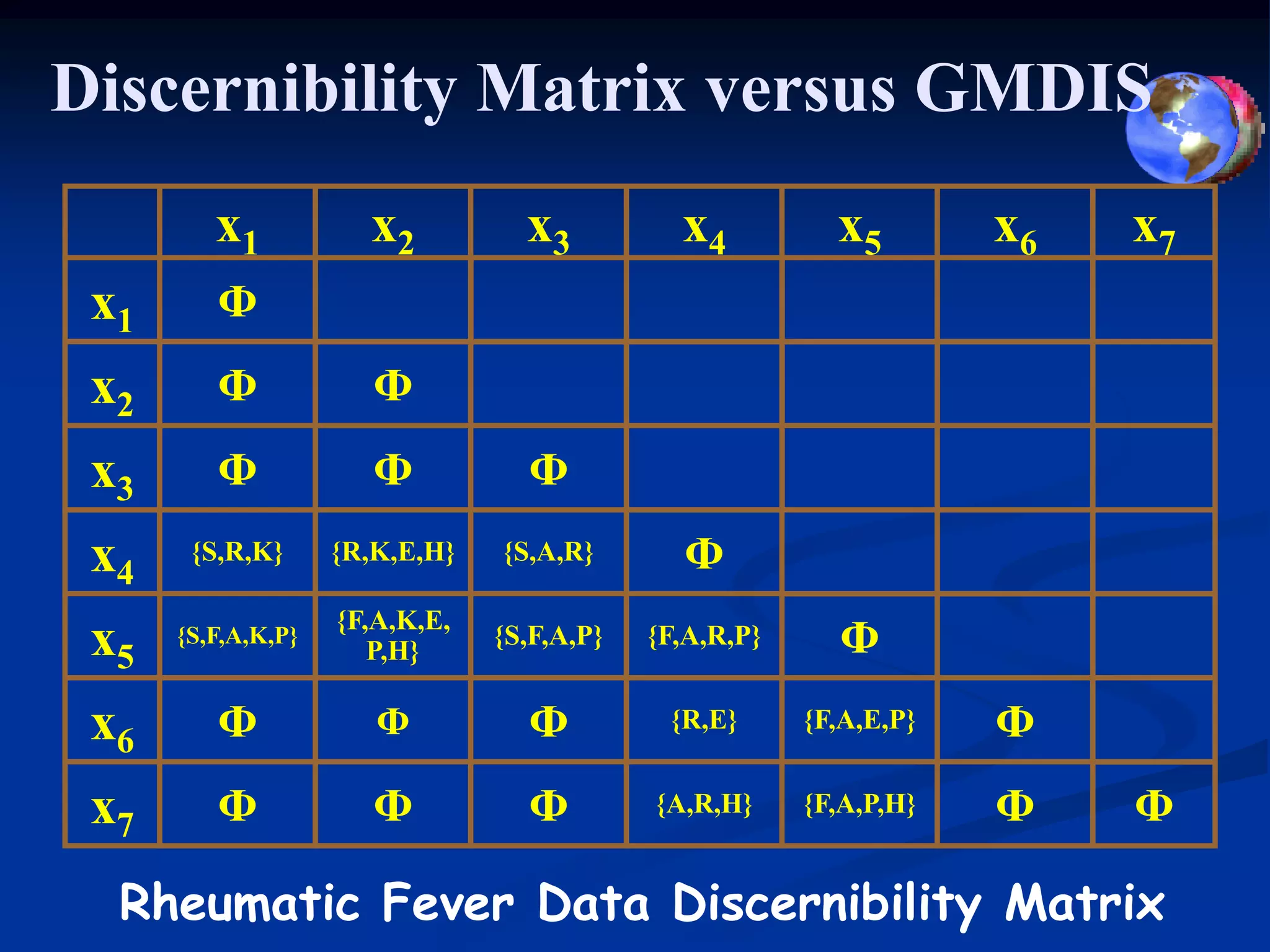
This document proposes new approaches for data reduction in generalized multi-valued decision information systems (GMDIS). It introduces the concept of GMDIS, which generalizes rough set theory to allow attributes to take set values. Two relations are defined on condition and decision attributes to form new equivalence classes for reduction. The degree of dependency between attributes is also studied. As a case study, rheumatic fever patient data is converted to a GMDIS and new reduct algorithms are applied. The results show the new approach provides a more refined reduction of the data compared to traditional rough set methods.

1. New Approaches for Data
Reduction in Generalized
Multi-valued Decision
Information System (GMDIS):
Case Study of
Rheumatic Fever Patients
2006

2. By
Abd El-Monem M. Kozea,
Mohamed M. E. Abd El-Monsef,
Mathematics Department, Faculty of Science,
Tanta University, Egypt
Email: akozae55@yahoo.com
Email: mme1976@yahoo.com
&
Soaad Abd El-Badie Attia El-Afify
Computer Science Department,
Cairo Computer Academy (CCA)
Email: savvymore@yahoo.com
Homepage: www.savvymore.mysite.com

3. Outline
 Motivation / Introduction
 Basic Concepts of Rough Sets
 Rheumatic Fever Data: Characteristics
 New Thinking
 Generalized Multi-Valued Decision Information System
(GMDIS)
 New Approaches for Data Reduction in GMDIS
 Non-equivalence Relations,
 Topological Spaces and
 Degree of Dependencies in GMDIS
 Reduct Algorithms based on GMDIS
 Rheumatic Fever GMDIS Reduction: Worked example
 Conclusion and Future Work
 Acknowledgment

4. Motivation / Introduction
 Rough set theory was developed by Zdzislaw Pawlak in
the early 1982’s.
 RS is based on the idea of equivalence relations
which partition the domain into different classes.
 It is a mathematical tool for dealing with incomplete
data for induction of approximations of concepts and
for discovering patterns hidden in data.
 It can be used for feature selection, data reduction,
identifies partial/total dependencies in data, gives
approach to null values and missing data, and
decision rule generation.

5. Motivation / Introduction
 Rough Set Features:
 It is applicable to problems with both
numeric and descriptive attributes
 It is capable of finding all minimal knowledge
representation
 It is highly automated based on strict rules.
 A multi-valued information system (MIS) is a
generalization of the idea of a single valued
information system (SIS).
 In a multi-valued information system,
 Attribute functions are allowed to map
elements to sets of attribute values.

6. Rough Set Theory:
Basic Concepts
 Information/Decision Systems (Tables)
 Indiscernibility
 Set Approximation
 Reducts and Core
 Rough Membership
 Dependency of Attributes

7. Information Systems Types
The first concept of IS was developed by
Grzymala-Busse (1988). There are many types of
IS as follows:
 Single valued Information System (SIS)
 The data takes a single value for each element
 Single valued Decision Information System (SDIS)
 A Multi-valued Information System (MIS)
An ordinary information system which its values ore sets
= (U , At ,{Va : a  At }, f a )
 A Multi-valued Decision Information System (MDIS)
= (U , At U D, {Va : a  At}, f a )

8. Rheumatic Fever Data:
Characteristics
 We obtained the used Rheumatic Fever patients data
from Tanta University Hospital, Egypt.
 All patients are between 9-12 years old with history
of Arthritis began from age 3-5 years.
 This disease has many symptoms and it is usually
started in young age and still with the patient along
his life.
 The following table shows seven patients
characterized by 8 symptoms (attributes) using them
to decide the diagnosis for each patient (decision
attribute).

9. Rheumatic Fever Data: Characteristics
Attribute Symbolِ Refersً to? Attribute Valuesِ to?Refers
s1 Male
S Sex s2 Female
f1 Yes
F Pharyngitis f2 No
a0 No arthritis
A Arthritis a1 Began in the knee
a2 Began in the ankle
r 1 Affected
R Carditis r2 Not affected
k1 Yes
K Chorea k2 No
e1 Normal
E ESR e2 High
Abdonominal p1 Absent
P Pain p2 Present
h 1 Yes
H Headache h2 No
d1 Rheumatic Arthritis
d2 Carditis Rheumatic
D Diagnosis
Rheumatic Arthritis
d3
and Carditis

10. Worked Example 1 (SDIS ):
Rheumatic Fever SDIS Data
S F A R K E P H D
x1 s2 f1 a1 r1 k1 e1 p1 h2 d3
x2 s1 f1 a1 r1 k1 e2 p1 h1 d3
x3 s2 f1 a2 r1 k2 e1 p1 h2 d3
x4 s1 f1 a1 r2 k2 e1 p1 h2 d1
x5 s1 f2 a0 r1 k2 e1 p2 h2 d2
x6 s1 f1 a1 r1 k2 e2 p1 h2 d3
x7 s1 f1 a2 r1 k2 e1 p1 h2 d3

11. New Thinking
A multi-valued information system (MIS) is a
generalization of the idea of a single valued information
system (SIS).
Initiative two methods to:
Covert the SIS to a MIS and vice versa!
Covert the SDIS to a MDIS and vice versa!
by ( Collecting of Attributes).

12. Worked Example 2 (MDIS ):
Converted Data Description (MDIS)
Attribute Symbol ًRefers to ? ِAttribute Values ًRefers to ?
α1 S → s1
α2 K → k1
α {S,K}
α3 {S,K}→ {s2,k2}
β1 F → f1
β2 A →a1
β3 A →a2
β {F,A,E} β4 E → e1
β5 {F,A,E} →{f2,a0,e2}
δ1 R → r1
δ2 P→p1
δ {R,P,H} δ3 H→h1
δ4 {R,P,H}→
{r2,p2,h2}
d1 Rheumatic arthritis
d2 Rheumatic carditis
D Diagnosis Rheumatic arthritis
d3 and carditis

13. Worked Example 3 (MDIS ):
Rheumatic Fever MDIS Data
α β δ D
x1 {α2} {β1,β2,β4} {δ1,δ2,} {d3 }
x2 {α1,α2} {β1, β2,} {δ1,δ2,δ3} {d3 }
x3 {α3} {β1, β2, β4} {δ1,δ2} {d3 }
x4 {α1} {β1,β2,β4} {δ2 } {d1 }
x5 {α1} {β4} {δ1 } {d2 }
x6 {α1} {β1,β2} {δ1,δ2} {d3 }
x7 {α1} {β1, β3, β4} {δ1,δ2,δ3} {d3 }

14. Generalized Multi-
Valued Decision
Information System
(GMDIS)

15. Initiated a New Approach
 Initiate a new approach for data reduction in Generalized Multi–
Valued Decision Information System (GMDIS).
 Convert the SDIS to GMDIS.
 Two general relations are defined on condition attributes and
decision attribute.
 Construct new classes using the general relations which are used
for data reduction.
 Study The measure of decision dependency on the condition
attributes
 Evaluate the performance of the approach,
 an application of, rheumatic fever datasets has been chosen
and the reduct approach have been applied to see their
ability and accuracy.

16. Generalized Multi-valued
Decision Information System
A Generalized Multi-valued Information System can be defined as
follows.
(1) GMIS = (U , At , {y a : a  At}, fa , {h B : B  At})
A Generalized Multi-valued Decision Information System can be
defined as follows.
(2) GMDIS = (U , At U D , {y : a  At}, f , {h : B  At})
a a B

17. Set Approximations in GMDIS (1)
(1) hB = {(x, y) : fa ( x)c  fa (y) , "a  B , B  At}
(2) hB = {(x, y) : fa ( y)  fa ( x), "a  B , B  At}
(3) h = {( x , y ) : f ( x ) depends on f ( y )}
D D
D
= {( x , y ) : f ( x )  f ( y )}
D D
Define the set of all intersections of members of as the Meeting Point Relation (MPR) can be written as:
(4) m = {m = A I A , m  U A , A , A , A  A , i  j }
a l i j l ha
k k i j k

18. Set Approximations in GMDIS (2)
D
(5) POS B (D ) = U X h B
, B  At
X  Ah
D
Where, for any subset X  U the lower and
upper approximations are defined by,
X h
= U {h : h Bx  X }, B  At
Bx
(6) B
X h = U {h : h Bx I X  F }, B  At
B Bx

19. Suggested New Technique :
Consideration (1)
1.The set of attributes B  At is called a
reduct if t B  t D and B is minimal, where
t B  t D iff " G  t B , $G ' t D s.t. G  G ' , G , G ' U
2.The attribute a  At is called the principal
attribute (PA) if , ta f tb , "a, b At b  a and
,
if ta tb then both a and b are principal
=
attributes.

20. Suggested New Technique :
Consideration (2)
3. The set of attributes of equal highest degree
of dependency is the PA of the GMDIS.
If the set of all reducts of any SDIS is ,
Y = { R1 , R2 , L , Rn , and the set of reducts for the
}
GMDIS system using tha new approach is,
. Y' = { R1 ', R2 ', L, Rn '}.Then, it can be said that Y’
is more refinement than, Y if . " 'Y, $ Ys.t. R'R
R ' R
i i i i

21. Simplified Reducts
Is the set of all reducts, after omitted
the supersets of each reduct in the set
RED (At), and we denote it by SRED (At).

22. GMDIS Reduction Algorithms
 Algorithm 1: GMDIS Reduct
 Algorithm 2: GMDIS PA Algorithm

23. GMDIS Reduction Algorithms:
GMDIS Reduct
A GMDIS = (U , At U D ,{y a : a  At}, fa ,{hB : B  At})
(1) R  {}
(2) Do  R U { a}
(6) GMDIS
(3) GMDIS  R (7) R  GMDIS
(4) Loop a  ( At - R ) (8) Until tR tD
(5) If t R U{ a }  t D (9) Return R
R : A set of minimum attribute subset; R  At
Where R  Reduct

24. GMDIS Reduction Algorithms:
GMDIS PA Algorithm
A GMDIS = (U , At U D , {y a : a  At }, f a , {h B : B  At })
(1) PA  {} (6) PA  PA U { a}
(2) Do (7) End Loop
(3) Loop a  At (8) End Loop
(4) Loop b  At (9) Return PA
(5) If t a f t b
PA: A set of principal attribute subset, PA  At

25. Rheumatic Fever GMDIS Reduction:
Worked Example
Applying the new approach on MDIS Rheumatic
Fever data to be a GMDIS by using the relation
h B = {( x , y ) : f a ( x ) c  f a ( y ) , "a  B , B  At }
So we conclude that {a} is the reduct and it is the PA
of the GMDIS and this is the same result obtained
using the second consideration.
RED( At ) = {a } = { S , K }

26. Discernibility Matrix versus GMDIS
x1 x2 x3 x4 x5 x6 x7
x1 Ф
x2 Ф Ф
x3 Ф Ф Ф
x4 {S,R,K} {R,K,E,H} {S,A,R} Ф
{F,A,K,E,
x5 {S,F,A,K,P}
P,H}
{S,F,A,P} {F,A,R,P} Ф
x6 Ф Ф Ф {R,E} {F,A,E,P} Ф
x7 Ф Ф Ф {A,R,H} {F,A,P,H} Ф Ф
Rheumatic Fever Data Discernibility Matrix

27. The discernibility function
f = { S  R  K }  { R  K  E  H}  { S  A  R}  { S  F  A  K  P}
At
 { F  A  K  E  P  H}  { S  F  A  P}  { F  A  R  K  P}  { R  E}
 { F  A  E  P}  { A  R  H}  { F  A  P  H}
Re d ( At) = {{ S  R  K }, { S  A  R}, { S  F  A  P}, { F  A  R  K  P}, { R  E}
,{ F  A  E  P}, { A  R  H}, { F  A  P  H}}
RED ( At ) = {a } = { S , K }

28. Conclusion (1)
Reducts obtained by GMDIS is contained in the
reducts obtained on SDIS using the discernibility
matrix, that means that the new approach gives
more reduction.

29. Conclusion (2)
New approach for data reduction in GMDIS is considered
as a generalization in the case of MDIS.
This approach extended to Pawlak approach if the system
is single-valued and the relations are equivalence.
It Opens the way for other approaches of data reduction
if we use the general topological recent concepts such as
Pre-open sets, Semi-open sets, etc.

30. Conclusion (3)
In many real life situations, the use of attributes in a
single fashion is not represetable for the actual effect of
attributes. So, it is necessary to consider subsets of the
attributes as a multi criteria.
An application of, Rheumatic Fever datasets has been
chosen and the reduct approach has been applied to see
their ability and accuracy.

31. Acknowledgment
 The authors greatly appreciate and thanks many
peoples for their valuable comments and advices:
 Dr. K. E. Sturtz, , Air Force Research
Laboratory, Wright Patterson Air Force Base,
Ohio;
 Prof. Aboul Ella Hassanien, Cairo University
 Prof. E. Rady,, I.S.S.R., Cairo University.
 Dr. A. S. Salama. Pure Mathematics Dept.,
Faculty of Science, Tanta University.