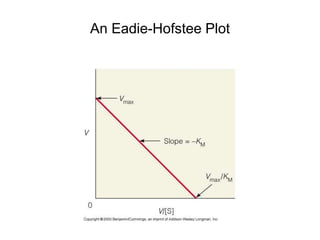
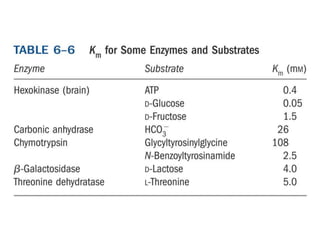
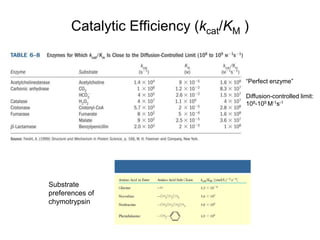
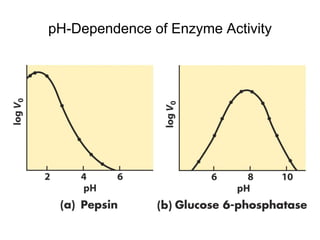
Enzymes catalyze biochemical reactions with great specificity and efficiency under mild conditions. Enzyme kinetics follows defined rate laws that can be modeled using Michaelis-Menten equations. The Michaelis-Menten equation relates reaction velocity to substrate concentration and defines kinetic parameters like Vmax and KM. Reaction rates are influenced by factors like temperature, pH, and the presence of inhibitors or activators. Different types of inhibition - competitive, uncompetitive, mixed - affect kinetic parameters in characteristic ways. Irreversible inhibitors permanently inactivate the enzyme through covalent modification.

1. Enzyme Kinetics

2. Enzymes Are Uniquely Powerful Catalysts
• Enzymes are proteins that can accelerate
biochemical reactions by factors of 105 to 1017!
This is much higher than chemical catalysts.
• Enzymes can be extremely specific in terms of
reaction substrates and products.
• Enzymes catalyze reactions under mild
conditions (e.g., pH 7.4, 37ºC).
• The catalytic activities of many enzymes can be
regulated by allosteric effectors.

3. Chemical Kinetics

4. Irreversible First-Order Reactions
A  B
v = d[B]/dt = -d[A]/dt = k[A]
(k = first-order rate constant (s-1))
Change in [A] with time (t):
[A]= [A]o e –kt or
[A]/[A]o = e –kt
ln([A]/[A]o) = –kt
([A]o = initial concentration)
k

5. Reversible First-Order Reactions
A B
v = -d[A]/dt = k1[A] - k-1[B]
At equilibrium: k1[A]eq - k-1[B]eq = 0
[B]eq/[A]eq = k1/k-1 = Keq
k1
k-1



6. Second-Order Reactions
2A  P
v = -d[A]/dt = k[A]2
Change in [A] with time:
1/[A] = 1/[A]o + kt
A + B  P
v = -d[A]/dt = -d[B]/dt = k[A][B]
(k = second-order rate constant (M-1s-1))
k
k
Note: third-order reactions rare, fourth- and higher-order reactions unknown.

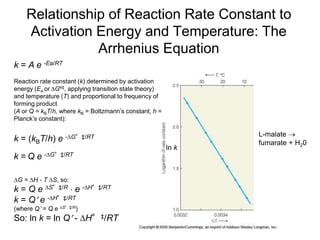
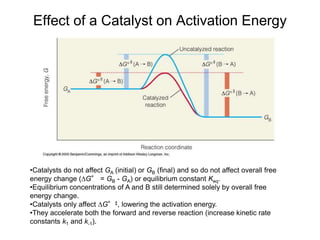
7. Free Energy Diagrams
Keq = e –∆Gº/RT
For A A‡
[A]‡/[A]o = e –∆Gº‡/RT
[A]‡ = [A]o e –∆Gº‡/RT
Keq = equilibrium constant
[A]‡ = concentration of molecules having the activation energy
[A]o = total concentration of A
–∆Gº‡ = standard free energy change of activation (activation energy)



8. Relationship of Reaction Rate Constant to
Activation Energy and Temperature: The
Arrhenius Equation
k = A e -Ea/RT
Reaction rate constant (k) determined by activation
energy (Ea or ∆Gº‡, applying transition state theory)
and temperature (T) and proportional to frequency of
forming product
(A or Q = kBT/h, where kB = Boltzmann’s constant, h =
Planck’s constant):
k = (kBT/h) e -G°‡/RT
k = Q e -G°‡/RT
G = H - T S, so:
k = Q e S°‡/R  e -H°‡/RT
k = Q e -H°‡/RT
(where Q = Q e S°‡/R)
So: ln k = ln Q - H°‡/RT
L-malate 
fumarate + H20
ln k

9. Relation of Equilibrium Constant to
Activation Energy
Keq = k1/k-1
Keq = (Q e -G1°‡/RT)/(Q e -G-1°‡/RT)
Keq = e -(G1°‡ - G-1°‡)/RT
∆G° = G1°‡ - G-1°‡
Keq = e –∆G°/RT
Equilibrium constant Keq says nothing about rate of
reaction, only free energy difference between final and
initial states. The activation energy barrier opposes
reaction in both directions

10. Effect of a Catalyst on Activation Energy
•Catalysts do not affect GA (initial) or GB (final) and so do not affect overall free
energy change (∆G° = GB - GA) or equilibrium constant Keq.
•Equilibrium concentrations of A and B still determined solely by overall free
energy change.
•Catalysts only affect ∆G°‡, lowering the activation energy.
•They accelerate both the forward and reverse reaction (increase kinetic rate
constants k1 and k-1).

11. Intermediate States in Multistep
Reactions

12. Enzyme Kinetics

13. The Effect of Substrate Concentration on
Reaction Velocity

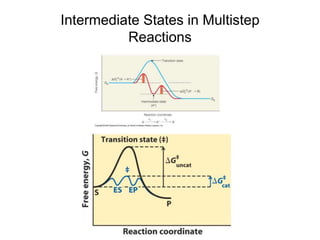
14. Michaelis-Menten Kinetics (1)
v = k2[ES]
(Note: k2 also referred to as kcat)
[Enzyme]total = [E]t = [E] + [ES]
How to solve for [ES]?
1. Assume equilibrium, if k-1 >> k2:
KS = k-1/k1 = [E][S]/[ES]
or
2. Assume steady state:
d[ES]/dt = 0
(Michaelis and
Menten, 1913)
(Briggs and
Haldane, 1925)
E = enzyme, S = substrate,
ES = enzyme-substrate complex,
P = product

15. The Steady State in Enzyme Kinetics

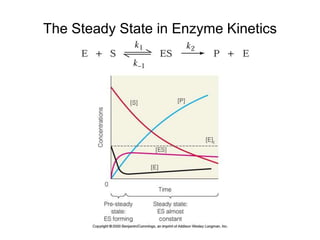
16. Michaelis-Menten Kinetics Continued (2)
Rate of formation of ES complex = k1[E][S]
Rate of breakdown of ES complex = k-1[ES] + k2[ES]
Because of steady state assumption:
k1[E][S] = k-1[ES] + k2[ES]
Rearranging: [ES] = (k1/(k-1 + k2))[E][S]
Substituting Michaelis constant = KM = (k-1 + k2)/k1) = KS + k2/k1:
[ES] = ([E][S])/KM
So: KM[ES] = [E][S]

17. Michaelis-Menten Kinetics Continued (3)
Substituting [E] = [E]t - [ES]:
KM[ES] = [E]t[S] - [ES][S]
Rearranging: [ES](KM + [S]) = [E]t[S]
So: [ES] = [E]t[S]/(KM + [S])

18. Michaelis-Menten Kinetics Continued (4)
Now we can substitute for [ES] in the rate equation
vo = k2[ES].
But first note that the velocity in v = k2[ES] we use is the initial
velocity, vo, the velocity of the reaction after the pre-steady state
and in the early part of the steady state, i.e., before ~10% of
substrate is converted to product. This is because at this stage of
the reaction, the steady-state assumption is reasonable ([ES] is still
approximately constant). Also, since not much P has yet
accumulated, we can approximate the kinetics for even reversible
reactions with this equation if we limit ourselves to vo.

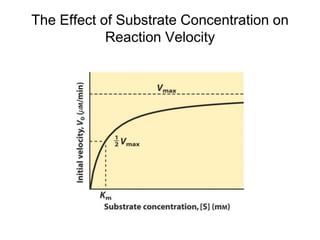
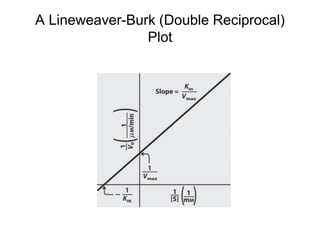
19. The Michaelis-Menten Equation
vo = k2[E]t[S]/(KM + [S])
or
vo = Vmax[S]/(KM + [S])
(since Vmax = k2[E]t when [S] >> KM)

20. A Lineweaver-Burk (Double Reciprocal)
Plot

21. An Eadie-Hofstee Plot

22. Multistep Reactions
E + S ES  ES  E + P
vo = kcat[E]t[S]/(KM + [S])
k2 k3
k1
k-1


kcat = empirical rate constant that reflects rate-
determining component. Mathematically, for the
reaction above,
kcat = k2k3/(k2 + k3).
However, k2 and k3 often very hard to establish
with precision as individual rate constants.

26. Catalytic Efficiency (kcat/KM )
“Perfect enzyme”
Diffusion-controlled limit:
108-109 M-1s-1
Substrate
preferences of
chymotrypsin

27. pH-Dependence of Enzyme Activity

28. Enzyme-Catalyzed Bisubstrate Reactions:
Two Examples

29. Bisubstrate Reactions
S1 + S2 P1 + P2
A-X + B A + B-X (in transferase reactions)
• Sequential binding of S1 and S2 before catalysis:
– Random substrate binding - Either S1 or S2 can
bind first, then the other binds.
– Ordered substrate binding - S1 must bind before
S2.
• Ping Pong reaction - first S1  P1, P1 released
before S2 binds, then S2  P2.
E


E



30. Ping Pong reaction
Sequential binding
Ternary
complex

31. Indicative of ternary complex formation and a sequential
mechanism

32. Indicative of a Ping Pong mechanism

33. Enzyme Inhibition

34. Types of Enzyme Inhibition
• Reversible inhibition
(Inhibitors that can reversibly bind and dissociate from
enzyme; activity of enzyme recovers when inhibitor diluted
out; usually non-covalent interaction.)
– Competitive
– Mixed (noncompetitive)
– Uncompetitive
• Irreversible inhibition
(Inactivators that irreversibly associate with enzyme; activity
of enzyme does not recover with dilution; usually covalent
interaction.)

35. Competitive Inhibition

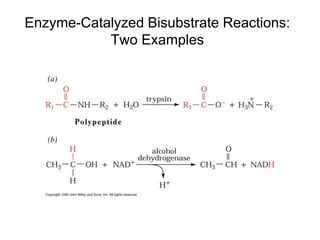
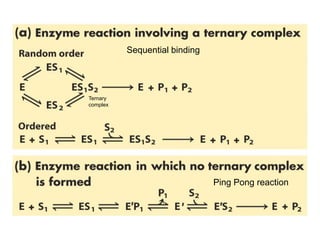
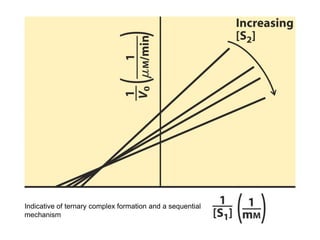
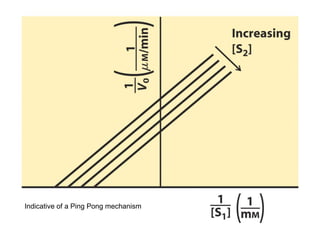
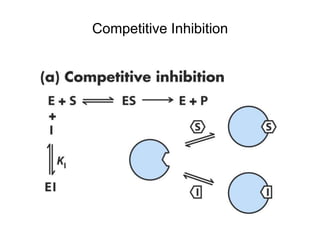
36. Effects of Competitive Inhibitor on
Enzyme Kinetics
Kapp
M = KM(1 + [I]/KI) > KM
Vapp
max = Vmax
KI (inhibitor dissociation
constant) = koff/kon

37. a = 1 + [I]/KI

38. A Substrate and Its Competitive Inhibitor

39. HIV Protease Inhibitors

40. Relationship of KI to Half-Maximal
Inhibitory Concentration (IC50)
For a competitive inhibitor of an enzyme that follows
Michaelis-Menton kinetics:
vI/v0 = (Vmax[S]/(KMa + [S]))/(Vmax[S]/(KM + [S])) = (KM +
[S])/(KMa + [S])
vI = initial velocity with inhibitor
v0 = initial velocity without inhibitor
a = 1 + [I]/KI
When vI/v0 = 0.5, [I] = IC50 = KI(1 + [S]/KM)
If measurement made when [S] << KM, IC50 = KI

41. Uncompetitive Inhibition

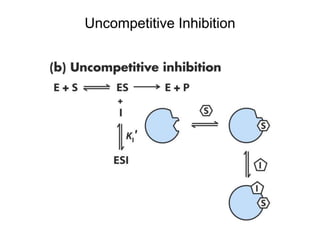
42. Effects of Uncompetitive Inhibitor on
Enzyme Kinetics
Kapp
M = KM/(1 + [I]/KI) < KM
Vapp
max = Vmax/(1 + [I]/KI) < Vmax

43. a = 1 + [I]/KI

44. Mixed (Noncompetitive) Inhibition

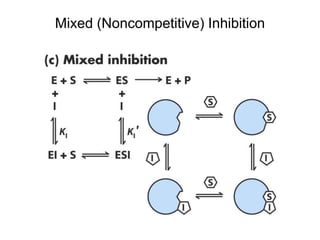
45. Effects of Mixed (Noncompetitive)
Inhibitor on Enzyme Kinetics
Kapp
M = (1 + [I]/KI)KM/(1 + [I]/KI)
(= KM, when KI = KI, which is often the case.)
Vapp
max = Vmax/(1 + [I]/KI) < Vmax
k1


k-1
•Not the same as uncompetitive inhibition.
•In mixed inhibition, inhibitor can bind E or
ES.

46. a = 1 + [I]/KI
a = 1 + [I]/KI

47. a = 1 + [I]/KI
a = 1 + [I]/KI
(For mixed inhibitor,
generally, ~ KM)

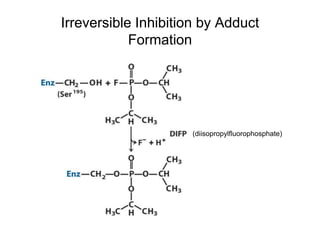
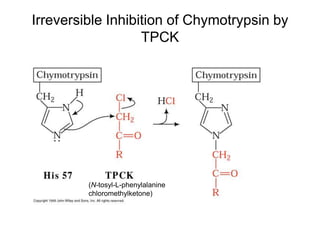
48. Irreversible Inhibition
k1


k-1
k2
E + I E·I  E-I
Plot:
ln(residual enzyme activity) vs. time
If [I]>>[E], conditions are pseudo-first
order and slope is -kobs (pseudo-first
order inactivation rate constant)
kinact (second-order inactivation constant)
= k1k2/k-1 = kobs/[I]
Slope = -kobs

49. Irreversible Inhibition by Adduct
Formation
(diisopropylfluorophosphate)

50. Irreversible Inhibition of Chymotrypsin by
TPCK
(N-tosyl-L-phenylalanine
chloromethylketone)