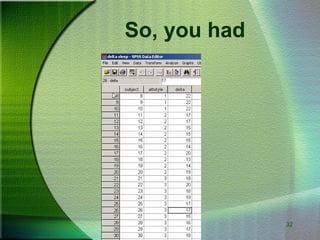
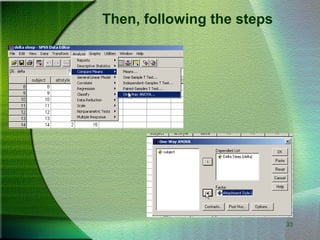
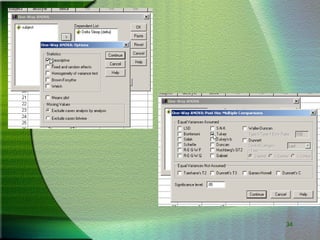
This document provides an overview of one-way analysis of variance (ANOVA), including definitions, assumptions, calculations, examples, and limitations. ANOVA allows researchers to determine if variability between groups is greater than expected by chance. The document explains how to calculate sums of squares, F-ratios, and p-values to test the null hypothesis that means are equal across groups.

1. 1
Basic Concepts of One-way
Analysis of Variance
(ANOVA)
Sporiš Goran, PhD.
http://kif.hr/predmet/mki
http://www.science4performance.com/

2. 2
Overview
• What is ANOVA?
• When is it useful?
• How does it work?
• Some Examples
• Limitations
• Conclusions

3. 3
Definitions
• ANOVA: analysis of variation in an
experimental outcome and
especially of a statistical variance in
order to determine the contributions
of given factors or variables to the
variance.
• Remember: Variance: the square of
the standard deviation
Remember: RA
Fischer, 1919-
Evolutionary Biology

4. 4
Introduction
• Any data set has variability
• Variability exists within groups…
• and between groups
• Question that ANOVA allows us to
answer : Is this variability significant, or
merely by chance?

5. 5
• The difference between variation
within a group and variation
between groups may help us
determine this. If both are equal it is
likely that it is due to chance and
not significant.
• H0: Variability w/i groups =
variability b/t groups, this means
that 1 = n
• Ha: Variability w/i groups does not =
variability b/t groups, or, 1 ≠ n

6. 6
Assumptions
• Normal distribution
• Variances of dependent
variable are equal in all
populations
• Random samples; independent
scores

7. 7
One-Way ANOVA
• One factor (manipulated
variable)
• One response variable
• Two or more groups to
compare

8. 8
Usefulness
• Similar to t-test
• More versatile than t-test
• Compare one parameter
(response variable) between
two or more groups

9. 9
For instance, ANOVA
Could be Used to:
• Compare heights of plants with and
without galls
• Compare birth weights of deer in
different geographical regions
• Compare responses of patients to
real medication vs. placebo
• Compare attention spans of
undergraduate students in different
programs at PC.

10. 10
Why Not Just Use t-
tests?
• Tedious when many groups are
present
• Using all data increases
stability
• Large number of
comparisons some may
appear significant by chance

11. 11
Remember that…
• Standard deviation (s)
n
s = √[(Σ (xi
– X)2
)/(n-1)]
i = 1
• In this case: Degrees of freedom (df)
df = Number of observations or groups - 1

12. 12
Notation
• k = # of groups
• n = # observations in each group
• xij = one observation in group i
• Y = mean over all groups
• Yi = mean for group i
• SS = Sum of Squares
• MS = Mean of Squares
• λ = Between MS/Within MS

13. 13
FYI this is how SS
Values are calculated
k ni
• Total SS = Σ Σ (xij
– )2 =
SStot
i=1 j=1
k ni
• Within SS = Σ Σ (xij
– i
)2 =
SSw
i=1 j=1
k ni
• Between SS = Σ Σ ( i
– )2 =
SSbet
i=1 j=1

14. 14
and
• SStot = SSw + SSbet

15. 15
Calculating MS Values
• MS = SS/df
• For between groups, df = k-1
• For within groups, df= n-k

16. 16
Hypothesis Testing &
Significance Levels

17. 17
F-Ratio = MSBet/MSw
• If:
– The ratio of Between-Groups MS:
Within-Groups MS is LARGE reject
H0 there is a difference between
groups
– The ratio of Between-Groups MS:
Within-Groups MS is SMALLdo not
reject H0 there is no difference
between groups

18. 18
p-values
• Use table in stats book to determine
p
• Use df for numerator and
denominator
• Choose level of significance
• If F > critical value, reject the null
hypothesis (for one-tail test)

19. 19
Example 1, pp. 400 of
your handout
• Three groups:
– Middle class sample
– Persons on welfare
– Lower-middle class sample
• Question: Are attitudes toward
welfare payments the same?

20. 20
So,

21. 21
and
From the table with  = 0.05 and df = 2 and 24, we see that if
F > 3.40 we can reject Ho. This is what we would conclude
in this case.

22. 22
Example 2
• Bat cave gates:
– Group 1 = No gate (NG)
– Group 2 = Straight entrance gate (SE)
– Group 3 = Angled entrance gate (AE)
– Group 4 = Straight dark zone gate (SD)
– Group 5 = Angled dark zone gate (AD)
• Question: Is variation in bat flight
speed greater within or between
groups? Or Ho = no difference
significant difference in means.

23. 23
Just leave me alone
Max! Go back to
your hockey!

24. 24
Example 2 (cont’d)
Group #,
i
Gate
Type
Mean FS (m/s) sd FS (m/s) ni
1 NG 5.6 0.93 150
2 SE 3.8 1.05 150
3 AE 4.7 0.97 150
4 SD 4.2 1.23 137
5 AD 5.1 1.03 143
Hypothetical data for bat flight speed with various gate arrangements.
FS= Flight speed; sd = standard deviation

25. 25
Example 2  SSbet
Between SS = 300
Group
#, i
Gate
Type
Mean FS
(m/s)
sd FS (m/s) ni
1 NG 5.6 0.93 150
2 SE 3.8 1.05 150
3 AE 4.7 0.97 150
4 SD 4.2 1.23 137
5 AD 5.1 1.03 143

26. 26
Example 2  SSw
Within SS = 790
Group
#, i
Gate
Type
Mean FS
(m/s)
sd FS (m/s) ni
1 NG 5.6 0.93 150
2 SE 3.8 1.05 150
3 AE 4.7 0.97 150
4 SD 4.2 1.23 137
5 AD 5.1 1.03 143

27. 27
Example 2 (cont’d)
• Between MS = 300/4 = 75
• Within MS = 790/(730-5) = 1.09
• F Ratio = 75/1.09 = 68.8
• See Table find p-value based on
df= 4,
• Since F>value found on the table we
reject Ho.

28. 28
What ANOVA Cannot
Do
• Tell which groups are different
– Post-hoc test of mean differences
required
• Compare multiple parameters
for multiple groups (so it
cannot be used for multiple
response variables)

29. 29
Some Variations
• Two-Way, Three-Way, etc.
ANOVA (will talk about this next
class)
– 2+ factors
• MANOVA (Multiple analysis of
variance)
– multiple response variables

30. 30
Summary
• ANOVA:
– allows us to know if variability in a data
set is between groups or merely within
groups
– is more versatile than t-test
– can compare multiple groups at once
– cannot process multiple response
variables
– does not indicate which groups are
different

31. 31
Now, let’s go to our
SPSS manual
• Perform the sample problem on the effects
of attachment styles on the psychology of
sleep with the data set from the NAAGE
site called Delta Sleep.
• Pay attention to the procedure and the
post-hoc tests to determine which groups
are significantly different. Perform the
Tukey Test at a 5% significance level.
• Look at your output and interpret your
results.
• Tell me when you are done.

32. 32
So, you had

33. 33
Then, following the steps

34. 34

35. 35
You got

36. 36
and

37. 37
What do all these
mean?

38. 38
When you are done
with this,
• Do practice exercises 1, 4, 6, 7
and 12 from the handout in
SPSS.
– Create the data sets.
– Run the one-way ANOVAS and
interpret your results.