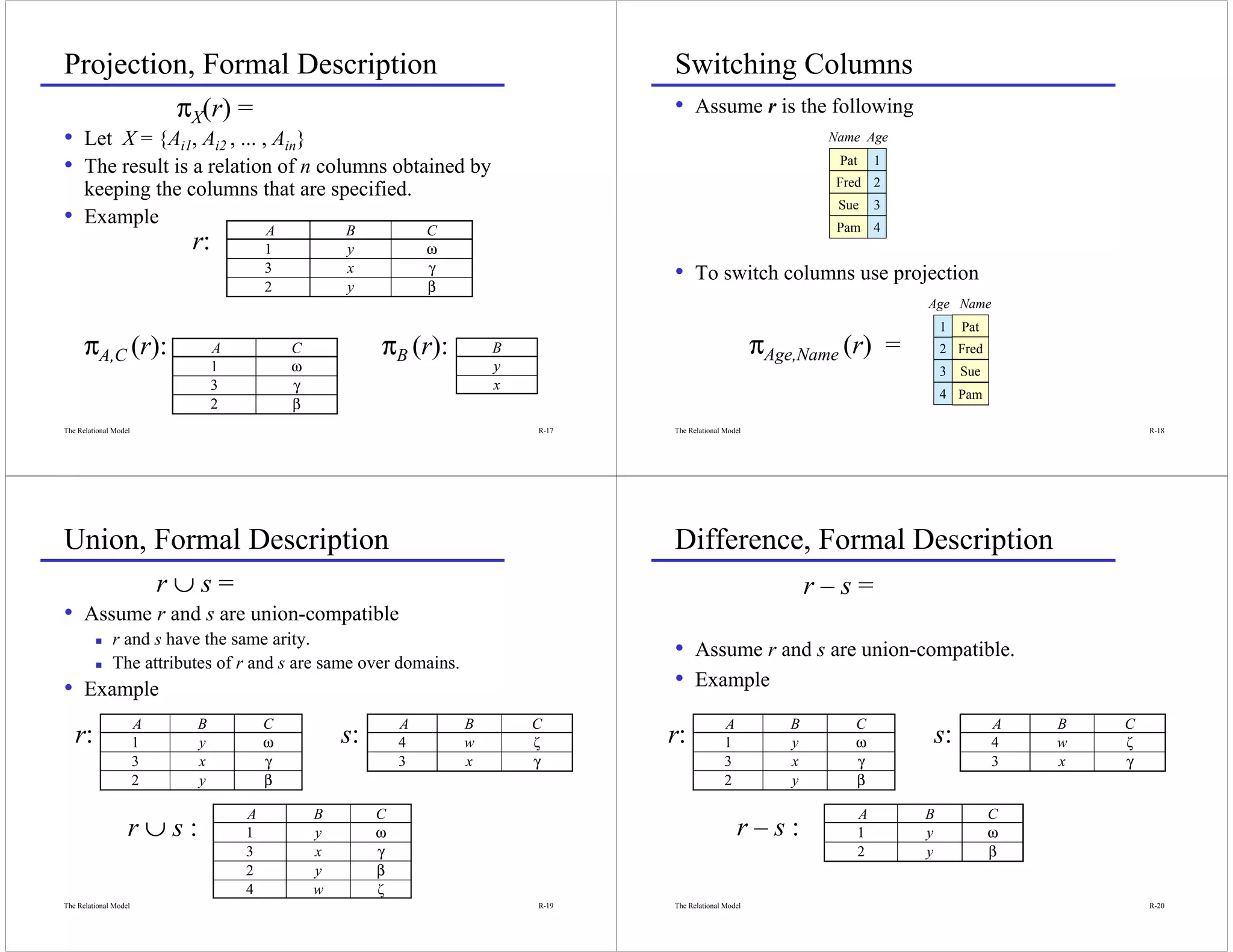
The document summarizes the relational model, which represents data as mathematical relations - tables with rows and columns. It describes key concepts like relations, tuples, domains, attributes, and relational algebra operations like selection, projection, join, union and difference. Relational algebra provides a way to manipulate relations through a set of basic operations. However, relational algebra has some limitations like not supporting aggregates, missing data, sorting, or modifying the database.


![Tuples Characteristics of Relations
Definition: An element t of a relation r is called a tuple. • Tuples in a relation are unorderd.
• Example: The following two relations have the same
• We refer to component values of a tuple t by t[Ai] = vi information content.
(the value of attribute Ai for tuple t).
Alternatively, use ‘dot’ notation, e.g., t.Ai is the ith attribute
of tuple t
Name Age Name Age
• t[Ai, ... , Ak] refers to the subtuple of t containing the
Pat 1 Sue 3
values of attributes Ai, ... , Ak respectively. Fred 2 Pam 4
• Table metaphor Sue 3 Fred 2
Tuple is a row Pam 4 Pat 1
Attribute is a column
The Relational Model R-9 The Relational Model R-10
Characteristics of Relations (cont.) Characteristics of Relations (cont.)
• Attributes in a tuple/relation are ordered. • Values in a tuple are atomic (indivisible).
But, we can change the order at will (to be shown in future). • A value cannot be a structure, record, or relation
Example: The following relations do not have the same Example: All atomic values (string or integer).
information. Name Age
Pat 1
Name Age Age Name Fred 2
Pat 1 1 Pat
Fred 2 2 Fred Example: The following is not a relation, Name is not atomic
Sue 3 3 Sue Name Age
Pam 4 4 Pam First Last
1
Joe Doe
First Last
2
Sue Doe
The Relational Model R-11 The Relational Model R-12](https://image.slidesharecdn.com/2redreviewrelation-120513212308-phpapp01/75/2red-reviewrelation-3-2048.jpg)
![Degree and Cardinality Relational Algebra
Ord CID Date Salesperson
• Five primary operators (complete)
102 42 860207 Johnson Selection: σ
103 39 860211 Strong
Projection: π
104 24 860228 Boggs
105 42 860303 Strong Union: ∪
107 34 860308 West Tuples (or records, rows)
108 46 860308 Wset
[Cardinality is # of them] Difference: –
110 24 860312 Boggs Cartesian Product: ×
111 21 860318 Strong
112 29 860320 Clark
• Convenient derived operators (closed)
degree/arity Intersection: ∩
Theta join nθ, equijoin n= , and natural join n
Semijoins: left l and right r
Relational division: ÷
The Relational Model R-13 The Relational Model R-14
RA Operations Produce Relations Selection, Formal Description
σP(r) =
• P is a formula in propositional calculus, dealing with terms of
Name Age Name Age Name the form:
joe 4 sue 10 sue
attribute (or constant) = attribute (or constant)
sue 10 sam 9 sam
sam 9 operation1 operation2 attribute ≠ attribute
attribute < attribute
attribute ≤ attribute
attribute ≥ attribute
attribute > attribute
Notation: operation2( operation1(R) ) term ∧ term (Note: ∧ is AND)
term ∨ term (Note: ∨ is OR)
¬(term)
The Relational Model R-15 The Relational Model R-16](https://image.slidesharecdn.com/2redreviewrelation-120513212308-phpapp01/75/2red-reviewrelation-4-2048.jpg)

![Natural Join Semijoins
r n s= r ls =
• Schema of result is R∪S • The result has the same schema as the left-hand
• Let t be a tuple in the result. argument, r.
t[R] has the same value as a tuple tR ∈ r. • Example
t[S] has the same value as a tuple ts ∈ s.
A B C
• Example r: 1 y ω
s: D
“Tom”
B
y
A B C
r: 1 y ω
s: D
“Tom”
B
y
3 x γ
2 y β
3 x γ “Eric” x
2 y β
rls: A B C
A B C D 1 y ω
rns: 1 y ω “Tom” 2 y β
3 x γ “Eric”
2 y β “Tom” • Right semijoin: r r s =
The Relational Model R-25 The Relational Model R-26
Relational Division Relational Division, cont.
r ÷ s = { t | ∀u ∈s (t u ∈ r)} • Let r and s be relations on schemes R and S
respectively, where
• Example
R = (A1, A2, ..., An, B1, B2, ..., Bn,)
A B C
S = (B1, B2, ..., Bn,)
B
r: 1 y ω
s: y
3 x γ z
2 y β • The result of r divided by s is a relation on scheme
1 z ω R ÷ S = (A1, A2, ..., An)
r÷s: A
1
C
ω
• R ÷ S = πR – S (r) – πR – S ((πR – S (r) × s) – r)
The Relational Model R-27 The Relational Model R-28](https://image.slidesharecdn.com/2redreviewrelation-120513212308-phpapp01/75/2red-reviewrelation-7-2048.jpg)
![Renaming Operator Limitations of the Algebra
• Find the film(s) with the highest rental price. • Can't do arithmetic.
Find the rental price assuming a 10% increase.
• We need a renaming operator: ρName • Can't do aggregates.
How many films has each customer reserved?
• Alternative formulation: Find the film(s) with a rental • Can't handle “missing” data.
price for which no other rental price is higher. Make a list of the films, along with who reserved it, if
applicable.
• Can't perform transitive closure.
For a partof(Part, ConstituentPart) relation, find all parts in
the car door.
πTitle(Film) –
πF2.Title (σFilm.RentalPrice > F2.RentalPrice (Film×ρF2(Film))) • Can't sort, or print in various formats.
Print a reserved summary, sorted by customer name.
• Can't modify the database.
Increase all $3.25 rentals to $3.50.
The Relational Model R-29 The Relational Model R-30
Extending the Projection Operator Aggregates
• The generalized projection operator allows expressions AGagg1, ..., aggk (r) =
in addition to column names in the subscript. t a1 ... ak | t ∈ r ∧
a1 = agg1 ({u | u ∈ r ∧ u[G] = t[G]})
• Find the rental price, assuming a 10% increase. ....
ak = aggk ({u | u ∈ r ∧ u[G] = t[G]})
πTitle, RentalPrice*1.1(Film) • Appends new attributes.
• Each aggregate function aggi decides which attribute
to aggregate over.
• The grouping attributes A are optional.
The Relational Model R-31 The Relational Model R-32](https://image.slidesharecdn.com/2redreviewrelation-120513212308-phpapp01/75/2red-reviewrelation-8-2048.jpg)

![Relational Calculus Relational Calculus, cont.
• The relational algebra is procedural, specifying a • Two forms of calculi
sequence of operations to derive the desired results.
• Relational calculus is based on first-order predicate
calculus.
• Relational calculus is more declarative, specifying Tuple Relational Calculus (TRC)
what is desired.
• The expressive power of the two languages is identical.
This implies that relational calculus is relationally complete. Domain Relational Calculus (DRC)
• Many commercial relational query languages are based
on the relational calculus.
• The implementations are based on the relational
algebra.
The Relational Model R-37 The Relational Model R-38
Tuple Relational Calculus Syntax of Tuple Relational Calculus
• A tuple variable ranges over tuples of a particular {t1 .A1, t2.A2, ... , tj.Aj | P (t1, t2 , ... , tj)}
relation.
• Example: List the information about expensive films.
• t1, t2 , ... , tj are tuple variables.
{t | t ∈ Film ∧ t[RentalPrice] > 4}
• t ∈ Film specifies the range relation Film for the tuple • Each tk is an tuple of the relation over which it ranges.
variable t.
• Each tuple satisfying t[RentalPrice] > 4 is retrieved.
• The entire tuple is retrieved.
• P is a predicate, which is made up of atoms, of the
following types.
• List the titles of expensive films.
tk ∈ R or R (tk) identifies R as the range of tk
{t | x ∈ Film (x[RentalPrice] = t[RentalPrice]
Atoms from predicate calculus: ∧, ∨, ¬,∀, ∃
∀
∧ x[RentalPrice] > 4)}
The Relational Model R-39 The Relational Model R-40](https://image.slidesharecdn.com/2redreviewrelation-120513212308-phpapp01/75/2red-reviewrelation-10-2048.jpg)

![Completeness Completeness, Example
• Theorem: The tuple relational calculus is complete. • List the titles of all reserved films.
πTitle (σFilm,FilmID = Reserved.FilmID(Film × Reserved))
πTitle (Film n Reserved)
• Proof:
Selection σP(r) ⇒ { t | t ∈ r ∧ P(t) }
Projection πX(r) ⇒ {t | s ∈ r (s[X] = t[X] )} • Replace projection:
Union r∪s⇒{t|t∈r∨t∈s}
Difference r – s ⇒ { t | t ∈ r ∧ ¬t ∈ s }
Cartesian product r×s⇒ {t q|t∈r∧ q∈s} {t.Title | t ∈ σFilm,FilmID = Reserved.FilmID
Induct on length of the algebraic expression. (Film × Reserved)}
The Relational Model R-45 The Relational Model R-46
Completeness, Example, Cont. Equivalence of Expressive Power
• Replace selection: • Theorem: The relational algebra is as expressive as the
(safe) tuple relational calculus.
{t.Title | t ∈ (Film × Reserved)
∧ t[Film.FilmID] = t[Reserved.FilmID] }
• (Informal) Proof: by induction on the number of
operators in the calculus predicate
• Replace the Cartesian product:
{t.Title. | q ∈ Film ∧ r ∈ Reserved
∧ q.FilmID = r.FilmID ∧ t = q r }
The Relational Model R-47 The Relational Model R-48](https://image.slidesharecdn.com/2redreviewrelation-120513212308-phpapp01/75/2red-reviewrelation-12-2048.jpg)