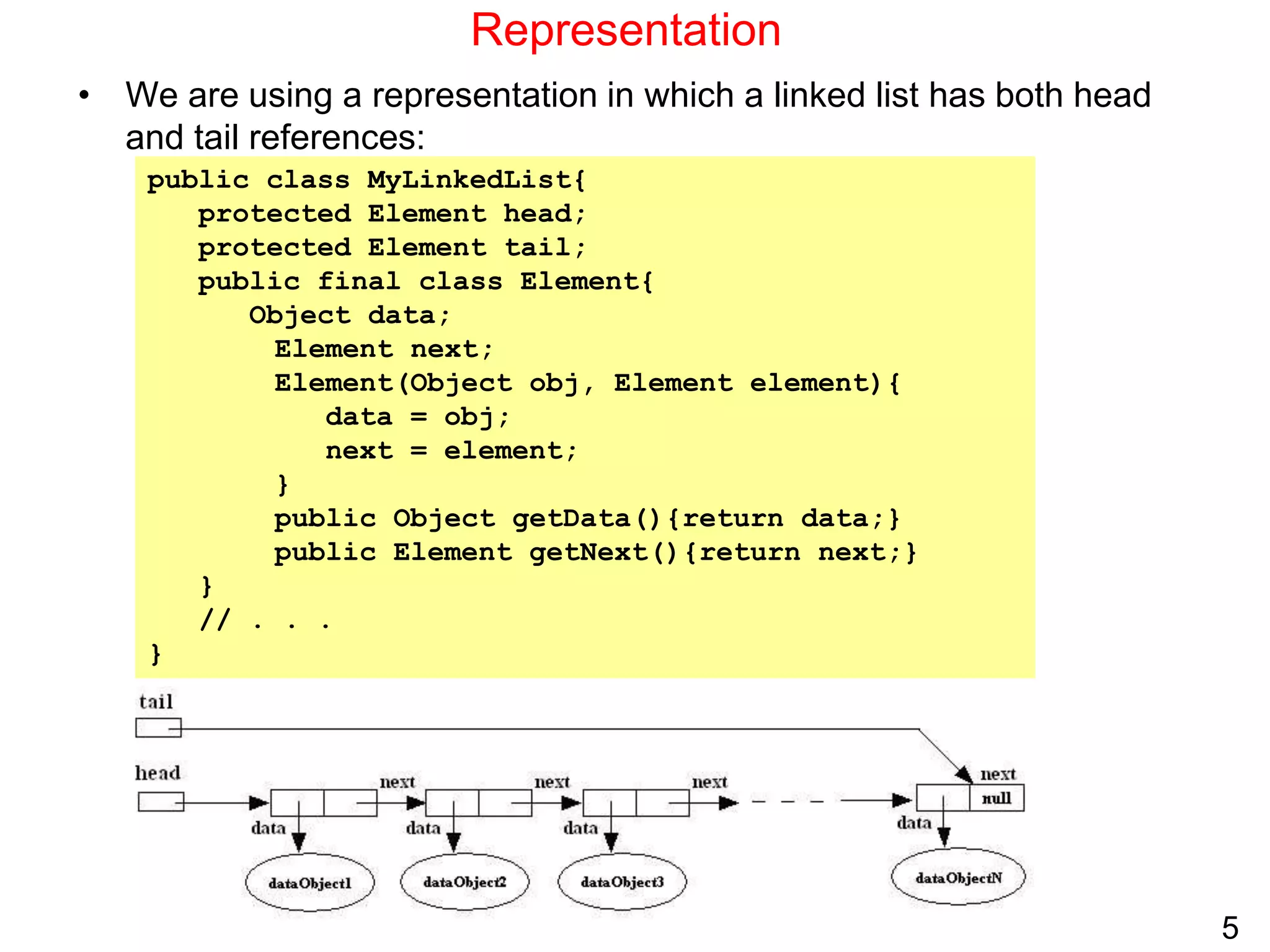
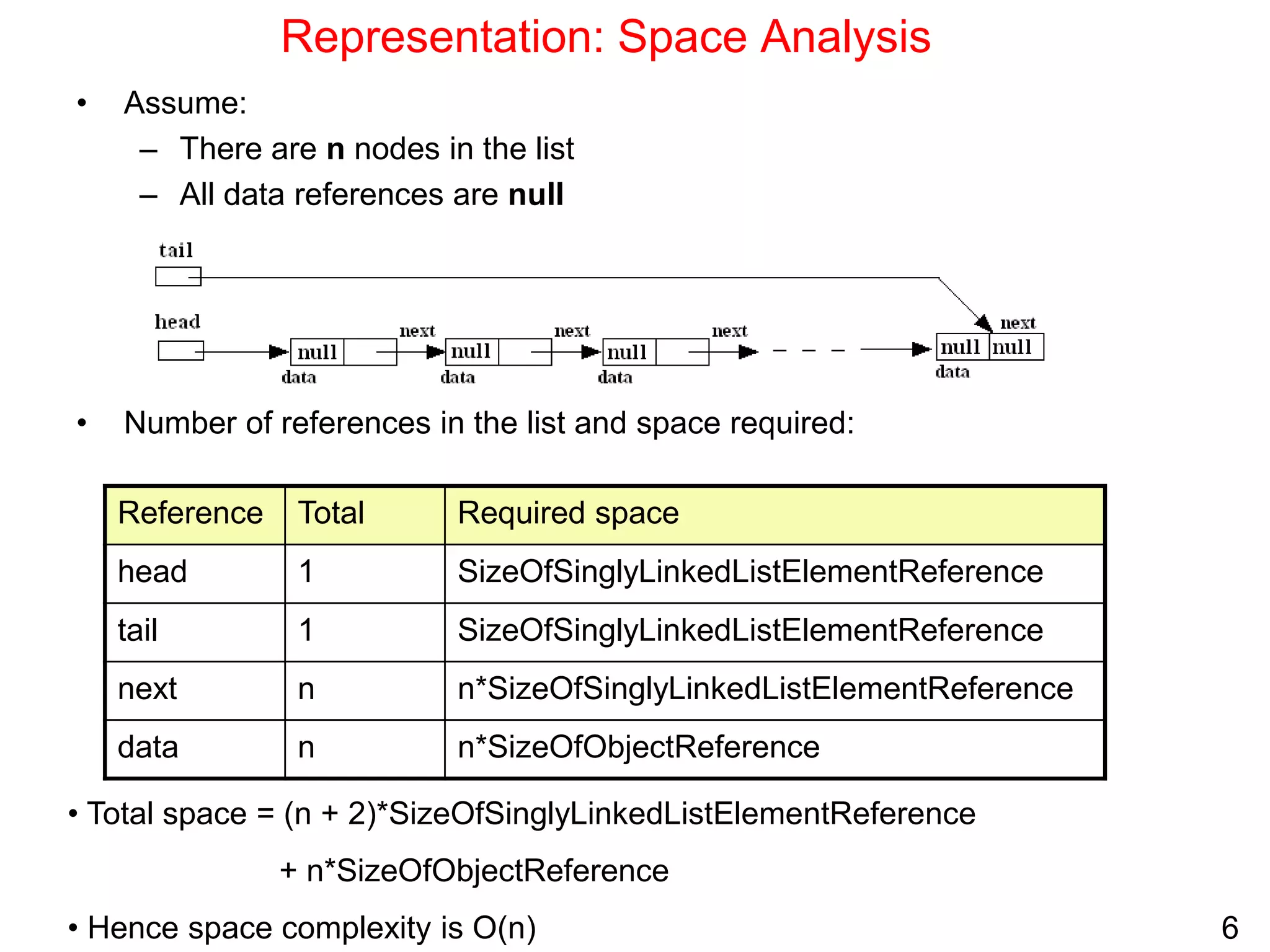
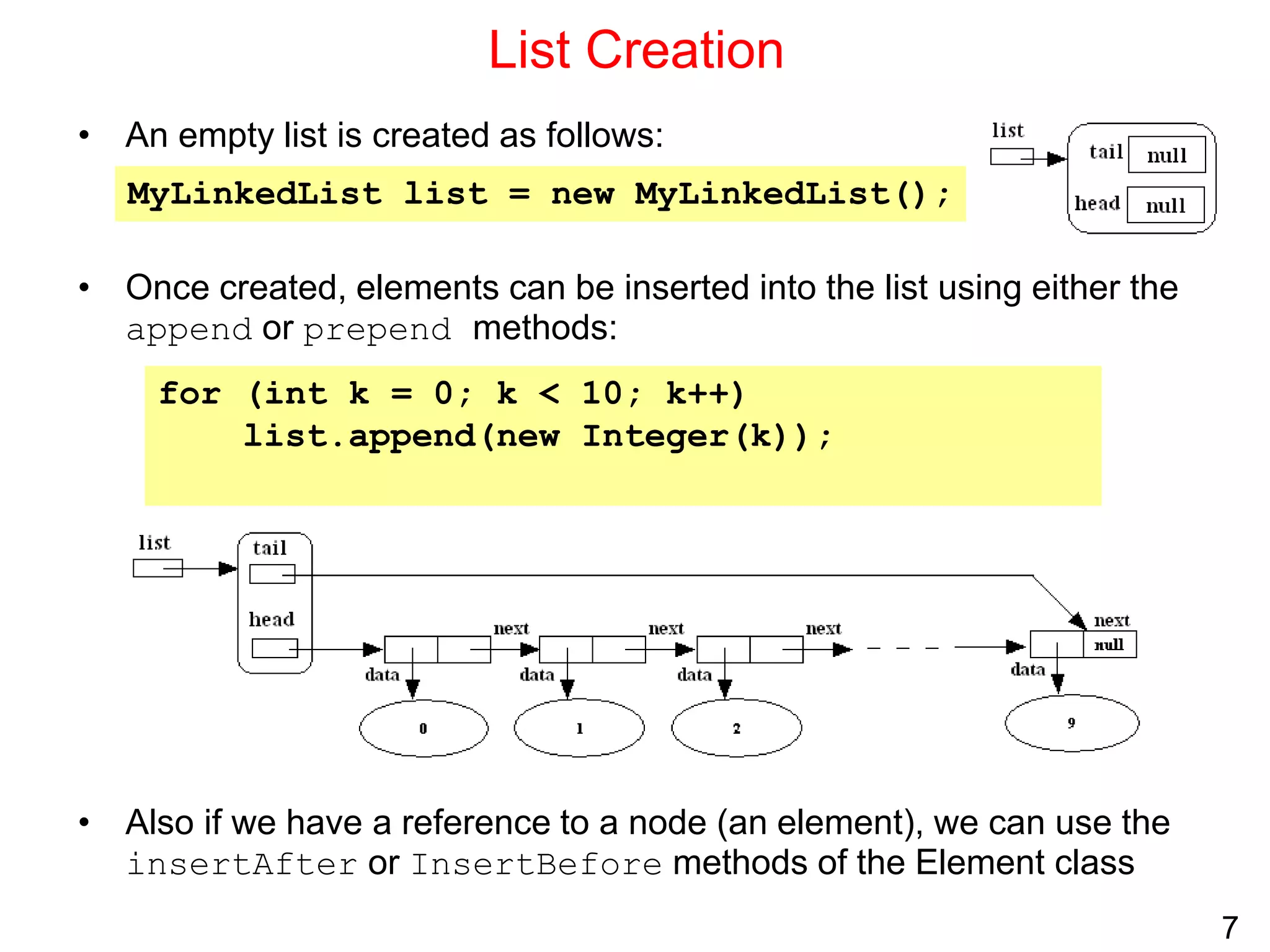
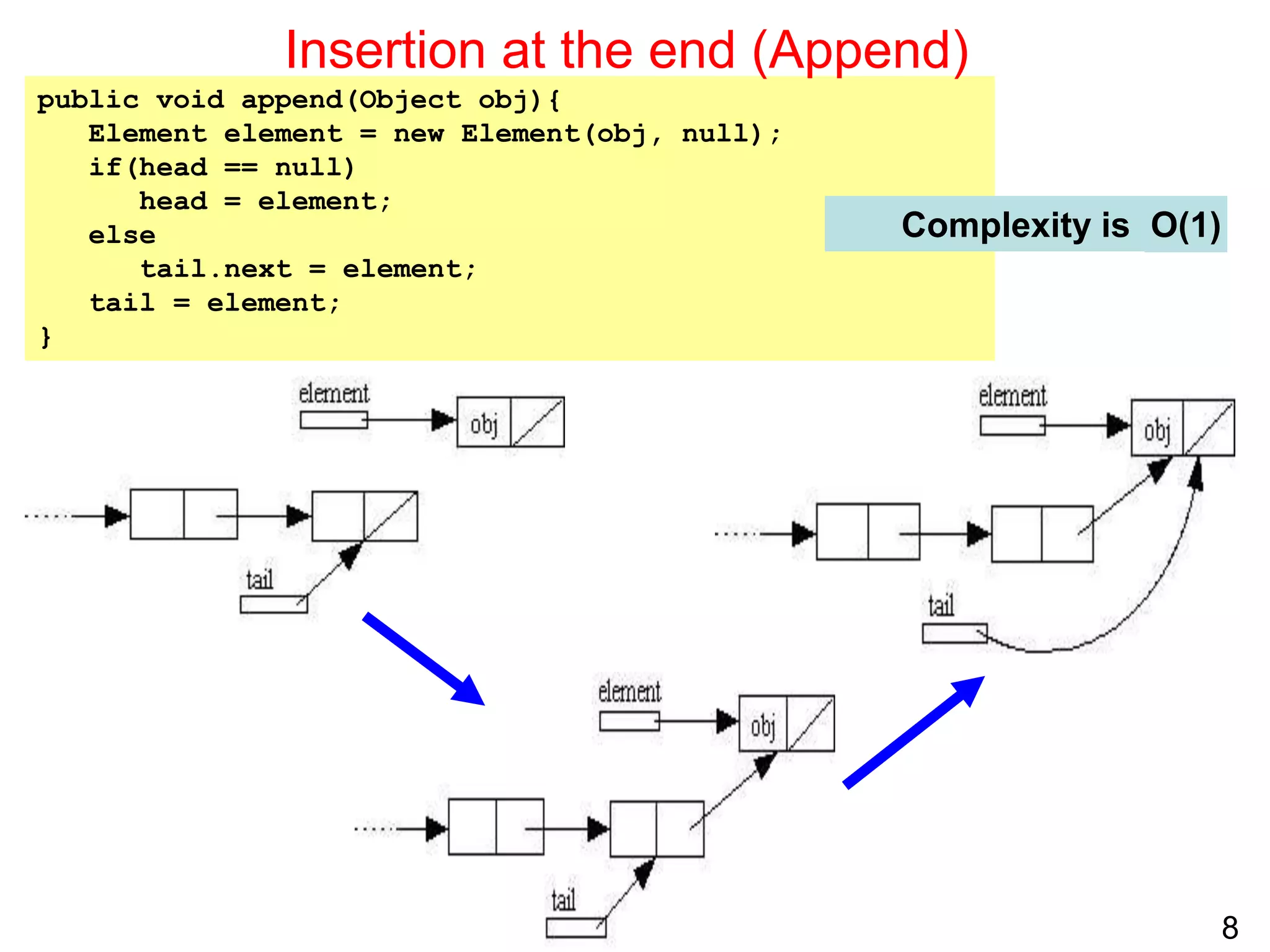
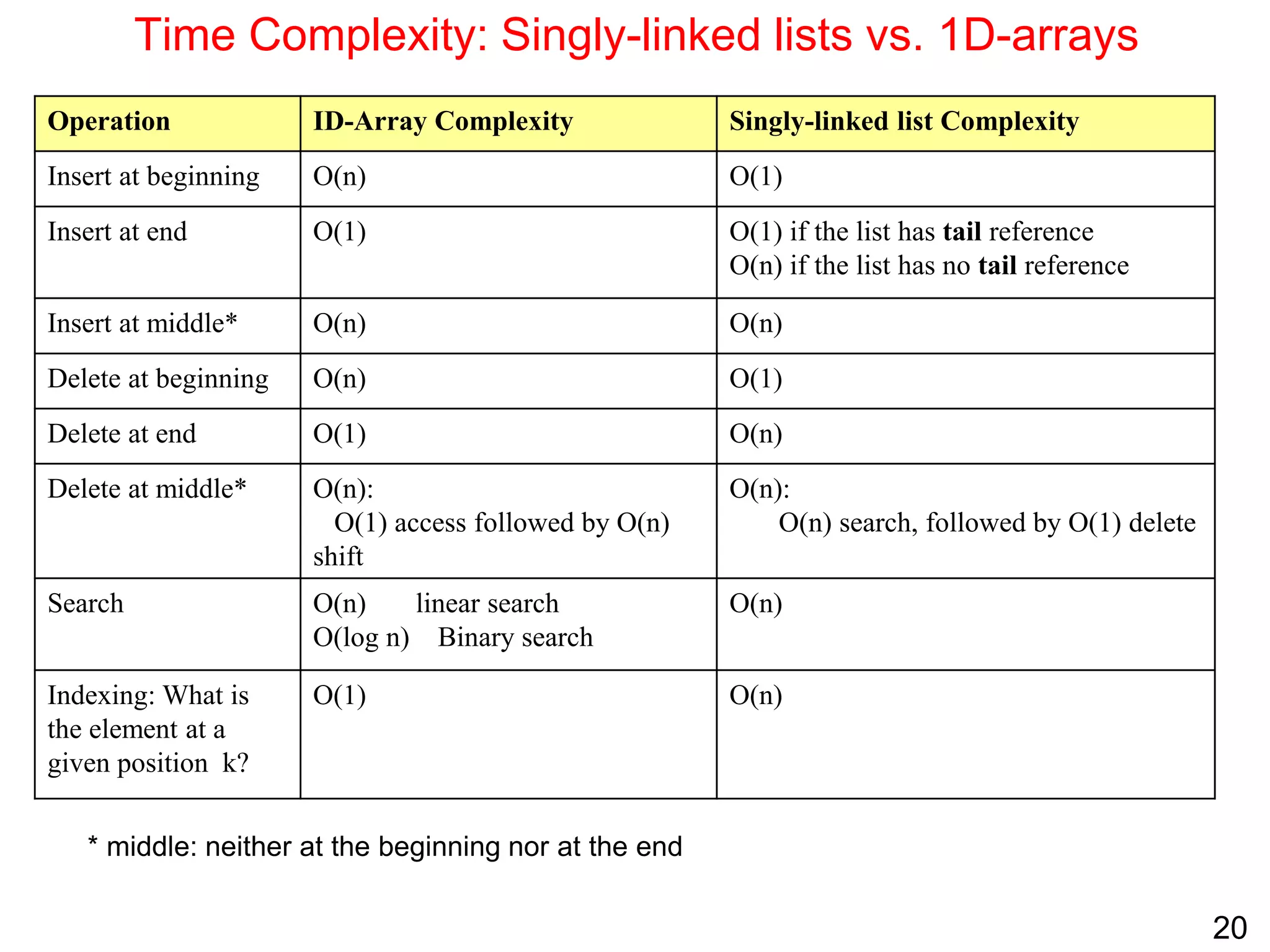
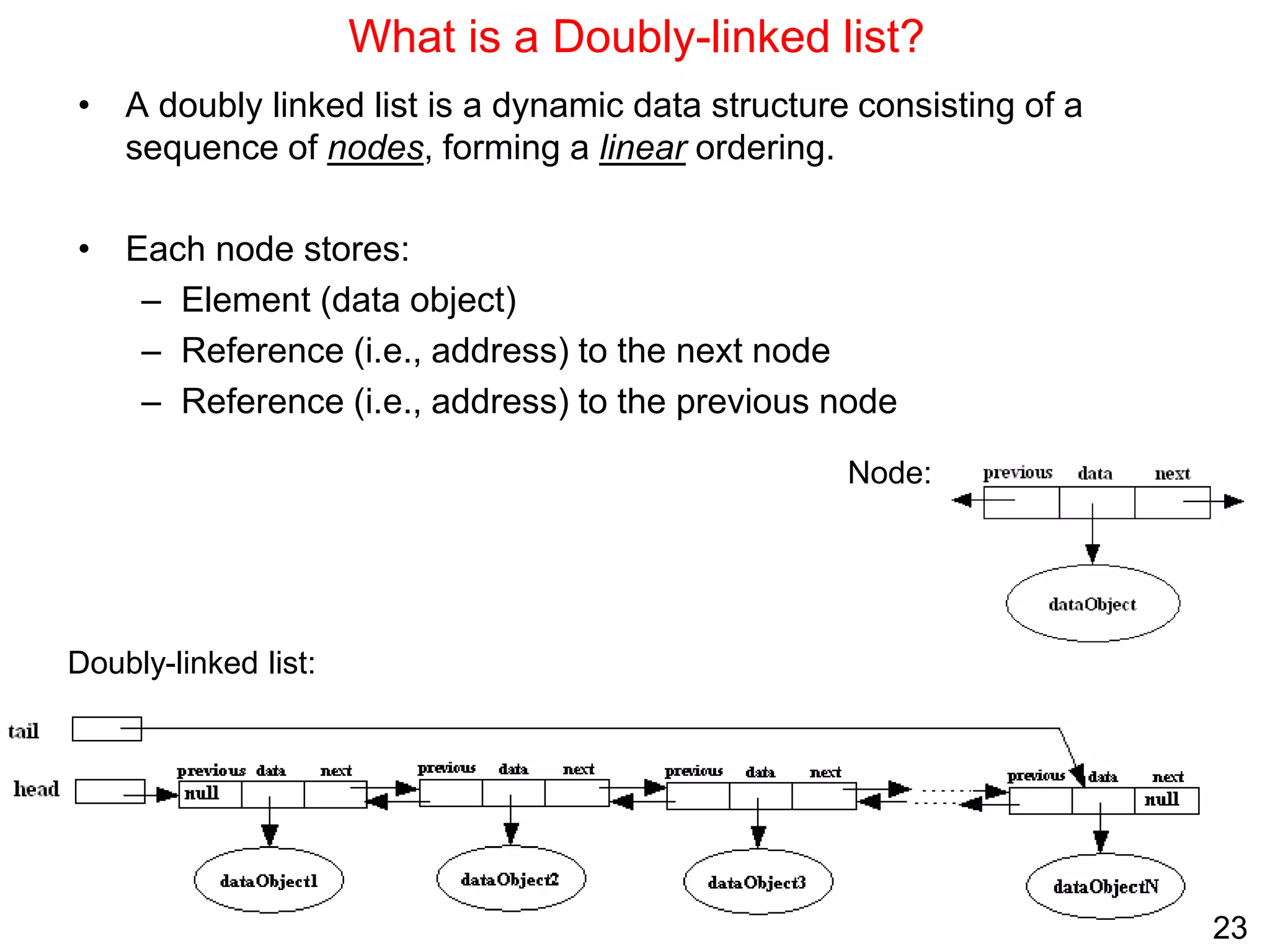
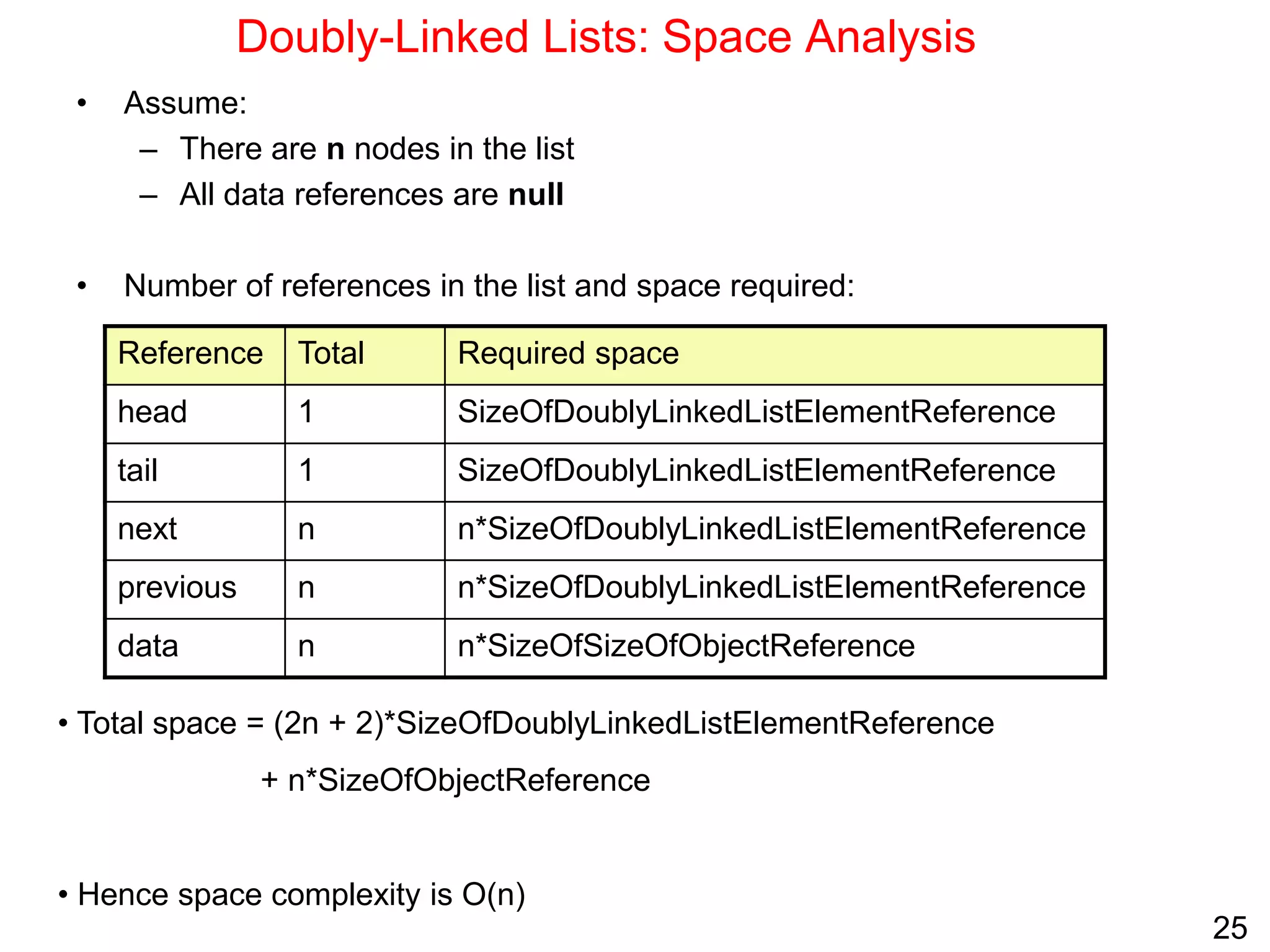
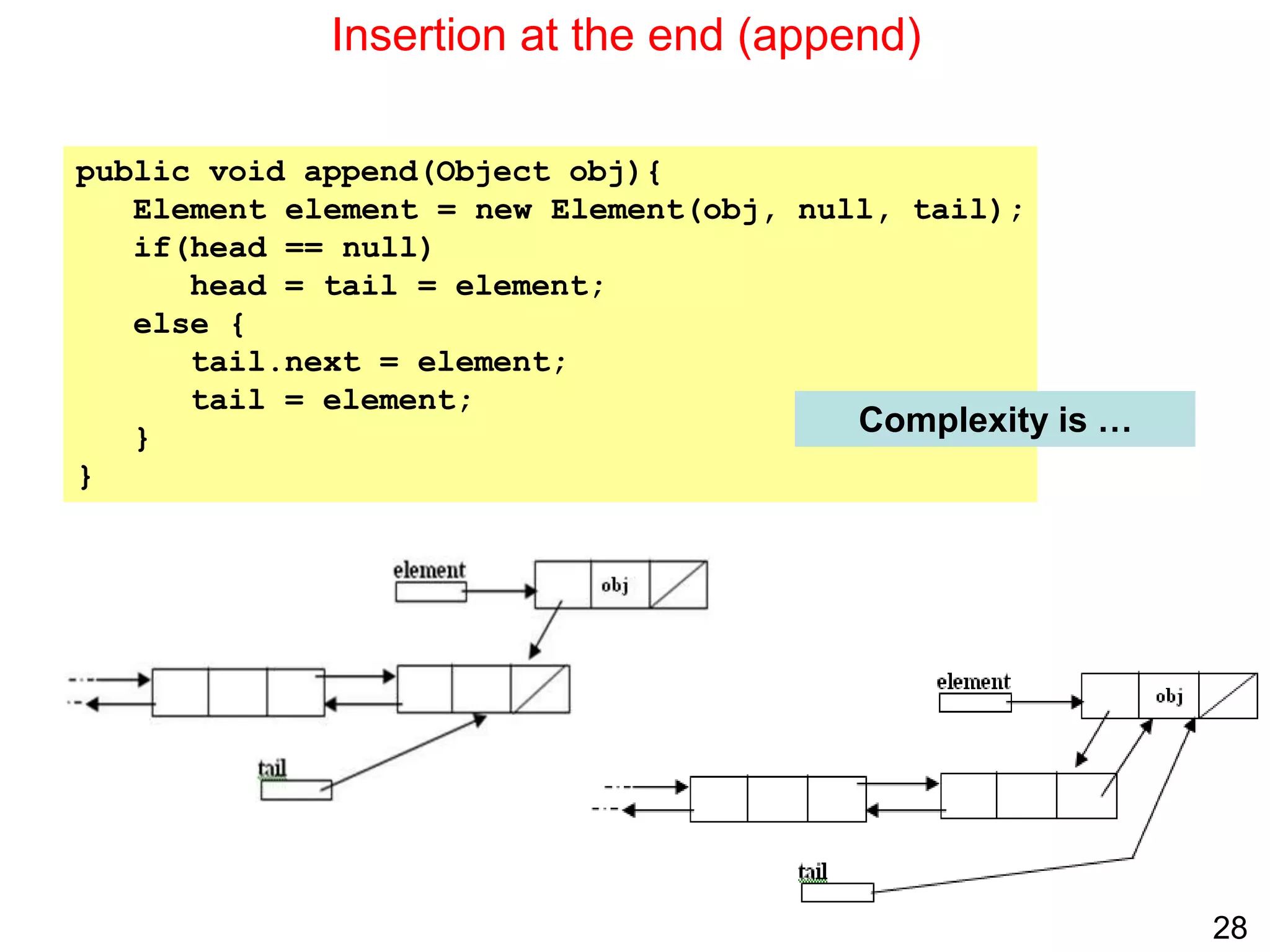
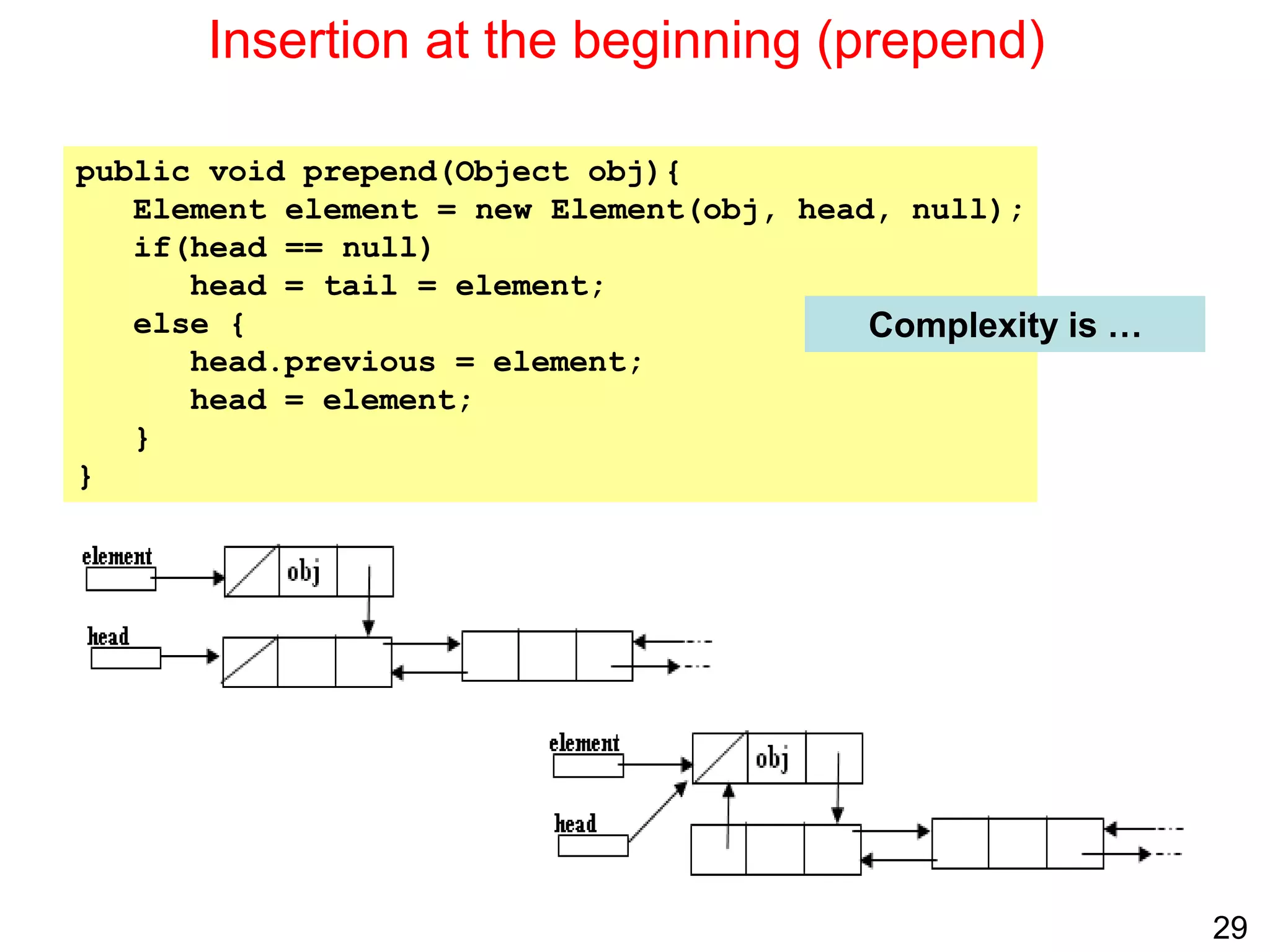
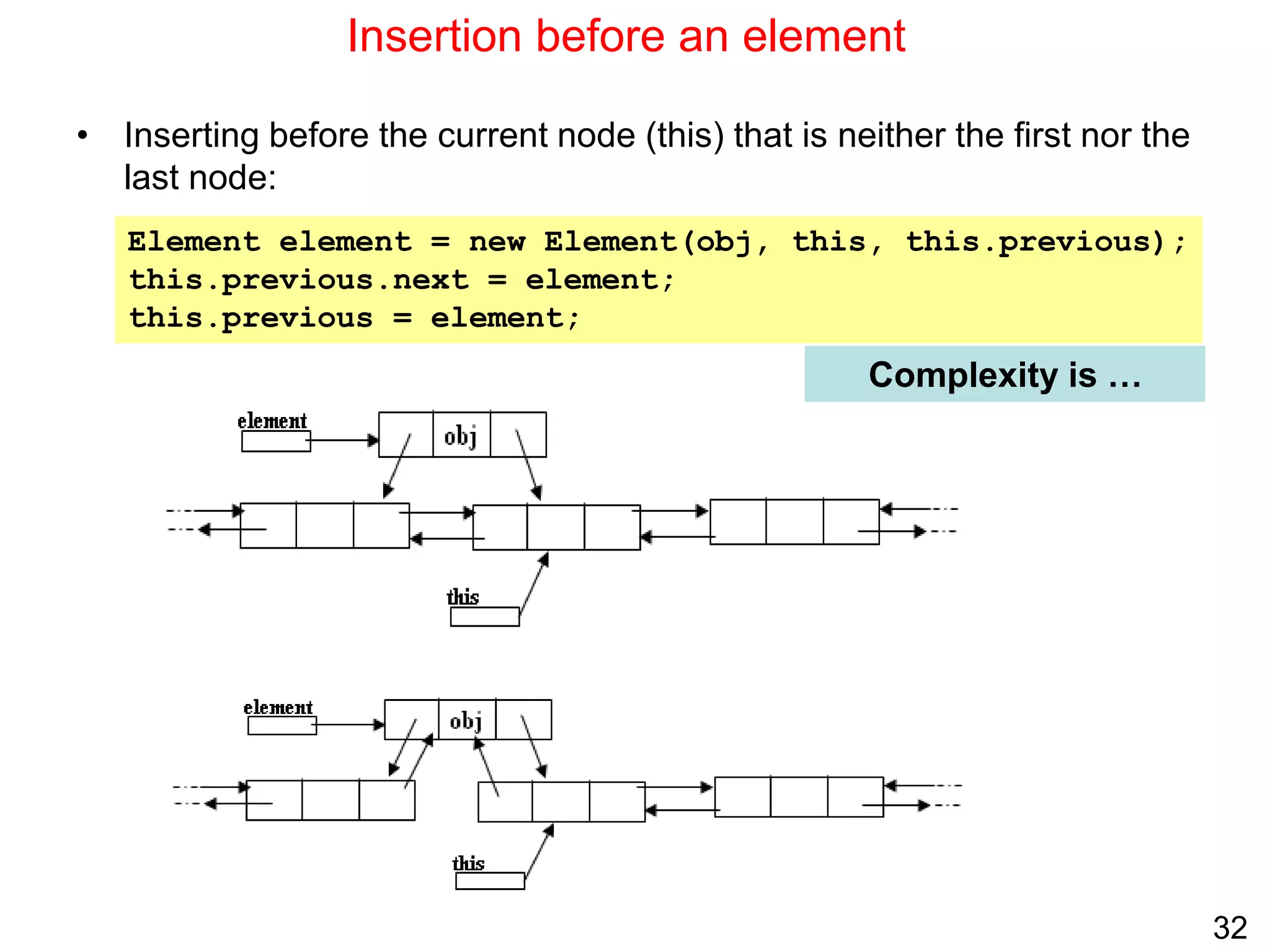
Singly linked lists allow for efficient insertion and deletion of elements without shifting other elements. They have dynamic size and use less memory than arrays if the list is sparsely populated. However, random access is not efficient as elements are not stored contiguously in memory. Common operations like search, insertion, and deletion have O(n) time complexity due to the need to traverse the list sequentially. Space complexity is O(n) to store the elements and references between nodes.

1. 1
Singly Linked Lists
• What is a singly-linked list?
• Why linked lists?
• Singly-linked lists vs. 1D-arrays
• Representation
• Space Analysis
• Creation, Append and Prepend
• Traversal
• Search
• Insertion after and before an element
• Deletion
• Time Complexity: Singly-linked lists vs. 1D-arrays

2. 2
What is a Singly-linked list?
• A singly linked list is a dynamic data structure consisting of a
sequence of nodes, forming a linear ordering.
• Each node stores:
– Element (data object)
– Reference (i.e., address) to the next node
Node:
Singly-linked list:

3. 3
Why linked lists?
• Linked lists are used to implement many important data structures
such as stacks, queues, graphs, hash tables, etc.
• Linked lists are used as components of some data structures.
Examples: B+ trees, skip lists, etc.
• LISP An important programming language in artificial intelligence
makes extensive use of linked lists in performing symbolic
processing.
• Memory management: An important role of operating systems. An
operating system must decide how to allocate and reclaim storage
for processes running on the system. A linked list can be used to
keep track of portions of memory that are available for allocation.
• Scrolled lists, components found in graphical user interfaces, can be
implemented using linked lists.

4. 4
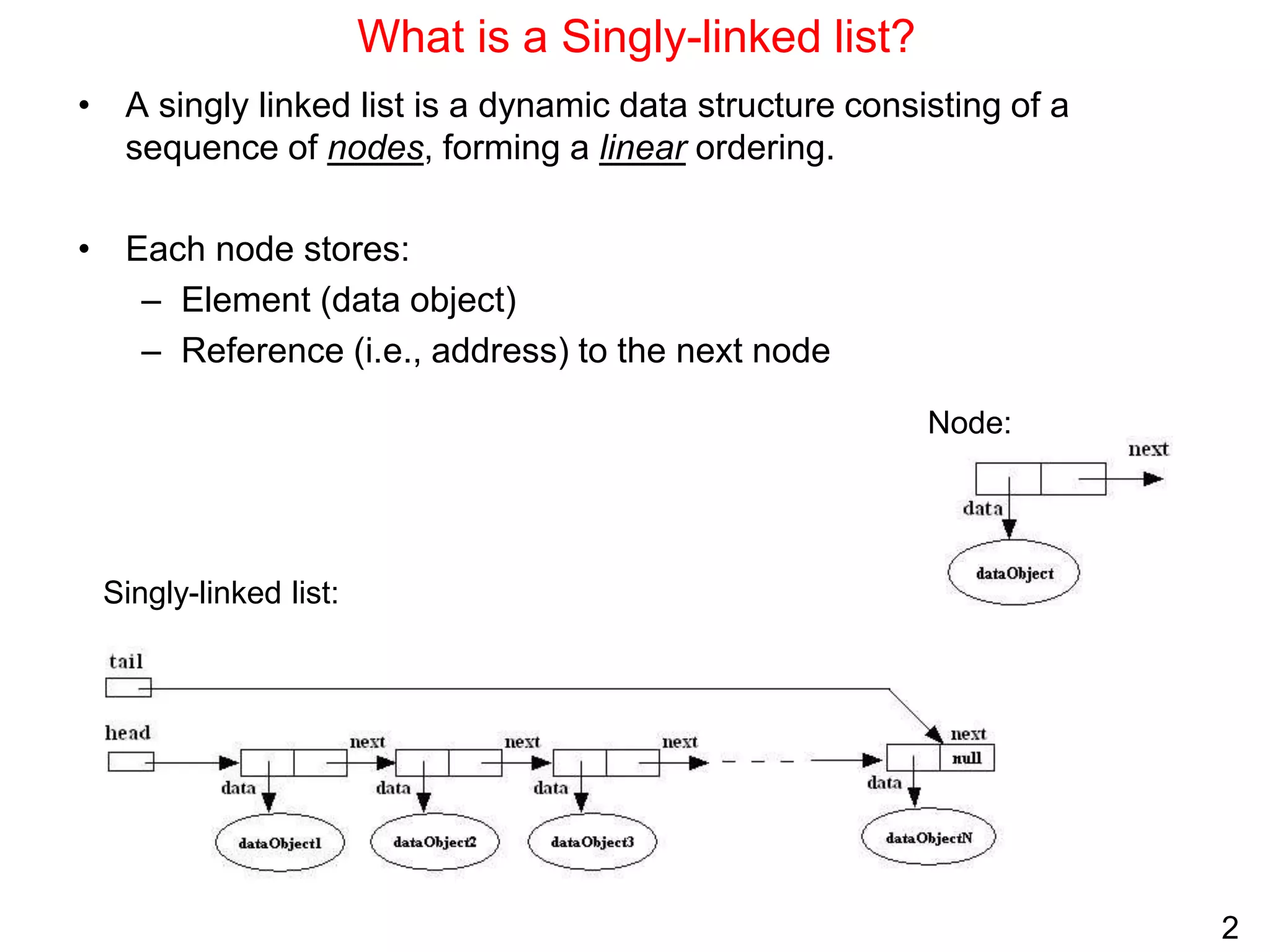
Singly-linked lists vs. 1D-arrays
ID-array Singly-linked list
Fixed size: Resizing is expensive Dynamic size
Insertions and Deletions are inefficient:
Elements are usually shifted
Insertions and Deletions are efficient: No
shifting
Random access i.e., efficient indexing No random access
 Not suitable for operations requiring
accessing elements by index such as sorting
No memory waste if the array is full or almost
full; otherwise may result in much memory
waste.
Extra storage needed for references; however
uses exactly as much memory as it needs
Sequential access is faster because of greater
locality of references [Reason: Elements in
contiguous memory locations]
Sequential access is slow because of low locality
of references [Reason: Elements not in
contiguous memory locations]

5. 5
Representation
• We are using a representation in which a linked list has both head
and tail references:
public class MyLinkedList{
protected Element head;
protected Element tail;
public final class Element{
Object data;
Element next;
Element(Object obj, Element element){
data = obj;
next = element;
}
public Object getData(){return data;}
public Element getNext(){return next;}
}
// . . .
}

6. 6
Representation: Space Analysis
• Assume:
– There are n nodes in the list
– All data references are null
• Number of references in the list and space required:
Required space
Total
Reference
SizeOfSinglyLinkedListElementReference
1
head
SizeOfSinglyLinkedListElementReference
1
tail
n*SizeOfSinglyLinkedListElementReference
n
next
n*SizeOfObjectReference
n
data
• Total space = (n + 2)*SizeOfSinglyLinkedListElementReference
+ n*SizeOfObjectReference
• Hence space complexity is O(n)

7. 7
List Creation
• An empty list is created as follows:
• Once created, elements can be inserted into the list using either the
append or prepend methods:
• Also if we have a reference to a node (an element), we can use the
insertAfter or InsertBefore methods of the Element class
MyLinkedList list = new MyLinkedList();
for (int k = 0; k < 10; k++)
list.append(new Integer(k));

8. 8
public void append(Object obj){
Element element = new Element(obj, null);
if(head == null)
head = element;
else
tail.next = element;
tail = element;
}
Insertion at the end (Append)
Complexity is O(1)

9. 9
public void prepend(Object obj) {
Element element = new Element(obj, head);
if(head == null)
tail = element;
head = element;
}
Insertion at the beginning (Prepend)
Complexity is O(1)

10. 10
Traversal
Begin at the first node, then follow each next reference until the
traversal condition is satisfied or until you come to the end.
To move an Element reference e from one node to the next use:
Example: Count the number of nodes in a linked list.
public int countNodes(){
int count = 0;
Element e = head;
while(e != null){
count++;
e = e.next;
}
return count;
}
e = e.next;
Complexity is O(n)

11. 11
Searching
• To search for an element, we traverse from head until we locate the object or
we reach the end of the list.
• Example: Count the number of nodes with data field equal to a given object.
public int countNodes(Object obj){
int count = 0;
Element e = head;
while(e != null){
if(e.data.equals(obj))
count++;
e = e.next;
}
return count;
}
Complexity is ….
• The following reference relationships are useful in searching:
e.next e.next.next e.next.next.next
e.next.data e.next.next.data
e
e.data
However, it is important to ensure that next is not null in such expressions

12. 12
Insertion after an element
• To insert an object y after a node x:
• Move a reference e from the beginning of the list to node x:
Element e = head;
if(e == null) throw new IllegalArgumentException(“not found”);
while(e != null && !e.data.equals(x)){
e = e.next;
}
if(e == null) throw new IllegalArgumentException(“not found”);
• Create a new node containing y as data and let its next reference refer to the
node after node x:
Element element = new Element(y, e.next);
• Make the next reference of node x refer to node y:
e.next = element;
• If the new node was inserted at the end of the list, update the tail reference:
if(element.next == null) tail = element;
e
e.next
x
e
e.next
x
y
element
e
e.next
x
y
element

13. 13
Insertion after an element
Complexity is
public void insertAfter(Object obj) {
// create a new node for obj2 and make it refer to the node
// after obj1 node
Element element = new Element(obj, this.next);
// make obj1 node refer to the new node
this.next = element;
// update tail if the new node was inserted at the end
if(this == tail)
tail = next;
}
Complexity is O(1)
O(n)
• The insertAfter method of the Element class is invoked as:
MyLinkedList.Element e = list.find(obj1);
if(e != null)
e.insertAfter(obj2); // insert obj2 after obj1
else
System.out.println("Element to insert before not found");
• Within the insertAfter method this refers to obj1 node:
• Note: The total complexity of the insert after operation is O(n) because find is O(n)

14. 14
Insertion before an element
• To insert an object y before a node x:
• Move a reference previous from the beginning of the list to the node before
node x:
Element e = head, previous;
if(e == null) throw new IllegalArgumentException(“not found”);
while(e != null && ! e.data.equals(x)){
previous = e;
e = e.next;
}
if(e == null) throw new IllegalArgumentException(“not found”);
• Create a new node containing y as data and let its next reference refer to the
node x:
Element element = new Element(y, e);
• Make the next reference of the node before node x refer to node y:
if(e == head)
head = element;
else
previous.next = element;
e
x
previous
y
element
e
x
previous
y
element
e
x
previous

15. 15
Insertion before an element
public void insertBefore(Object obj) {
// create a new node for obj2, make this node point to obj1 node
Element element = new Element(obj, this);
if(this == head){
head = element;
return;
}
Element previous = head;
// move previous to node before obj1 node
while(previous.next != this) {
previous = previous.next;
}
previous.next = element; // insert
}
Complexity is
MyLinkedList.Element e = list.find(obj1);
if(e != null)
e.insertBefore(obj2); // insert obj2 before obj1
else
System.out.println("Element to insert before not found");
• The insertBefore method of the Element class is invoked as:
• Within the insertBefore method this refers to obj1 node:
Complexity is O(n)
O(n)

16. 16
Deletion
• To delete a node x:
• Move a reference previous from the beginning of the list to the node before
node x:
Element e = head, previous;
if(e == null) throw new IllegalArgumentException(“not found”);
while(e != null && ! e.data.equals(x)){
previous = e;
e = e.next;
}
if(e == null) throw new IllegalArgumentException(“not found”);
• Bypass the node to be deleted:
if(e == head){
if(head.next == null)
head = tail = e = null;
else{
head = head.next;
}
else{
previous.next = e.next;
if(tail == e)
tail = previous;
}
e = null;
e
x
previous
e
x
previous

17. 17
Deletion – Deleting First and Last Element
public void extractFirst() {
if(head == null)
throw new IllegalArgumentException("item not found");
head = head.next;
if(head == null)
tail = null;
}
public void extractLast() {
if(tail == null)
throw new IllegalArgumentException("item not found");
if (head == tail)
head = tail = null;
else {
Element previous = head;
while(previous.next != tail)
previous = previous.next;
previous.next = null;
tail = previous;
}
}
Complexity is …
Complexity is …

18. 18
public void extract(Object obj) {
Element element = head;
Element previous = null;
while(element != null && ! element.data.equals(obj)) {
previous = element;
element = element.next;
}
if(element == null)
throw new IllegalArgumentException("item not found");
if(element == head)
head = element.next;
else
previous.next = element.next;
if(element == tail)
tail = previous;
}
Deletion of an arbitrary element
• To delete an element, we use either the extract method of MyLinkedList or
that of the Element inner class.
• The MyLinkedList extract method (code similar to that in slide 16):
Complexity is …
try{
list.extract(obj1);
} catch(IllegalArgumentException e){
System.out.println("Element not found");
}
• The method is invoked as:

19. 19
public void extract() {
Element element = null;
if(this == head)
head = next;
else{
element = head;
while(element != null && element.next != this){
element = element.next;
}
if(element == null)
throw new InvalidOperationException(“Not found”);
element.next = next;
}
if(this == tail)
tail = element;
}
Deletion of an arbitrary element
• The Element extract method invocation and implementation:
Complexity is …
MyLinkedList.Element e = list.find(obj1);
if(e != null)
e.extract();
else
System.out.println("Element not found");

20. 20
Time Complexity: Singly-linked lists vs. 1D-arrays
Operation ID-Array Complexity Singly-linked list Complexity
Insert at beginning O(n) O(1)
Insert at end O(1) O(1) if the list has tail reference
O(n) if the list has no tail reference
Insert at middle* O(n) O(n)
Delete at beginning O(n) O(1)
Delete at end O(1) O(n)
Delete at middle* O(n):
O(1) access followed by O(n)
shift
O(n):
O(n) search, followed by O(1) delete
Search O(n) linear search
O(log n) Binary search
O(n)
Indexing: What is
the element at a
given position k?
O(1) O(n)
* middle: neither at the beginning nor at the end

21. 21
Exercises
• Using the Element extract method is less efficient than using the
MyLinkedList extract method. Why?
• For the MyLinkedList class, Implement each of the following
methods:
– String toString()
– Element find(Object obj)
– void insertAt(int n) //counting the nodes from 1.
– void deleteBefore(Object obj) // delete node before obj node
State the complexity of each method.
• Which methods are affected if we do not use the tail reference in
MyLinkedList class.

22. 22
Doubly Linked Lists
• What is a doubly-linked list?
• Representation
• Space Analysis
• Doubly-linked lists vs. Singly-linked lists
• Creation, Append and Prepend
• Traversal
• Insertion before an element
• Deletion

23. 23
What is a Doubly-linked list?
• A doubly linked list is a dynamic data structure consisting of a
sequence of nodes, forming a linear ordering.
• Each node stores:
– Element (data object)
– Reference (i.e., address) to the next node
– Reference (i.e., address) to the previous node
Node:
Doubly-linked list:

24. 24
Representation
public class DoublyLinkedList{
protected Element head, tail;
//. . .
public class Element {
Object data;
Element next, previous;
Element(Object obj, Element next, Element previous){
data = obj; this.next = next;
this.previous = previous;
}
public Object getData(){return data;}
public Element getNext(){return next;}
public Element getPrevious(){return previous;}
// . . .
}
}

25. 25
Doubly-Linked Lists: Space Analysis
• Assume:
– There are n nodes in the list
– All data references are null
• Number of references in the list and space required:
Required space
Total
Reference
SizeOfDoublyLinkedListElementReference
1
head
SizeOfDoublyLinkedListElementReference
1
tail
n*SizeOfDoublyLinkedListElementReference
n
next
n*SizeOfDoublyLinkedListElementReference
n
previous
n*SizeOfSizeOfObjectReference
n
data
• Total space = (2n + 2)*SizeOfDoublyLinkedListElementReference
+ n*SizeOfObjectReference
• Hence space complexity is O(n)

26. 26
Doubly-Linked Lists vs. Singly-linked lists
• A doubly-linked list allows traversing the list in either direction.
• Modifying a doubly-linked list usually requires changing more references,
but is sometimes simpler because there is no need to keep track of the
address of the previous node. In singly-linked list, this is required in delete
and insert before operations.
 The extractLast operation is O(1) in doubly-linked list whereas it is
O(n) is singly-linked list
• Doubly-linked lists are used to implement dequeues (double-ended queues
that support insert or delete operations at either end).
• A singly-linked list uses less memory than an equivalent doubly-linked list.

27. 27
List Creation and Insertion
• An empty doubly-linked list is created as follows:
DoublyLinkedList list = new DoublyLinkedList();
• Like a singly-linked list, once created, elements can be inserted into
the list using either the append or prepend methods:
for (int k = 0; k < 10; k++)
list.append(new Int(k));
• Also if we have a reference to a node (an element), we can use the
insertAfter or InsertBefore methods of the Element class.

28. 28
Insertion at the end (append)
public void append(Object obj){
Element element = new Element(obj, null, tail);
if(head == null)
head = tail = element;
else {
tail.next = element;
tail = element;
}
}
Complexity is …

29. 29
Insertion at the beginning (prepend)
public void prepend(Object obj){
Element element = new Element(obj, head, null);
if(head == null)
head = tail = element;
else {
head.previous = element;
head = element;
}
}
Complexity is …

30. 30
Traversal
For DoublyLinked list, traversal can be done in either direction.
Forward, starting from the head, or backward starting from the tail.
Example: Count the number of nodes in a linked list.
Element e = head;
while (e != null) {
//do something
e = e.next;
}
Element e = tail;
while (e != null) {
//do something
e = e.previous;
}
public int countNodes(){
int count = 0;
Element e = head;
while(e != null){
count++;
e = e.next;
}
return count;
}
Complexity is …

31. 31
public int sumLastNnodes(int n){
if(n <= 0)
throw new IllegalArgumentException("Wrong: " + n);
if(head == null)
throw new ListEmptyException();
int count = 0, sum = 0;
Element e = tail;
while(e != null && count < n){
sum += (Integer)e.data;
count++;
e = e.previous;
}
if(count < n)
throw new IllegalArgumentException(“No. of nodes < "+n);
return sum;
}
Traversal (cont’d)
Example: The following computes the sum of the last n
nodes:
Complexity is …

32. 32
Insertion before an element
• Inserting before the current node (this) that is neither the first nor the
last node:
Complexity is …
Element element = new Element(obj, this, this.previous);
this.previous.next = element;
this.previous = element;

33. 33
Deletion
• To delete an element, we use either the extract method of
DoublyLinkedList or that of the Element inner class.
public void extract(Object obj){
Element element = head;
while((element != null) && (!element.data.equals(obj)))
element = element.next;
if(element == null)
throw new IllegalArgumentException("item not found");
if(element == head) {
head = element.next;
if(element.next != null)
element.next.previous = null;
}else{
element.previous.next = element.next;
if(element.next != null)
element.next.previous = element.previous;
}
if(element == tail)
tail = element.previous;
}
Complexity is …

34. 34
Exercises
• For the DoublyLinkedList class, Implement each of the following
methods and state its complexity.
– String toString()
– Element find(Object obj)
– void ExtractLast()
– void ExtractFirst()
– void ExtractLastN(int n)
• For the DoublyLinkedList.Element inner class, implement each of
the following methods and state its complexity.
– void insertBefore()
– void insertAfter()
– void extract()
• What are the methods of DoublyLinkedList and its Element inner
class that are more efficient than those of MyLinkedList class?