The Rabin Karp string matching algorithm has two versions that use hashing to determine if a pattern string exists within a text string. Version 1 assigns numeric weights to each character and sums the weights to generate a hash. Version 2 converts the string to a number in a given numeric base. Both versions calculate the hash of the pattern and slide it through the text, recomputing the hash at each position to check for a match. The complexity depends on the hash function used but can be O(n-m+1) in the best case where n and m are the string lengths.

1. Design and analysis of
algorithms
Prepared by: Aoun-Haider
FA21-BSE-133@cuilahore.edu.pk

2. Rabin Karp String Matching Algorithm:
• This algorithm has two basic versions.
• Take a hash function and generate a hash code and compare the code with
target string
• Complexity depends upon hash function we take
• Version#01: Take sum of weights assigned to each character and compare
sum with each possible pair of target string. If size of input string is ‘n’, pair
size will also be ‘n’ in the target string.
• Weights assigned can be user defined or based on ascii value of character
• Version#02: take a radix(base) and convert number into that base. For
example, if 26 alphabets are in the comparison then 26 will be base. If ascii
based comparison is taken, then 256 will be base.

3. Example: (Version#01)
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
a a a a a b
a a b
Input_str:
Hash_Function(a,a,b) = 1 + 1 +2 => 3
Character weights:
n = size of original string
m = size of input string
s = size of total characters in a table

4. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
a a a a a b
a a b
Input_str:
Hash_Function(a,a,b) = 1 + 1 +2 => 4
Hash_Function(a,a,a) = 1 + 1 +1 => 3
3 <> 4 -> move next

5. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
a a a a a b
a a b
Input_str:
Hash_Function(a,a,b) = 1 + 1 +2 => 4
Hash_Function(a,a,a) = 1 + 1 +1 => 3
3 <> 4 -> move next

6. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
a a a a a b
a a b
Input_str:
Hash_Function(a,a,b) = 1 + 1 +2 => 4
Hash_Function(a,a,a) = 1 + 1 +1 => 3
3 <> 4 -> move next

7. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
a a a a a b
a a b
Input_str:
Hash_Function(a,a,b) = 1 + 1 +2 => 4
Hash_Function(a,a,a) = 1 + 1 +2 => 4
4 == 4 -> compare both strings
So, String exist.
O( n – m +1)

8. Worst Case:
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7

9. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 3 + 3 +1 => 7
7 == 7 -> compare both strings
Not Equal -> move next

10. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 3 + 1 +3 => 7
7 == 7 -> compare both strings
Not Equal -> move next

11. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 1 + 3 +3 => 7
7 == 7 -> compare both strings
Not Equal -> move next

12. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 3 + 3 +1 => 7
7 == 7 -> compare both strings
Not Equal -> move next

13. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 3 + 1 +1 => 5
5 <> 7 -> move next

14. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 1 + 1 +5 => 7
7 == 7 -> compare both strings
Not Equal -> move next

15. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 1 + 5 +4 => 10
10 <> 7 -> move next

16. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 5 + 4 +2 => 11
11 <> 7 -> move next

17. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
Input_str: b d a
Hash_Function(b,d,a) = 2 + 4 +1 => 7
Hash_Function(a,a,a) = 4 + 2 +1 => 7
7 == 7 -> compare both strings
Not Equal -> String not found!!
≈ O(nm)

18. Version#02:
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
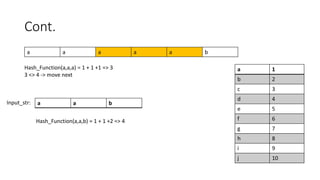
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(c1,c2,…,cn) = P[0] x sm-1 + P[1] x sm-2 + P[2] x sm-3
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
m = 3
s = 10

19. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(c,c,a) = 3 x 102 + 3 x 101 +1 x 100=> 331
331 <> 421 -> move next

20. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
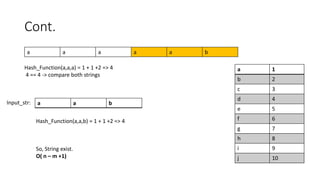
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(c,a,a) = 3 x 102 + 1 x 101 +3 x 100=> 313
OR [[3 x 102 + 3 x 101 +1 x 100] – 3 x 102 ] x 3 x 100
[[3 x 102 + 3 x 101 +1 x 100] – 3 x 102 ] x 3
313 <> 421 -> move next

21. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(a,c,c) = 1 x 102 + 3 x 101 +3 x 100=> 133
OR [[3 x 102 + 1 x 101 +3 x 100] – 3 x 102 ] x 3 x 100
[[3 x 102 + 1 x 101 +3 x 100] – 3 x 102 ] x 3
133 <> 421 -> move next

22. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
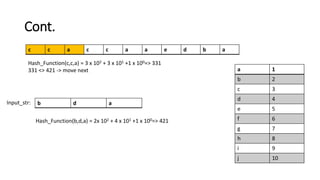
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(c,c,a) = 3 x 102 + 3 x 101 +1 x 100=> 331
OR [[1 x 102 + 3 x 101 +3 x 100] – 3 x 102 ] x 1 x 100
[[1 x 102 + 3 x 101 +3 x 100] – 3 x 102 ] x 1
331 <> 421 -> move next

23. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(c,a,a) = 3 x 102 + 1 x 101 +1 x 100=> 331
OR [[3 x 102 + 3 x 101 +1 x 100] – 3 x 102 ] x 1 x 100
[[3 x 102 + 3 x 101 +1 x 100] – 3 x 102 ] x 1
331 <> 421 -> move next

24. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(a,a,e) = 1 x 102 + 1 x 101 +5 x 100=> 115
OR [[3 x 102 + 1 x 101 +1 x 100] – 3 x 102 ] x 5 x 100
[[3 x 102 + 1 x 101 +1 x 100] – 3 x 102 ] x 5
115 <> 421 -> move next

25. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(a,a,e) = 1 x 102 + 5 x 101 +4 x 100=> 154
OR [[1 x 102 + 1 x 101 +5 x 100] – 3 x 102 ] x 4 x 100
[[1 x 102 + 1 x 101 +5 x 100] – 3 x 102 ] x 4
154 <> 421 -> move next

26. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(a,a,e) = 5 x 102 + 4 x 101 +2 x 100=> 542
OR [[1 x 102 + 5 x 101 +4 x 100] – 1 x 102 ] x 2 x 100
[[1 x 102 + 5 x 101 +4 x 100] – 1 x 102 ] x 2
542 <> 421 -> move next

27. Cont.
a 1
b 2
c 3
d 4
e 5
f 6
g 7
h 8
i 9
j 10
c c a c c a a e d b a
b d a
Input_str:
Hash_Function(b,d,a) = 2x 102 + 4 x 101 +1 x 100=> 421
Hash_Function(a,a,e) = 4 x 102 + 2 x 101 +1 x 100=> 421
OR [[5 x 102 + 4 x 101 +2 x 100] – 1 x 102 ] x 1 x 100
[[5 x 102 + 4 x 101 +2 x 100] – 1 x 102 ] x 1
421 == 421 -> Compare string -> String not found!!
O(n-m+1)

28. Comments:
• Complexity of rabin karp algorithm depends upon hash function we
choose.
• First version has problem of getting same sum multiple time and
requires a lot of comparisons which takes O(nm)
• The 2nd version still arise a problem. If a 32-bit integer is whose
system limit and number generate is large enough or exceed from 32
bits can cause spurious hits.
• Solution: We can also take mod of the hash function to get little
number with 231 because range is 0-31.