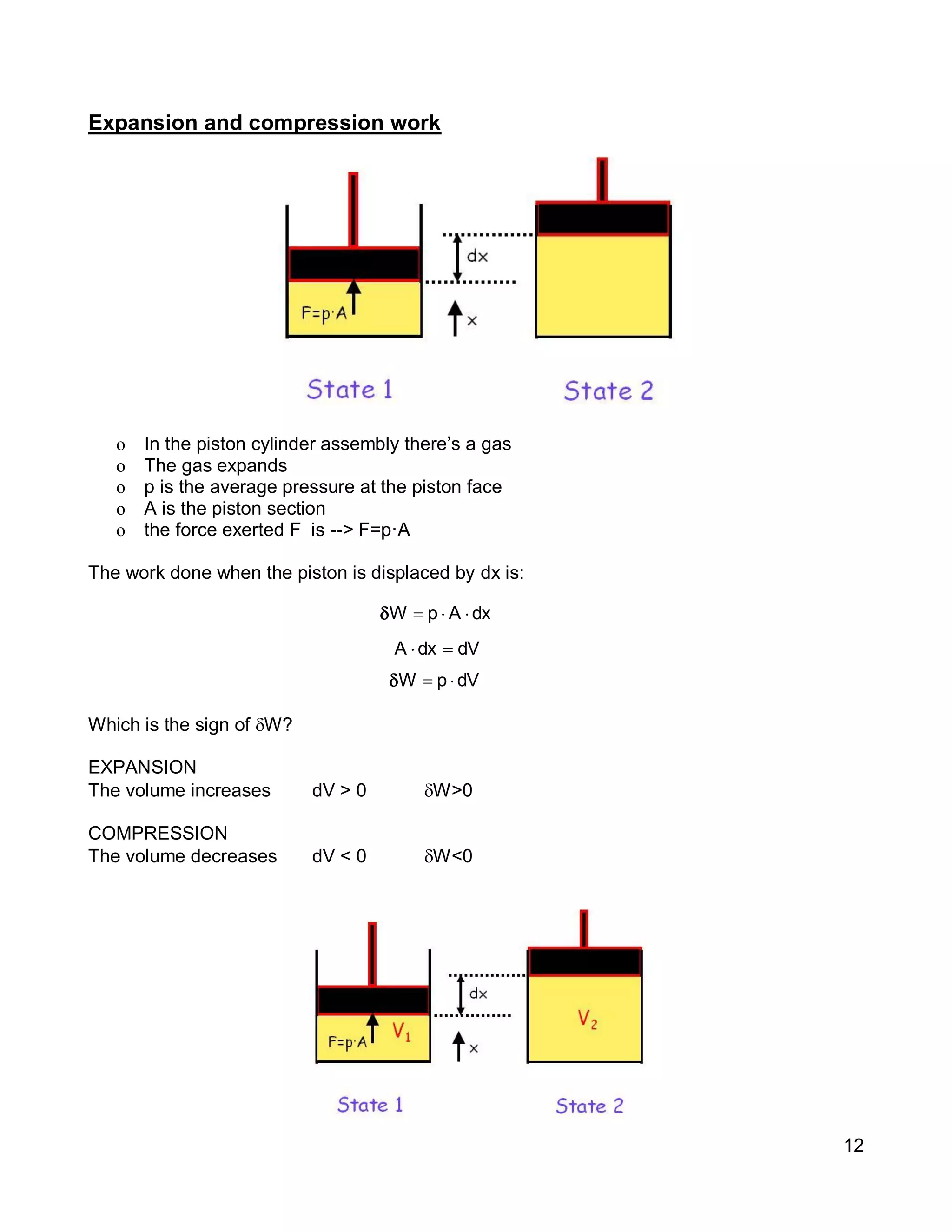
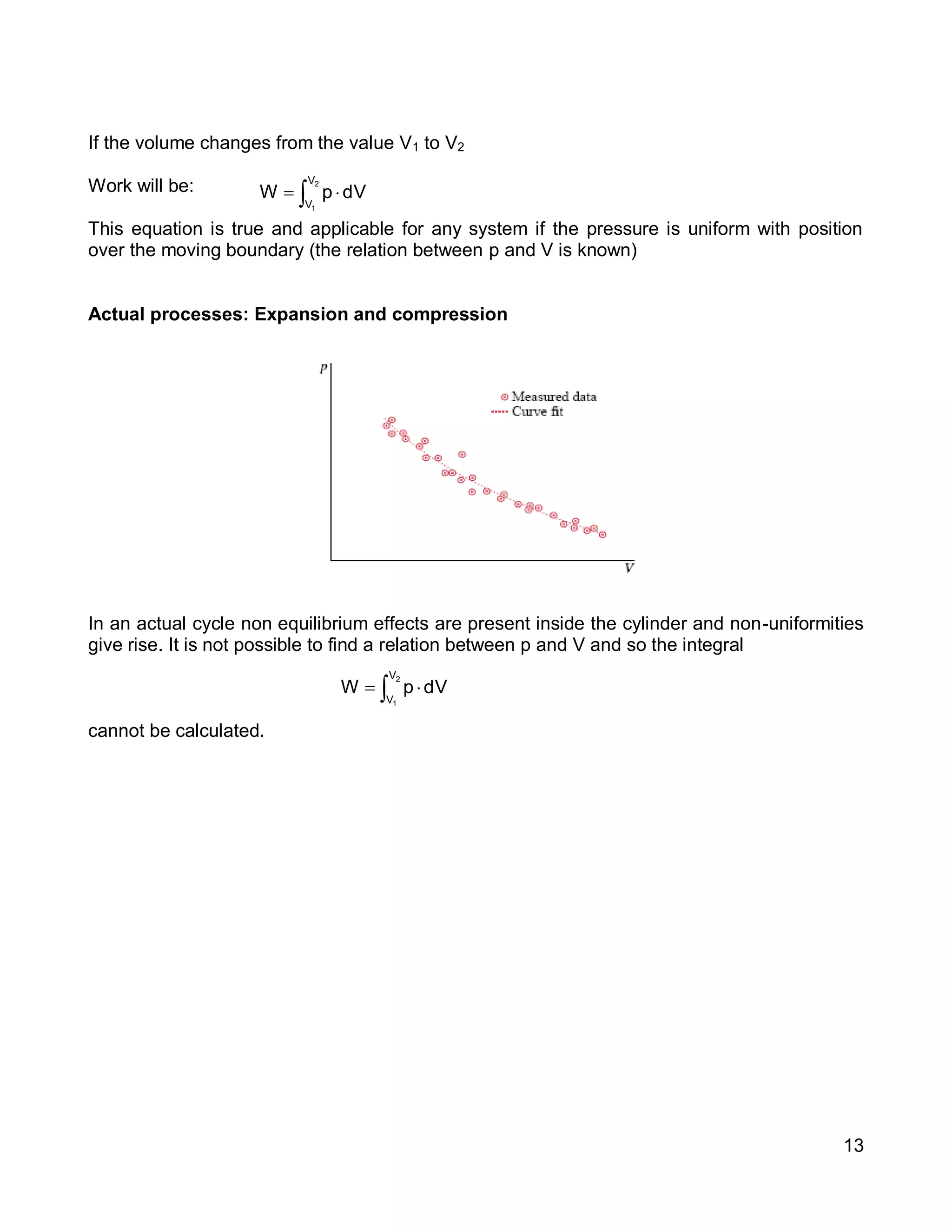
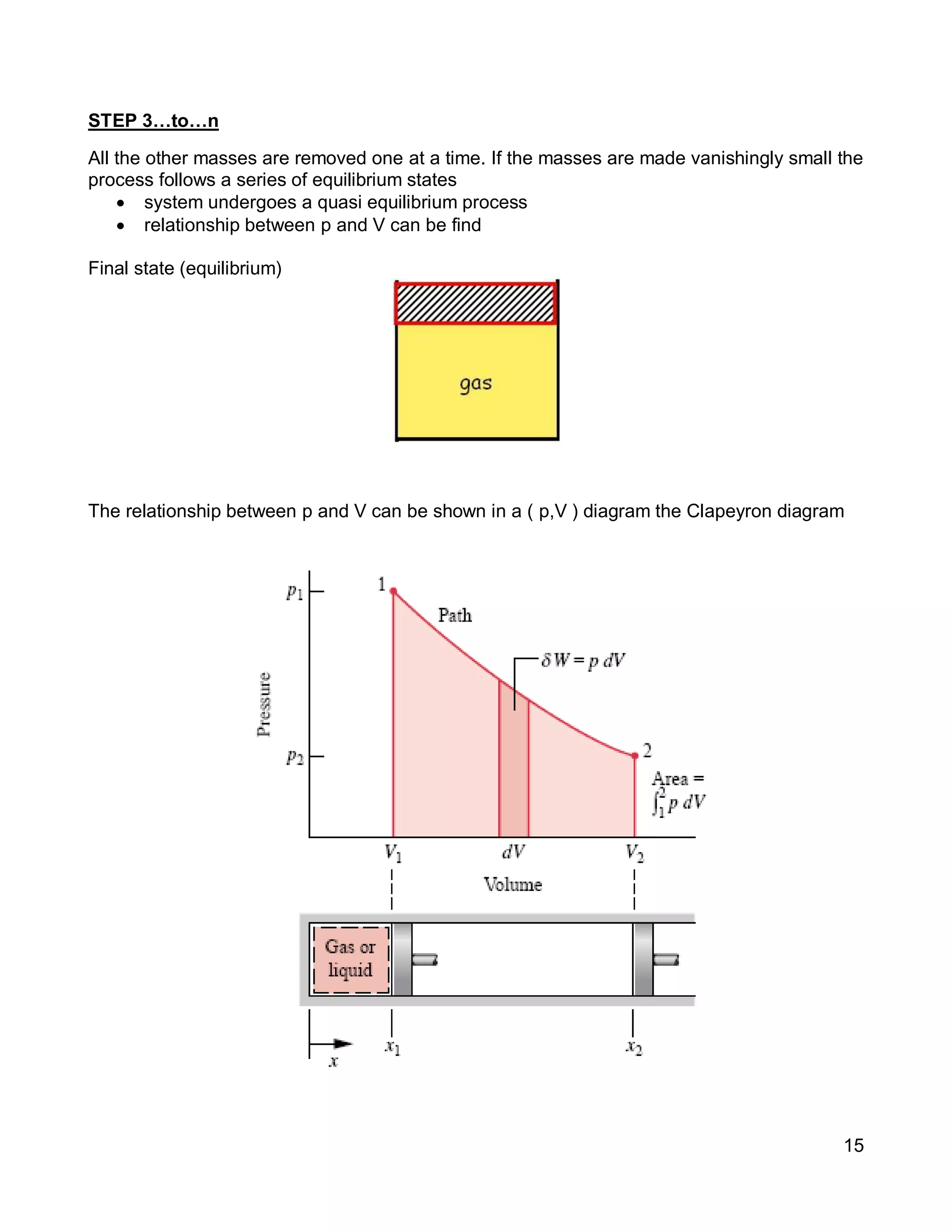
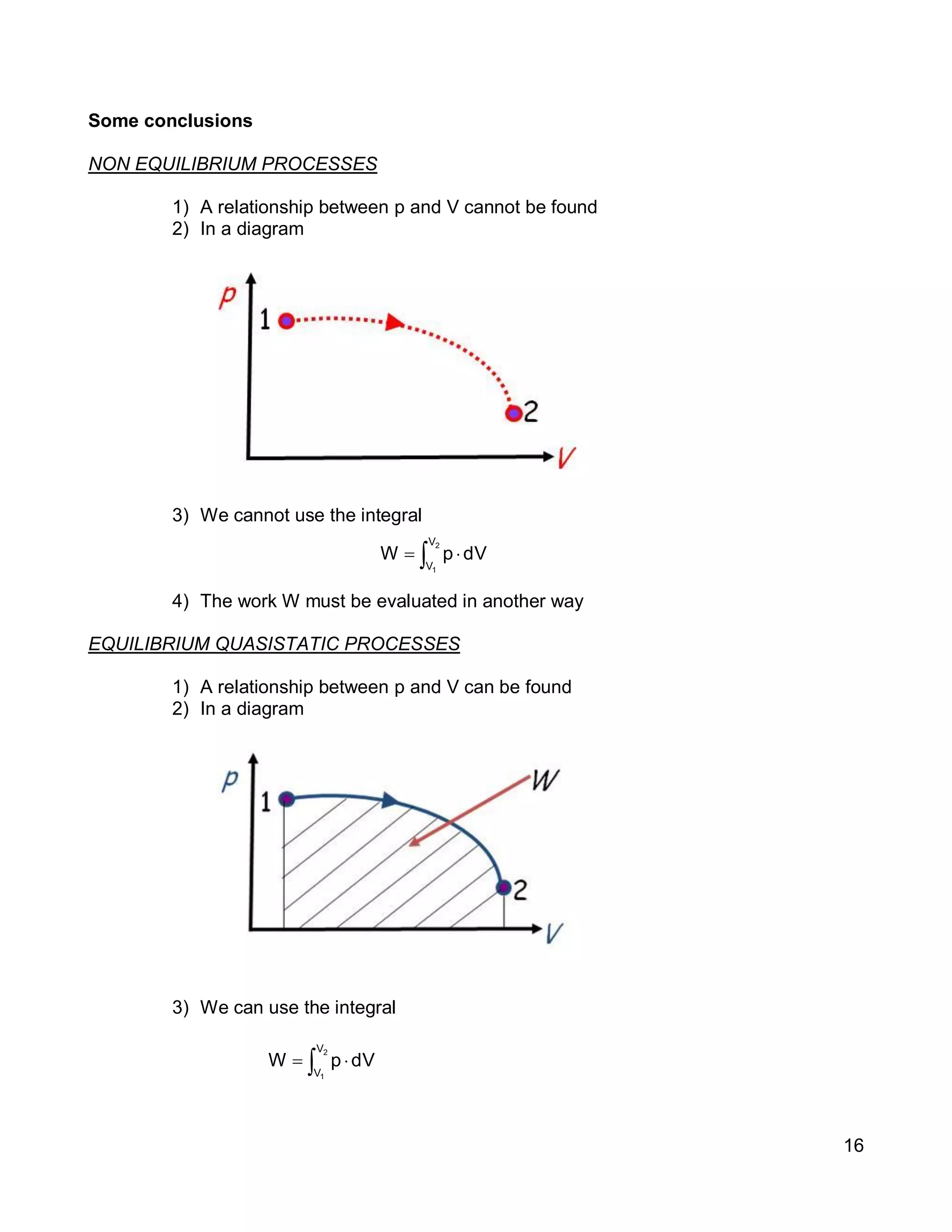
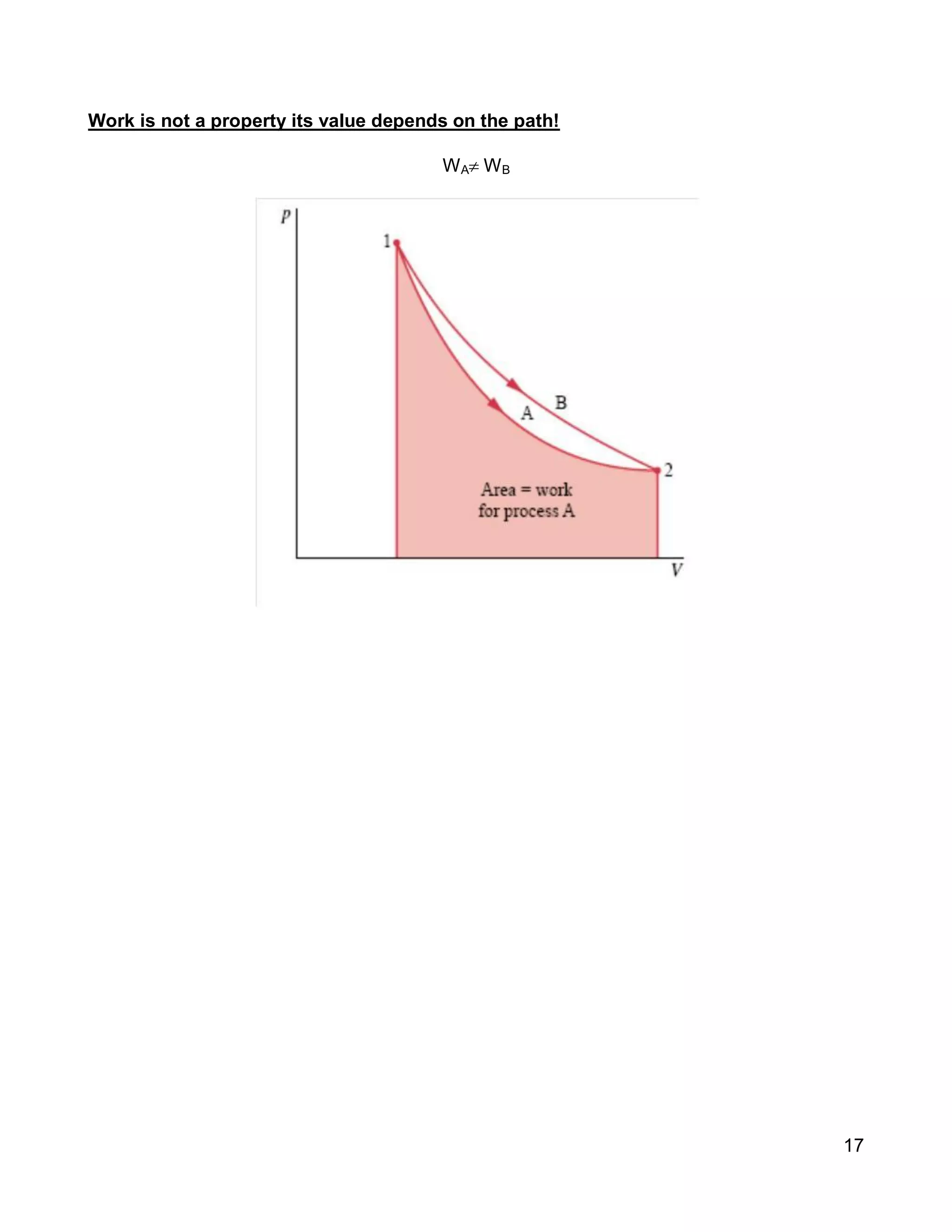
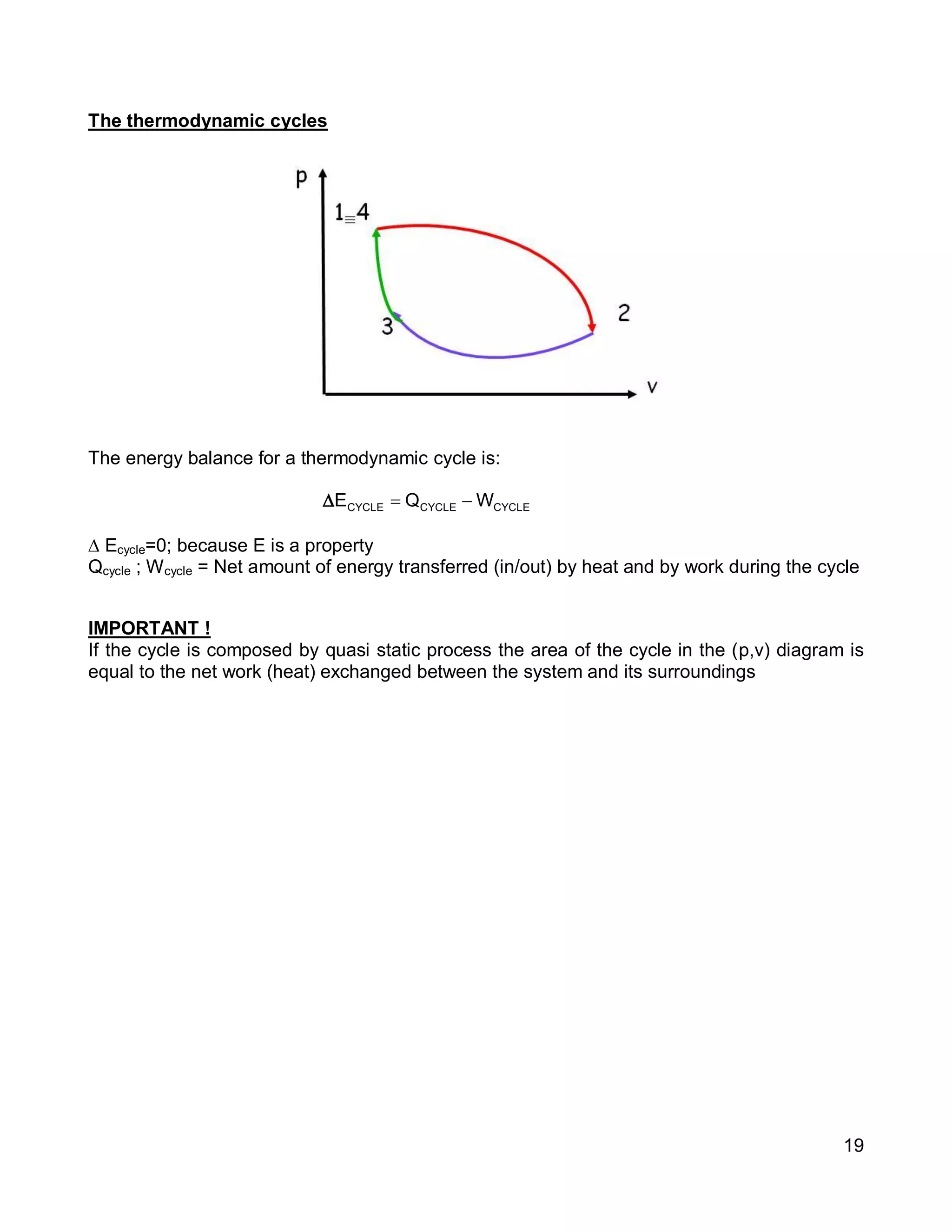
1. The document provides an introduction to thermal systems and the first law of thermodynamics for closed systems. 2. It defines key concepts such as systems, surroundings, properties, state, equilibrium, steady state, processes, cycles, and forms of energy including heat and work. 3. Thermal systems can be closed, open, or isolated and undergo processes that may or may not be quasi-equilibrium. The first law relates changes in internal energy of closed systems to heat and work.

1. 1
1 Lecture notes
CONTENTS
 Introduction to thermal systems:
 System description
 Energy
 1st Law of Thermodynamics closed systems

2. 2
Introduction to Thermodynamics
Thermodynamics is the science of energy and energy can be viewed as the ability to cause
changes.
Classical thermodynamics: macroscopic approach, the matter is a continuum, hypothesis of
spatial homogeneity
Statistical thermodynamics: microscopic approach
Thermal systems: definitions
SYSTEM: is whatever we want to study
A system is a quantity of matter or a region in space we have chosen to study
o May be simple (free body) or complex (e.g. power plant)
o The quantity of matter contained within the system may be fixed or not
The mass or region outside the system is the SURROUNDINGS
The real o ideal surface separating the system from its surroundings is called BOUNDARY
Boundary: the contact surface shared by both the system and the surroundings (math. p. of
v. it has zero thickness and so no mass & volume)
The interaction between the system and its surroundings takes place across the boundary
The boundary may be fixed or movable

3. 3
Different kinds of systems
o Closed systems
o Open systems (Control volume)
o Insulated system
CLOSED SYSTEM: a system is closed when there is no mass transfer across its boundary. A
closed system always contains the same quantity of matter.
OPEN SYSTEM (CONTROL VOLUME): is a system for which a mass flow rate can cross the
boundary.
To study this kind of systems we must refer to a given region of space (“control volume”)
through which mass flows and to a control surface.
ISOLATED SYSTEM: is a special type of closed system that does not interact in any way with
its surroundings

4. 4
SYSTEMS DESCRIPTION:
PROPERTIES
In order to describe the system and its behavior we must know:
-the system properties and
-how these properties are related
PROPERTY: is a macroscopic feature of the system (e.g. mass m, volume V, pressure p,
temperature T, etc.)
The properties may be:
 EXTENSIVE properties are those properties that have a numerical value that is
proportional to the system size (they are additive): mass (M), volume (V), internal
energy (U),
 INTENSIVE properties are those properties that have a numerical value that is
independent of the mass of the system (they are not additive): pressure (p),
temperature (T), etc..
Extensive properties per unit mass are called specific properties (v=V/m specific volume)
A property is known when we can assign a numerical value to that property at a given time
(no knowledge of the previous behavior!)
STATE: is the condition in which the system is as described by its properties
At a given state all the properties of the system have a fixed value.
If the value of even one property changes the state of the system will change.

5. 5
EQUILIBRIUM
The mechanics point of view: a system is in equilibrium if there is a condition of balance due
to equality of opposing forces
Example:
The thermodynamics point of view: the equilibrium condition (state) is reached when our
system reaches, at the same time, the mechanical, thermal, chemical and phase equilibrium.
In order to have a system in thermodynamic equilibrium it’s necessary that all the relevant
equilibrium criteria are satisfied:
 Thermal equilibrium: the temperature is the same throughout the whole system
 Mechanical equilibrium: the pressure is the same at any point of the system
 Phase equilibrium:
PURE SUBSTANCE: is one that is uniform/homogeneous and invariable in chemical
composition
PHASE: is the term used to define a quantity of matter that is homogenous both in
chemical composition and in physical structure (solid, liquid, vapor)
Example: Liquid water+ water vapor
Pure substance
Two phases
 Chemical equilibrium: the chemical composition doesn’t change with time (no
reaction occurs)
In order to fix the state it is not necessary to specify the value of all the properties cause:
• Among the system’s properties usually there are relations
• A subset of properties is sufficient to describe the system
• The other properties can be determined in terms of these few (the subset)

6. 6
STEADY STATE: a system is at steady state if none of its properties changes with time
PROCESS: is a transformation during which the system changes its state and so its
properties
PATH: is the series of state (equilibrium) through which a system passes during a process
If a system has all the same properties at two different times it results in the same state at
these times
THERMODYNAMIC CYCLE: is the sequence of a series of processes that begins and ends
at the same state
IMPORTANT!
 After the end of the cycle all the properties have the same value that they had at the
beginning
NO NET CHANGE OF STATE OCCURS!
 Properties are independent of the details of the process
QUASI EQUILIBRIUM PROCESS
When a process proceeds in such a manner that the system remains infinitesimally close to
an equilibrium state at all times, it’s called QUASI STATIC or QUASI EQUILIBRIUM
PROCESS. It’s a:
 idealized process
 departure from the equilibrium state is at most infinitesimal

7. 7
 the whole system can be describe by using only a numerical value for each property
Actual process & the equilibrium state
 equilibrium state condition is satisfied only at the beginning and at the end of the
process
 spatial variation in intensive properties at a given time is present
 for each property only a numerical value is not sufficient

8. 8
FORMS OF ENERGY:
Thermal systems involve energy:
 Storage
 Transfer
 Conversion
STORAGE: (within the matter that constitutes the system): kinetic energy, gravitational
potential energy, etc.
TRANSFER: (between system and its surroundings): work, heat transfer, flow of streams of
matter
CONVERSION: (from a form to another): e.g. energy associated to combustion process
Energy exists in different for such as: thermal, mechanical, kinetic, potential, magnetic,
chemical, nuclear, etc. Their sum constitutes the total energy E of the system (J) on a unit
mass basis e (J/kg)
We are not interested in the absolute value of the total energy (E=0 in an assigned reference
point) but we’re interested in its change.
In thermodynamic we’ll subdivide the forms of energy that make up the total energy in two
groups:
 Macroscopic forms: the ones the system has in respect to an outside reference frame
(surroundings)
 Microscopic forms: the ones related to the molecular activity and they’re independent
of any outside reference
KINETIC ENERGY
Body of mass m moving from point 1(𝑣̅1) to point 2 (𝑣̅2)
The change in kinetic energy (KE) is :
∆(KE)=(KE)2-(KE)1=
1
2
m (𝑣̅2
2
-𝑣̅1
2
) [Joule, J]
KE is a property of the body and it’s an extensive property; on an unit mass basis ke (J/kg)
POTENTIAL ENERGY
Body of mass m, moving from point 1(z1) to point 2(z2), in a field with a specified gravity
acceleration (g) value.
The change in potential energy (PE) is:
∆(PE)=(PE)2-(PE)1=m g ( 𝑧2-𝑧1) [Joule, J]
PE is a property of the body and it’s an extensive property; on an unit mass basis pe (J/kg)

9. 9
INTERNAL ENERGY
Internal energy lumps together all the other microscopic forms of energy
INTERNAL ENERGY: -symbol U
-SI units (Joule)
-U is an extensive property
TOTAL ENERGY
𝐸 = 𝐾𝐸 + 𝑃𝐸 + 𝑈 = 𝑚
𝑣̅2
2
+ 𝑚𝑔𝑧 + 𝑈
𝑒 = 𝑘𝑒 + 𝑝𝑒 + 𝑢 =
𝑣̅2
2
+ 𝑔𝑧 + 𝑢
The change E in the total energy of a system is:
Most closed systems remain stationary during a process and so experience no changes in
kinetic and potential energy.
Ex. closed system whose velocity and elevation of the center of gravity remains constant
during a process
     12121212 UUPEPEKEKEEEE 
 1212 UUUEEE  

10. 10
HEAT (Energy transfer by heat)
Closed systems can interact with their surroundings and energy can cross their boundaries
(heat and work)
HEAT: by definition is the form of energy that is transferred between two systems (or a
system and its surroundings) due to a difference in temperature.
Hence there cannot be any heat transfer between two systems that are at the same
temperature.
The symbol commonly used is Q and the units are Joule.
The heat transferred per unit mass is q (J/kg)
The rate of heat transfer, which is the heat transferred per unit time is Q̇ (W).
If Q̇ varies with time
Sign convention
Q>0 when heat is transferred TO the system
Q<0 when heat is removed FROM the system
Heat is a quantity transferred between systems or between a system and its surroundings
and for this reason it is not a PROPERTY cause the amount of heat depends more than just
the state of the system.
Heat is an energy transfer mechanism between a system and its surroundings
 Heat transfer takes place at the system boundary, and so it’s a BOUNDARY
PHENOMENON
 The system has a certain energy level but doesn’t have a certain heat
 It’s associated with a process not with a state
 Heat is a PATH FUNCTION and so its magnitude will depend on the path followed
during the process as well as the initial and the final states
Path functions have an inexact differential while point(state) functions (the properties that
depend on the state only) have an exact differential.
YES
NO
IMPORTANT!
A process during which there is no energy transfer by heat is called ADIABATIC
dtQQ
2
1
t
t
 

12
2
1
QQ 
12
2
1
QQQ  

11. 11
WORK (Energy transfer by work)
In thermodynamics work is a means for “transferring energy” and so in thermodynamics
energy is transferred and stored when work is done.
A closed system can interact with its surroundings and energy can cross its boundary (heat
and work).
Work in mechanics
The force applied to the body varies from position to position along the path
𝑊𝑜𝑟𝑘 = ∫ 𝐹⃗⃗⃗
2
1
∙ 𝑑𝑠⃗⃗⃗⃗
where ds is the body displacement along the path s.
To evaluate this integral we must know how the force varies by varying the displacement.
W depends on the interaction between the system and its surroundings along the path 1 --> 2
The symbol commonly used is W and the units are Joule.
The work transferred per unit mass is w (J/kg)
The mechanical power, is the work transferred per unit time Ẇ (W).
If Ẇ varies with time
Sign convention
W>0 Work transferred FROM the system to the surroundings
W<0 Work transferred FROM the surroundings to the system
Work is a quantity transferred between systems or between a system and its surroundings
and for this reason it is not a PROPERTY cause the amount of work exchanged depends
more than just on the state of the system.
YES
NO
dtWW
2
1
t
t
 

12
2
1
WWW  
12
2
1
WW 

12. 12
Expansion and compression work
o In the piston cylinder assembly there’s a gas
o The gas expands
o p is the average pressure at the piston face
o A is the piston section
o the force exerted F is --> F=p·A
The work done when the piston is displaced by dx is:
Which is the sign of W?
EXPANSION
The volume increases dV > 0 W>0
COMPRESSION
The volume decreases dV < 0 W<0
dxApW 
dVdxA 
dVpW 

13. 13
If the volume changes from the value V1 to V2
Work will be:
This equation is true and applicable for any system if the pressure is uniform with position
over the moving boundary (the relation between p and V is known)
Actual processes: Expansion and compression
In an actual cycle non equilibrium effects are present inside the cylinder and non-uniformities
give rise. It is not possible to find a relation between p and V and so the integral
cannot be calculated.
 
2
1
V
V
dVpW
 
2
1
V
V
dVpW

14. 14
Quasi equilibrium (static) processes
It’s a process that proceeds in such a manner that the system remains infinitesimally close to
an equilibrium state at all times
o departure from the equilibrium state is at most infinitesimal
o the system passes only through states that can be considered equilibrium states
o idealized process
o intensive properties are uniform all over the system at each state visited during
the transformation
o it is possible to find a relation between p and V and thus perform the previous
integral
STEP 1
System = a gas inside a cylinder
Initial state (equilibrium)
EQUILIBRIUM
The pressure exerted by the gas on the lower face of the piston is equal to the force due to
the masses placed on the piston.
STEP 2 (one small mass is removed)
 the gas pressure overcomes the external pressure
 the system expands and slightly departs from the equilibrium state
 after a short time a new equilibrium state is reached

15. 15
STEP 3…to…n
All the other masses are removed one at a time. If the masses are made vanishingly small the
process follows a series of equilibrium states
 system undergoes a quasi equilibrium process
 relationship between p and V can be find
Final state (equilibrium)
The relationship between p and V can be shown in a ( p,V ) diagram the Clapeyron diagram

16. 16
Some conclusions
NON EQUILIBRIUM PROCESSES
1) A relationship between p and V cannot be found
2) In a diagram
3) We cannot use the integral
4) The work W must be evaluated in another way
EQUILIBRIUM QUASISTATIC PROCESSES
1) A relationship between p and V can be found
2) In a diagram
3) We can use the integral
 
2
1
V
V
dVpW
 
2
1
V
V
dVpW

17. 17
Work is not a property its value depends on the path!
WA WB

18. 18
1st Law of Thermodynamics
The 1st
law of thermodynamics, also known as the conservation of energy principle, provides
a relationship among the different forms of energy.
The 1st
law states that:
“Energy can be neither created nor destroyed during a process, it can only change form.”
or
“The net change (increase or decrease) in the total energy of the system during a process is
equal to the difference between the total energy entering and the total energy leaving the
system during the process.”
Energy balance for closed systems
 A closed system exchanges energy through heat & work
 We must complied with the conservation of energy
𝐸2 − 𝐸1 = 𝑄 − 𝑊
E2-E1 = Change in the amount of energy contained within the system
Q = Net amount of energy transferred (in/out) across the system boundary by heat
W = Net amount of energy transferred (in/out) across the system boundary by work
∆( 𝐾𝐸) + ∆( 𝑃𝐸) + ∆𝑈 = 𝑄 − 𝑊
The instantaneous time rate form of the energy balance is:
WQdE  

 WQ
dt
dE

19. 19
The thermodynamic cycles
The energy balance for a thermodynamic cycle is:
 Ecycle=0; because E is a property
Qcycle ; Wcycle = Net amount of energy transferred (in/out) by heat and by work during the cycle
IMPORTANT !
If the cycle is composed by quasi static process the area of the cycle in the (p,v) diagram is
equal to the net work (heat) exchanged between the system and its surroundings
CYCLECYCLECYCLE WQE 

20. 20
ENERGY CONVERSION EFFICIENCY
The term efficiency indicates how well an energy conversion or transfer process is
accomplished. The most general definition is:
Performance=Desired output/ required input
We can apply this definition to different kind of cycle
We’ll refer to two general classes of cycles:
1) Direct cycles: POWER CYCLES = Power/work are developed
2) Inverse cycles: REFRIGERATION & HEAT PUMP CYCLES = Input of power/work is
required
Power cycles
Wcycle>0
Thermal efficiency:
 < 1
OUTINOUTINcycle QQQQW 
IN
cycle
Q
W

IN
OUT
IN
OUTIN
IN
cycle
Q
Q
1
Q
QQ
Q
W




21. 21
Refrigeration cycles
The task of a refrigeration cycle is to remove heat
from a body that is already cold
Wcycle<0
Coefficient of performance:
Heat pump cycles
The task of a heat pump cycle is to transfer heat from
a cold body to a hot one
Wcycle<0
Coefficient of performance:
OUTINOUTINcycle QQQQW 
OUTIN
IN
cycle
IN
QQ
Q
W
Q


OUTINOUTINcycle QQQQW 
OUTINcycle QQW 
OUTINcycle QQW 











1
QQ
Q
1
QQ
QQQ
QQ
Q
W
Q
OUTIN
IN
OUTIN
ININOUT
OUTIN
OUT
cycle
OUT