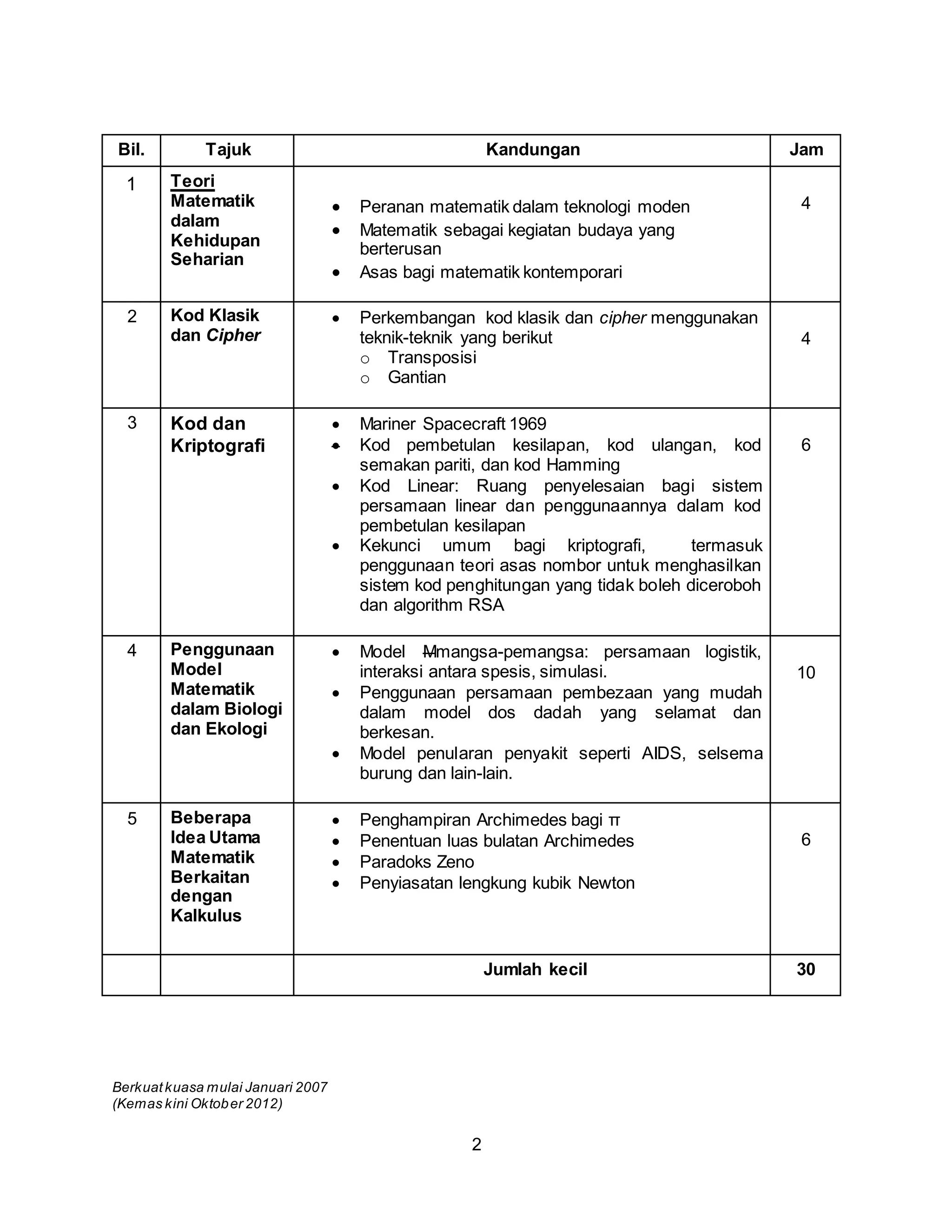
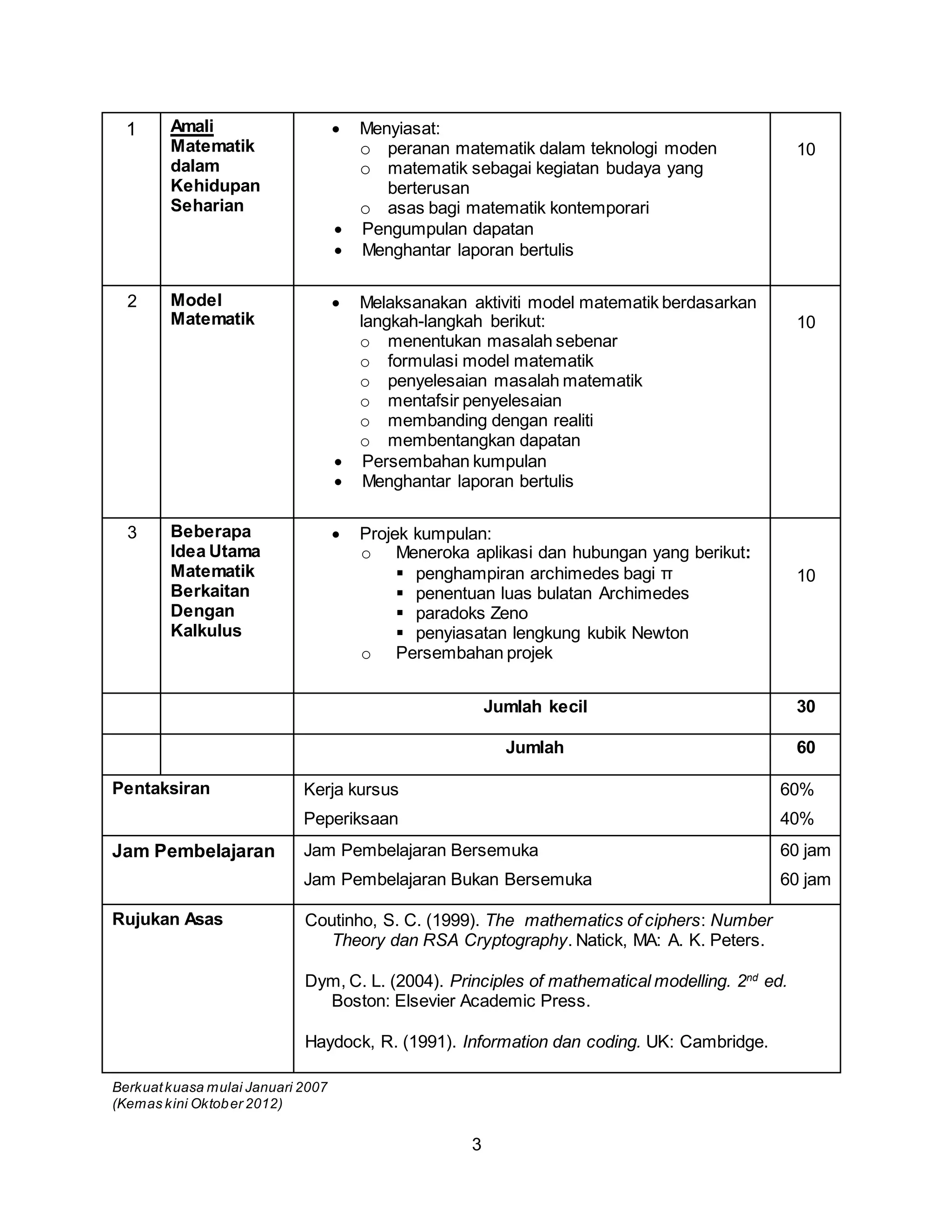
Kursus ini memberi tumpuan kepada aplikasi matematik dalam bidang biologi, ekologi, teknologi, dan kriptografi. Pelajar akan belajar tentang model matematik dalam biologi dan ekologi, kod klasik, kod dan kriptografi, serta idea matematik berkaitan kalkulus. Pengalaman aplikasi matematik akan diberikan melalui aktiviti praktikal seperti projek kumpulan.

1. Berkuatkuasa mulai Januari 2007
(Kemas kini Oktober 2012)
1
PRO FORMA KURSUS
PROGRAM IJAZAH SARJANA MUDAPERGURUAN DENGAN KEPUJIAN
(Matematik Pendidikan Rendah)
Tajuk Kursus Aplikasi Matematik
(Applications of Mathematics)
Kod Kursus MTE3114
Kredit 3(2+1)
Jam
Pembelajaran
120 Jam
Bahasa
Pengantar
Bahasa Melayu
Prasyarat Tiada
Semester Lapan
Hasil
Pembelajaran
1. Meneroka peranan matematik dalam teknologi moden.
2. Menyiasat matematik sebagai kegiatan budaya yang berterusan
3. Mendemonstrasikan kefahaman terhadap kod dan kriptografi
4. Mengaplikasi model matematik dalam Biologi dan Ekologi
5. Mendemonstrasikan kefahaman terhadap beberapa idea utama
matematik berkaitan dengan kalkulus
Sinopsis Kursus ini berfokus kepada aplikasi Matematik dalam pelbagai bidang. Isi
kandungannya meliputi Matematik dalam kehidupan harian, kod klasik
dan cipher, kod dan kriptografi, penggunaan model Matematik dalam
biologi dan ekologi, serta sebahagian idea utama Matematik berkaitan
dengan kalkulus. Pengalaman melibatkan aplikasi Matematik dibekalkan
melalui aktiviti-aktiviti praktikal.
This course focuses on the applications of Mathematics in various areas.
Its contents cover Mathematics in everyday life, classical codes and
ciphers, codes and cryptography, use of mathematical modeling in
biology and ecology, and some key mathematical ideas related to
calculus. Experience involving applications of Mathematics is provided
through practical activities.

2. Berkuatkuasa mulai Januari 2007
(Kemas kini Oktober 2012)
2
Bil. Tajuk Kandungan Jam
1 Teori
Matematik
dalam
Kehidupan
Seharian
 Peranan matematik dalam teknologi moden
 Matematik sebagai kegiatan budaya yang
berterusan
 Asas bagi matematik kontemporari
4
2 Kod Klasik
dan Cipher
 Perkembangan kod klasik dan cipher menggunakan
teknik-teknik yang berikut
o Transposisi
o Gantian
4
3 Kod dan
Kriptografi
 Mariner Spacecraft 1969
 Kod pembetulan kesilapan, kod ulangan, kod
semakan pariti, dan kod Hamming
 Kod Linear: Ruang penyelesaian bagi sistem
persamaan linear dan penggunaannya dalam kod
pembetulan kesilapan
 Kekunci umum bagi kriptografi, termasuk
penggunaan teori asas nombor untuk menghasilkan
sistem kod penghitungan yang tidak boleh diceroboh
dan algorithm RSA
6
4 Penggunaan
Model
Matematik
dalam Biologi
dan Ekologi
 Model Mmangsa-pemangsa: persamaan logistik,
interaksi antara spesis, simulasi.
 Penggunaan persamaan pembezaan yang mudah
dalam model dos dadah yang selamat dan
berkesan.
 Model penularan penyakit seperti AIDS, selsema
burung dan lain-lain.
10
5 Beberapa
Idea Utama
Matematik
Berkaitan
dengan
Kalkulus
 Penghampiran Archimedes bagi π
 Penentuan luas bulatan Archimedes
 Paradoks Zeno
 Penyiasatan lengkung kubik Newton
6
Jumlah kecil 30

3. Berkuatkuasa mulai Januari 2007
(Kemas kini Oktober 2012)
3
1 Amali
Matematik
dalam
Kehidupan
Seharian
 Menyiasat:
o peranan matematik dalam teknologi moden
o matematik sebagai kegiatan budaya yang
berterusan
o asas bagi matematik kontemporari
 Pengumpulan dapatan
 Menghantar laporan bertulis
10
2 Model
Matematik
 Melaksanakan aktiviti model matematik berdasarkan
langkah-langkah berikut:
o menentukan masalah sebenar
o formulasi model matematik
o penyelesaian masalah matematik
o mentafsir penyelesaian
o membanding dengan realiti
o membentangkan dapatan
 Persembahan kumpulan
 Menghantar laporan bertulis
10
3 Beberapa
Idea Utama
Matematik
Berkaitan
Dengan
Kalkulus
 Projek kumpulan:
o Meneroka aplikasi dan hubungan yang berikut:
 penghampiran archimedes bagi π
 penentuan luas bulatan Archimedes
 paradoks Zeno
 penyiasatan lengkung kubik Newton
o Persembahan projek
10
Jumlah kecil 30
Jumlah 60
Pentaksiran Kerja kursus
Peperiksaan
60%
40%
Jam Pembelajaran Jam Pembelajaran Bersemuka
Jam Pembelajaran Bukan Bersemuka
60 jam
60 jam
Rujukan Asas Coutinho, S. C. (1999). The mathematics of ciphers: Number
Theory dan RSA Cryptography. Natick, MA: A. K. Peters.
Dym, C. L. (2004). Principles of mathematical modelling. 2nd
ed.
Boston: Elsevier Academic Press.
Haydock, R. (1991). Information dan coding. UK: Cambridge.

4. Berkuatkuasa mulai Januari 2007
(Kemas kini Oktober 2012)
4
Stacey, K. & Stillman, G. (2002). Modelling trends in number of
deaths due to HIV/AIDS infection in USA dan Australia.
Melbourne: University of Melbourne, CAS-CAT Project.
Wilf, H. S. (1986). Algorithms dan complexity. Englewood Cliffs, NJ:
Prentice-Hall.
Rujukan Tambahan Fazekas de St Groth, C., & Solomon, P. J. (1990). Short-term
prediction of the AIDS epidemic using empirical models. In P. J.
Solomon, C. Fazekas de St Groth, & S. R. Wilson (Eds.),
Projections of acquired immune deficiency syndrome in Australia
using data to the end of September 1989 (Working Paper No. 16,
pp. 11-17). Canberra, ACT: Australian National University,
National Centre for Epidemiology dan Population Health.
Full Singh, S. (2002). The cracking codebook: How to make it, break
it, hack it, crack it. London: Harper Collins.
Hellman, M. E. (1979). The mathematics of public-key cryptography.
Scientific American, 241(8), 146–157.
Humphreys, J. F., & Prest, M. Y. (2004). Numbers, groups dan
codes. 2nd
ed. Cambridge: Cambridge University Press.
Jackson, M. B., & Ramsey, J. R. (1993). Problems for student
investigation. MAA Notes. Volume 30. Washington: Mathematical
Association of America.
Jackson, T. H. (1987). From nombor theory to secret codes. Bristol:
IOP Publishing.
Malevitch, J., Froelich, G., & Froelich, D. (1991). Codes galore
Module #18. Lexington, VA: Consortium for mathematics dan Its
Applications (COMAP).
Maynard Smith, J. (1968). Mathematical ideas in biology. London:
Cambridge University Press.
Posamentier, A. A., & Lehmann, I. (2004). π: A biography of the
world's most mysterious nombor, Amherst, NY: Prometheus
Books.
Trappe, W., & Washington, L. C. (2006). Introduction to cryptography
with coding theory. 2nd
ed. Upper Saddle River, NJ: Pearson
Prentice Hall.
Welsh, D. J. A., (1988). Codes dan cryptography. Oxford: Oxford
University Press.