Las leyes de la Gravitacion
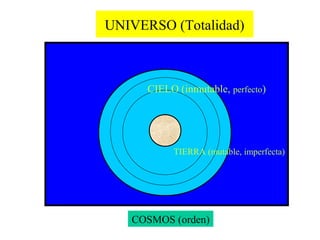
- 1. UNIVERSO (Totalidad) CIELO (inmutable, perfecto) TIERRA (mutable, imperfecta) COSMOS (orden)
- 2. TIPOS DE INTERACCIONES NOMBRE VALOR RELATIVO ÁMBITO DE MANIFESTACIÓN NUCLEAR FUERTE 1 Entre protones- neutrones ELECTRO- MAGNÉTICA 10-2 entre cargas NUCLEAR DÉBIL 10-12 en desintegraciones nucleares GRAVITATORIA 10-38 entre masas
- 5. EPICICLOS EPICICLO DEFERENTE
- 6. MODELO DE COPÉRNICO NICOLÁS COPÉRNICO Thorn (Polonia) 1473-1543
- 7. MODELO DE TYCHO BRAHE TYCHO BRAHE (1546-1601) Knudstrup, Escania; hoy Suecia Apreciése su nariz ortopédica de oro
- 8. LEYES DE KEPLER JOHANNES KEPLER Weilderstadt (1571- 1630) Modelo cósmico de Kepler basado en los sólidos platónicos
- 9. PRIMERA LEY Los planetas describen órbitas elípticas estando el Sol en uno de sus focos. •Semieje mayor a AFELIO • Semieje menor b •Semidistancia focal c • La relación entre los semiejes es a2=b2+c2 • La excentricidad se define como el cociente e=c/a PERIHELIO
- 10. SEGUNDA LEY El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales. t A A t
- 11. LEY DE LAS ÁREAS L r + dr dS r dr Como el planeta se ve sometido a una fuerza central su Momento Angular L será constante entonces: 1 dS = r ×dr 2 dr m L = m ⋅ r ×v = m ⋅ r × = r ×dr dt dt 2mdS dS L = = 2m ⇒ dt dt dS L = = CONSTANTE dt 2m
- 12. TERCERA LEY Los cuadrados de los periodos de revolución son proporcionales a los cubos de los semiejes mayores de la elipse. T2 = k r 3
- 13. Ley de Gravitación Universal Un planeta de masa m que gira alrededor del sol en un tiempo T describiendo una órbita de radio R está sometido a una fuerza normal: v2 v2 an = F = m R R 2 πR Suponiendo que la órbita es circular v = T 4π 2 R 2 R F = m = 4π 2 m 2 T 2R T Según la tercera ley de Kepler. Entonces R 4π 2 1 m F = 4π 2 m = m 2 = KP 2 kR 3 k R R
- 14. LEY DE NEWTON ISAAC NEWTON (1643-1727)
- 15. Ley de Gravitación Universal El Sol estará sometido a una fuerza igual y de sentido contrario M m F = KS 2 = KP 2 R R KS M = KP m KS KP = = G m M M⋅m resultando entonces F= G o en forma vectorial R2 M⋅m F = −G ⋅ ur G= 6.67·10-11 N·m2·kg-2 R 2
- 16. Energía Potencial Gravitatoria Si calculamos el trabajo realizado por la fuerza de gravedad cuando una masa m pasa de un punto A otro B en el campo creado por otra masa M. BM⋅m W = ∫A − G 2 u ⋅ d r r Cualquier desplazamiento dr se puede descomponer en dos vectores, uno paralelo a r y otro perpendicular a él, que por serlo nunca realiza trabajo. Entonces podemos escribir B M⋅m W= ∫A − G r 2 ⋅ dr B 1 W = GM ⋅ m ∫A − r 2 ⋅ dr B 1 GM ⋅ m GM ⋅ m W = GM ⋅ m = − r A rB rA
- 17. ENERGÍA POTENCIAL GRAVITATORIA Vemos que el trabajo depende de una cantidad evaluada en los puntos inicial y final, y no del camino recorrido. Se trata pues de una fuerza conservativa a la que se puede asociar una energía potencial: W = − ∆ E = EPA − EPB GM ⋅ m GM ⋅ m W=− − − rA rB Por tanto la ENERGÍA POTENCIAL GRAVITATORIA viene dada por la expresión: GM ⋅m EP = − r
- 18. ENERGÍA MECÁNICA Ep r M⋅m EP = −G r La Energía Mecánica será la suma de la E. Cinética de la masa y de su E. Potencial. En ausencia de otras fuerzas es constante 1 M⋅m EM = EC + EP = mv − G 2 2 r
- 19. RELACIÓN ENTRE LA ENERGÍA TOTAL Y LA TRAYECTORIA EN EL MOVIMIENTO BAJO UNA FUERZA GRAVITATORIA EM = 0 EM < 0 r r r EM < 0 Ec Ec Ec Ep Ep Ep ELIPSE PARÁBOLA HIPÉRBOLA
- 20. TRAYECTORIAS DE UNA PARTÍCULA LANZADA HORIZONTALMENTE DESDE UNA ALTURA h v0 h E > 0 Hipérbola R E = 0 Parábola E < 0 Elipses
- 21. LÍNEAS DE CAMPO GRAVITATORIOY SUPERFICIES EQUIPOTENCIALES DEL SISTEMA TIERRA-LUNA
- 22. VARIACIÓN DEL CAMPO GRAVITATORIO EN UNA ESFERA MACIZA g (m/s2) 9,8 RT r
Editor's Notes
- KJLK
