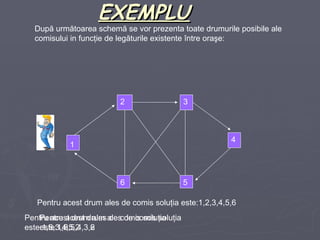
Documentul descrie problema comis-voiajorului, care trebuie să viziteze un număr de orașe fără a repeta niciunul, întorcându-se la orașul inițial. Se detaliază algoritmul pentru generarea tuturor drumurilor posibile elaborate pe baza unei matrice simetrice de legături între orașe. Observațiile includ restricții privind validitatea succesorilor în cadrul stivei utilizate pentru a rezolva această problemă.

1. Problema comis-voiajorului S îrca Victor

2. Enunţul problemei Un comis - vo iajor trebuie să viziteze un număr de n oraşe. Iniţial acesta se află într-unul dintre ele notat cu 1. Acesta doreşte să nu treacă prin acelaşi oraş de 2 ori, iar la întoarcere să revină în oraşul 1. Cunoscând legăturile existente între oraşe, să se tipărească toate drumurile posibile pe care le poate efectua comisul.

3. EXEMPLU 1 2 3 4 5 6 Pentru acest drum ales de comis soluţia este :1,2,3,4,5,6 Pentru acest drum ales de comis solu ţ ia este: 1,2,5,4,3,6 Pentru acest drum ales de comis soluţia este :1,6,3,4,5,2 Pentru acest drum ales de comis solu ţ ia este:1,6,5,4,3,2 După următoarea schemă se vor prezenta toate drumurile posibile ale comisului in funcţie de legăturile existente între oraşe :

4. ALGORITMUL Pentru rezolvarea problemei vom avea nevoie de o matrice pătratică simetrică, de o stivă(st) la baza căreia la nivelul 1 se găseşte numărul 1 1 2

5. Algoritmul continuă până se ajunge din nou la nivelul 1 caz în care algoritmul se încheie. OBSERVAŢII un succesor între 2 si n aflat pe nivelul k este considerat valid dacă : Nu s-a mai trecut prin oraşul simbolizat de succesor deci acesta nu se găseşte in stivă Există drum între oraşul aflat pe nivelul k-1 şi oraşul aflat pe nivelul k Când stiva ajunge la nivelul k=n să existe drum de la oraşul acesta la oraşul 1

6. PROGRAMUL Program comis ; Type stiva=array[1..100]of integer; mat:array[1..6,1..6] of integer; Var Procedure init(k:integer;var st:stiva); Begin st[k]:=1; End; Procedure succesor(var as:boolean;var st:stiva;k:integer); Begin for i:=1 to n do if st[k]<n then begin as:=true; st[k]:=st[k]+1; end else asL=false; End; Procedure valid(var ev:boolean;st:stiva;k:integer); Begin if a[st[k-1],st[k]]=0 then ev:=false else for i:=1 to k-1 do if st[i]=st[k] then ev:=false else if (k=n) and(a[1,st[k]=0) then ev:=false; End; Procedure tipar; Begin for i:=1 to n do write(st[i]); End; Begin Write(‘n=‘); readln(n); For i:=1 to n do for j:=1 to i-1 do begin Write(‘a[‘,I,’ ‘,j,’]=‘); readln(a[I,j]); a[j,i]:=a[i,k]; End; St[1]:=1; K:=2; While k>1 do begin repeat succesor(as,st,k); if as then valid(ev,st,k); Until (not as) or (as and ev); If as then If solutie(k) then tipar else begin k:=k+1; init(k,st); end else k:=k-1; End; Readln; END.