1. 4.2 Mean Value Theorem

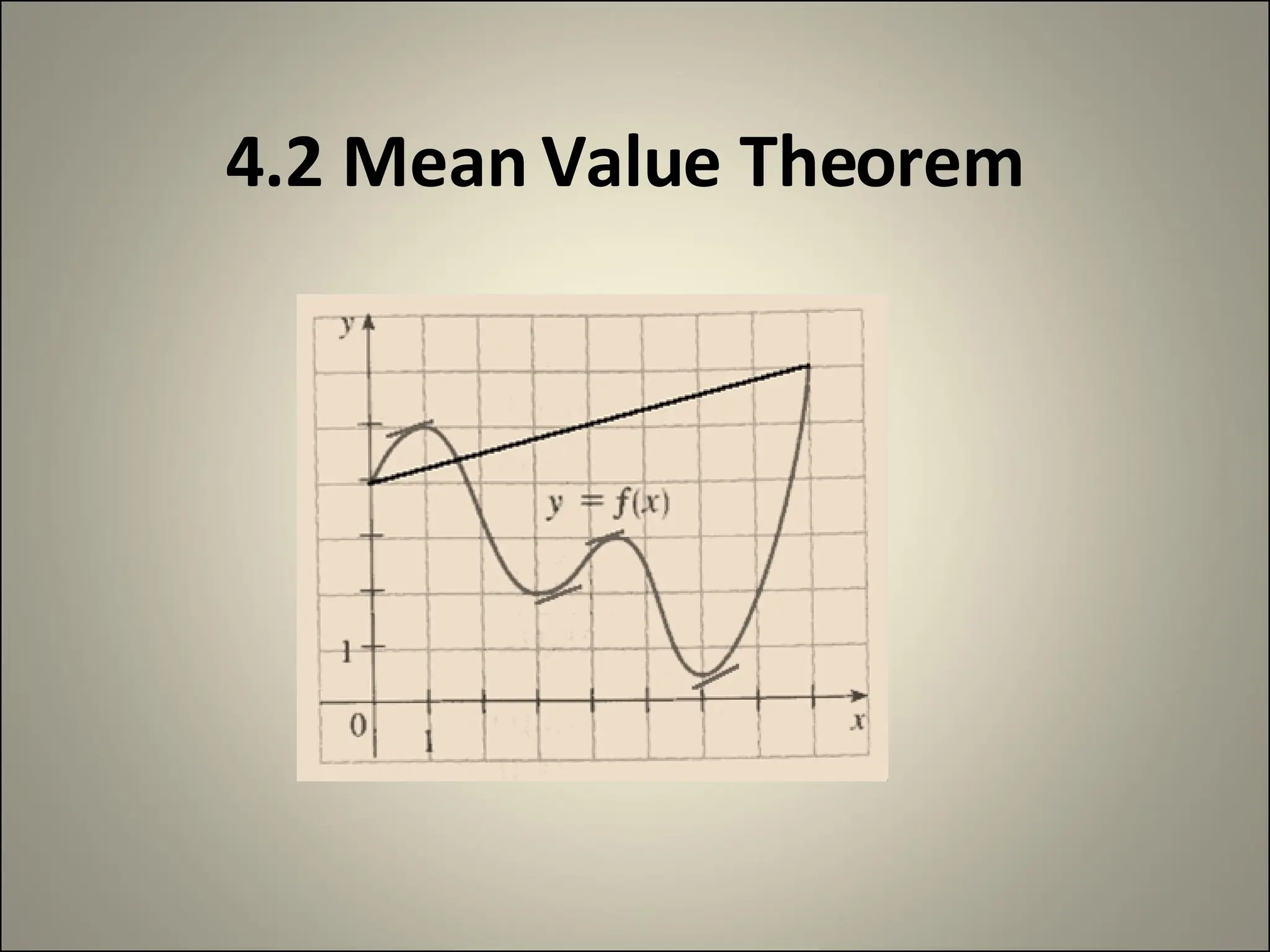
2. Mean Value Theorem for Derivatives If y = f(x) is continuous at every point of the closed interval [a,b] and differentiable at every point of its interior (a,b) then there is at least one point c in (a,b) at which

3. Using Mean Value Theorem Show that f(x) = 2x 2 satisfies the mean value theorem on the interval [0,2]. Then find the solution to the equation on the interval. Find f’(x) f’(x) = 4x 4 = 4x X= 1

4. Using Mean Value Theorem f(x) = l x – 1 l on [0, 4] f(a) = -1 f(b) = 3 1 = l x -1 l The function does not satisfy the mean value theorem because there is a cusp so the function is not continuous on [0,4]

5. Mean Value Theorem f(x) = -2x 3 + 6x – 2 , [-2 , 2] f(-2) = -2(-2) 3 + 6(-2) - 2 = 2 f(2) = -2(2) 3 + 6(2) - 2 = - 6 f(x) = -6 - 2 = -2 2 - (-2) f '(x) = -6x 2 + 6 -2 = -6x 2 + 6 X = 2 -2 √3, √3 Mean value is satisfied because the function is continuous on [-2, 2]

6. Using Mean Value Theorem f(x) = x 3 + 3x – 1, [0,1] f(b) = 3 f(a) = -1 f’(x) = 3x 2 + 3 4 = 3x 2 +3 X =

7. Mean Value with Trig. Functions

8. More mean value Solve.