Biomedical engineering mathematics i

جامعة المنيا كلية الهندسة
قسم هندسة القوى الميكانيكية والطاقة
Start
Engineering Mathematics I
2014/2015
1 12/3/2014

Start
This programme unit aims to: The programme unit aims to
provide a basic course in calculus, algebra, and numerical analysis
to be used in BME to students with A-level mathematics.
Prerequisite knowledge: Knowledge of Integration, Differentiation,
Microsoft Office Excel is required for taking this programme unit
2 12/3/2014

Start
General &
Transferable
Practical &
Professional
Intellectual
Knowledge &
Understanding
a1- Define the concepts related to Engineering Mathematics
a2- Specify the different applications of differential equations, Fourier series,
combinations and Interpolation.
a3- Discuss solving the DE with series, and special functions
a4- Distinguish between ODE and linear DE.
c1- Merge the engineering knowledge and understanding to model different
Biomedical systems.
c2- Relate solution of DE to real life problems .
b1- Analyse different systems using DE
b2- Select the suitable method to solve a DE system
b3- Apply the interpolation to curve fitting
b4- Represent different functions with Fourier series
d1- Communicate effectively using written, oral
d2- Use information technology, IT, effectively
3 12/3/2014
The Intended Learning Outcomes; ILO’s

Start
List of Topics
Topic 01 • Multiple, line and surface integrals
Topic 02 • Partial differentiation and application
Topic 03 • Infinite Series
Topic 04 • Power Series
Topic 05 • Fourier Series
Topic 06 • Higher degrees First Order ODE and applications
Topic 07 • Linear DE and applications
Topic 08 • Combinations and Curves Interpolation
Topic 09 • Series solution of DE
Topic 10 • Special Functions
4 12/3/2014

Start
References
• Advanced Engineering Mathematics, Erwin Kreyszig, 9th Edition,
• Thomas' Calculus: Early Transcendentals: Media Upgrade. Weir,
M.D., et al., 2008: Pearson Addison-Wesley.
References to chapters will be given from time to time
Student is required to search and read any other books or websites
related to the subjects introduced
5 12/3/2014

Start
Teaching and
Learning
Methods
• Lectures.
• Office hours
• Team work.
• Self learning
Students
Assessment
Methods and
Schedule
• Tutorial (every week)
• Reports (scheduled by instructors)
• Written mid-term exam (Week# 8 or 9 )
• Written final exam (Scheduled by the Faculty Council)
Weighing of
assessments
Methods
• Semester work (Tutorial and Reports) 20 %
• Written mid-term exam 20 %
• Written final exam 60 %
• Total 100 %
6 12/3/2014

Start
1
• Multiple Integrals
2
• Line Integrals
3
• Surface Integrals
Topic 1: Multiple, line and surface integrals
7 12/3/2014

Start
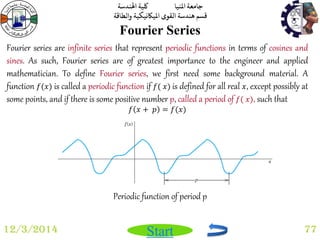
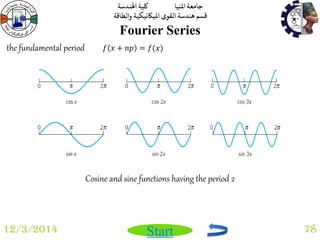
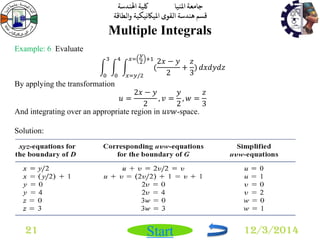
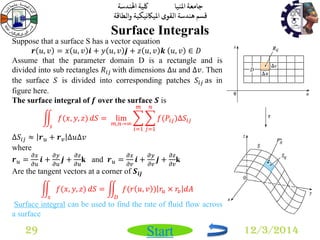
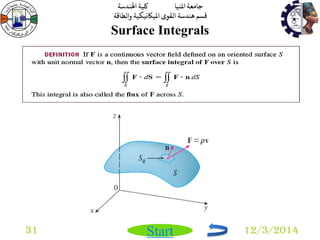
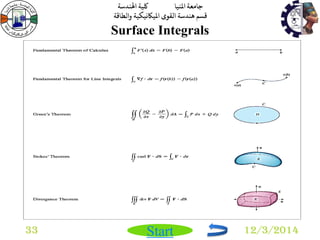
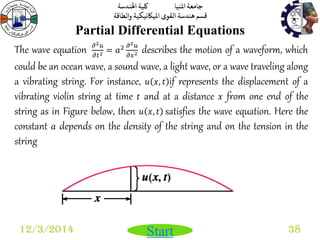
Multiple Integrals
8 12/3/2014
Integration
Another basic concept of calculus that will be used extensively is the
Riemann integral.
The Riemann integral of the function
푓 on the interval [푎, 푏] is the
following limit
푓 푥
푏
푎
푑푥 = lim
푚푎푥Δ푥푖⟶0
푓 푧푖 Δ푥푖 ,
푛
푖=1
Where the numbers 푥0, 푥1, …….., 푥푛
satisfy 푎 = 푥0 ≤ 푥1 ≤ …. ≤ 푥푛 = 푏 ,
where Δ푥푖 = 푥푖 −푥푖−1 , for each
푖 = 1,2, … . , 푛, and 푧푖 is an arbitrarily
chosen in the interval [푥푖−1,푥푖].
Def. 1 Fig. 1

Start
Multiple Integrals
9 12/3/2014
The additivity property for rectangular
regions holds for regions bounded by
continuous curves

Start
Multiple Integrals
10 12/3/2014

Start
Multiple Integrals
11 12/3/2014

Start
Multiple Integrals
12 12/3/2014

Start
Multiple Integrals
13 12/3/2014
Exercise A

Start
Multiple Integrals
14 12/3/2014
Applications

Start
Multiple Integrals
15 12/3/2014
Example: 3
A thin plate covers the triangular region bounded by the x-axis and the lines x=1 and y=2x
in the first quadrant. The plate’s density at the point (x,y) is δ(x, y) = 6x + 6y + 6 find the
plate’s mass, first moments, and centre of mass about the coordinate axes

Start
Multiple Integrals
16 12/3/2014

Start
Multiple Integrals
17 12/3/2014
Example: 4
For the thin plate given in example 3 find the moments of inertia and radii of gyration about
the coordinate axes and the origin.

Start
Multiple Integrals
18 12/3/2014
Triple integral
D
D
D
5 D

Start
Multiple Integrals
19 12/3/2014
Triple integral applications

Start
Multiple Integrals
20 12/3/2014

Start
Multiple Integrals
21 12/3/2014
Example: 6 Evaluate
(
2푥 − 푦
2
+
푧
3
)
푥=
푦
2
+1
푥=푦/2
4
0
3
0
푑푥푑푦푑푧
By applying the transformation
푢 =
2푥 − 푦
2
, 푣 =
푦
2
, 푤 =
푧
3
And integrating over an appropriate region in 푢푣푤-space.
Solution:

Start
Multiple Integrals
22 12/3/2014

Start
Line Integrals
23 12/3/2014
Suppose that 푓(푥, 푦, 푧) is a real-valued function and we
wish to integrate it over the curve 풓 푡 = 푔 푡 풊 + 푕 푡 풋
+ 푘 푡 풌, 푎 ≤ 푡 ≤ 푏 (shown in the figure)
The line integral of 푓 over 퐶 is
푓 푥, 푦, 푧
퐶
푑푠
If 풓 푡 is smooth for 푎 ≤ 푡 ≤ 푏 ( 푣 = 푑풓/푑푡 is
continuous and never 0), then the length of the curve C
can be calculated by
푠 푡 = 퐯(휏)
푏
푎
푑휏
Then the integral of 푓 over 퐶 can be written as
푓 푥, 푦, 푧
퐶
푑푠 = 푓(푔 푡 , 푕 푡 , 푘 푡 )
푏
푎
퐯(푡) 푑푡
Line integral can be used to find the work done by a
force field in moving an object along a curve

Start
Line Integrals
24 12/3/2014

Start
Line Integrals
25 12/3/2014
Example: 7 Integrate 푓 푥, 푦, 푧 = 푥 − 3푦2 + 푧 over the line segment C joining the origin
to the point (1,1,1).

Start
Line Integrals
26 12/3/2014
Example: 8 Evaluate 2푥 푐 푑푠, where C consists of the arc 퐶1 of the parabola 푦 = 푥2 from
(0,0) to (1,1) followed by the vertical line segment 퐶2 from (1,1) to (2,2).
8
8

Start
Line Integrals
27 12/3/2014

Start
Multiple Integrals
28 12/3/2014
إليكم أربعة عشر فرقًا يميز تفكير الناجح عن تفكير الفاشل، أدعوكم إلى التأمل فيها بعمق ثم إلى تغيير نمط تفكيركم،
لينسجم مع تفكير الناجحين وليتنافر مع تفكير الفاشلين:
1. الناجح يفكر في الحل، والفاشل يفكر في المشكلة.
2. الناجح لا تنضب أفكاره، والفاشل لا تنضب أعذاره.
3. الناجح يساعد الآخرين، والفاشل يتوقع المساعدة من الآخرين.
4. الناجح يرى حل ا في كل مشكلة، والفاشل يرى مشكلة في كل حل.
5. الناجح يقول: "الحل صعب لكنو ممكن" والفاشل يقول: "الحل ممكن ولكنو صعب".
6. الناجح يعتبر الإنجاز التزااما يلبيو، والفاشل لا يرى في الإنجاز أكثر من وعد يعطيو.
7. الناجح لديو أحلم يحققها، والفاشل لديو أوىام وأضغاث أحلم يبددىا.
8. الناجح يقول: "عامل الناس كما تحب أن يعاملوك، والفاشل يقول : اخدع الناس قبل أن يخدعوك.
9. الناجح يرى في العمل أمل، والفاشل يرى في العمل ألم.
10 .الناجح ينظر للمستقبل ويتطلع لما ىو ممكن، والفاشل ينظر للماضي ويتطلع لما ىو مستحيل.
11 .الناجح يختار ما يقول، والفاشل يقول دون أن يختار.
12 .الناجح يناقش بقوة وبلغة لطيفة، والفاشل يناقش بضعف وبلغة فظة.
13 .الناجح يتمسك بالقيم ويتنازل عن الصغائر، والفاشل يتشبث بالصغائر ويتنازل عن القيم.
14 .الناجح يصنع الأحداث، والفاشل تصنعو الأحداث.
ىذه ىي صفات الفاشلين.. تعلمها ولكن لا تمارسها.

Start
Surface Integrals
29 12/3/2014
Suppose that a surface S has a vector equation
풓 푢, 푣 = 푥 푢, 푣 풊 + 푦 푢, 푣 풋 + 푧 푢, 푣 풌 푢, 푣 ∈ 퐷
Assume that the parameter domain D is a rectangle and is
divided into sub rectangles 푅푖푗 with dimensions Δ푢 and Δ푣. Then
the surface 푆 is divided into corresponding patches 푆푖푗 as in
figure here.
The surface integral of 풇 over the surface 푺 is
푓(푥, 푦, 푧)
푠
푑푆 = lim
푚,푛→∞
푓(푃푖푗 )Δ푆푖푗
푛
푗=1
푚
푖=1
Δ푆푖푗 ≈ 풓푢 + 풓푣 Δ푢Δ푣
where
풓푢 =
휕푥
휕푢
풊 +
휕푦
휕푢
풋 +
휕푧
휕푢
k and 풓푢 =
휕푥
휕푣
풊 +
휕푦
휕푣
풋 +
휕푧
휕푣
k
Are the tangent vectors at a corner of 푺풊풋
푓(푥, 푦, 푧)
푠
푑푆 = 푓(푟 푢, 푣 ) 푟푢 × 푟푣 푑퐴
퐷
Surface integral can be used to find the rate of fluid flow across
a surface

Start
Surface Integrals
30 12/3/2014
Example: 9 compute the surface integral 푥2
푠 푑푆, where 푆 is the unit sphere
푥2 + 푦2 + 푧2 = 1.

Start
Surface Integrals
31 12/3/2014

Start
Surface Integrals
32 12/3/2014
Example: 9 Find the flux of
the vector field 푭 푥, 푦, 푧
= 푧풊 + 푦풋 + 푥풌
Across the unit sphere
푥2 + 푦2 + 푧2 = 1.

Start
Surface Integrals
33 12/3/2014

Start
Partial differentiation and application
34 12/3/2014
Let 푓(푥, 푦) be a function with two variables. If we keep 푦 constant and
differentiate 푓 (assuming 푓 is differentiable) with respect to the variable 푥,
we obtain what is called the partial derivative of 푓 with respect to 푥 which is
denoted by
휕푓
휕푥
= 푓푥 = lim
ℎ→0
푓 푥 + 푕, 푦 − 푓(푥, 푦)
푕
Similarly if we keep 푥 constant and differentiate 푓 (assuming 푓 is
differentiable) with respect to the variable 푦, we obtain what is called
the partial derivative of 푓 with respect to 푦 which is denoted by
휕푓
휕푦
표푟푓푦 = lim
푘→0
푓 푥, 푦 + 푘 − 푓(푥, 푦)
푘

Start
Partial differentiation and application
35 12/3/2014
Example 10: Find the partial derivatives 푓푥 and 푓푥 if 푓(푥 , 푦) is given by
1. 푓 푥, 푦 = 푥2푦 + 2푥 + 푦
2. 푓 푥, 푦 = 푠푖푛 푥푦 + 푐표푠 푥
3. 푓 푥, 푦 = 푥푒푥푦
4. 푓 푥, 푦 = ln(푥2 + 2 푦)
5. 푓 푥, 푦 = 푦푥2 + 2 푦
6. 푓 푥, 푦 = 푥푒푥 + 푦
7. 푓(푥, 푦) = ln(2푥 + 푦푥)
8. 푓(푥, 푦) = 푥sin (푥 − 푦)
Example 11: Find the second partial derivatives 푓푥푥, 푓푥푦, 푓푦푥, and 푓푦푦 if
푓 푥 , 푦 = 푥3 + 푥2푦3 − 2푦2

Start
Partial Differential Equations
12/3/2014 36
Partial derivatives occur in partial differential equations that express certain
physical laws.
For instance, the partial differential equation
휕2푢
휕푥2 +
휕2푢
휕푥2 = 0
is called Laplace’s equation after Pierre Laplace (1749–1827). Solutions of this
equation are called harmonic functions ; they play a role in problems of heat
conduction, fluid flow, and electric potential.

Start
12/3/2014 37
Example 12: Show that the function 푢(푥, 푦) = 푒푥 sin 푦 is the solution of the
Laplace’s equation.

Start
12/3/2014 38
The wave equation
휕2푢
휕푡2 = 푎2 휕2푢
휕푥2 describes the motion of a waveform, which
could be an ocean wave, a sound wave, a light wave, or a wave traveling along
a vibrating string. For instance, 푢 푥, 푡 if represents the displacement of a
vibrating violin string at time 푡 and at a distance 푥 from one end of the
string as in Figure below, then 푢 푥, 푡 satisfies the wave equation. Here the
constant 푎 depends on the density of the string and on the tension in the
string

Start
12/3/2014 39
Example 13: verify that the function 푢(푥, 푡) = sin(푥 − 푎푡) satisfies the wave
equation.

Start
12/3/2014 40
Exercises:
1. Use the definition of partial derivatives as limits to find 푓푥 푥, 푦 and
푓푦 푥, 푦 .
푓 푥, 푦 = 푥푦2 − 푥3푦
푓 푥, 푦 = 푥 (푥 + 푦2)
2. Verify that the function 푢 =
1
푥2+푦2+푧2 is a solution of the three-dimensional
Laplace equation 푢푥푥 + 푢푦푦 + 푢푧푧 = 0
3. Verify that the function 푧 = ln(푒푥 + 푒푦) is a solution of the differential
equations 휕푧
휕푥
+
휕푧
휕푦
= 1 and 휕2푧
휕푥2
휕2푧
휕푦2 −
휕2푧
휕푥휕푦
2
= 0

Start
Infinite Series
12/3/2014 41
A sequence can be thought of as a list of numbers written in a definite
order:
푎1, 푎2, 푎3, 푎4, … , 푎푛, … = 푎푛
∞
The number 푎1 is called the first term, 푎2 is the second term, and in general
푎푛 is the nth term. We will deal exclusively with infinite sequences and so
each term 푎푛 will have a successor 푎푛+1.
If we try to add the terms of an infinite sequence 푎푛
∞ we get as expression
of the form 푎1 + 푎2 + 푎3 + 푎4 + ⋯ + 푎푛 + ⋯ which is called an infinite
series or just a series and is donated, for short, by the symbol 푎푛
∞푛
=1 or
푎푛.
1
2푛
∞
푛=1
=
1
2
+
1
4
+
1
8
+
1
16
+ ⋯ +
1
2푛 + ⋯ = 1

Start
Infinite Series
12/3/2014 42
Convergent and Divergent series:

Start
Infinite Series
12/3/2014 43

Start
Infinite Series
12/3/2014 44
Example 14: Find the sum of the geometric series
5 −
10
3
+
20
9
−
40
27
+ ⋯

Start
Infinite Series
12/3/2014 45
Example 15: Is the series 22푛31−푛 ∞푛
=1 convergent or divergent?

Start
Infinite Series
12/3/2014 46
Example 16: Find the sum of the series 푥푛 ∞푛
=0 , where 푥 < 1.

Start
Infinite Series
12/3/2014 47
Theorems

Start
Infinite Series
12/3/2014 48
Theorems

Start
Infinite Series
12/3/2014 49
Theorems

Start
Infinite Series
12/3/2014 50
Theorems

Start
Infinite Series
12/3/2014 51
Examples
Example 17: show that the series (
1
푛 푛+1
) ∞푛
=1 is convergent and find its sum.

Start
Infinite Series
12/3/2014 52
Examples
So the series is convergent and
Hence, the summation
Example 18: Find the sum of the series (
3
푛 푛+1
+
1
2푛) ∞푛
=1 .

Start
Infinite Series
12/3/2014 53
STRATEGY FOR TESTING SERIES
Several ways to examine the convergence and divergence of series; the problem is to decide
which test to use on which series. There are no hard and fast rules about which test to
apply to a given series, but you may find the following advice of some use.
The main strategy is to classify the series according to its form.
1. If the series is of the form 1
푛푃, it is a P-series, which we know to be convergent if
푃 > 1 and divergent if 푃 ≤ 1 .
2. If the series has the form 푎푟푛−1or 푎푟푛, it is a geometric series, which converges if
푟 < 1 and diverges if 푟 ≥ 1 . Some preliminary algebraic manipulation may be
required to bring the series into this form.

Start
Infinite Series
12/3/2014 54
3. If the series has a form that is similar to a P-series or a geometric series, then one of
the comparison tests should be considered. In particular, if 푎푛 is a rational function
or an algebraic function of (involving roots of polynomials), then the series should be
compared with a P-series. The comparison tests apply only to series with positive
terms, but if 푎푛has some negative terms, then we can apply the comparison test to
푎푛 and test for absolute convergence.
4. If you can see at a glance that lim
푛→∞
푎푛 ≠ 0, then the Test for Divergence should be
used.
5. If the series is of the form (−1)푛−1 푏푛 or (−1)푛 푏푛, then the Alternating Series
Test is an obvious possibility.
6. Series that involve factorials or other products (including a constant raised to the nth
power) are often conveniently tested using the Ratio Test. Bear in mind that
푎푛+1
푎푛 → 1 as 푛 → ∞ for all p-series and therefore all rational or algebraic
functions of n. Thus the Ratio Test should not be used for such series.

Start
Infinite Series
12/3/2014 55
7. If 푎푛 is of the form (푏푛)푛, then the Root Test may be useful.
8. If 푎푛 = 푓(푛) , where 푓(푥)
∞
1 푑푥 is easily evaluated, then the Integral Test is effective
(assuming the hypotheses of this test are satisfied).

Start
Infinite Series
12/3/2014 56
Exercise
Determine whether the series is convergent or divergent. If it is convergent, find its sum.
1. 1
2푛
∞푛
=1 2. 푛+1
2푛−3
∞푛
=1 3. 푘2
푘2−1
∞푘
=2
4. 2 푛 ∞푛
=1 5. ln
푛2+1
2푛2+1
∞푛=1 6. (cos 1)푘 ∞푘
=1

Start
Power Series
12/3/2014 57
A power series is a series of the form
푐푛푥푛 ∞푛
=0 = 푐0+푐1푥 +푐2푥2+푐3푥3+푐4푥4+… .
where 푥 is a variable and 푐푛’s are constants called coefficients of the series.
What will happen when 푥 = 1?
A power series may converge for some values of and diverge for other values of . The sum of
the series is a function
푓 푥 = 푐0+푐1푥 +푐2푥2+…+푐푛푥푛 + … .
What will happen when 푐푛 = 1for all n?
The power series becomes the geometric series
푥푛 ∞푛
=0 =1+푥 +푥2+푥3+푥4+… .
which converges when−1 ≤ 푥 ≤ 1 and diverges when 푥 ≥ 1.
More generally, a series of the form
푐푛(푥 − 푎)푛 ∞푛
=0 = 푐0+푐1(푥 − 푎) + 푐2(푥 − 푎)2+…+푐푛(푥 − 푎)푛+… .
is called a power series in 푥 − 푎 or a power series centred at 푎 or a power series about 푎.

Start
Power Series
12/3/2014 58
푐푛(푥 − 푎)푛 ∞푛
=0 = 푐0+푐1(푥 − 푎)+ 푐2(푥 − 푎)2+…+푐푛(푥 − 푎)푛+… .
we have adopted the convention that 푥 − 푎 0 = 1 even when 푥 = 푎. Notice also that
when 푥 = 푎, all of the terms are 0 for 푛 ≥ 1 and so this power series always converges
when 푥 = 푎.
Example 19: For what values of 푥 is the series 푛! 푥푛 ∞푛
=0 convergent?

Start
Power Series
12/3/2014 59
Example 20: For what values of 푥 does this series (푥 − 3)푛/푛 ∞푛
=1 converge?

Start
Power Series
12/3/2014 60
The number 푅 in case (iii) is called the radius of convergence of the power series.

Start
Power Series
12/3/2014 61
REPRESENTATIONS OF FUNCTIONS AS POWER SERIES:
As we can see from the expression of a power series it is a polynomial with infinite number
of terms, so it can be used to represent functions, here we are going to know how this
happens.
From example 16 we know that:
1
1 − 푥
= 1 + 푥 + 푥2 + 푥3 + ⋯ = 푥2
∞
푛=0
푓표푟 푥 < 1 … … … … … (1)
Here we were able to represent the function 1
1−푥 by the power series 푥2 ∞푛
=0 푓표푟 푥
< 1

Start
Power Series
12/3/2014 62
Example 21 : Express 1/(1 − 푥2) as the sum of a power series and find the interval of
convergence.

Start
Power Series
12/3/2014 63
Example 22 : Find a power series representation for 1/(푥 + 2)
Example 23 : Find a power series representation for 푥3/(푥 + 2)

Start
Power Series
12/3/2014 64
REPRESENTATIONS OF FUNCTIONS AS POWER SERIES:

Start
Power Series
12/3/2014 65
Example 24 : Express1 1 − 푥 2 as a power series by differentiation Equation 1. What is
the radius of convergence?

Start
Power Series
12/3/2014 66
Example 25 : Find a power series representation for ln(1 − 푥) and its radius of
convergence?

Start
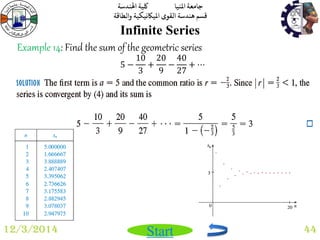
Taylor & Maclaurin Series
12/3/2014 67
Previously we found power series representations for a certain restricted class of functions.
Here we investigate more general problems: Which functions have power series
representations? How can we find such representations?
Let’s start with 푓 which is any function that can be represent with a power series;
푓 푥 = 푐0 + 푐1 푥 − 푎 + 푐2(푥 − 푎)2+푐3(푥 − 푎)3+푐4(푥 − 푎)4+ ⋯ 푥 − 푎 < 푅 (1)
The task here is to find the values of 푐푛 that must be in terms of 푓. To begin, as
mentioned previously when 푥 = 푎 in Equation (1) then 푓(푎) = 푐0.
Differentiating Equation (1) gives
푓′(푥) = 푐1 + 2푐2 푥 − 푎 + 3푐3 푥 − 푎 2 + 4푐4 푥 − 푎 3 + ⋯ 푥 − 푎 < 푅 (2)
and substituting of 푥 = 푎 in Equation (2) gives 푓′(푎) = 푐1
Differentiating Equation (2) gives
푓′′ 푥 = 2푐2 + 2 . 3푐3 푥 − 푎 + 3 . 4푐4 푥 − 푎 2 + ⋯ 푥 − 푎 < 푅 (3)
Again we put x=a in Equation (3). The result is 푓′′ 푎 = 2푐2
Repeating the process we get 푓′′′ 푎 = 3! 푐3
and 푓(푛) 푎 = 2 . 3 . 4 . 5 . … . 푛푐푛 = 푛! 푐푛

Start
12/3/2014 68
Solving this equation for the nth coefficient 푐푛, We get 푐푛 =
푓(푛)(푎)
푛!
THEOREM T&M 1: if 푓 has a power series representation (expansion) at a, that is, if
푓 푥 =
푓 푛 (푎)
푛!
∞
푛=0
(푥 − 푎)푛 푥 − 푎 < 푅
Then its coefficients are given by the formula 푐푛 =
푓(푛)(푎)
푛!
Substituting this formula for back into the series, we see that if has a power series expansion at,
then it must be of the following form.
푓 푥 =
푓 푛 (푎)
푛!
∞
푛=0
(푥 − 푎)푛= 푓 푎 +
푓′ 푎
1!
(푥 − 푎) +
푓′′(푎)
2!
(푥 − 푎)2+
푓′′′(푎)
3!
(푥 − 푎)3+ ⋯
The series is called the Taylor series of the function 푓 at 푎 or about 푎 or centred at 푎 for the
special case 푎=0 the Taylor series becomes Maclaurin series
푓 푥 =
푓 푛 (0)
푛!
∞
푛=0
푥푛 = 푓 0 +
푓′(0)
1!
푥 +
푓′′(0)
2!
푥2 +
푓′′′(0)
3!
푥3 + ⋯

Start
12/3/2014 69
Example 26 : Find the Maclaurin series of the function 푓 푥 = 푒푥 and its radius of
convergence?

Start
12/3/2014 70
From Theorem T&M 1 and example 26 we conclude that if 푒푥 has a power series expansion at 0,
then 푒푥 = 푥푛
푛!
∞푛
=0 .
So how can we determine whether 푒푥 does have a power series representation?
Let’ s investigate the more general question: Under what circumstances is a function equal to
the sum of its Taylor series? In other words, if 푓 has derivatives of all orders, when is it true that
푓 푥 = 푓 푛 (푎)
푛!
∞푛
=0 (푥 − 푎)푛
As with any convergent series, this means that 푓 푥 is the limit of the sequence of partial sums.
In the case of the Taylor series, the partial sums are
푇푛 푥 =
푓 푖 (푎)
푖!
푛
푖=0
(푥 − 푎)푖
= 푓 푎 +
푓′ 푎
1!
푥 − 푎 +
푓′′ 푎
2!
푥 − 푎 2 +
푓′′′ 푎
3!
푥 − 푎 3 + ⋯
+
푓 푛 (푎)
푛!
(푥 − 푎)푛
Notice that 푇푛 is a polynomial of degree 푛 called the nth-degree Taylor polynomial of 푓 at a.

Start
12/3/2014 71
The first the second, and the third sums are
푇1 푥 = 1 + 푥.
푇2 푥 = 1 + 푥 +
푥2
2!
.
푇3 푥 = 1 + 푥 +
푥2
2!
+
푥3
3!
.
In general, f(x) is the sum of its Taylor series if 푓 푥 = lim
푛→∞
푇푛(푥)
If we let 푅푛 푥 = 푓 푥 − 푇푛 푥 so that 푓 푥 = 푇푛 푥 + 푅푛 푥
푅푛 푥 is called the reminder of the Taylor series. If we can somehow show that lim
푛→∞
푅푛 푥 = 0,
then it follows that lim
푛→∞
푇푛 푥 = lim
푛→∞
[푓 푥 − 푅푛 푥 ] = 푓 푥 − lim
푛→∞
푅푛 푥 = 푓(푥)

Start
12/3/2014 72

Start
12/3/2014 73
Example 27: find a. 푒−푥2
푑푥. 푏. 푒−푥2 1
0 푑푥.

Start
12/3/2014 74
Example 28: find lim
푥→0
푒푥−1−푥
푥2

Start
12/3/2014 75
Example 29: find the first three nonzero terms in the Maclaurin series for
a. 푒푥 sin 푥
b. tan 푥

Start
12/3/2014 76
Example 29: find the first three nonzero terms in the Maclaurin series for
a. 푒푥 sin 푥
b. tan 푥

Start
Fourier Series
12/3/2014 77
Fourier series are infinite series that represent periodic functions in terms of cosines and
sines. As such, Fourier series are of greatest importance to the engineer and applied
mathematician. To define Fourier series, we first need some background material. A
function 푓(푥) is called a periodic function if 푓( 푥) is defined for all real 푥, except possibly at
some points, and if there is some positive number p, called a period of 푓( 푥), such that
푓 푥 + 푝 = 푓(푥)
Periodic function of period p

Start
Fourier Series
12/3/2014 78
the fundamental period 푓 푥 + 푛푝 = 푓(푥)
Cosine and sine functions having the period 2

Start
Fourier Series
12/3/2014 79
The series to be obtained will be a trigonometric series, that is, a series of the form
푎0 + 푎1 cos 푥 + 푏1 sin 푥 + 푎2 cos 2푥 + 푏2 sin 2푥 + ⋯ = 푎0 + 푎푛 cos 푛푥 + 푏푛 sin 푛푥
∞
푛→1
.
푎0, 푎1, 푏1, 푎2, 푏2, … are constants, called the coefficients of the series. We see that each term
has the period 2휋Hence if the coefficients are such that the series converges, its sum will be a
function of period 2휋.
푓(푥) = 푎0 + 푎푛 cos 푛푥 + 푏푛 sin 푛푥
∞
푛→1
Is the Fourier Series of 푓(푥) with Fourier Coefficients

Start
Fourier Series
To be continued

Biomedical engineering mathematics i

More Related Content

Featured

Biomedical engineering mathematics i