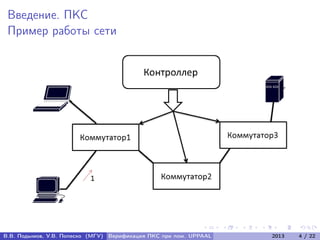
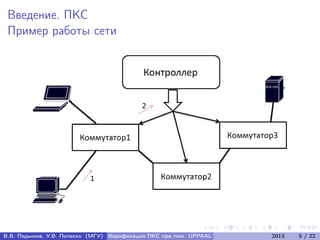
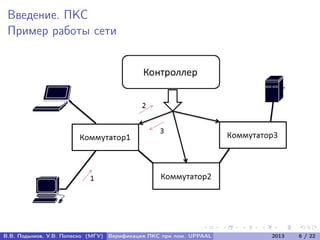
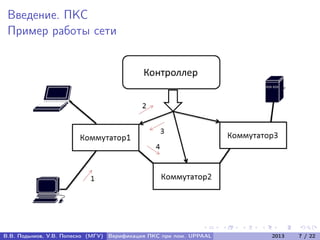
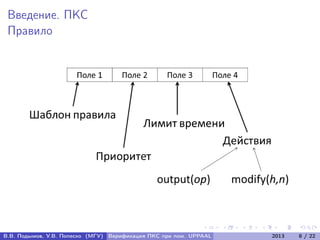
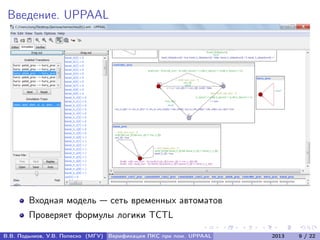
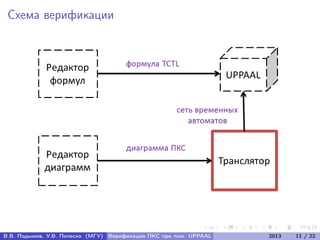
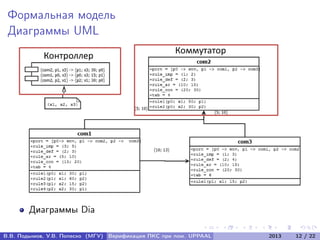
Документ посвящен верификации программно-конфигурируемых сетей (ПКС) с использованием системы UPPAAL. Авторы разрабатывают метод верификации ПКС как распределённых систем реального времени, включая алгоритм трансляции UML-диаграмм в сеть временных автоматов и подтверждение корректности алгоритма. В документе представлены формальные модели, алгоритмы и результаты экспериментальных исследований для анализа поведения ПКС.

1. Верификация программно-конфигурируемых сетей
при помощи системы UPPAAL
В.В. Подымов, У.В. Попеско
МГУ им. М.В. Ломоносова
2013
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 1 / 22

2. План
Введение
Цель
Схема верификации
Формальная модель
Алгоритм трансляции
Корректность алгоритма
Экспериментальное исследование
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 2 / 22

3. Введение. ПКС
Отделение уровня управления от устройств в узлах сети
Программное управление сетью
Стандарт Openflow
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 3 / 22

4. Введение. ПКС
Пример работы сети
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 4 / 22

5. Введение. ПКС
Пример работы сети
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 5 / 22

6. Введение. ПКС
Пример работы сети
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 6 / 22

7. Введение. ПКС
Пример работы сети
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 7 / 22

8. Введение. ПКС
Правило
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 8 / 22

9. Введение. UPPAAL
Входная модель — сеть временных автоматов
Проверяет формулы логики TCTL
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 9 / 22

10. Цель
Разработать метод верификации ПКС
как распределённых систем реального времени
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 10 / 22

11. Схема верификации
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 11 / 22

12. Формальная модель
Диаграммы UML
Диаграммы Dia
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 12 / 22

13. Формальная модель
Формализация всех элементов диаграммы:
коммутатор
контроллер
канал
заголовок пакета
. . .
Формальная семантика сети:
конечное число управляющих состояний элементов диаграммы
(коммутаторов, контроллера, каналов)
локальные таймеры
(бесконечное число значений)
состояние сети:
совокупность управляющих состояний и значений таймеров
сценарии работы сети:
система переписывания
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 13 / 22

14. Формальная модель
Примеры правил переписывания
Применение коммутатором правила r = (p, h, x, p ) ∈ Rule
(t ∈ [L, R]):
Com(select, Rule, t, h, p) → Com(hit, Rule, h, p ),
Отправка коммутатором пакета в канал:
Com(hit, Rule, h, p), Chan(empty) →
Com(start, Rule), Chan(full, 0, h)
Получение коммутатором пакета:
Com(start, Rule), Chan(sent, h) →
Com(select, 0, Rule, h, p), Chan(empty)
Продвижение времени:
все таймеры сдвигаются на одну и ту же величину, если система
не может “прогрессировать”
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 14 / 22

15. Алгоритм трансляции
Вход: UML-диаграмма
Выход: сеть временных автоматов UPPAAL
Принцип работы:
канал −→ переменные + таймер
контроллер −→ временной автомат
коммутатор −→ временной автомат
вспомогательные автоматы
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 15 / 22

16. Алгоритм трансляции
Автомат коммутатора
select
t <= 5 miss
hit
rewrite
t <= 3
start
rule_t[r] >= rule_max[r]
active[r] = false
t >= 3
i = 0..3 -> active[i]
i = 0..3
!active[i]
!c[r]
hurry!
send(c[r], h)
hurry!
send(to_con[0],
(p, h))
i = 1..3 -> active[i]
(i = 0..3)
active[i] && (rule_t[i] > rule_max[i])
active[i] = false
i = 0..3 -> !active[i]
|| (rule_t[i] <= rule_max[i] )
i = 0..3 -> !hit(rule[i])
(i = 0..3)
(t >= 2) && !active[i]
set_rule(i)
from_con[0]
hurry!
get(from_con[0]),
t = 0
rule_t[r] < rule_max[r]
(i = 0..3)
hit(rule[i])
r = i
(i = 1,4,5)
c_ready[i]
hurry!
get(c[i]), p = i, t = 0
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 16 / 22

17. Алгоритм трансляции
Автомат контроллера
send
idle
!con_in[c]
hurry!
send(from_con[c],
rule[r])
i = 0..2 -> !hit(rule[i], (c, p, h))
(i = 0..2)
hit(r[i], (c, p, h))
r = i
(i = 0..2) to_con_ready[i]
hurry! get(to_con[i]), c = i
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 17 / 22

18. Алгоритм трансляции
Вспомогательные автоматы
s1
(i = 0..2 -> ok(to_con[i])) &&
(i = 1..9 -> ok(c[i]))
(i = 1..9)
to_deliver(c[i])
c_ready[i]
(i = 0..2)
to_deliver(to_con[i])
to_con_ready[i])
s1 c[0]
hurry!
c[0] = false
hurry?
s1 (i = 1..3, num = 1..3)
!c[num]
hurry!
send(c[num], i)
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 18 / 22

19. Корректность алгоритма
Теорема (например, Кларк, Грамберг, Пелед. 2002)
Если системы переходов M1, M2 эквивалентны по прореживанию и
формула Φ логики LTL−X истинна для M1, то она также истинна для
M2.
Теорема
Пусть N — произвольная ПКС. Тогда системы переходов TSN и
TSAlg(N) эквивалентны по прореживанию.
Следствие
Алгоритм Alg корректен.
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 19 / 22

20. Корректность алгоритма
Теорема (например, Кларк, Грамберг, Пелед. 2002)
Если системы переходов M1, M2 эквивалентны по прореживанию и
формула Φ логики LTL−X истинна для M1, то она также истинна для
M2.
Теорема
Пусть N — произвольная ПКС. Тогда системы переходов TSN и
TSAlg(N) эквивалентны по прореживанию.
Следствие
Алгоритм Alg корректен.
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 19 / 22

21. Экспериментальное исследование
1 Отсутствие блокировки сети:
A[] not deadlock
2 Постоянное поступление пакетов из внешней среды:
A <> forall(num : int[0, 2]) (channel_h[stream.align[num]])
3 Коммутатор может не принять ни одного пакета:
E[] com1.start
4 Хотя бы один пакет будет обработан контроллером:
E <> !con.idle
5 Хотя бы один пакет успешно перенаправится коммутатором:
E <> com1.hit
Свойство номер:
1 2 3 4 5
2 комм., пустые таблицы 27ч. 1с. 1с. 1с. 1с.
3 комм., кольцо - 1с. 1с. 7с. 1с.
4 комм., звезда - 1с. 1с. 62с. 85с.
4 комм. - 1с. 1с. 60с. 79с.
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 20 / 22

22. Результаты
Предложена формальная модель ПКС как СРВ:
UML-диаграммы
система переписывания
Разработан (и реализован) метод верификации ПКС как СРВ:
алгоритм трансляции UML-диаграмм в сети временных автоматов
корректность алгоритма
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 21 / 22

23. Конец
В.В. Подымов, У.В. Попеско (МГУ) Верификация ПКС при пом. UPPAAL 2013 22 / 22