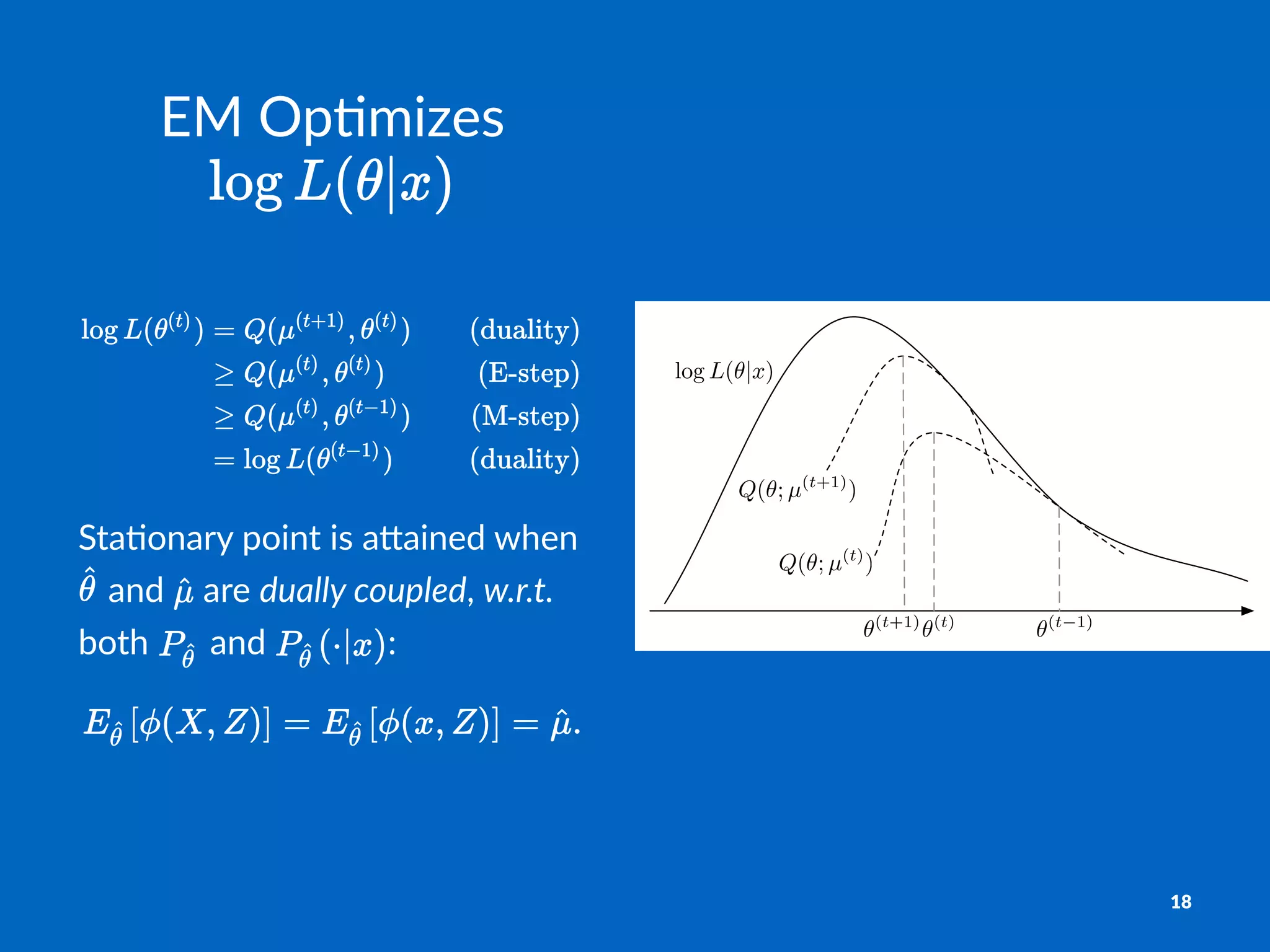
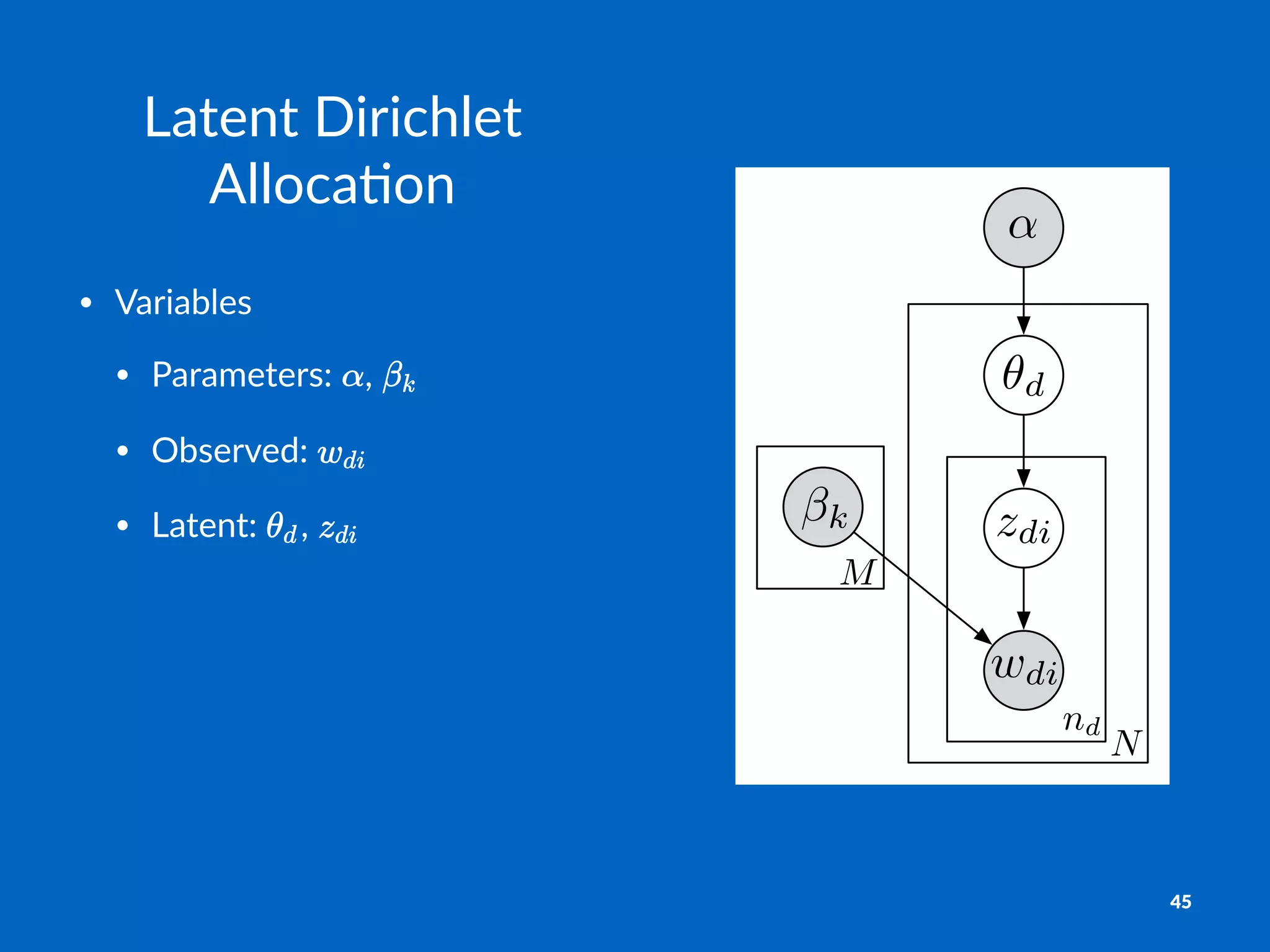
The document discusses variational estimation and inference techniques, focusing on exponential family models, particularly in relation to estimating models with partial observations and using methods like Expectation-Maximization (EM) and variational EM. It covers concepts such as conditional log-partitions, maximizing likelihood through latent variables, and introduces mean field methods to handle intractable expectations. The document outlines various strategies for managing observed and latent variables to optimize estimations effectively.

1. Lecture'5
Varia%onal)Es%ma%on)and)Inference
Dahua%Lin
The$Chinese$University$of$Hong$Kong
1

2. Outline
• Es$ma$on)of)Models)in)Exponen$al)Families
• Es$ma$on)with)par$al)observa$ons)9)EM
• Mean)Field)Methods
2

3. Factorized+Exponen0al+Family
Consider)an)exponen-al)family)of)joint)distribu-ons)
over) :
Here,% %indicates%the%subset%of%components%involved%
in%the% 6th%factor.
3

4. With%Complete%Observa2ons
Given& ,&the&op,mal&es,mates&are&given&by
• With&canonical&parameteriza1on,&this&is&convex.
• Parameters&may&come&with&constraints.
• There&can&be&analy%c'solu%ons,&otherwise,&one&can&
solve&this&using&numerical&methods.&
4

5. Example:)GMM
• GMM"involves:"observed*feature" "and"component*
indicator" .
• How%to%es)mate%if%both% %and% %are%observed?
5

6. Es#mate(GMM
For$ ,$we$maximize
Using&Lagrange&mul.pliers,&we&get
6

7. Es#mate(GMM((cont'd)
For$ ,$we$minimize
where% ,%thus
7

8. Par$ally'Observed'Models
Consider)an)exponen-al)family)involving)observed(
variables) )and)latent(variables) :
Here,% %and% %refer%to%the%observed%parts%and%latent%
parts%of%the%en2re%sample%set.
8

9. Par$ally'Observed'Models'(cont'd)
Given&an&observa,on& ,&we&have
where% %is%called%condi&onal)log+par&&on:
This%also%belongs%to%an%exponen&al)family.
9

10. MLE$with$Par,al$Observa,ons
The$maximum&likelihood&es.mate$is$obtained$by$
maximizing$the$marginal&likelihood$over$observed&data:
10

11. Issues
• The%condi&onal)log+par&&on% %as%below%is%
o-en%very%difficult%to%evaluate:
• We$usually$resort$to$Expecta(on+Maximiza(on0(EM)$
--$a$strategy$that$itera1vely$construct$and$maximize$
lower$bounds$of$ .
11

12. Lower&Bound&of&
Let$ .$
By$conjugate$duality:
with%
!
12

13. Lower&Bound&of& &(cont'd)
Hence,&we&have&
Hence,& &is&a&lower&bound&of& &for&
any& .
13

14. Expecta(on+Maximiza(on
The$Expecta(on+Maximiza(on0(EM)$algorithm$is$
coordinate0ascent$on$ :
• E"step:
• M"step:
14

15. E"step
• Each&E"step&reduces&to&maximize& ,&
the&op4mal&solu4on&is&the&expecta*on&of& :
• By$conjugate*duality,$with$ ,$we$have$
,$thus:
15

16. M"step
• Each&M"step&reduces&to&maximize& ,&
the&op4mal&solu4on&is&a7ained&when
16

17. It#can#be#shown#that#EM#Op&mizes# .#Why?
17

18. log L(✓|x)
Q(✓; µ(t+1)
)
Q(✓; µ(t)
)
✓(t 1)
✓(t)
✓(t+1)
EM#Op&mizes#
Sta$onary)point)is)a-ained)when)
)and) )are)dually&coupled,)w.r.t.)
both) )and) :
18

19. Info.&Geo.&Interpreta-on
• A#parameter# #indicates#a#condi0onal#
distribu0on#over# :# .
• A#mean# #is#realized#by#another#condi0onal#
distribu0on# #with# .
• The#KL#divergence#between#them:
19

20. Info.&Geo.&Interpreta-on
• For%any% %and% :
• E#step:)minimize) )to)close)the)gap)
between) )and) .
• M#step:)M#projec;on)of) )onto) .
20

21. EM#with#iid#samples
Consider)a)common)problem:) )
are)generated)from)an)exponen5al)family)distribu5on,)
and)only) )is)observed)for)each) :
!
21

22. EM#with#iid#samples#(cont'd)
Lower&bound& &is:
It#has:
22

23. • E#step:)
• M#step:)
op#ma&a'ained&when
23

24. EM#for#GMM
• The%condi&onal)expecta&on%is%determined%by%
.
• E1step%computes:
24

25. EM#for#GMM#(cont'd)
Given& ,&M)step:
25

26. What%if%it%is%intractable%to%compute%the%expected%
sufficient%sta6s6cs% ?
26

27. Varia%onal)EM
• Basic&idea:"Use"a"distribu-on" "from"a"tractable"
family" "to"approximate" ,"and"thus"
"to"approximate" .
• This"is"to"restrict" "to"
.
• The"lower"bound"becomes:
27

28. Varia%onal)EM)(cont'd)
• Varia%onal)E+step:"with"restric+on"to" ,"
compu+ng" "is"tractable:
!
• M"step:"remains"the"same
28

29. Varia%onal)E+step
• "is"usually"chosen"to"be"an"exponen&al)family,"
parameterized"by" ."Then"the"varia&onal)E1step"
reduces"into"two"steps.
• Step"1:"Find"op=mal" "through"I1projec&on:
• Step&2:&Compute&
29

30. Key$Problem
• With& &given,& &remains&an&exponen3al&
family&distribu3on:&
&with&
&and& .
• &plays&a&key&role&in&model&es3ma3on.
• Key$problem:&choose&a&tractable&distribu3on& &
from& &to&approximate& &and&compute&
30

31. Mean%Field%Methods
• Consider*an*exponen.al*family*distribu.on* *for*
which*it*is*intractable*to*compute*the*mean*given* .
• Mean%field%methods*use*a*distribu.on* *from*a*
tractable*family,*usually*in*a*product%form,*to*
approximate*the*given*distribu.on* ,*and*use*
*to*approximate* .*
31

32. Product(Form
• We$say$a$joint$distribu1on$over$ $
is$of$the$product(form,$if$its$density$can$be$wri8en:
• An$exponen&al)family$of$product)form:
32

33. Product(Form((cont'd)
• Log%par))on+func)on:
• Expecta)on:
• If$each$factor$is$tractable,$then$the$whole$
distribu5on$is$tractable.
33

34. Ising&Model&(formula2on)
It#is#intractable#to#compute# #exactly.
34

35. Ising&Model&(factorized&model)
Consider)a)factorized)model
where% .%Then
35

36. Ising&Model&(approxima2on)
To#find# #that#approximates# ,#we#perform#I"
projec)on#of# #onto#the#factorized1family# :
with% .
36

37. Ising&Model&(approxima2on)
The$best$approxima(on$can$be$solved$itera1vely:
Whereas' 'is'in'a'product(form,'the'parameters'
associated'with'different'components'are'usually'
coupled'in'the'op6mal'approxima6on.
37

38. Mean%Field%Theory
Consider)an)exponen&al)family:)
and$a$tractable(family$ .$Then$for$any$ :
!
!can!generally!be!factorized!into!simpler!forms.
38

39. Mean%Field%Theory%(cont'd)
The$difference$between$ $and$the$tractable(lower(
bound$is$the$KL$divergence:
with% .%The%op+ma% %is%the%I"projec)on:
39

40. Naive&Mean&Field
The$mean%field%methods$are$called$naive%mean%field$
when$ $is$of$product%form.$Consider:
and
40

41. Hence,&the&nega+ve&entropy&of& &can&be&factorized:
The$op'ma$ $can$be$solved$by$minimizing:
where% .
41

42. Naive&Mean&Field&(Op/ma)
• This&problem&can&be&solved&by&coordinate*descent.&
• When&op6ma&is&a7ained:&
• Hence,'the'op,ma' 'is'given'by'
42

43. Naive&Mean&Field&(Discussion)
• In$naive$mean$field,$while$ $is$of$a$product$form,$
the$parameters$associated$with$different$
components$are$generally$coupled$in$the$op;mal$
approxima;on.
• The$I"projec)on$problem$in$naive$mean$field$is$non#
convex$in$general.$In$prac;ce,$the$coordinate$
ascent$procedure$can$be$trapped$in$a$local-valley.$
• Generally,$it$is$unclear$how$far$ $is$from$ .
43

44. Varia%onal)EM)(Recap)
• E#step((for(each(sample( ):
• M#step:
44

45. M
N
nd
↵
✓d
zdi
wdi
k
Latent&Dirichlet&
Alloca/on
• Variables
• Parameters:. ,.
• Observed:.
• Latent:. ,.
45

46. Condi&onal)Distribu&on
Let$ $and$ :
Two$latent&suff.stats.:$ $and$ .$
46

47. Varia%onal)Distribu%on
• :#Dirichlet#with#
• :#Categorical#with# .
47

48. Varia%onal)E+Steps
• For% :
• For% :
48

49. M"Step
49