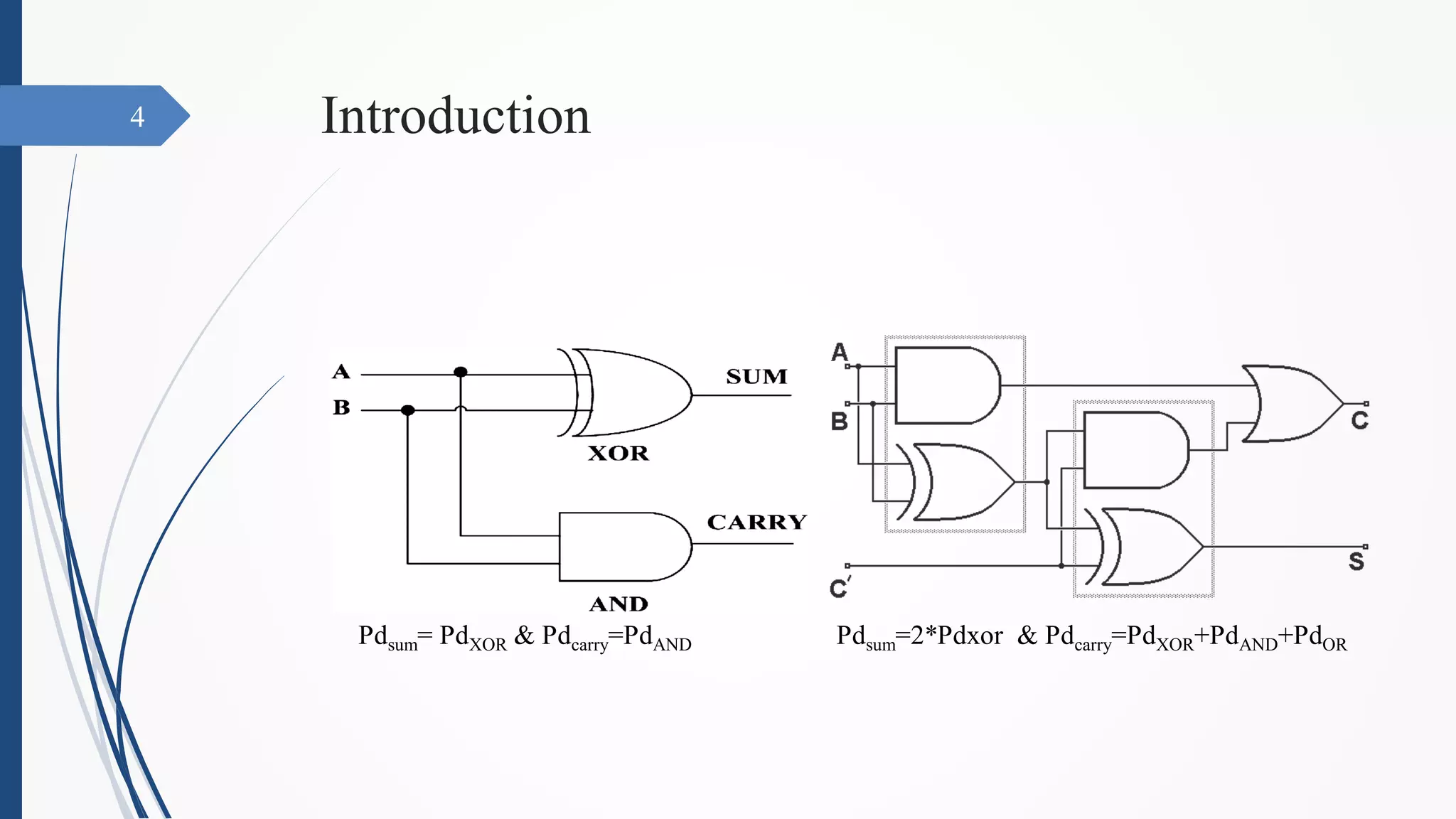
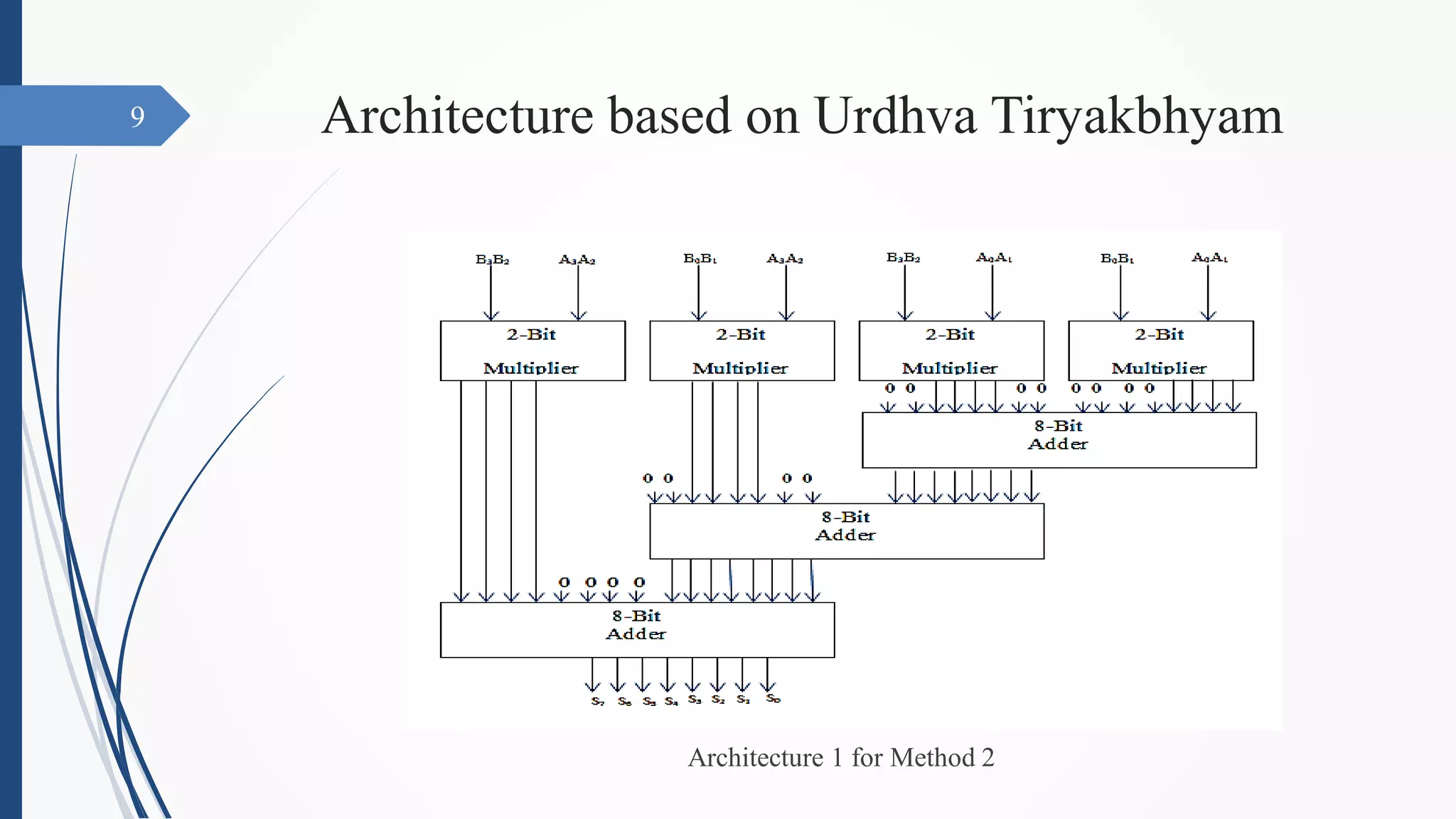
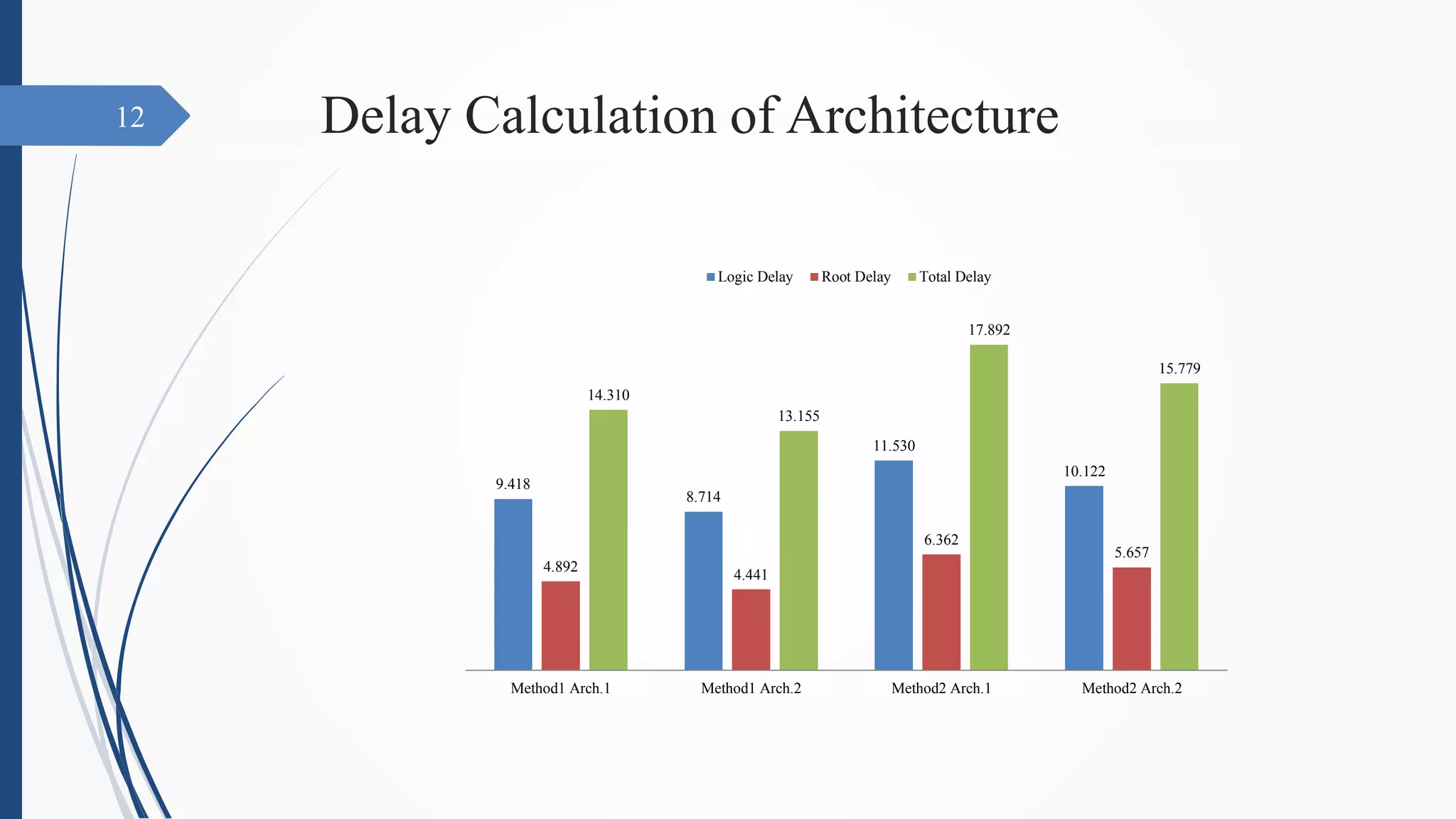
This document presents VHDL code for a Vedic multiplier with minimum delay architecture. It introduces the Vedic multiplication method of Urdhva-tiryakbhyam, which means vertically and crosswise. Two architectures are presented based on this method, with the second architecture aimed at reducing hardware. Delay calculations are shown for both architectures, with Architecture 1 of Method 1 having the lowest delay. In conclusion, the architecture of Method 1 with reduced hardware is found to have the lowest delay.

1. VHDL Code of Vedic Multiplier
with Minimum Delay Architecture
Presented By
Vaibhav Jindal
Gautam Buddha University
1

2. Contents
 Introduction
 Vedic Method 1 (Urdhva Tiryakbhyam)
 Architecture based on Urdhva Tiryakbhyam
 Vedic Method 2 (Urdhva Tiryakbhyam)
 Architecture based on Urdhva Tiryakbhyam
 Delay Calculation of Architecture
 Conclusion
 References
2

3. Introduction
 Vedic mathematics is the name given to the ancient system of mathematics, which was
rediscovered, from the Vedas between 1911 and 1918 by Sri Bharati Krishna Tirthaji.
 The Vedic multiplication has 16 sutras.
 Urdhva-tiryakbhyam -Vertically and crosswise.
3

4. Introduction
Pdsum= PdXOR & Pdcarry=PdAND Pdsum=2*Pdxor & Pdcarry=PdXOR+PdAND+PdOR
4

5. Vedic Method 1 (Urdhva Tiryakbhyam)
Method -1 of 4-bit Vedic Multiplier
5

6. Architecture based on Urdhva Tiryakbhyam
Architecture 1 for Method1
6

7. Architecture(Hardware Reduce) based on Urdhva
Tiryakbhyam
Architecture 2 for Method1
7

8. Vedic Method 2 (Urdhva Tiryakbhyam)
Method -2 of 4-bit Vedic Multiplier
8

9. Architecture based on Urdhva Tiryakbhyam
Architecture 1 for Method 2
9

10. Architecture(Hardware Reduce) based on Urdhva
Tiryakbhyam
Architecture 2 for Method 2
10

11. Delay Calculation of Architectures
Delay Manually
calculated
Slice
Occupied
Total
Delay
(ns)
Method1
Arch.1
PdAND+11xPdHA
+5xPdOR
20 14.310
Method1
Arch.2
PdAND+10xPdHA
+4xPdOR
19 13.155
Method2
Arch.1
PdAND+47xPdHA
+15xPdOR
20 17.829
Method2
Arch.2
PdAND+23xPdHA
+6xPdOR
19 15.779
11
Delay calculation on Xilinx (Spartan 3E) Device XC3S500E

12. Delay Calculation of Architecture
9.418
8.714
11.530
10.122
4.892
4.441
6.362
5.657
14.310
13.155
17.892
15.779
Method1 Arch.1 Method1 Arch.2 Method2 Arch.1 Method2 Arch.2
Logic Delay Root Delay Total Delay
12

13. Conclusion
 The architecture of metho1 with reduce hardware has the less delay
than others architecture.
 So, it will enhancing the ability of process or the time of process
will be as low as possible.
13

14. References
 Kabiraj Sethi and Rutuparna Panda, “An Improvedsquaring Circuit For Binary Numbers”,
International Journal of Advanced Computer Science and Applications, Vol. 3, 2012.
 Purushottam D. Chidgupkar and Mangesh T. Karad, “The Implementation of Vedic Algorithms in
Digital Signal Processing”, 7th UICEE Annual Conference on Engineering Education,Global J.
of Engng. Educ., Vol.8, 2012.
 PoornimaM,shivraj Kumar Patil, Shivkumar, Shridhar K P and Sanjay H, “Implementation of
Multiplier using Vedic Algorithm”, International Journal of Innovative Technology and
Exploring Engineering, Vol.2, 2013.
 Premananda B.S., Samarth S. Pai, Shashank B.,Shashank S. Bhat, “Design and Implementation
of 8-Bit Vedic Multiplier”, International Journal of Advanced Research in Electrical, Electronic
and Instrumentation Engineering, Vol.2, 2013.
 R.Shridevi, Anirudh Palakurthi, Akhila Sadhula, Hafsa Mahreen, “Design of a High Speed
Multiplier (Ancient Vedic Mathematics Approach) ” International Journal of Engineering
Research, Vol.2, 2013.
14

15. Thanks’
Questions ?
15