Searching techniques involve finding a value with specified properties within a collection. Linear searching compares each item sequentially until a match is found, taking O(n) time. Binary searching requires a sorted list and compares the middle item first, reducing the search space by half with each comparison, taking O(log n) time on average. Sorting rearranges elements in ascending or descending order using techniques like bubble, insertion, and selection sort that have O(n^2) worst-case time and quicksort that has an average case of O(n log n) time.

1. Searching techniques
Searching :
It is a process to find whether a particular value with specified properties is present or not
among a collection of items.
If the value is present in the collection, then searching is said to be successful, and it
returns the location of the value in the array.
Otherwise, if the value is not present in the array, the searching process displays the
appropriate message and in this case searching is said to be unsuccessful.
1) Linear or Sequential Searching 2) Binary Searching
int main( ) { Linear_Search (A[ ], N, val , pos )
int arr [ 50 ] , num , i , n , pos = -1; Step 1 : Set pos = -1 and k = 0
printf ("How many elements to sort : "); Step 2 : Repeat while k < N
scanf ("%d", &n); Begin
printf ("n Enter the elements : nn"); Step 3 : if A[ k ] = val
for( i = 0; i < n; i++ ) { Set pos = k
printf (“arr [%d ] : “ , i ); print pos
scanf( "%d", &arr[ i ] ); Goto step 5
} End while
printf(“nEnter the number to be searched : “); Step 4 : print “Value is not present”
scanf(“%d”,&num); Step 5 : Exit
for(i=0;i<n;i++)
if( arr [ i ] == num ) { Searches
pos = i ; break; -- for each item one by one in the list from
} the first, until the match is found.
if ( pos == -1 ) printf(“ %d does not exist ”,num); Efficiency of Linear search :
else -- Executes in O ( n ) times where n is the
printf(“ %d is found at location : %d”, num , pos); number of elements in the list.

2. Binary Searching
Algorithm:
• Before searching, the list of items should be sorted in ascending order.
• We first compare the key value with the item in the position of the array. If there is a match, we
can return immediately the position.
• if the value is less than the element in middle location of the array, the required value is lie in
the lower half of the array.
• if the value is greater than the element in middle location of the array, the required value is lie
in the upper half of the array.
• We repeat the above procedure on the lower half or upper half of the array.
Binary_Search (A [ ], U_bound, VAL)
Step 1 : set BEG = 0 , END = U_bound , POS = -1
Step 2 : Repeat while (BEG <= END ) void binary_serch ( int a [], int n, int val ) {
Step 3 : set MID = ( BEG + END ) / 2 int end = n - 1, beg = 0, pos = -1;
Step 4 : if A [ MID ] == VAL then while( beg <= end ) {
POS = MID mid = ( beg + end ) / 2;
print VAL “ is available at “, POS if ( val == a [ mid ] ) {
GoTo Step 6 pos = mid;
End if printf(“%d is available at %d”,val, pos );
if A [ MID ] > VAL then break;
set END = MID – 1 }
Else if ( a [ mid ] > val ) end = mid – 1;
set BEG = MID + 1 else beg = mid + 1;
End if }
End while if ( pos = - 1)
Step 5 : if POS = -1 then printf( “%d does not exist “, val );
print VAL “ is not present “ }
End if
Step 6 : EXIT

3. Sorting
Sorting is a technique to rearrange the elements of a list in ascending or
descending order, which can be numerical, lexicographical, or any user-defined order.
Ranking of students is the process of sorting in descending order.
EMCET Ranking is an example for sorting with user-defined order.
EMCET Ranking is done with the following priorities.
i) First priority is marks obtained in EMCET.
ii) If marks are same, the ranking will be done with comparing marks obtained in
the Mathematics subject.
iii) If marks in Mathematics subject are also same, then the date of births will be
compared.
Internal Sorting : Types of Internal Sortings
If all the data that is to be sorted can be accommodated
at a time in memory is called internal sorting.  Bubble Sort
External Sorting :
 Insertion Sort
It is applied to Huge amount of data that cannot be  Selection Sort
accommodated in memory all at a time. So data in disk
or file is loaded into memory part by part. Each part that  Quick Sort
is loaded is sorted separately, and stored in an
intermediate file and all parts are merged into one single  Merge Sort
sorted list.

4. Bubble Sort
Bubbles up the highest
Unsorted Sorted
Bubble_Sort ( A [ ] , N )
Step 1 : Repeat For P = 1 to N – 1
10 54 54 54 54 54 Begin
Step 2 : Repeat For J = 1 to N – P
47 10 47 47 47 47 Begin
Step 3 : If ( A [ J ] < A [ J – 1 ] )
12 47 10 23 23 23 Swap ( A [ J ] , A [ J – 1 ] )
End For
54 12 23 10 19 19 End For
Step 4 : Exit
19 23 12 19 10 12
Complexity of Bubble_Sort
23 19 19 12 12 10 The complexity of sorting algorithm is
depends upon the number of comparisons
Original After After After After After that are made.
List Pass 1 Pass 2 Pass 3 Pass 4 Pass 5 Total comparisons in Bubble sort is
n ( n – 1) / 2 ≈ n 2 – n
Complexity = O ( n 2 )

5. void print_array (int a[ ], int n) {
int i;
for (i=0;I < n ; i++) printf("%5d",a[ i ]);
Bubble Sort
}
void bubble_sort ( int arr [ ], int n) {
int pass, current, temp;
For pass = 1 to N - 1
for ( pass=1;(pass < n) ;pass++) {
for ( current=1;current <= n – pass ; current++) {
if ( arr[ current - 1 ] > arr[ current ] ) {
temp = arr[ current - 1 ]; For J = 1 to N - pass
arr[ current - 1 ] = arr[ current ];
arr[ current ] = temp;
} T
A[J–1]>A[J]
}
}
} F
int main() { Temp = A [ J – 1 ]
int count,num[50],i ; A[J–1]=A[J]
printf ("How many elements to be sorted : "); A [ J ] = Temp
scanf ("%d", &count);
printf("n Enter the elements : nn");
for ( i = 0; i < count; i++) {
printf ("num [%d] : ", i ); scanf( "%d", &num[ i ] );
}
printf("n Array Before Sorting : nnn");
print_array ( num, count );
Return
bubble_sort ( num, count);
printf("nnn Array After Sorting : nnn");
print_array ( num, count );
}

6. TEMP Insertion Sort
Insertion_Sort ( A [ ] , N )
78 23 45 8 32 36 Step 1 : Repeat For K = 1 to N – 1
23 Begin
Step 2 : Set Temp = A [ K ]
Step 3 : Set J = K – 1
23 78 45 8 32 36 Step 4 : Repeat while Temp < A [ J ] AND J >= 0
45 Begin
Set A [ J + 1 ] = A [ J ]
Set J = J - 1
23 45 78 8 32 36 End While
Step 5 : Set A [ J + 1 ] = Temp
8
End For
Step 4 : Exit
8 23 45 78 32 36
32 insertion_sort ( int A[ ] , int n ) {
int k , j , temp ;
8 23 32 45 78 36 for ( k = 1 ; k < n ; k++ ) {
temp = A [ k ] ;
36 j = k - 1;
while ( ( temp < A [ j ] ) && ( j >= 0 ) ) {
8 23 32 36 45 78 A[j+1] =A[j];
j--;
Complexity of Insertion Sort }
Best Case : O ( n ) A [ j + 1 ] = temp ;
Average Case : O ( n2 ) }
Worst Case : O ( n2 ) }

7. Smallest Selection Sort ( Select the smallest and Exchange )
Selection_Sort ( A [ ] , N )
8 23 78 45 8 32 56 Step 1 : Repeat For K = 0 to N – 2
Begin
Step 2 : Set POS = K
Step 3 : Repeat for J = K + 1 to N – 1
23 8 78 45 23 32 56 Begin
If A[ J ] < A [ POS ]
Set POS = J
32 8 23 45 78 32 56 End For
Step 5 : Swap A [ K ] with A [ POS ]
End For
Step 6 : Exit
45 8 23 32 78 45 56
selection_sort ( int A[ ] , int n ) {
int k , j , pos , temp ;
for ( k = 0 ; k < n - 1 ; k++ ) {
56 8 23 32 45 78 56 pos = k ;
for ( j = k + 1 ; j <= n ; j ++ ) {
if ( A [ j ] < A [ pos ] )
8 23 32 45 56 78 pos = j ;
}
temp = A [ k ] ;
Complexity of Selection Sort A [ k ] = A [ pos ] ;
Best Case : O ( n2 )
A [ pos ] = temp ;
Average Case : O ( n2 ) }
Worst Case : O ( n2 ) }

8. Selection sort
Insertion sort
k = 0; k < n - 1 ; k++
k = 1; k < n ; k++
pos = k
temp = a [ k ]
j=k-1
j = k + 1 ; j < n ; j++
temp < a [ j ] && j >= 0
a[ j ] < a[ pos ]
a[j+1]=a[j] pos = j
j=j-1
a [ j + 1 ] = temp temp = a[ k ]
a [ k ] = a [ pos ]
a [ pos ] = temp
return
return

9. Bubble sort – Insertion sort – Selection sort
Bubble Sort :
-- very primitive algorithm like linear search, and least efficient .
-- No of swappings are more compare with other sorting techniques.
-- It is not capable of minimizing the travel through the array like insertion sort.
Insertion Sort :
-- sorted by considering one item at a time.
-- efficient to use on small sets of data.
-- twice as fast as the bubble sort.
-- 40% faster than the selection sort.
-- no swapping is required.
-- It is said to be online sorting because it continues the sorting a list as and when it receives
new elements.
-- it does not change the relative order of elements with equal keys.
-- reduces unnecessary travel through the array.
-- requires low and constant amount of extra memory space.
-- less efficient for larger lists.
Selection sort :
-- No of swappings will be minimized. i.e., one swap on one pass.
-- generally used for sorting files with large objects and small keys.
-- It is 60% more efficient than bubble sort and 40% less efficient than insertion sort.
-- It is preferred over bubble sort for jumbled array as it requires less items to be exchanged.
-- uses internal sorting that requires more memory space.
-- It cannot recognize sorted list and carryout the sorting from the beginning, when new elements
are added to the list.

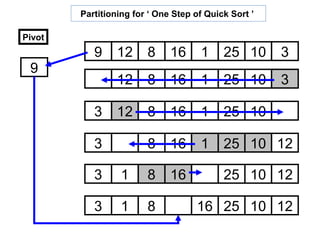
10. Quick Sort – A recursive process of sorting
Original-list of 11 elements :
8 3 2 11 5 14 0 2 9 4 20 Algorithm for Quick_Sort :
Set list [ 0 ] as pivot : -- set the element A [ start_index ] as pivot.
-- rearrange the array so that :
pivot
-- all elements which are less than the pivot
come left ( before ) to the pivot.
8 3 2 11 5 14 0 2 9 4 20 -- all elements which are greater than the pivot
come right ( after ) to the pivot.
Rearrange ( partition ) the elements -- recursively apply quick-sort on the sub-list of
into two sub lists : lesser elements.
pivot -- recursively apply quick-sort on the sub-list of
greater elements.
4 3 2 2 5 0 8 11 9 14 20 -- the base case of the recursion is lists of size
zero or one, which are always sorted.
Sub-list of Sub-list of
lesser elements greater elements
Complexity of Quick Sort
Best Case : O ( n log n )
Apply Quick-sort Apply Quick-sort Average Case : O ( n log n )
recursively recursively Worst Case : O ( n2 )
on sub-list on sub-list

11. Partitioning for ‘ One Step of Quick Sort ’
Pivot
9 12 8 16 1 25 10 3
9
12 8 16 1 25 10 3
3 12 8 16 1 25 10
3 8 16 1 25 10 12
3 1 8 16 25 10 12
3 1 8 16 25 10 12

12. Quick Sort – Program
int partition ( int a [ ], int beg, int end ) { void quick_sort(int a[ ] , int beg , int end ) {
int left , right , loc , flag = 0, pivot ; int loc;
loc = left = beg; if ( beg < end ) {
right = end; loc = partition( a , beg , end );
pivot = a [ loc ] ; quick_sort ( a , beg , loc – 1 );
while ( flag == 0 ) quick_sort ( a , loc + 1 , end );
{ }
while( (pivot <= a [ right ] )&&( loc != right ) ) }
right - - ; void print_array (int a [ ],int n) {
if( loc == right ) flag = 1; int i;
else { for ( i = 0 ; I < n ; i++ ) printf( "%5d“ ,a [ i ] ) ;
a [ loc ] = a [ right ] ; }
left = loc + 1 ; int main () {
loc = right; int count , num[ 50 ] , i ;
} printf ("How many elements to sort : ");
while ( (pivot >= a [ left ] ) && ( loc != left ) ) scanf ("%d", &count );
left++; printf ("n Enter the elements : nn");
if( loc == left ) flag = 1; for( i = 0; i < count; i++ ) {
else { printf ("num [%d ] : “ , i );
a [ loc ] = a [ left ] ; scanf( "%d", &num[ i ] );
right = loc - 1; }
loc = left; printf (“ n Array Before Sorting : nnn“ );
} print_array ( num , count ) ;
} quick_sort ( num ,0 , count-1) ;
a [ loc ] = pivot; printf ( "nnn Array After Sorting : nnn“ );
return loc; print_array ( num , count );
} }

13. partition ( int a [ ], int beg, int end ) A B
loc = left = beg F T
loc == left
flag = 0, right = end
pivot = a [ loc ]
a [ loc ] = a [ left ] flag = 1
Flag == 0 right = loc - 1 ;
loc = left;
pivot <= a [ right ]
&& loc != right
a[ loc ] = pivot
right = right - 1
return loc
F T
loc == right quick_sort ( int a [ ], int beg, int end )
a [ loc ] = a [ right ] flag = 1 F T
left = loc + 1 ; loc == left
loc = right;
loc = partition( a , beg , end )
pivot >= a [ left ]
&&loc != left quick_sort ( a , beg , end )
left = left + 1 quick_sort ( a , beg , end )
return
A B

14. Merge Sort ( Divide and conquer )
Divide the array
-- Merge sort technique sorts a given set
39 9 81 45 90 27 72 18 of values by combining two sorted
arrays into one larger sorted arrays.
-- A small list will take fewer steps to sort
39 9 81 45 90 27 72 18 than a large list.
-- Fewer steps are required to construct
a sorted list from two sorted lists than
39 9 81 45 90 27 72 18
two unsorted lists.
-- You only have to traverse each list
39 9 81 45 90 27 72 18 once if they're already sorted .
Merge the elements to sorted array Merge_sort Algorithm
1. If the list is of length 0 or 1, then it is already
sorted.
39 9 81 45 90 27 72 18 Otherwise:
2. Divide the unsorted list into two sublists of
about half the size.
9 39 45 81 27 90 18 72 3. Sort each sublist recursively by re-applying
merge sort.
4. Merge the two sublists back into one
9 39 45 81 18 27 72 90 sorted list.
Time complexity
9 18 27 39 45 72 81 90 Worst case - O(n log n)
Best case - O(nlogn) typical, O(n) natural variant
Average case - O( n log n )

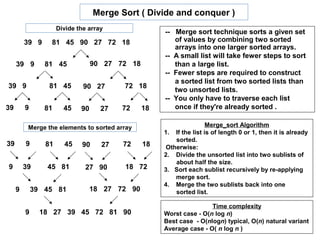
15. Merge Sort - Program
void merge(int a[ ],int low,int high,int mid){
int i, j, k, c[50];
i=low; j=mid+1; k=low;
while( ( i<=mid )&&( j <= high ) ) { void print_array (int a [ ],int n) {
int i;
if( a[ i ]<a[ j ] ){ for ( i = 0 ; I < n ; i++ ) printf( "%5d“ ,a [ i ] ) ;
c[ k ]=a[ i ]; k++; i++; }
}else { int main () {
c[ k ]=a[ j ]; k++; j++; int count , num[ 50 ] , i ;
} printf ("How many elements to sort : ");
} scanf ("%d", &count );
while( i<=mid ) { c[k]=a[ i ]; k++; i++; } printf ("n Enter the elements : nn");
for( i = 0; i < count; i++ ) {
while(j<=high) { c[k]=a[ j ]; k++; j++; } printf ("num [%d ] : “ , i );
for(i=low;i<k;i++) a[ i ]=c[ i ]; scanf( "%d", &num[ i ] );
} }
printf (“ n Array Before Sorting : nnn“ );
void merge_sort(int a[ ], int low, int high){
print_array ( num , count ) ;
int mid;
merge_sort ( num ,0 , count-1) ;
if( low < high) {
printf ( "nnn Array After Sorting : nnn“ );
mid=(low+high)/2; print_array ( num , count );
merge_sort (a, low, mid); }
merge_sort (a, mid+1 ,high);
merge (a, low, high, mid);
}
}

16. merge
i =low ; j = mid+1;k = low
Merge_Sort
i <= mid && j <= high
T F T
F low < high
a[ i ] < a[ j ]
c[ k ] =a [ i ] ; c[ k ] =a [ j ] ; mid = ( low + high ) / 2
k++ ; i++ k++ ; j++
merge_sort (a, low, mid)
i <= mid
merge_sort (a, mid, high )
c[ k ] =a [ i ] ; k++ ; i++
Merge (a, low,high , mid)
j <= high
c[ k ] =a [ j ] ; k++ ; j++
i = low ; i < k ; i ++
Return
a[ i ] = c [ i ]
return

17. www.jntuworld.com
• For More Materials, Text Books, Previous
Papers & Mobile updates of B.TECH,
B.PHARMACY, MBA, MCA of JNTU-HYD,JNTU-
KAKINADA & JNTU-ANANTAPUR visit
www.jntuworld.com