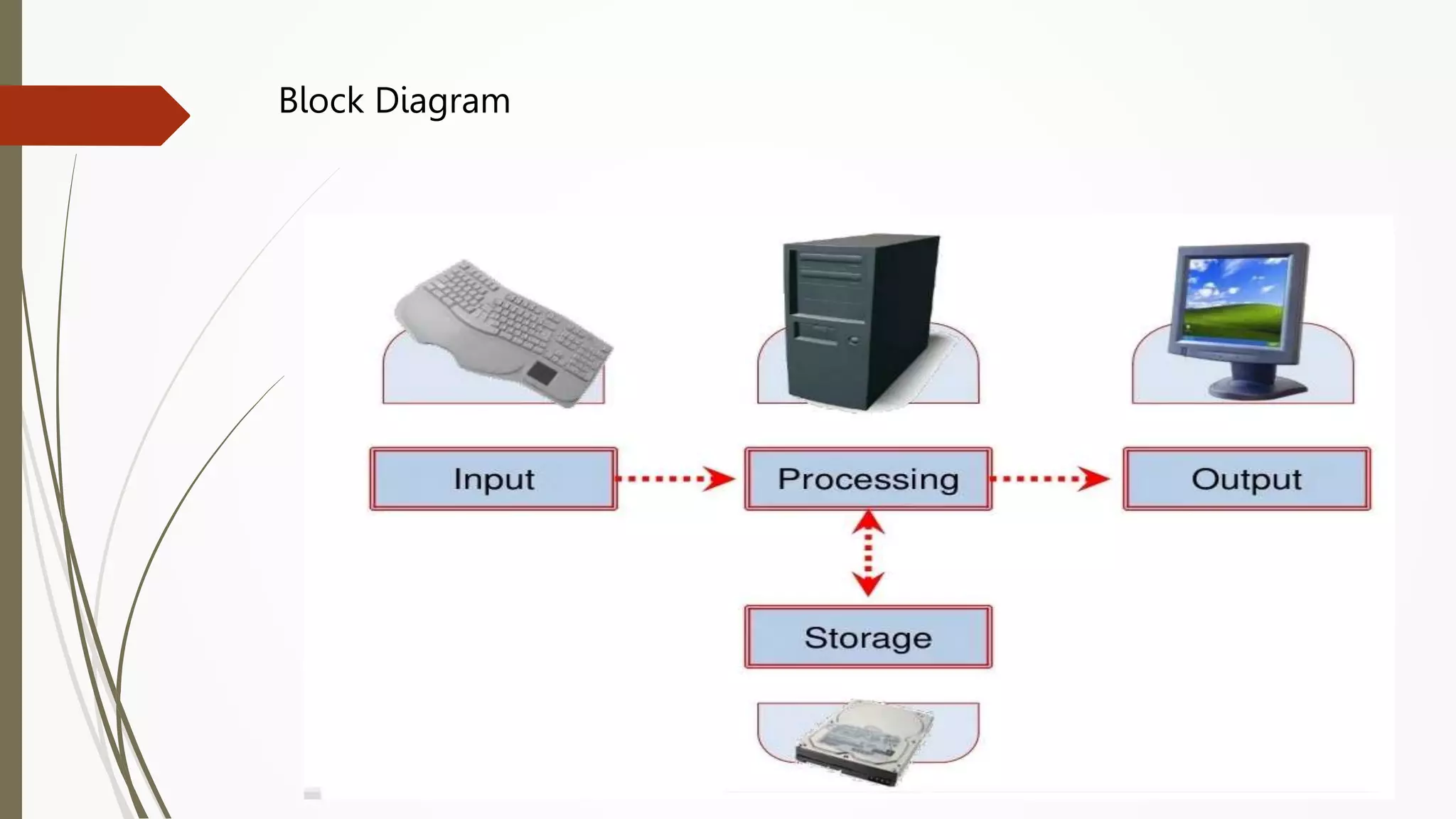
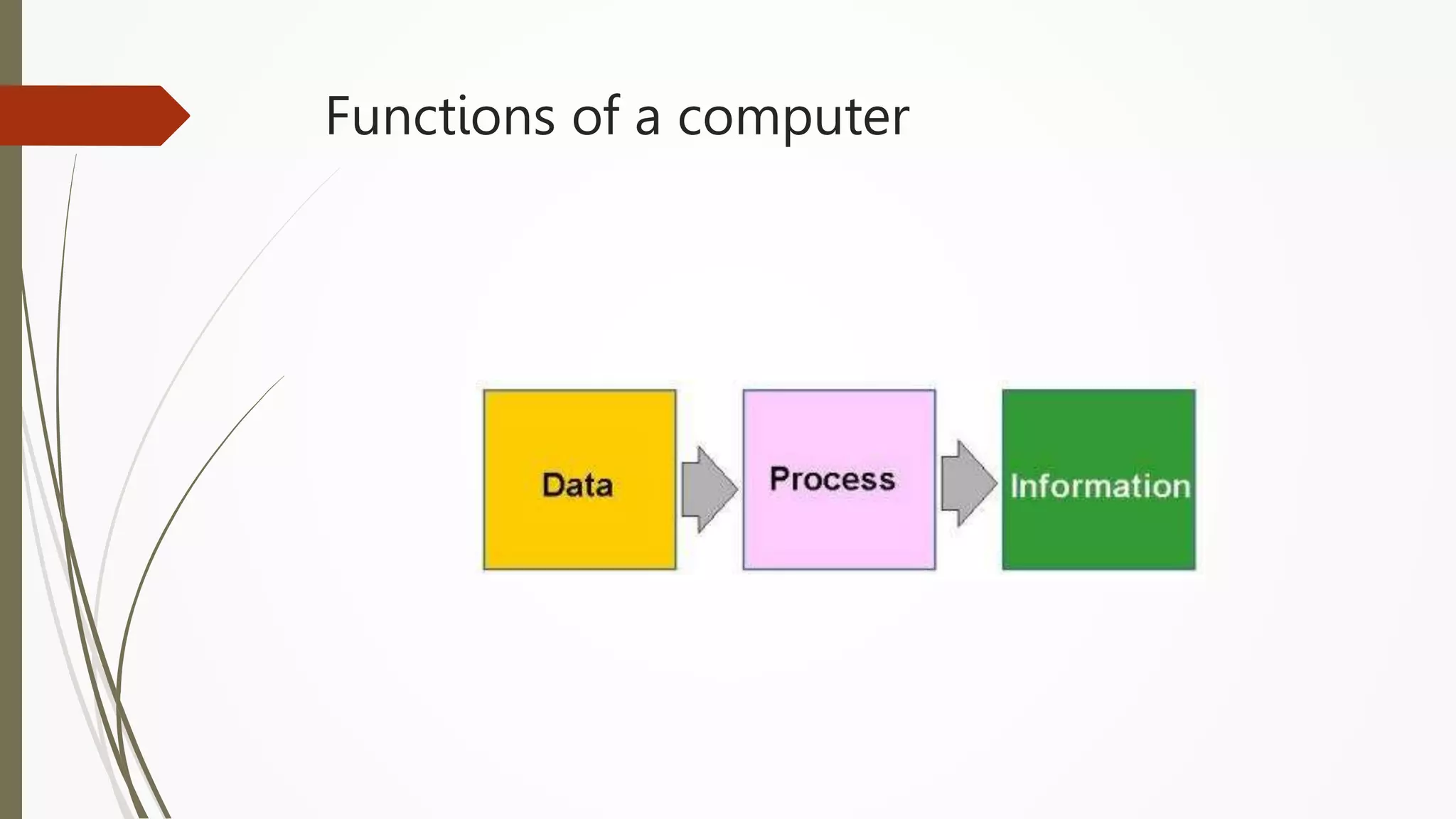
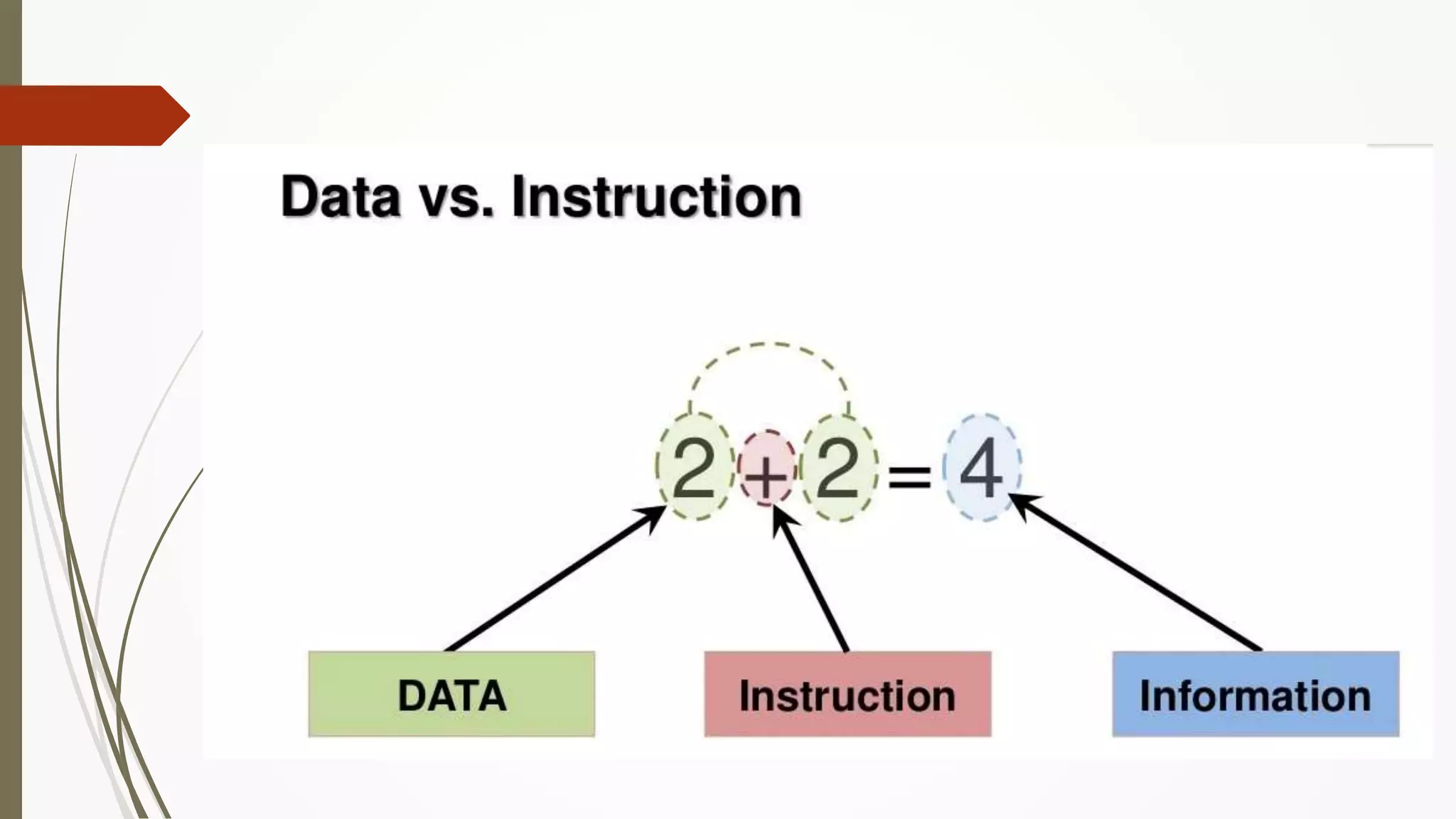
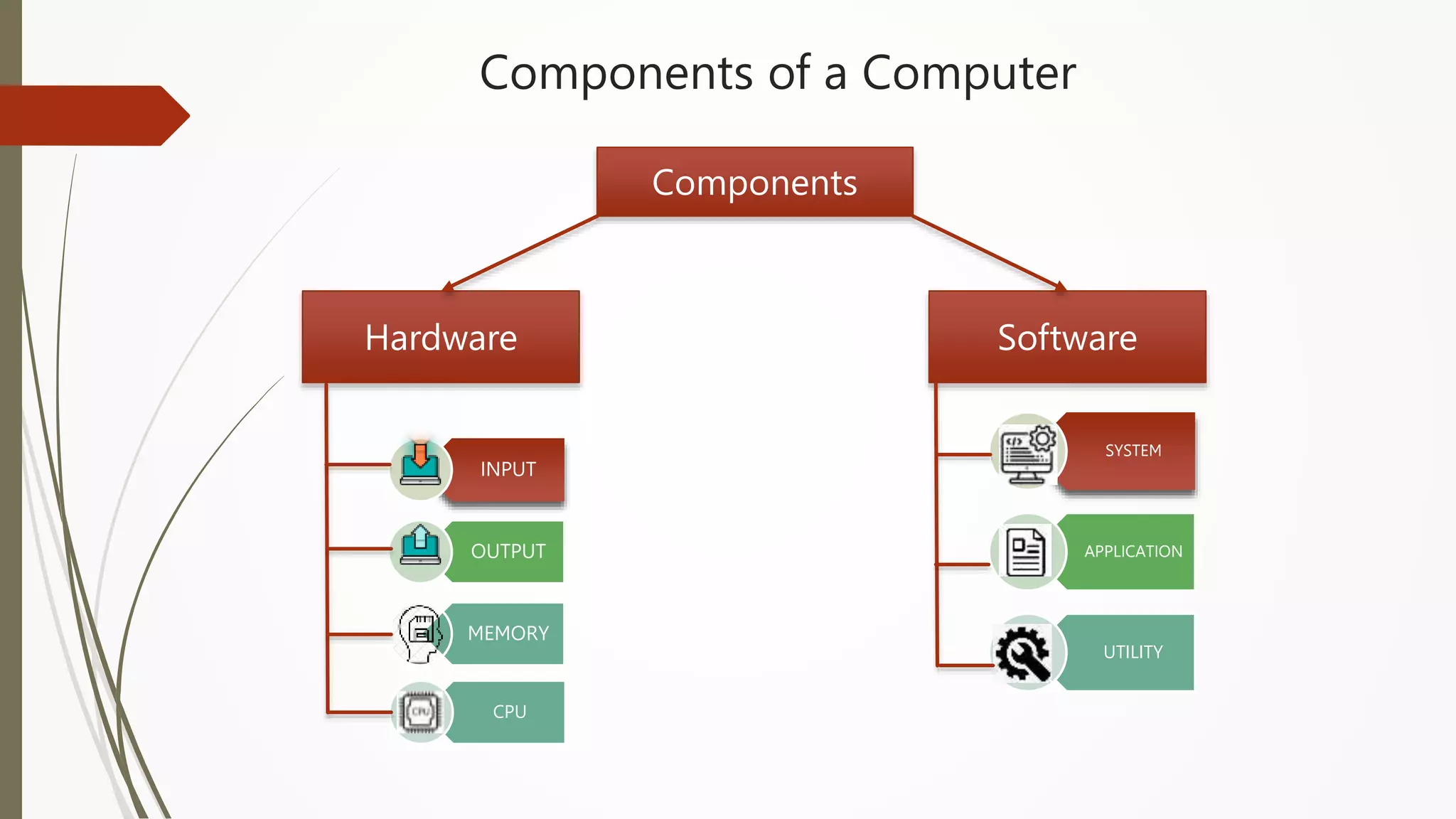
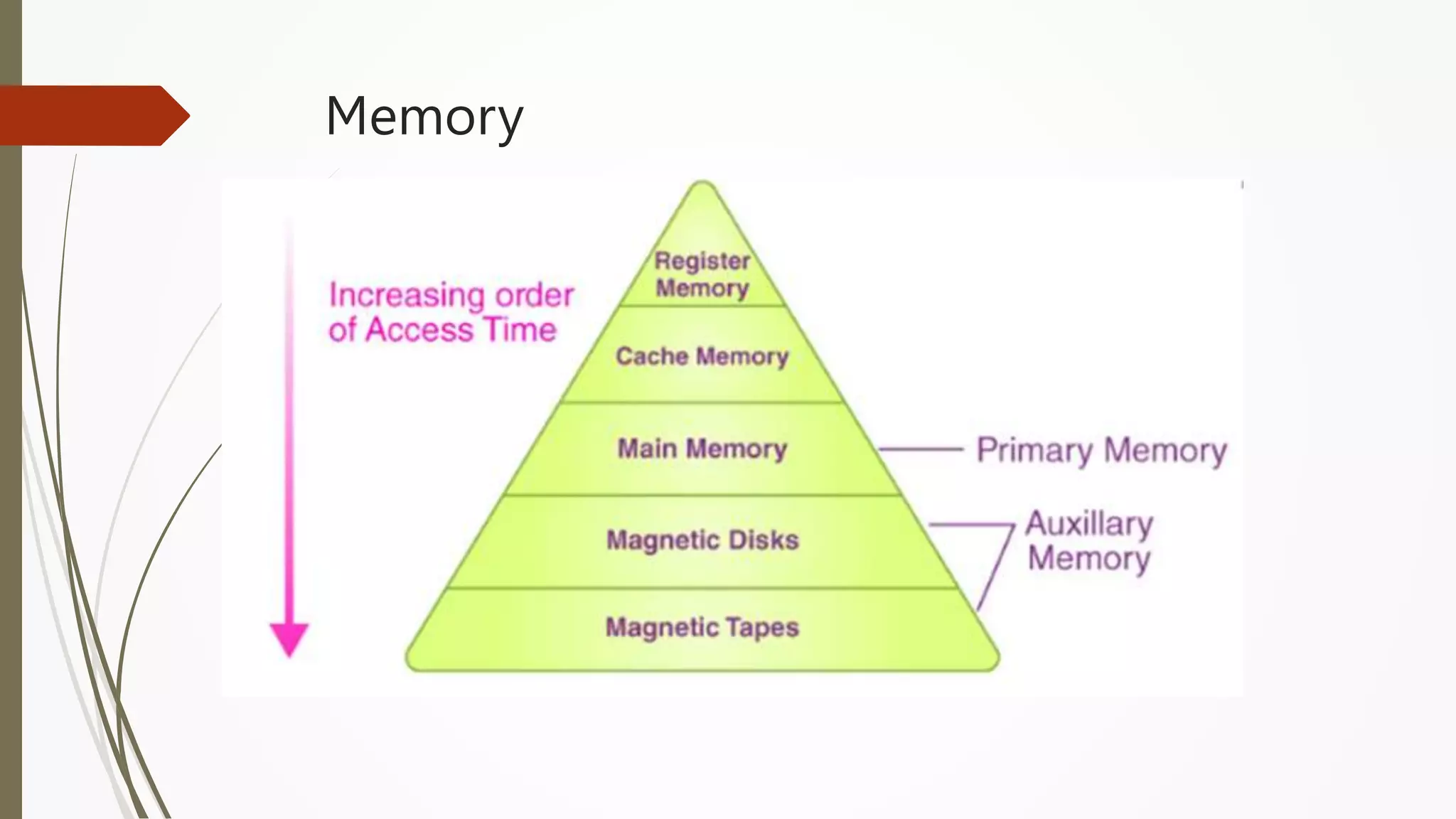
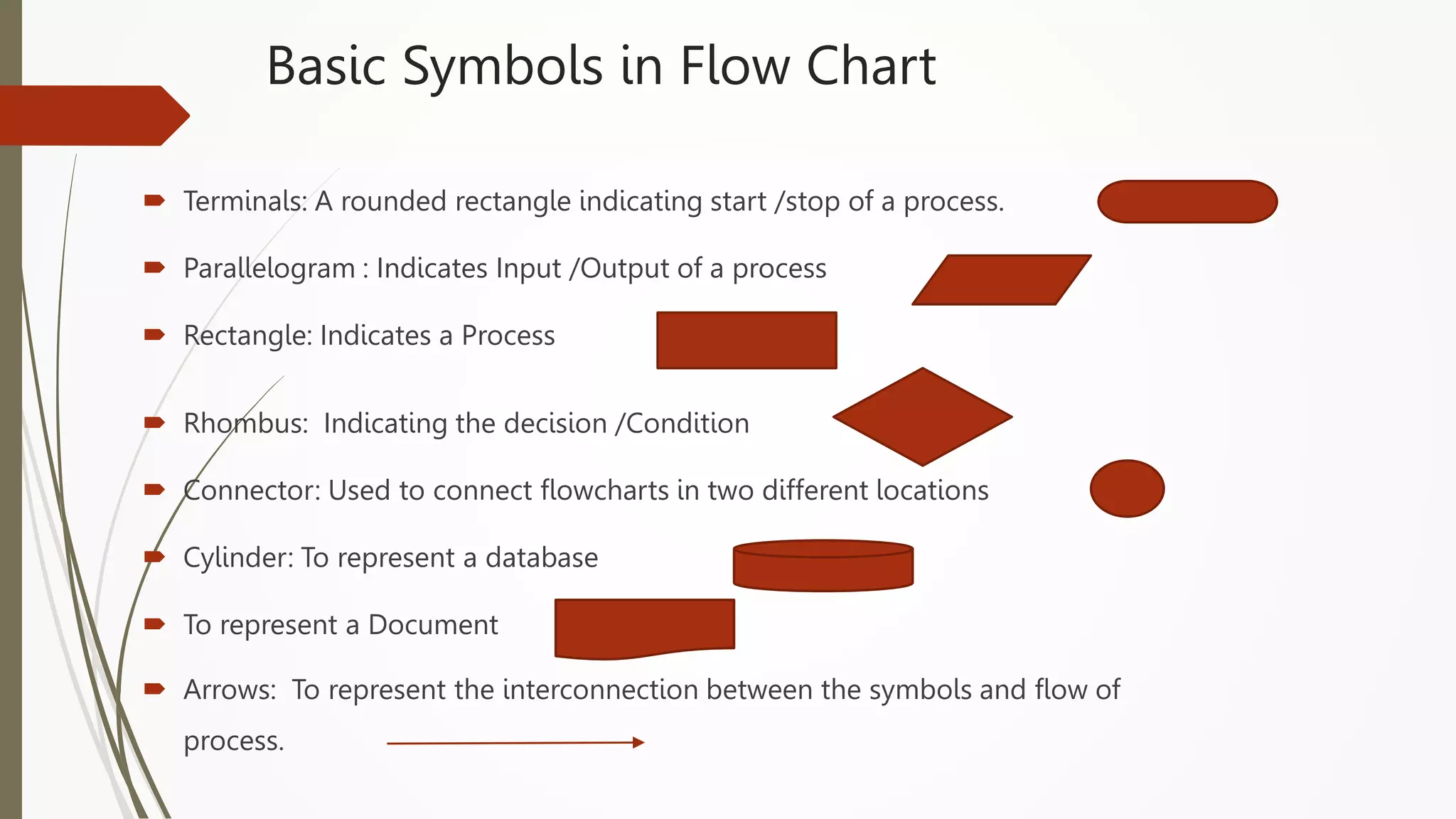
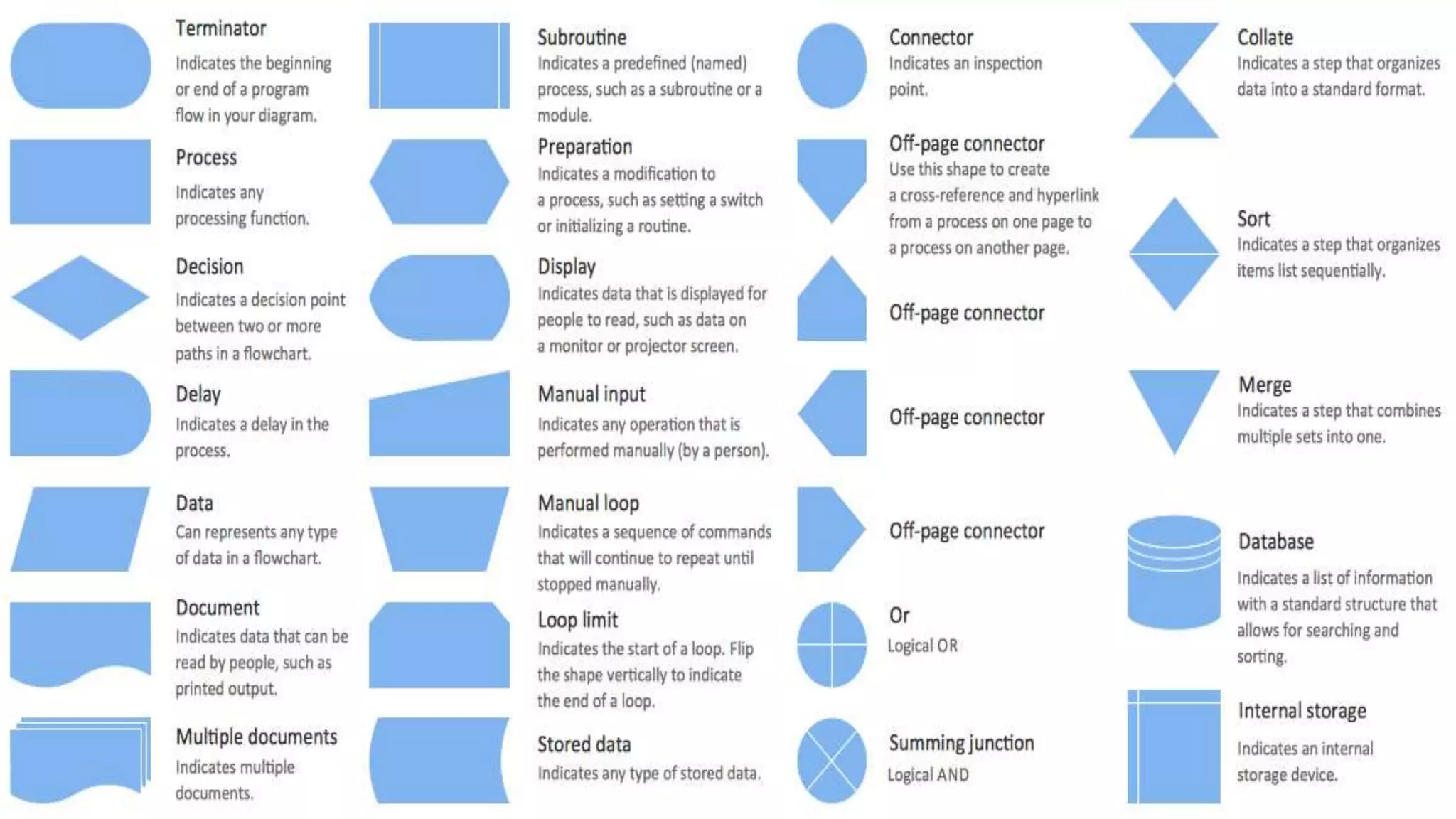
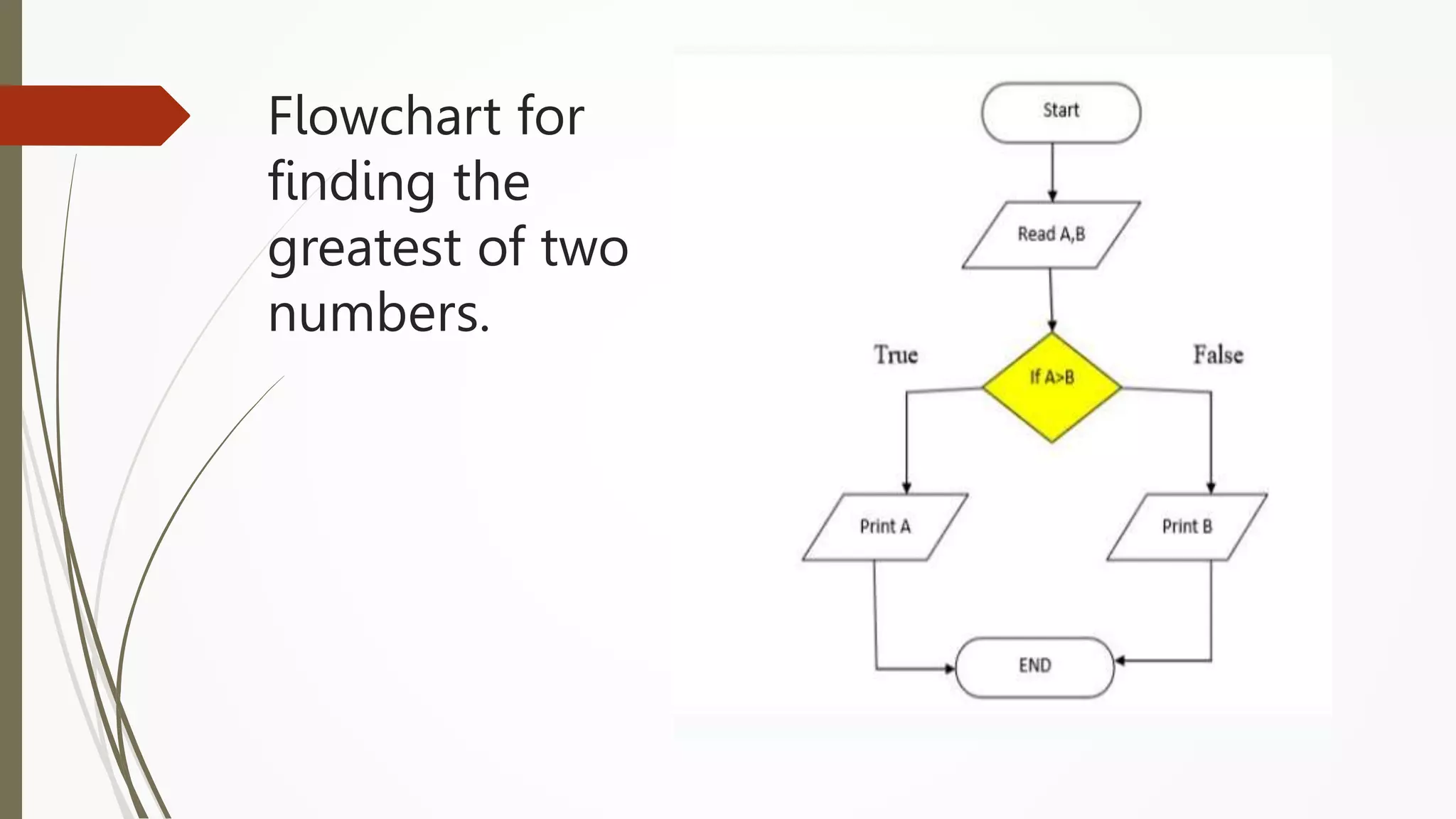
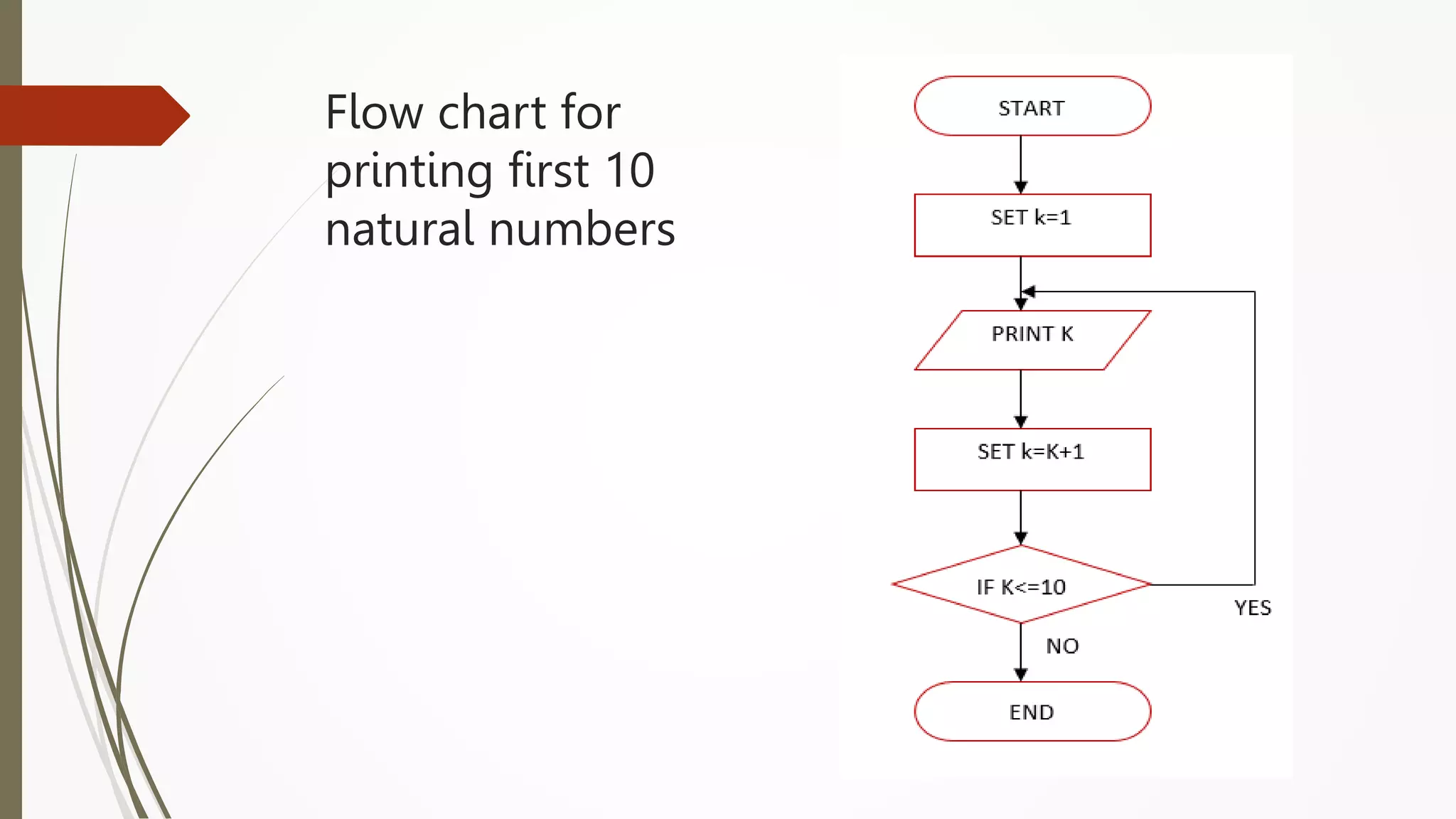
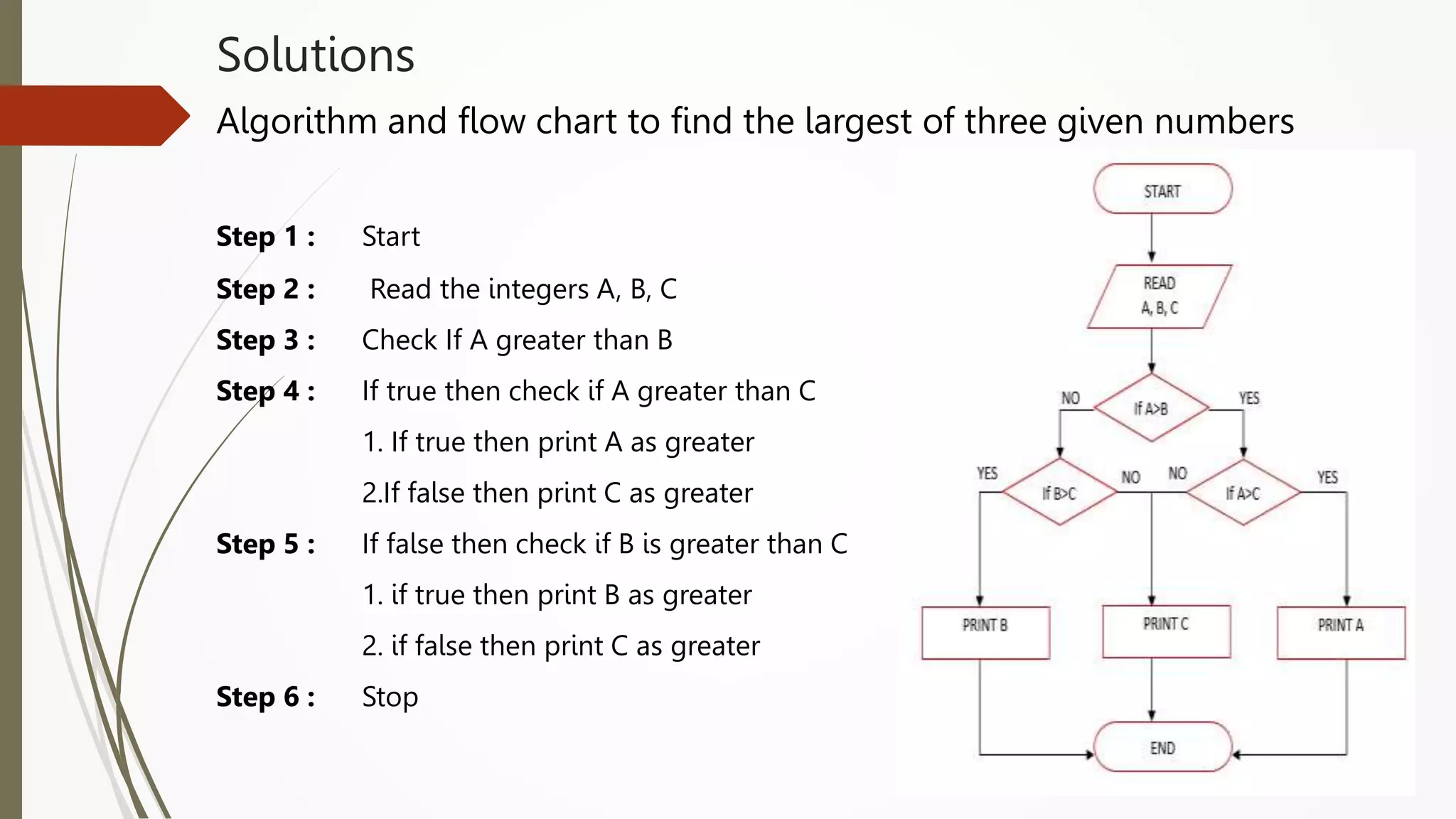
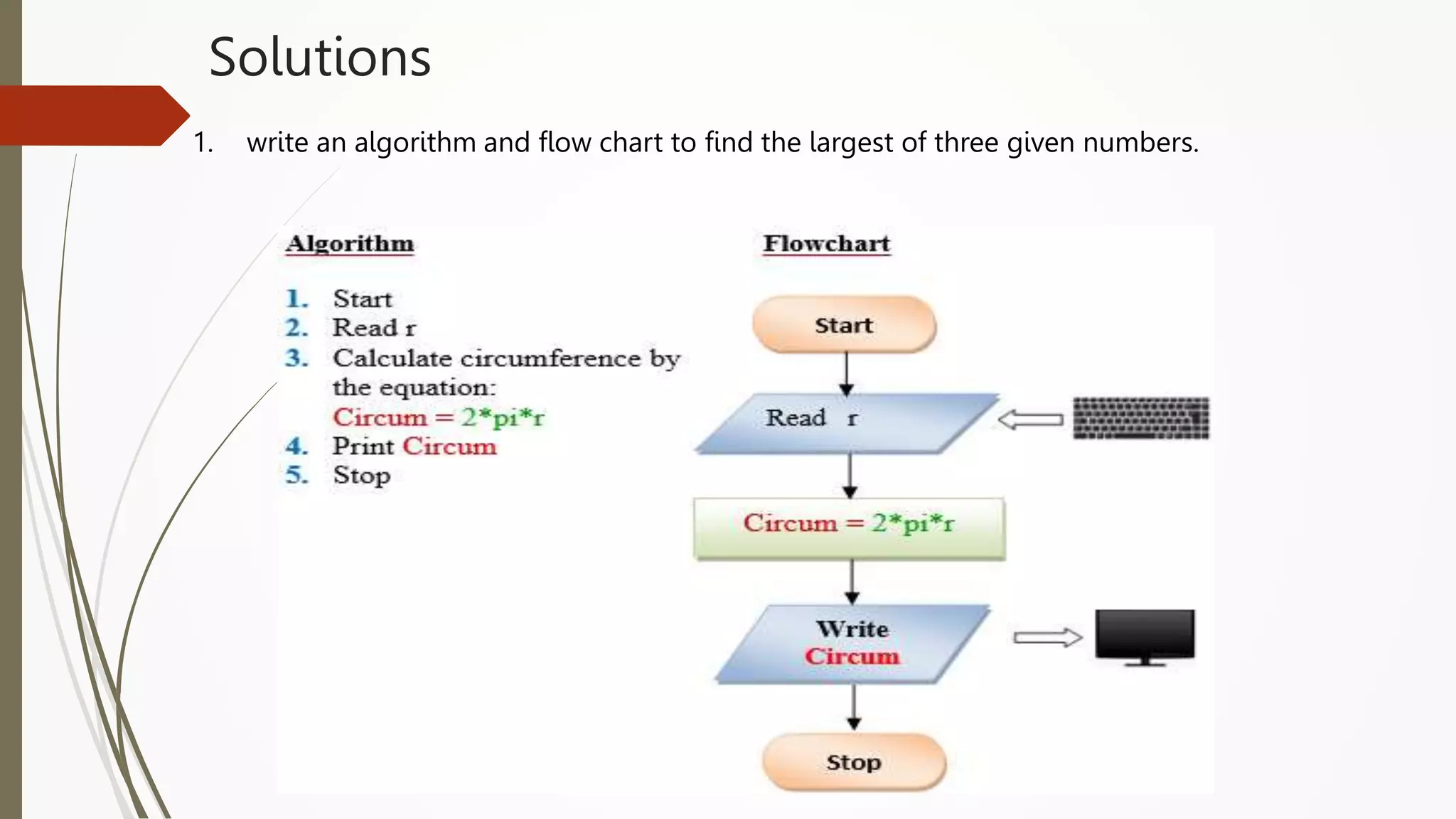
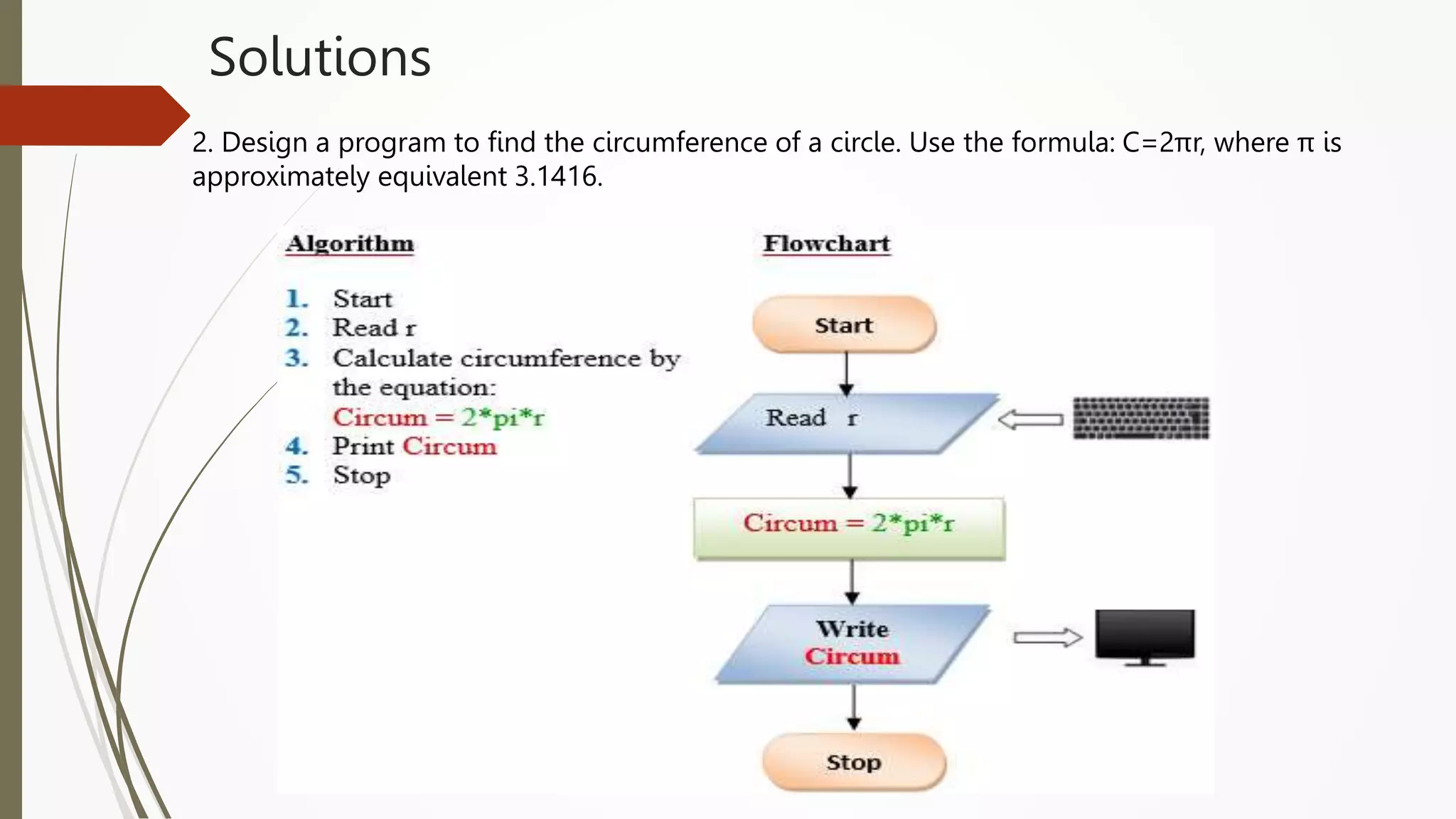
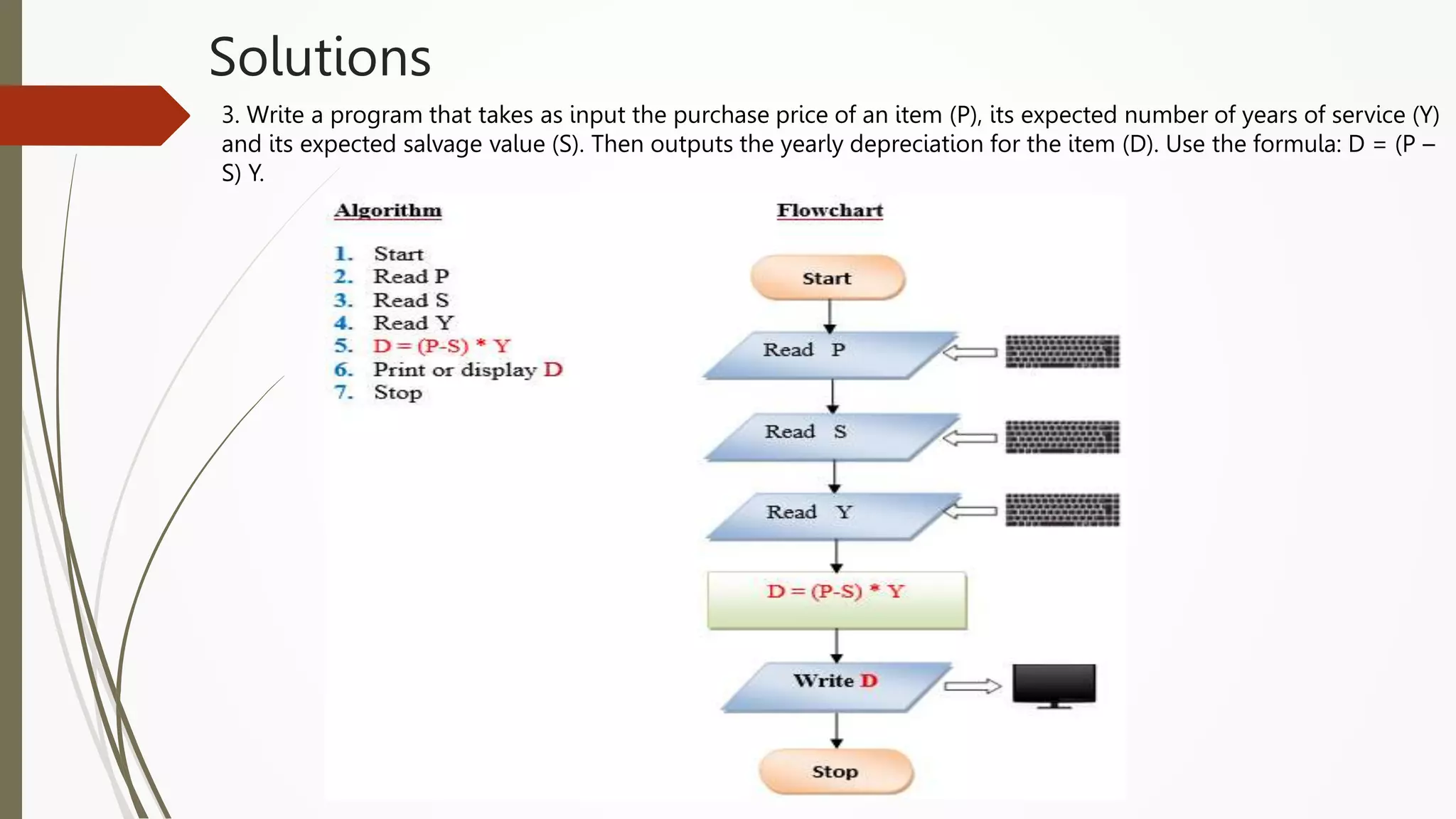
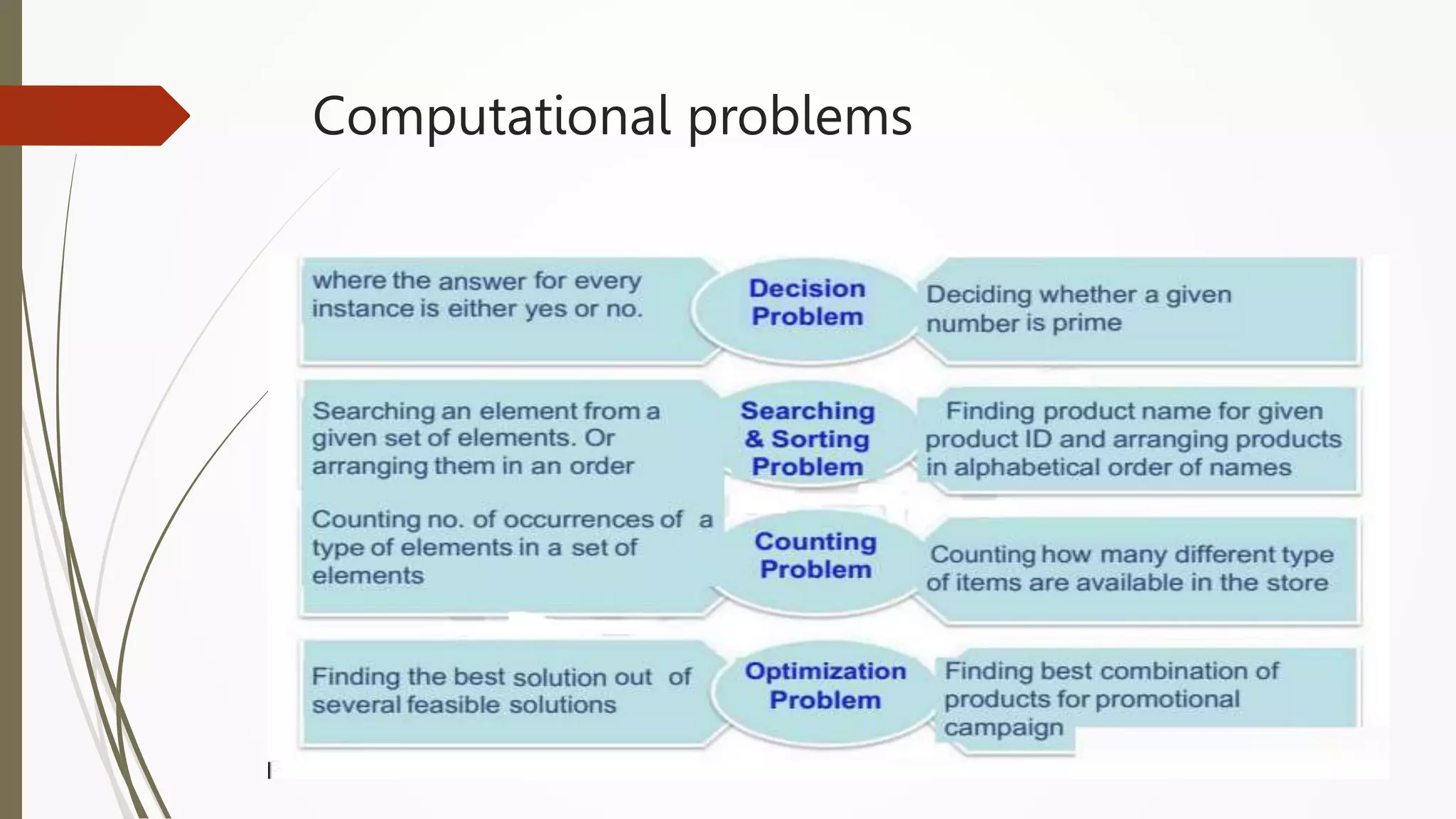
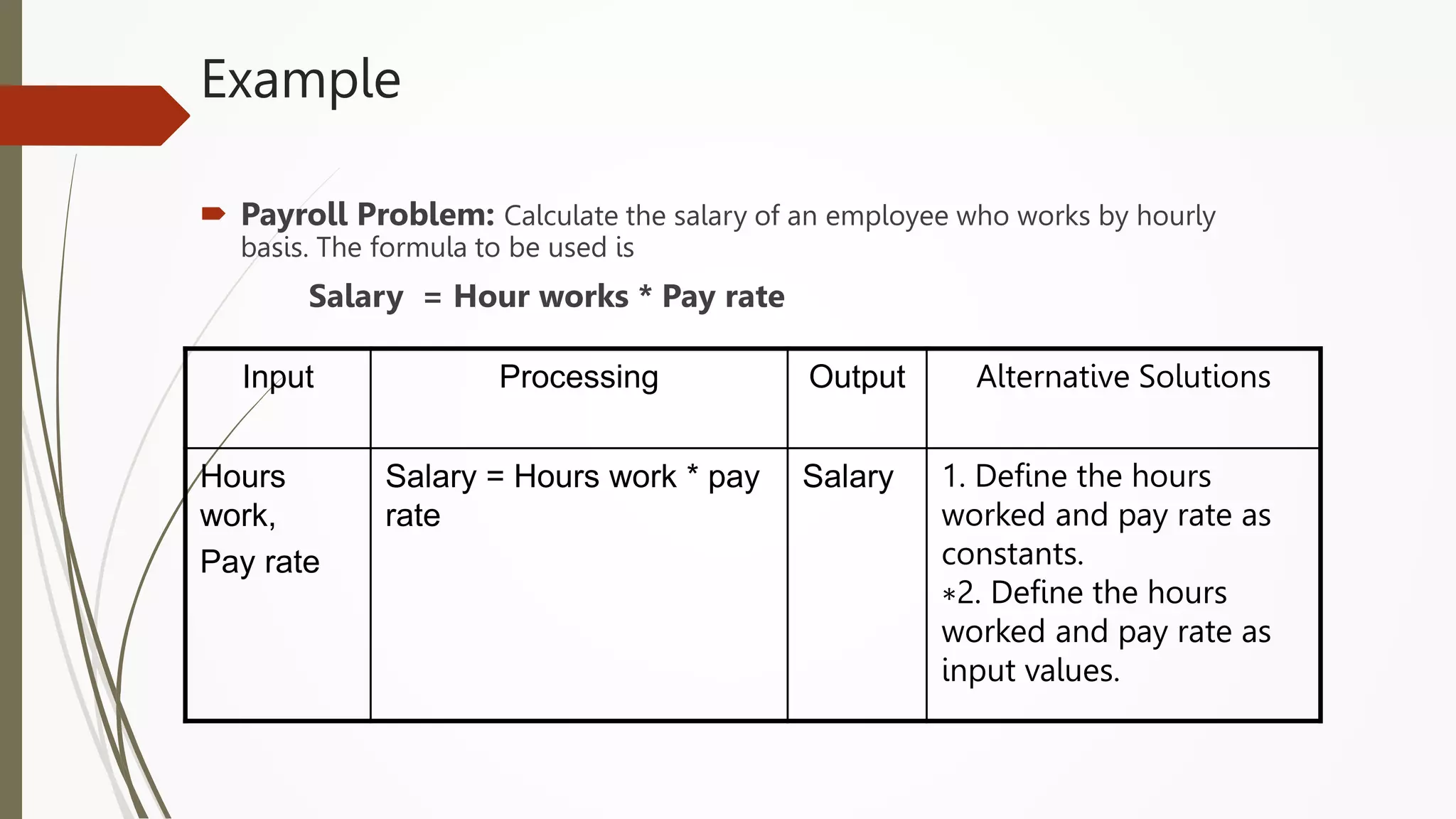
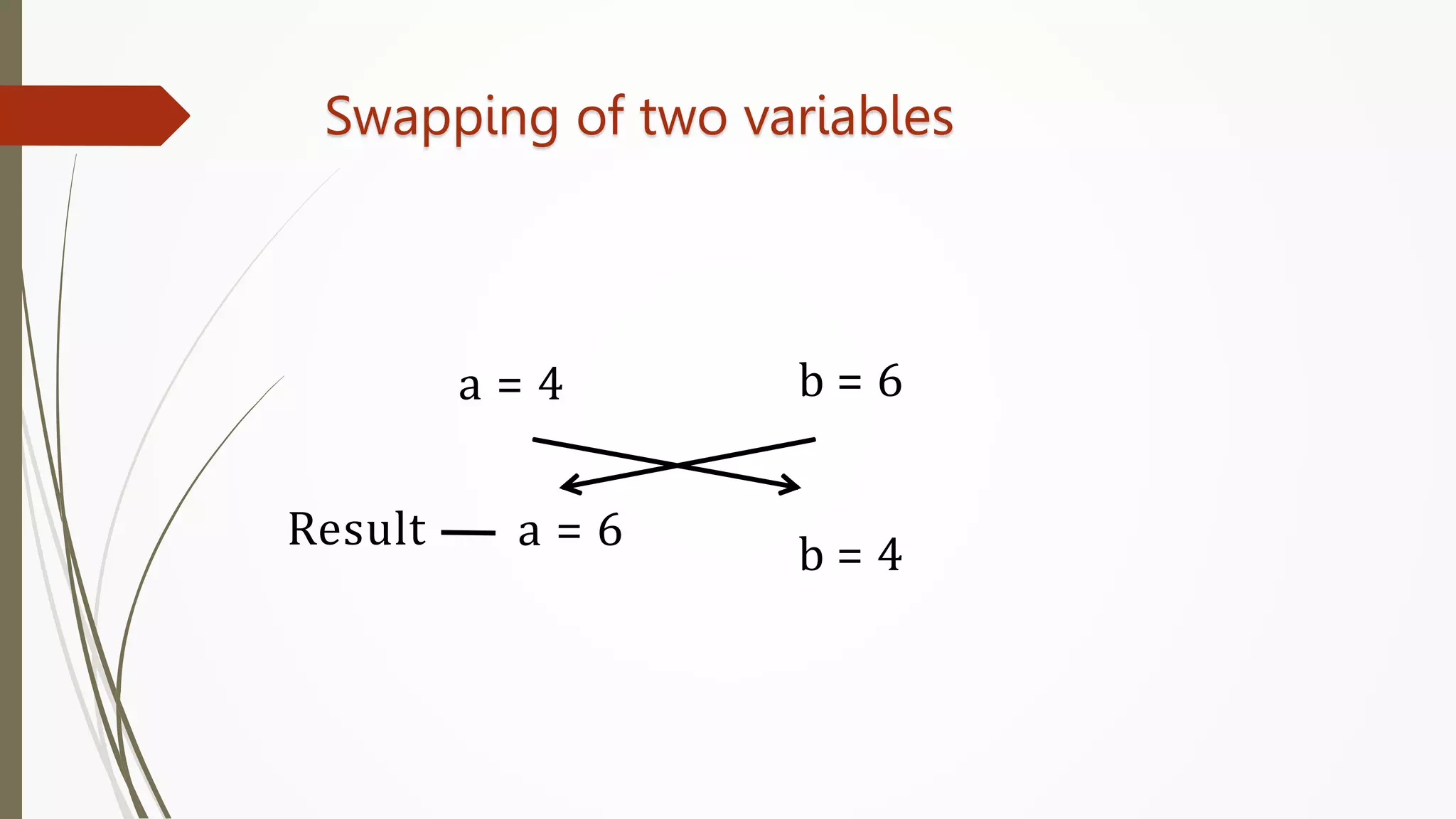
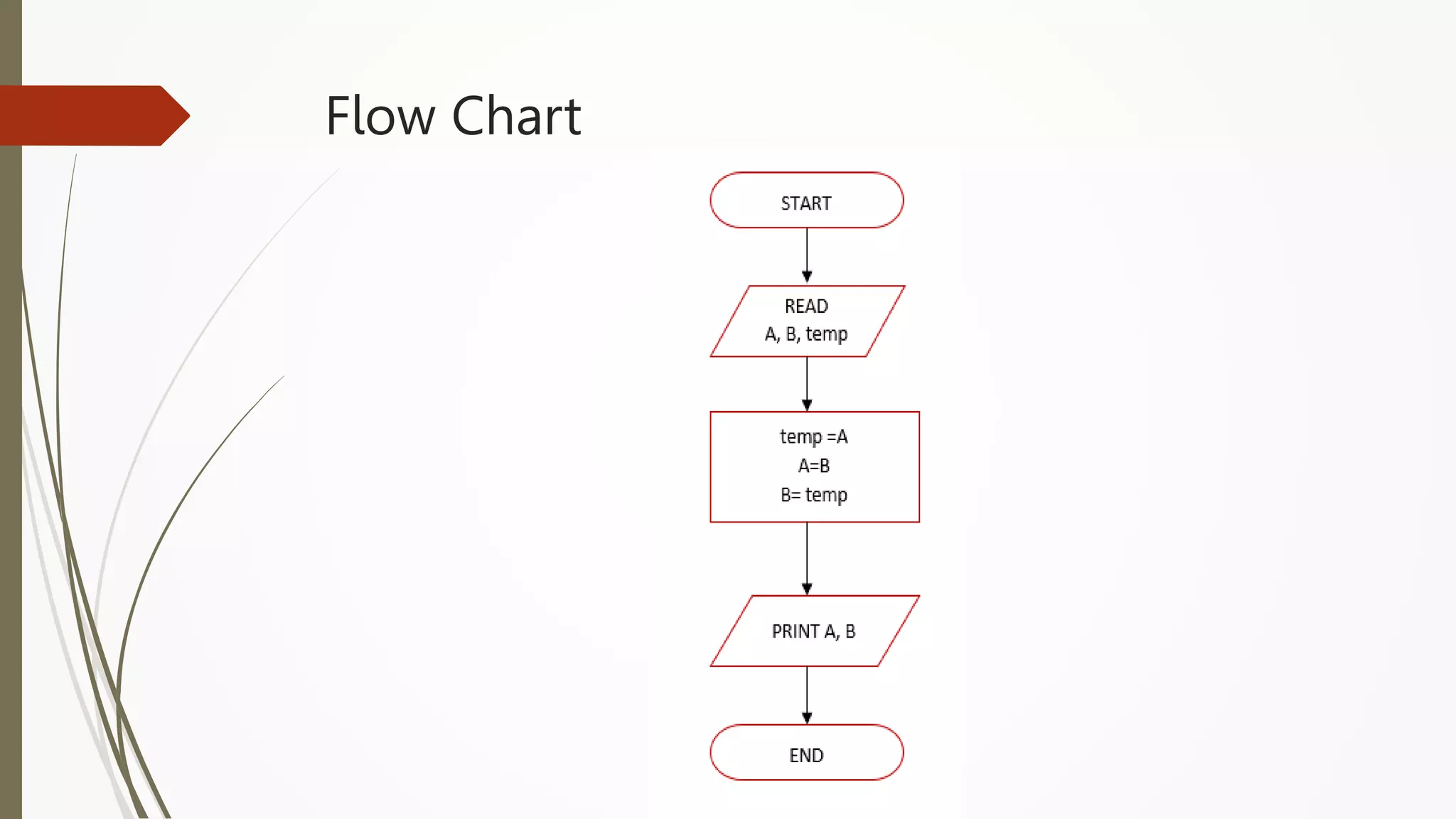
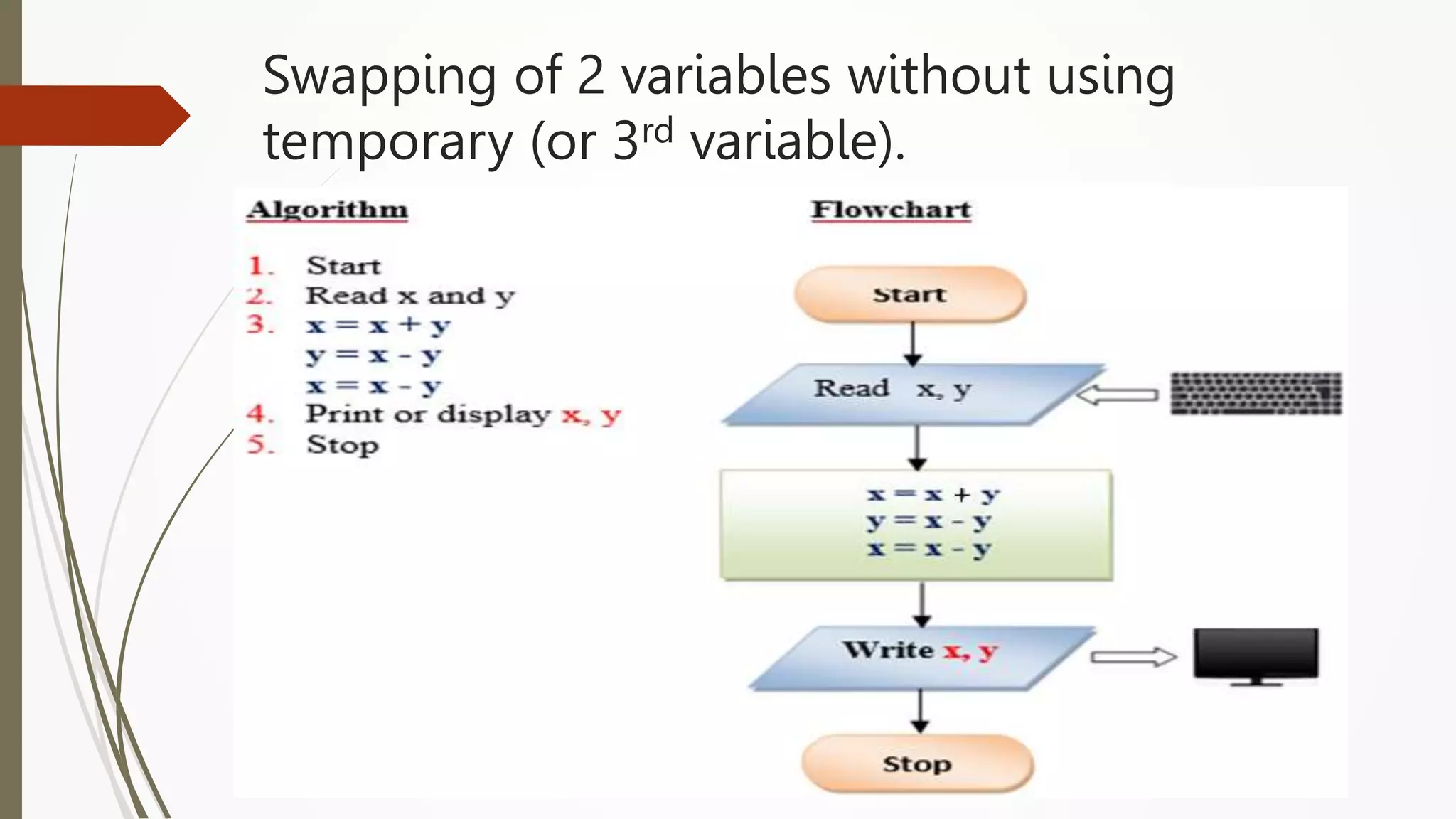
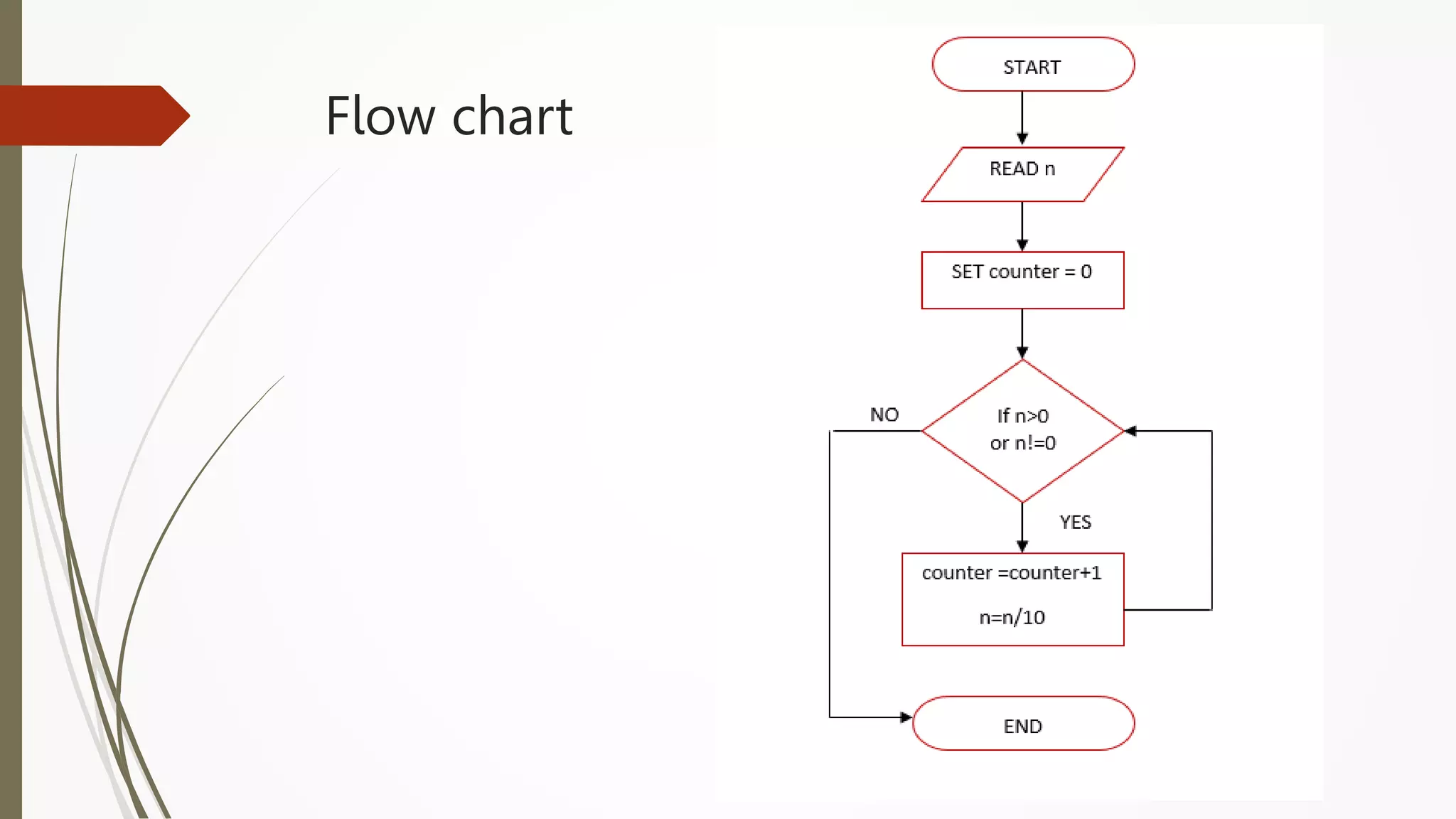
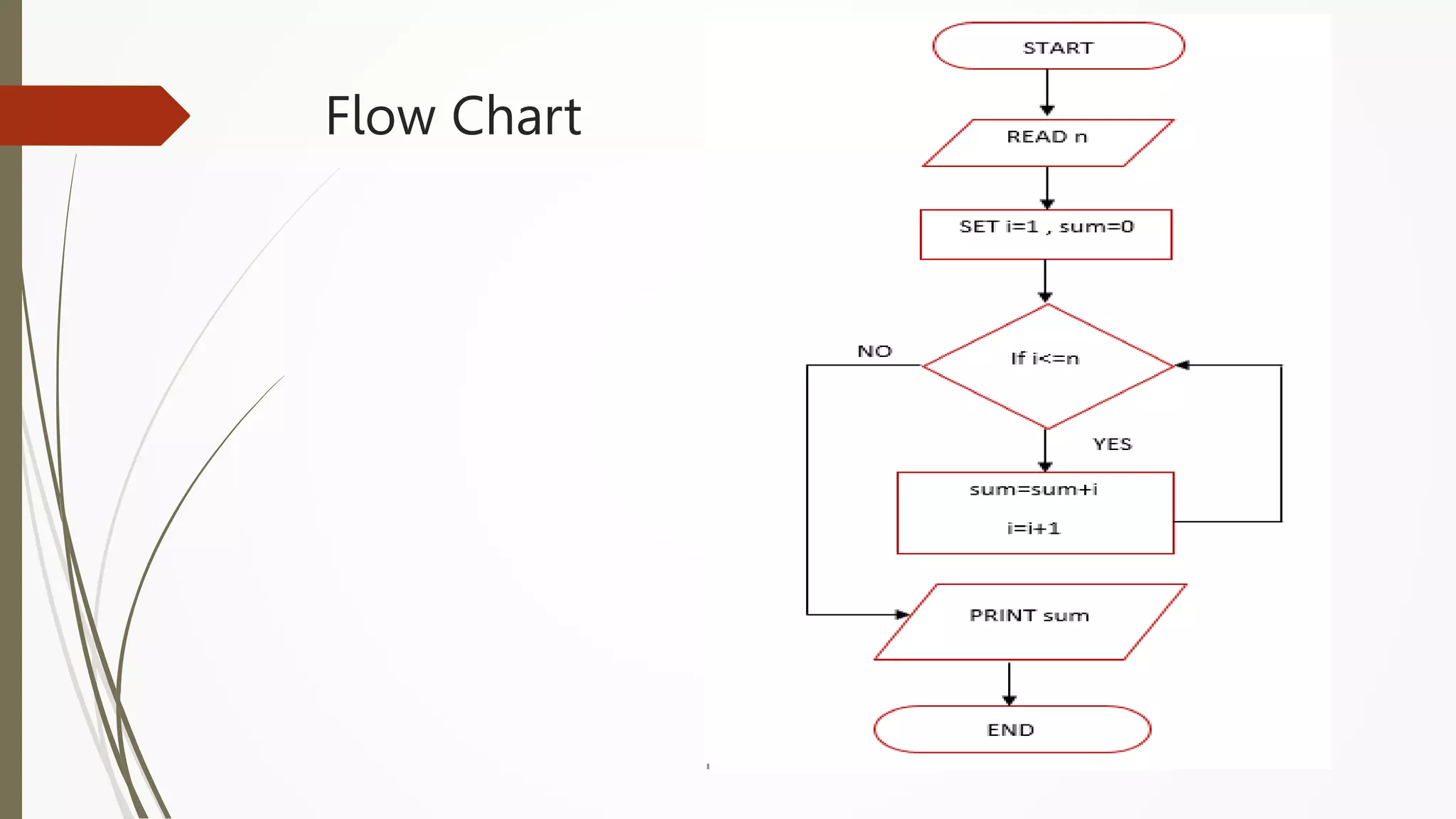
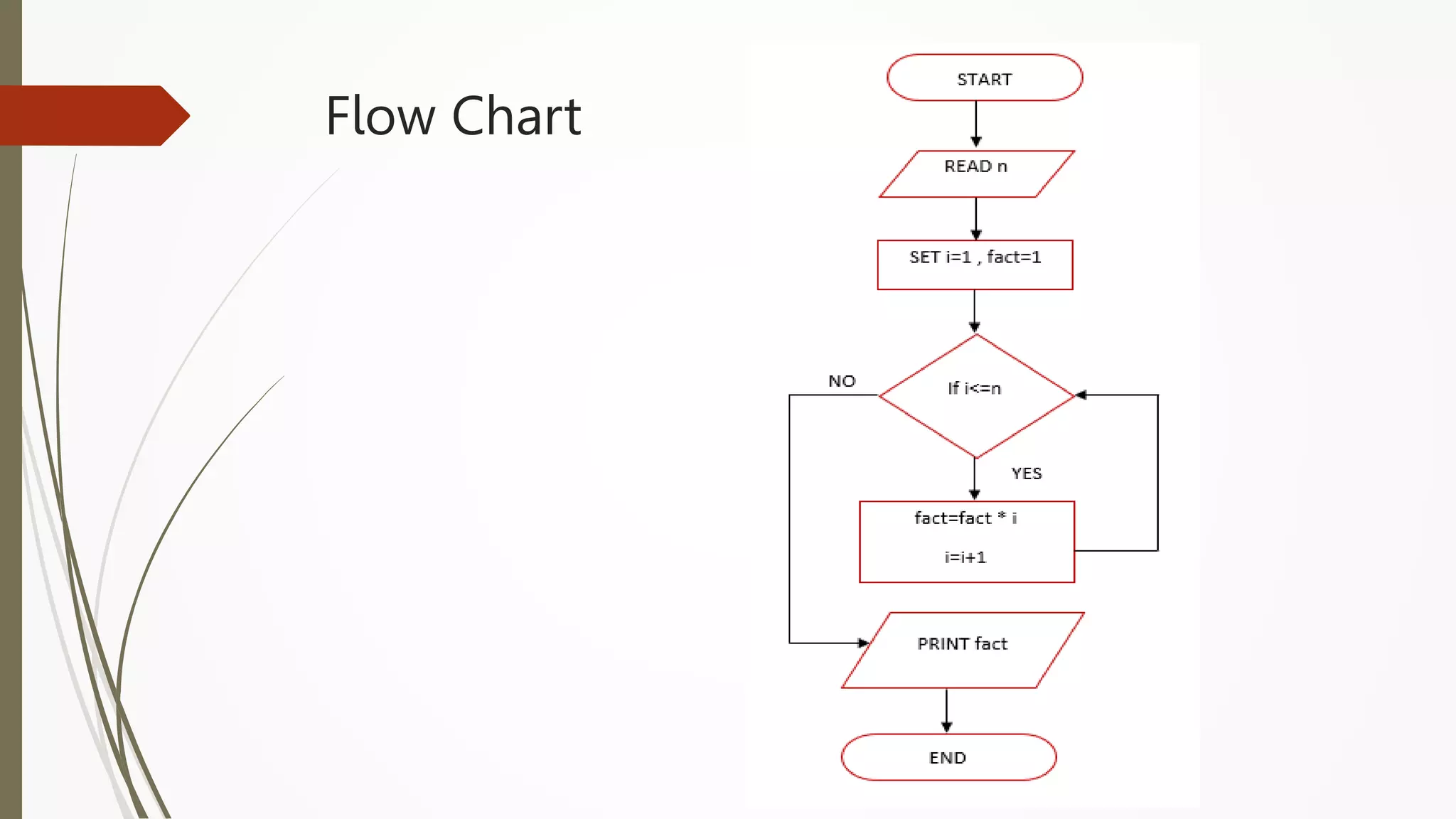
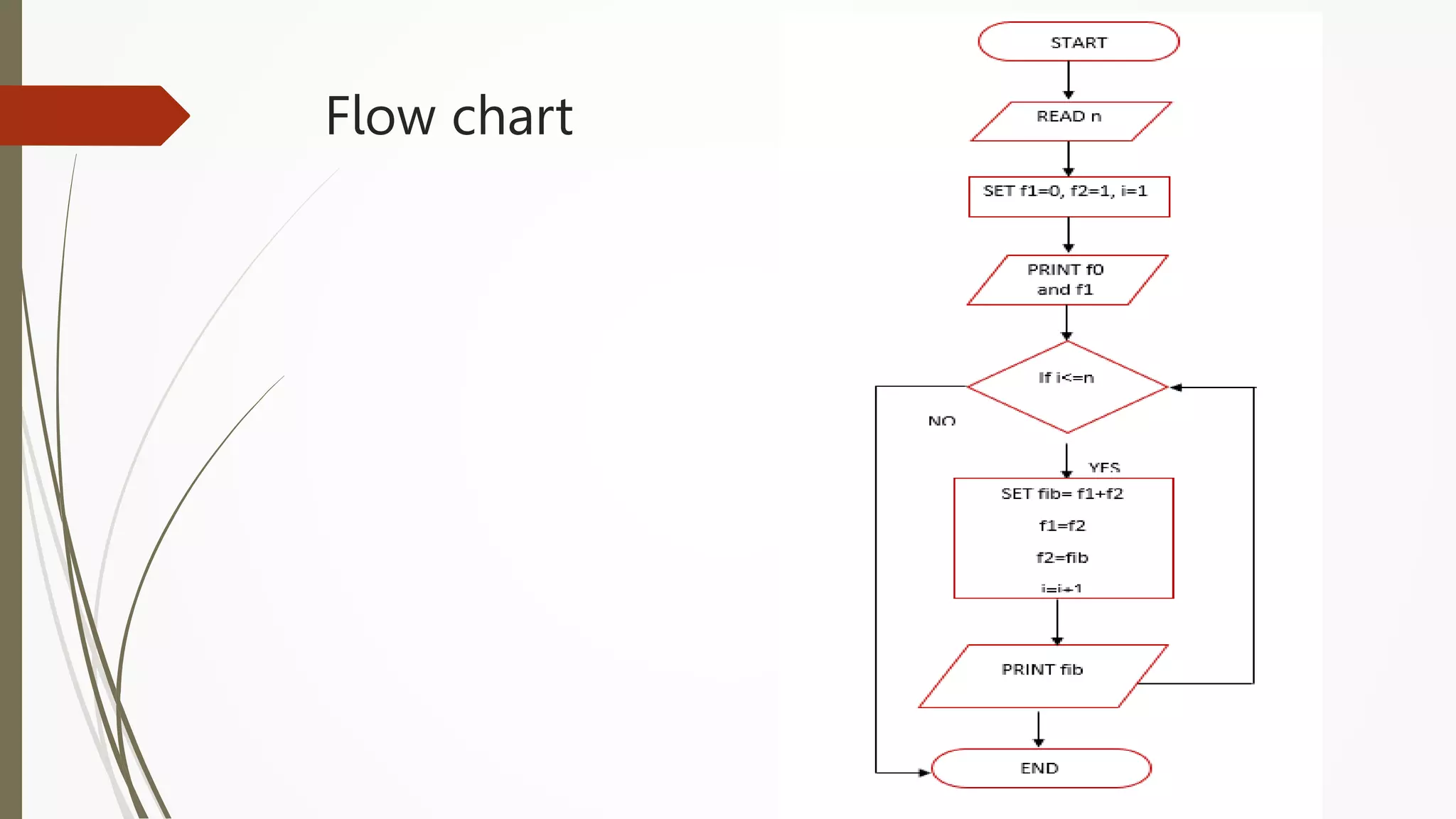
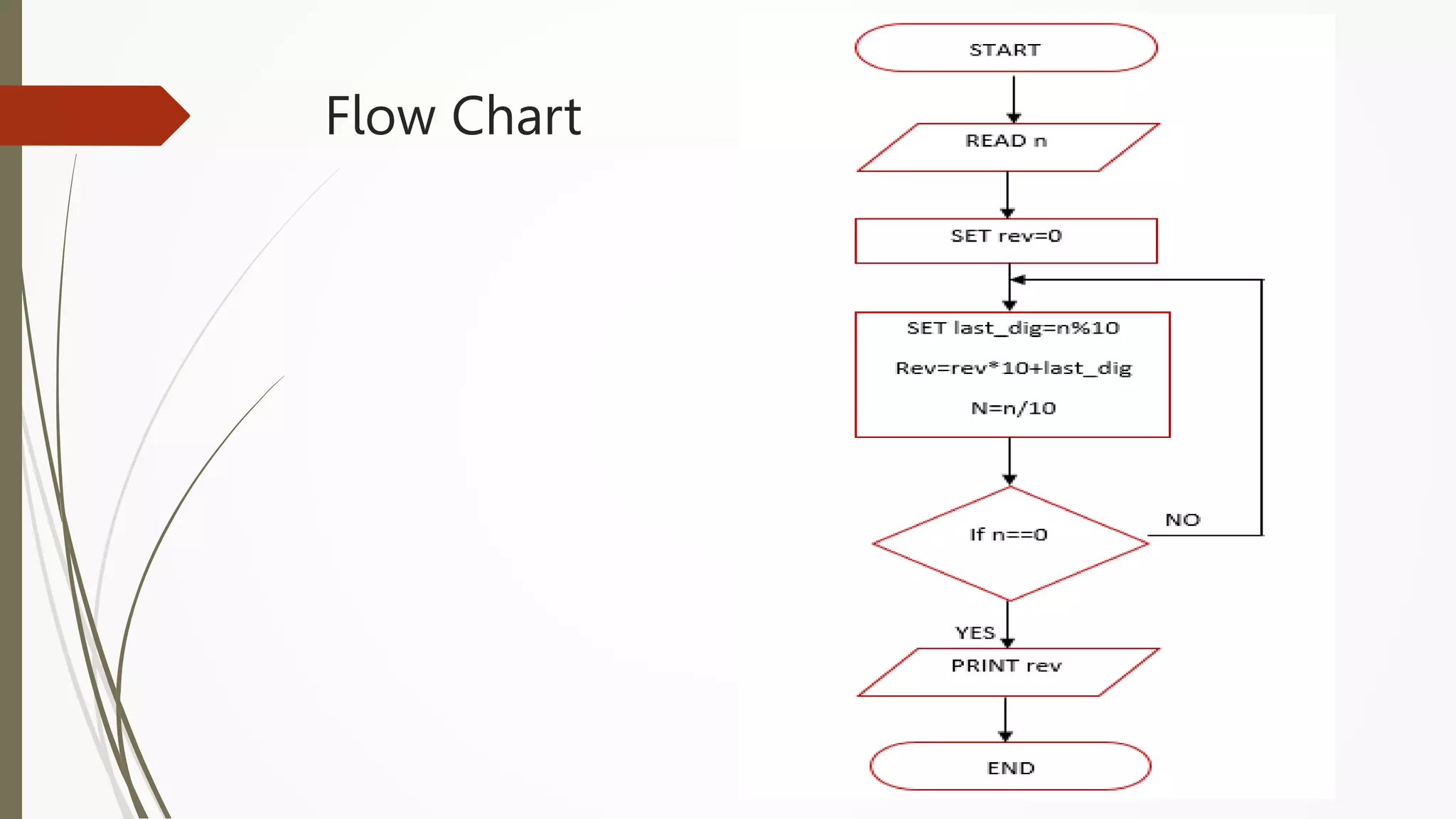
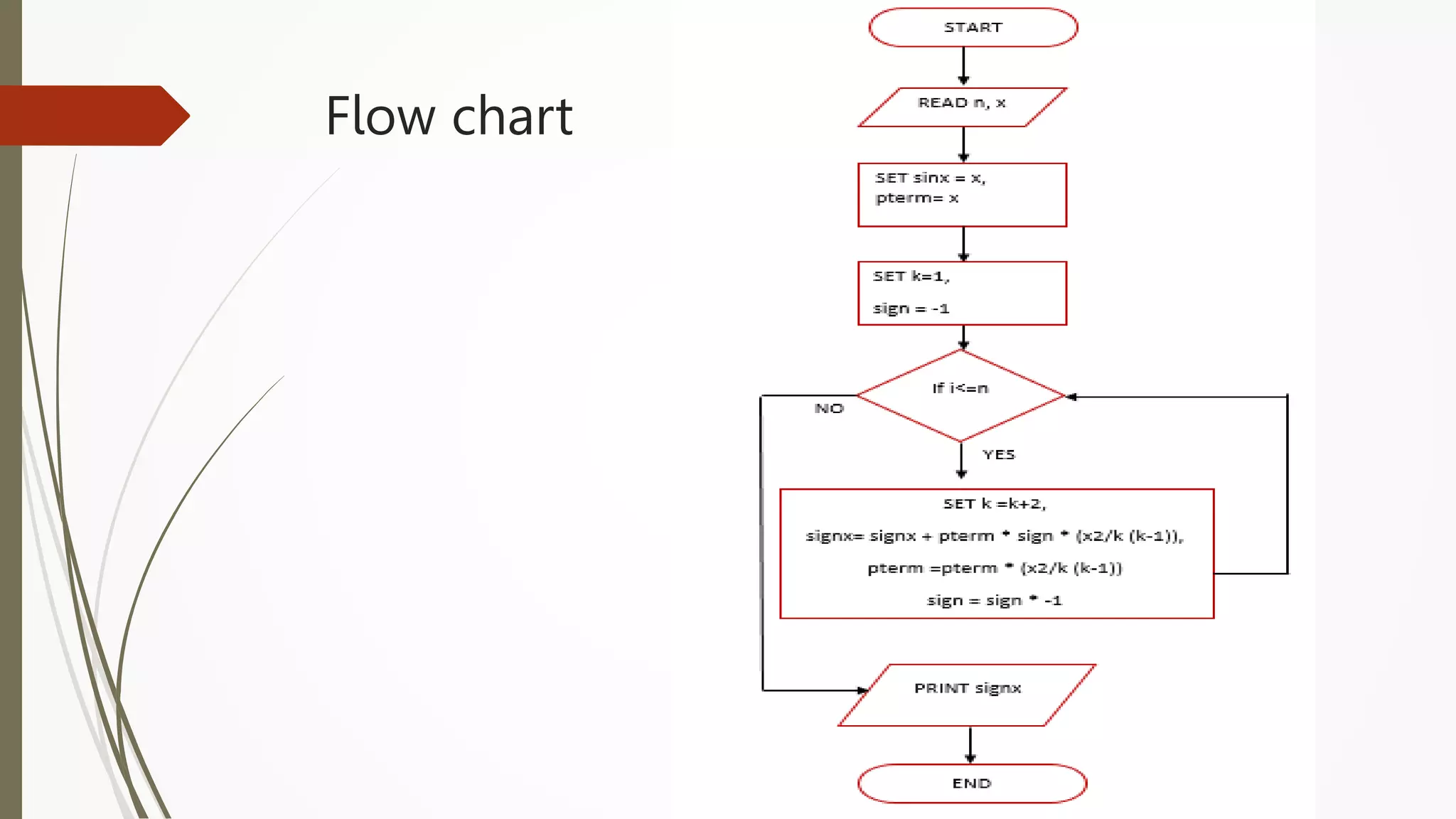
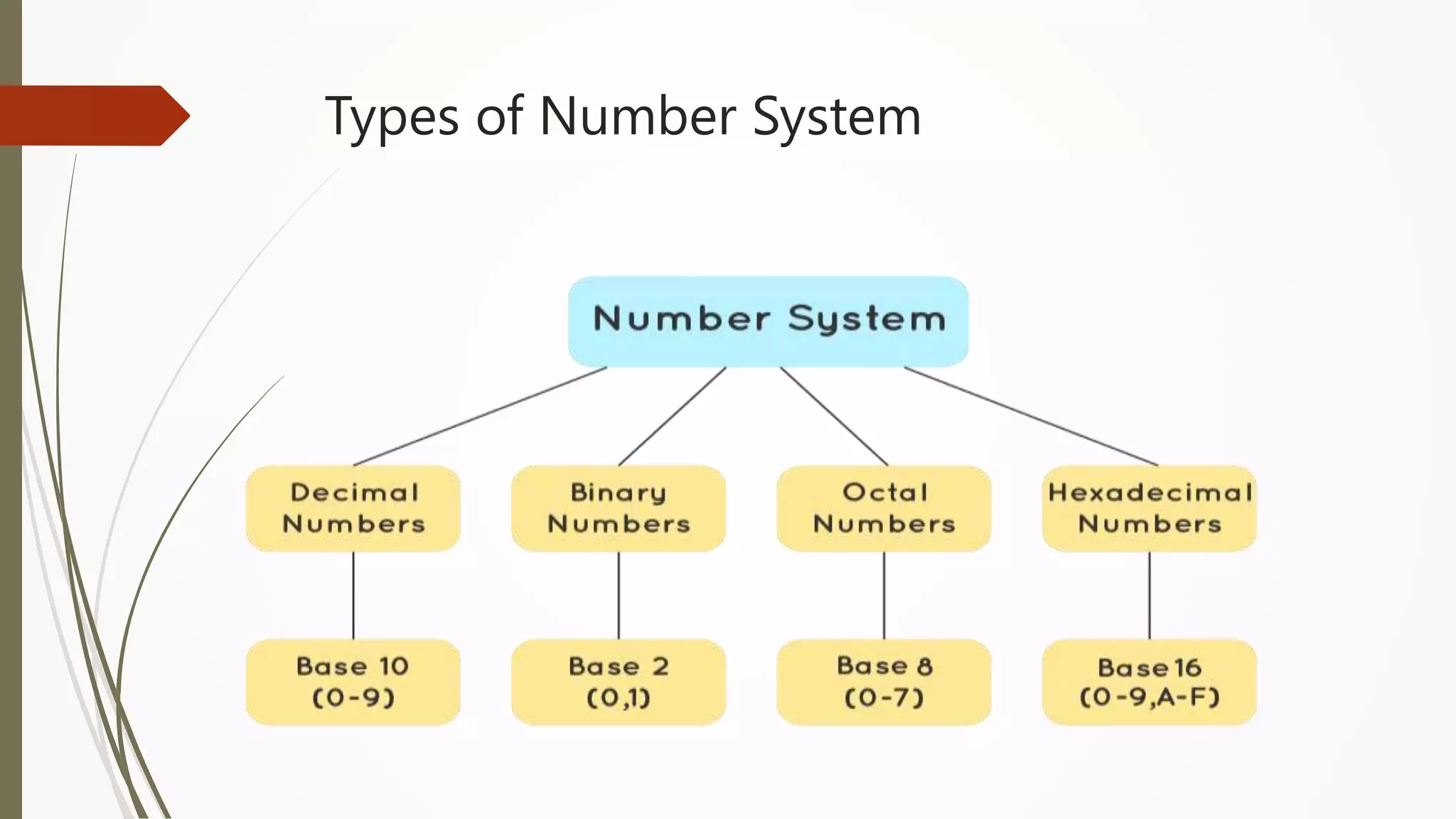
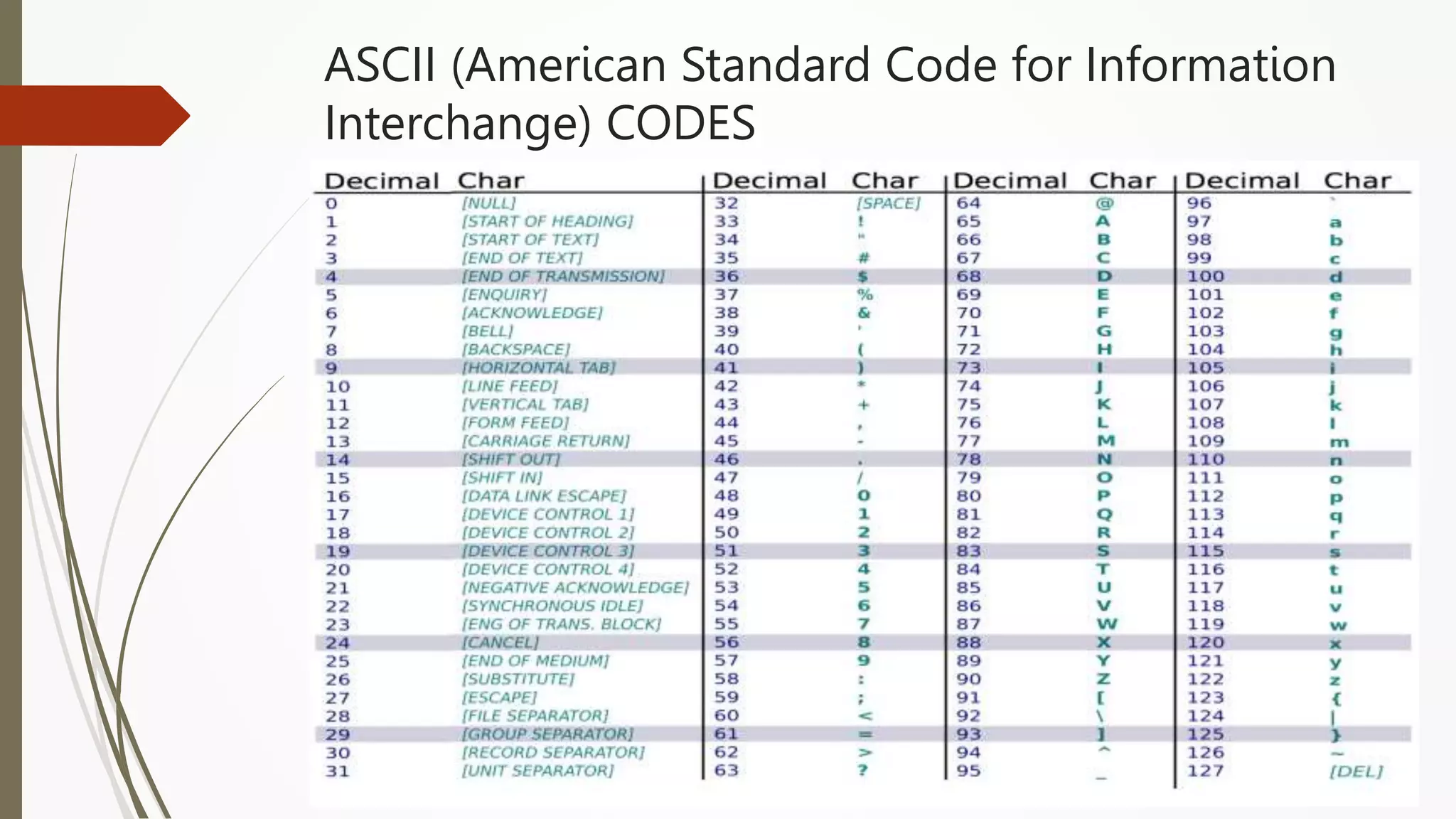
The document provides an introduction to programming in Python. It begins with an overview of the course syllabus which includes topics like problem solving concepts, flow charts, computations involving variables, numbers, and other data types. It then describes the history and generations of computers from the first vacuum tube based computers to modern fifth generation computers using artificial intelligence. It also explains the basic components of a computer including hardware like CPU, memory and software like operating systems, applications and utilities. Finally, it discusses concepts like algorithms, control structures like sequences, decisions and repetitions which are fundamental to programming and problem solving.