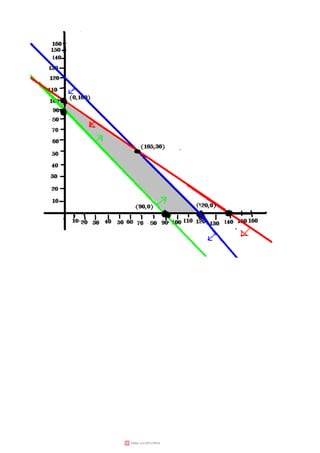
Informe Modelo de programación lineal de dos variable por Juan Carlos Ure Informe Modelo de programación lineal de dos variable por Juan Carlos Ure Informe Modelo de programación lineal de dos variable por Juan Carlos Ure Informe Modelo de programación lineal de dos variable por Juan Carlos Ure Informe Modelo de programación lineal de dos variable por Juan Carlos Ure

1. E
q
u
i
p
od
e
I
n
v
e
s
t
i
g
a
c
i
ó
ny
D
e
s
a
r
r
o
l
l
o
J
u
a
nC
a
r
l
o
s
U
r
e
C
.
I
.
1
1
.
4
2
5
.
7
7
6
A
l
i
c
i
aF
o
n
gC
.
I
.
1
0
.
4
6
7
.
1
1
7
U
CI
n
v
e
s
t
i
g
a
c
i
ó
nd
e
O
p
e
r
a
c
i
o
n
e
s
T
u
t
o
r
(
a
)
a
c
a
d
é
mi
c
a
:
P
r
o
f
.
L
u
i
s
C
o
n
t
r
e
r
a
s
P
N
F
D
L4
3
0
1
B
a
r
q
u
i
s
i
me
t
o
,
J
u
n
i
o2
0
2
2

2. Mo
d
e
l
od
e
p
r
o
g
r
a
ma
c
i
ó
nl
i
n
e
a
l
d
e
d
o
s
v
a
r
i
a
b
l
e
.
E
se
l
c
a
mp
od
el
ap
r
o
g
r
a
ma
c
i
ó
nma
t
e
má
t
i
c
ad
e
d
i
c
a
d
aama
x
i
mi
z
a
romi
n
i
mi
z
a
ru
n
a
f
u
n
c
i
ó
nl
i
n
e
a
l
,
d
e
n
o
mi
n
a
d
af
u
n
c
i
ó
no
b
j
e
t
i
v
od
et
a
l
f
o
r
maq
u
el
av
a
r
i
a
b
l
ed
ed
i
c
h
af
u
n
c
i
ó
n
e
s
t
as
u
j
e
t
aau
n
as
e
r
i
ed
er
e
s
t
r
i
c
c
i
o
n
e
se
x
p
r
e
s
a
d
a
s
me
d
i
a
n
t
eu
ns
i
s
t
e
mad
ee
c
u
a
c
i
o
n
e
so
i
n
e
c
u
a
c
i
o
n
e
s
t
a
mb
i
é
nl
i
n
e
a
l
e
s
.
E
n l
a p
r
o
g
r
a
ma
c
i
ó
n l
i
n
e
a
lP
L c
o
n
s
i
s
t
e e
n o
p
t
i
mi
z
a
ru
n
a f
u
n
c
i
ó
n l
i
n
e
a
ls
u
j
e
t
a a
r
e
s
t
r
i
c
c
i
o
n
e
s
l
i
n
e
a
l
e
s
d
e
v
a
r
i
a
b
l
e
s
r
e
a
l
e
s
.
L
o
smé
t
o
d
o
sd
ep
r
o
g
r
a
ma
c
i
ó
nl
i
n
e
a
l
s
eu
t
i
l
i
z
a
nd
i
f
e
r
e
n
t
e
s
mé
t
o
d
o
s
d
es
o
l
u
c
i
ó
ny
l
o
s
ma
s
d
i
f
u
n
d
i
d
o
s
s
o
nl
o
s
mé
t
o
d
o
s
g
r
á
f
i
c
o
s
y
mé
t
o
d
o
s
s
i
mp
l
e
x
L
o
sp
r
o
b
l
e
ma
sd
es
i
s
t
e
ma
sd
ei
n
e
c
u
a
c
i
ó
nyt
a
mb
i
é
np
r
o
b
l
e
ma
sd
eo
p
t
i
mi
z
a
c
i
ó
n ys
e
r
e
s
u
e
l
v
e
d
e
d
i
f
e
r
e
n
t
e
s
f
o
r
ma
s
.
E
x
i
s
t
ep
r
o
b
l
e
ma
sd
ed
o
si
n
c
ó
g
n
i
t
ae
nd
o
n
d
ed
e
b
e
mo
sma
x
i
mi
z
aomi
n
i
mi
z
a
r
u
n
af
u
n
c
i
ó
n
e
n
d
o
n
d
e
d
e
c
i
mo
s
q
u
e
v
a
mo
s
a
o
p
t
i
mi
z
a
E
s
t
af
u
n
c
i
ó
nl
al
l
a
ma
r
e
mo
sf
u
n
c
i
ó
no
b
j
e
t
i
v
o F (
x
,
y
) l
u
e
g
ol
e
e
r
e
mo
sn
u
e
s
t
r
o
p
r
o
b
l
e
ma
sy v
a
mo
sap
l
a
n
t
e
a
r
q
u
ed
i
c
h
af
u
n
c
i
ó
no
b
j
e
t
i
v
o
,
l
u
e
g
op
l
a
n
t
e
a
r
e
mo
sn
u
e
s
t
r
o
s
i
s
t
e
ma d
ei
n
e
c
u
a
c
i
ó
ny
p
a
r
ae
l
l
o
sn
o
sv
a
mo
saa
y
u
d
a
r
d
eu
n
at
a
b
l
ad
ed
o
b
l
ee
n
t
r
a
d
ay
r
e
s
o
l
v
e
mo
sd
i
c
h
os
i
s
t
e
mac
o
mol
as
o
l
u
c
i
ó
ne
ne
l
p
u
n
t
od
e
l
p
l
a
n
o q
u
es
a
t
i
s
f
a
c
ed
i
c
h
o
s
i
s
t
e
maf
o
r
ma
nu
np
o
l
í
g
o
n
oou
n
ar
e
g
i
ó
np
o
l
i
g
o
n
a
l
s
e
aa
c
o
t
a
d
aon
o a
d
e
má
sp
a
r
al
o
s
p
r
o
b
l
e
ma
sd
ep
r
o
g
r
a
ma
c
i
ó
nl
i
n
e
a
l
d
e
b
e
mo
sc
a
l
c
u
l
a
r
l
o
sv
é
r
t
i
c
e
sd
ed
i
c
h
ar
e
g
i
ó
ns
o
l
u
c
i
ó
n
q
u
e
t
a
mb
i
é
nl
a
l
l
a
ma
r
e
mo
s
r
e
g
i
ó
nf
a
c
t
i
b
l
e
.
C
o
moh
a
l
l
a
r
e
mo
se
s
t
o
sv
é
r
t
i
c
e
s
,
r
e
s
o
l
v
i
e
n
d
os
i
s
t
e
ma
sd
ed
o
se
c
u
a
c
i
o
n
e
sl
i
n
e
a
l
e
sc
o
n
d
o
si
n
c
ó
g
n
i
t
a
sc
o
r
r
e
s
p
o
n
d
i
e
n
t
e
sal
al
í
n
e
ar
e
c
t
aq
u
eh
a
c
eol
oq
u
ef
o
r
mae
s
t
ar
e
g
i
ó
n
f
a
c
t
i
b
l
e
D
i
c
h
ov
é
r
t
i
c
e
ss
o
np
o
s
i
b
l
e
ss
o
l
u
c
i
o
n
e
sys
e
r
á
ns
o
l
u
c
i
ó
naa
q
u
e
l
l
aq
u
eo
p
t
i
mi
c
en
u
e
s
t
r
a
f
u
n
c
i
ó
no
b
j
e
t
i
v
oe
s
d
e
c
i
r
q
u
e
l
ama
x
i
mi
c
e
ol
a
mi
n
i
mi
c
e
s
e
g
ú
ne
l
c
a
s
o
.
S
i
e
x
i
s
t
eu
n
aú
n
i
c
as
o
l
u
c
i
ó
nq
u
es
ee
n
c
u
e
n
t
r
ae
nu
nv
é
r
t
i
c
ed
el
ar
e
g
i
ó
nf
a
c
t
i
b
l
es
i
e
x
i
s
t
e
i
n
f
i
n
i
t
a
s
s
o
l
u
c
i
o
n
e
s
e
e
n
c
u
e
n
t
r
a
e
nu
n
o
s
d
e
l
o
s
l
a
d
od
e
d
i
c
h
a
r
e
g
i
ó
n
.
V
a
mo
sar
e
s
o
l
v
e
r
u
np
r
o
b
l
e
mad
eo
p
t
i
mi
z
a
c
i
ó
nd
ep
r
o
g
r
a
ma
c
i
ó
nl
i
n
e
a
l
p
e
r
o
r
e
c
o
r
d
a
mo
s
q
u
ed
e
b
e
mo
sl
e
e
rb
i
e
n e
l
p
r
o
b
l
e
map
a
r
ap
l
a
n
t
e
a
rn
u
e
s
t
r
af
u
n
c
i
ó
no
b
j
e
t
i
v
ayt
a
mb
i
é
n
n
u
e
s
t
r
os
i
s
t
e
ma
d
e
i
n
e
c
u
a
c
i
o
n
e
s
)
E
j
e
mp
l
o
U
n
a ma
q
u
i
n
a p
r
o
d
u
c
e d
o
s t
i
p
o
s d
e
c
o
mp
u
t
a
d
o
r
a A yB
,p
a
r
a f
a
b
r
i
c
a
r
l
o
ss
e
n
e
c
e
s
i
t
a u
n t
i
e
mp
o d
e p
r
o
d
u
c
c
i
ó
n e
n
ma
q
u
i
n
a
s y u
n a
c
a
b
a
d
o a ma
n
o q
u
e
r
e
a
l
i
z
a
nl
o
so
p
e
r
a
r
i
o
s
.
L
av
e
n
t
ad
e
l
mo
d
e
l
o
An
e
c
e
s
i
t
a2h
o
r
a
se
nl
ama
q
u
i
n
a
sy
me
d
i
a
h
o
r
a d
e t
r
a
b
a
j
o a ma
n
o y p
r
o
d
u
c
e u
n
b
e
n
e
f
i
c
i
od
e6
0
$
.
L
av
e
n
t
ad
e
l
mo
d
e
l
oB
n
e
c
e
s
i
t
a 3 h
o
r
a
s e
n l
a ma
q
u
i
n
a
s y u
n
c
u
a
r
t
od
eh
o
r
ad
et
r
a
b
a
j
oama
n
oyo
r
i
g
i
n
a
u
n
b
e
n
e
f
i
c
i
od
e
5
5
$
.
S
ed
i
s
p
o
n
eu
nt
o
t
a
l
d
e3
0
0h
o
r
a
s
d
et
r
a
b
a
j
o
e
nma
q
u
i
n
a
sy
6
0h
o
r
a
sd
et
r
a
b
a
j
oama
n
o
.
E
n
t
r
el
o
sd
o
st
i
p
o
sd
ec
o
mp
u
t
a
d
o
r
ah
a
nd
e
C
o
mp
u
t
a
d
o
r
a
T
r
a
b
a
j
oa
ma
q
u
i
n
a
(
h
o
r
a
s
)
T
r
a
b
a
j
oa
ma
n
o
(
h
o
r
a
s
)
B
e
n
e
f
i
c
i
o
(
D
ó
l
a
r
e
s
)
A x
B y
T
o
t
a
l
:

3. f
a
b
r
i
c
a
r
s
ep
o
r
l
ome
n
o
s9
0
.
¿
Q
u
éc
a
n
t
i
d
a
d
d
e c
o
mp
u
t
a
d
o
r
a d
e c
a
d
a t
i
p
o h
a d
e
p
r
o
d
u
c
i
r
s
e
p
a
r
a
b
e
n
e
f
i
c
i
os
e
a
má
x
i
mo
?
C
o
mp
u
t
a
d
o
r
a
T
r
a
b
a
j
oama
q
u
i
n
a
(
h
o
r
a
s
)
T
r
a
b
a
j
oama
n
o
(
h
o
r
a
s
)
B
e
n
e
f
i
c
i
o
(
D
ó
l
a
r
e
s
)
A x 2 ½ 6
0
B y 3 ¼ 5
5
T
o
t
a
l
: 3
0
0 6
0 B(
x
,
y
)
T
e
n
i
e
n
d
oe
l
o
r
d
e
n
a
d
ol
o
sd
a
t
o
se
nu
n
at
a
b
l
ad
ed
o
b
l
ee
n
t
r
a
d
av
a
mo
sa
h
o
r
aap
l
a
n
t
e
a
r
n
u
e
s
t
r
a
f
u
n
c
i
ó
no
b
j
e
t
i
v
oe
nn
u
e
s
t
r
os
i
s
t
e
ma
d
e
i
n
e
c
u
a
c
i
o
n
e
s
.
R
e
c
o
r
d
a
mo
sq
u
el
af
u
n
c
i
ó
nq
u
en
o
sp
i
d
eo
p
t
i
mi
z
a
r
e
su
nb
e
n
e
f
i
c
i
oq
u
el
l
a
ma
mo
sB
(
X
,
Y
)
l
o
sc
o
mp
u
t
a
d
o
r
at
i
e
n
eu
nb
e
n
e
f
i
c
i
od
et
i
p
oAt
i
e
n
eu
nb
e
n
e
f
i
c
i
od
e6
0
$y
l
l
a
ma
r
e
mo
sXa
e
s
t
en
u
me
r
od
ec
o
mp
u
t
a
d
o
r
a
,
e
l
b
e
n
e
f
i
c
i
os
e
r
ád
e6
0
& p
o
r
e
l
n
u
me
r
od
ec
o
mp
u
t
a
d
o
r
a
v
e
n
d
i
d
oma
s
e
l
b
e
n
e
f
i
c
i
oq
u
e
a
p
o
r
t
a
l
o
s
c
o
mp
u
t
a
d
o
r
a
oBq
u
e
e
ne
s
t
e
c
a
s
oe
s
5
5
$
B
(
x
,
y
)
=6
0
x
+
5
5
y
e
s
t
a
e
s
n
u
e
s
t
r
af
u
n
c
i
ó
n
o
b
j
e
t
i
v
o
.
P
l
a
n
t
e
a
r
e
mo
sn
u
e
s
t
r
o s
i
s
t
e
ma d
e e
c
u
a
c
i
ó
n yt
e
n
e
mo
sq
u
e p
a
r
a u
n
o c
o
mp
u
t
a
d
o
r
a
t
e
n
e
mo
su
n
a
sh
r
s
.q
u
en
e
c
e
s
i
t
a
mo
se
nma
q
u
i
n
ayt
e
n
e
mo
s2
x
+
3
yt
e
n
e
mo
sc
o
mo
má
x
i
mo
s3
0
0h
o
r
a
sme
n
o
r
ei
g
u
a
l
3
0
0h
o
r
a
syt
r
a
b
a
j
oama
n
ot
e
n
e
mo
s½h
o
r
ap
a
r
al
o
s
e
q
u
i
p
o
sA+
¼ d
eh
o
r
a
sp
a
r
al
o
se
q
u
i
p
o
sBy
t
e
n
e
mo
su
nmá
x
i
mod
e6
0h
o
r
a
s
,
½x+¼y
_6
0
y
e
n
t
r
e
a
mb
o
s
c
o
mp
u
t
a
d
o
r
a
t
e
n
e
mo
s
q
u
e
p
r
o
d
u
c
i
r
c
o
momí
n
i
mo9
0e
n
t
o
c
e
s
x
+
y /9
0 t
a
mb
i
é
np
l
a
n
t
e
a
r
e
mo
sd
o
sc
o
n
d
i
c
i
o
n
e
se
l
n
u
me
r
od
ec
o
mp
u
t
a
d
o
r
ad
e
b
ed
e
s
e
r
s
i
e
mp
r
e
ma
y
oq
u
e
0
x /0
y /0
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
C
o
me
n
z
a
mo
sar
e
p
r
e
s
e
n
t
a
r
g
r
á
f
i
c
a
me
n
t
ea 2
x+3
y= 3
0
0 yt
o
ma
mo
su
np
u
n
t
oe
ne
l
B
(
x
,
y
)
=6
0
x
+5
5
y
2
x
+
3
y
_ 3
0
0
½x
+¼y _6
0
x
+y /9
0
x /0
y /0
y
a
t
e
n
i
e
n
d
on
u
e
s
t
r
os
i
s
t
e
ma
d
e
i
n
e
c
u
a
c
i
ó
ny
r
e
s
o
l
v
e
mo
s
q
u
e
c
a
d
a
u
n
a
e
s
e
s
t
a
s
i
n
e
c
u
a
c
i
o
n
e
s
r
e
p
r
e
s
e
n
t
a
s
i
n
e
l
me
n
o
r
oi
g
u
a
l
u
n
a
e
c
u
a
c
i
ó
nd
e
u
n
a
l
í
n
e
a
r
e
c
t
a

4. p
l
a
n
oc
a
r
t
e
s
i
a
n
oc
o
moe
l
(
0
,
0
)
s
o
mb
r
e
a
mo
se
s
t
es
e
mi
p
l
a
n
oe
nd
o
n
d
es
ee
n
c
u
e
n
t
r
ae
l
p
u
n
t
o(
0
,
0
)
R
e
p
r
e
s
e
n
t
a
n
d
o½x
+¼y_6
0y
t
o
ma
mo
s
u
np
u
n
t
oe
ne
l
p
l
a
n
oc
a
r
t
e
s
i
a
n
oc
o
moe
l
(
0
,
0
)
y
n
o
sd
aq
u
e0e
sme
n
o
r
q
u
e3
0
0s
o
mb
r
e
a
mo
se
s
t
es
e
mi
p
l
a
n
oe
nd
o
n
d
es
ee
n
c
u
e
n
t
r
ae
l
p
u
n
t
o(
0
,
0
)
R
e
p
r
e
s
e
n
t
a
mo
sx+y= 9
0yt
o
ma
mo
su
np
u
n
t
oe
ne
l
p
l
a
n
oc
a
r
t
e
s
i
a
n
oc
o
moe
l
(
0
,
0
)
t
o
ma
n
d
oe
nc
u
e
n
t
aq
u
ee
l
0n
oe
sma
y
oq
u
e9
0s
o
mb
r
e
a
mo
sl
ao
t
r
ap
a
r
t
ed
e
l
s
e
mi
p
l
a
n
o
a
l
c
u
a
l
n
op
e
r
t
e
n
e
c
e
e
l
p
u
n
t
o(
0
,
0
)
Y
aq
u
e x /0 y y /0 s
e
e
n
c
u
e
n
t
r
a
ne
ne
l
p
r
i
me
r
c
u
a
d
r
a
n
t
e
y
t
e
n
e
mo
s
e
n
t
o
n
c
e
a
s
í
n
u
e
s
t
r
op
o
l
í
g
o
n
oon
u
e
s
t
r
a
r
e
g
i
of
a
c
t
i
b
l
e
Y
a
t
e
n
i
e
n
d
on
u
e
s
t
r
a
r
e
g
i
ó
nf
a
c
t
i
b
l
e
d
e
b
e
mo
s
h
a
l
l
a
l
o
s
v
é
r
t
i
c
e
s
d
e
e
s
a
r
e
g
i
ó
n
R
e
s
o
l
v
i
e
n
d
o s
i
s
t
e
ma d
e d
o
s e
c
u
a
c
i
o
n
e
s c
o
n d
o
s i
n
c
ó
g
n
i
t
a
s y
a q
u
e t
e
n
e
mo
s t
r
e
s
e
c
u
a
c
i
o
n
e
s
d
e
r
e
c
t
a
s
d
i
f
e
r
e
n
t
e
s
c
a
n
t
i
d
a
d
e
s
R
e
s
o
l
v
e
mo
s
c
o
nl
o
s
c
o
r
t
e
s
d
e
l
o
s
e
j
e
s
Xy
e
l
e
j
e
Yc
o
nl
o
s
s
i
g
u
i
e
n
t
e
s
v
é
r
t
i
c
e
s
B
(
x
,
y
)
=6
0
x
+5
5
y
B(
0
.
9
0
)
=
4
9
5
0$
B(
0
,
1
0
0
)
=
5
5
0
0$
B(
9
0
,
0
)
=
5
4
0
0$
B(
1
2
0
,
0
)
=
7
2
0
0$
B(
1
0
5
,
3
0
)
=
7
9
5
0$
N
o
s
p
e
d
í
a
a
q
u
e
l
l
ol
a
c
a
n
t
i
d
a
dd
e
c
o
mp
u
t
a
d
o
r
a
d
e
c
a
d
a
t
i
p
oh
a
d
e
p
r
o
d
u
c
i
r
s
e
p
a
r
a
b
e
n
e
f
i
c
i
os
e
a
má
x
i
moy
l
a
r
e
s
p
u
e
s
t
a
B(
1
0
5
,
3
0
)
=7
9
5
0$e
s
q
u
e
d
e
b
e
mo
s
f
a
b
r
i
c
a
r
1
0
5
c
o
mp
u
t
a
d
o
r
a
t
i
p
oA y
3
0c
o
mp
u
t
a
d
o
r
a
t
i
p
oBp
a
r
a
q
u
e
e
l
b
e
n
e
f
i
c
i
os
e
a
má
x
i
moc
o
nd
i
c
h
o
b
e
n
e
f
i
c
i
oa
7
9
5
0$