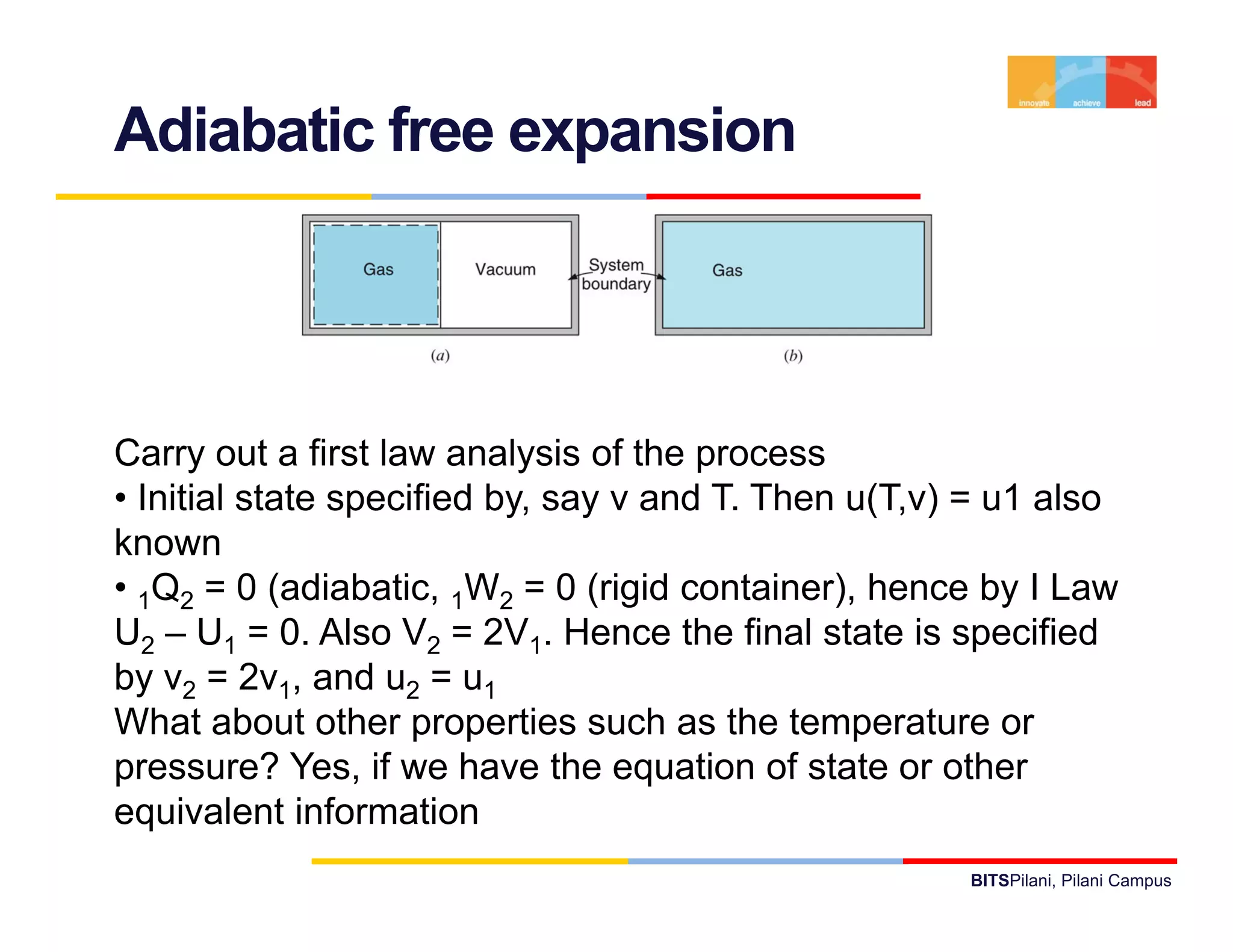
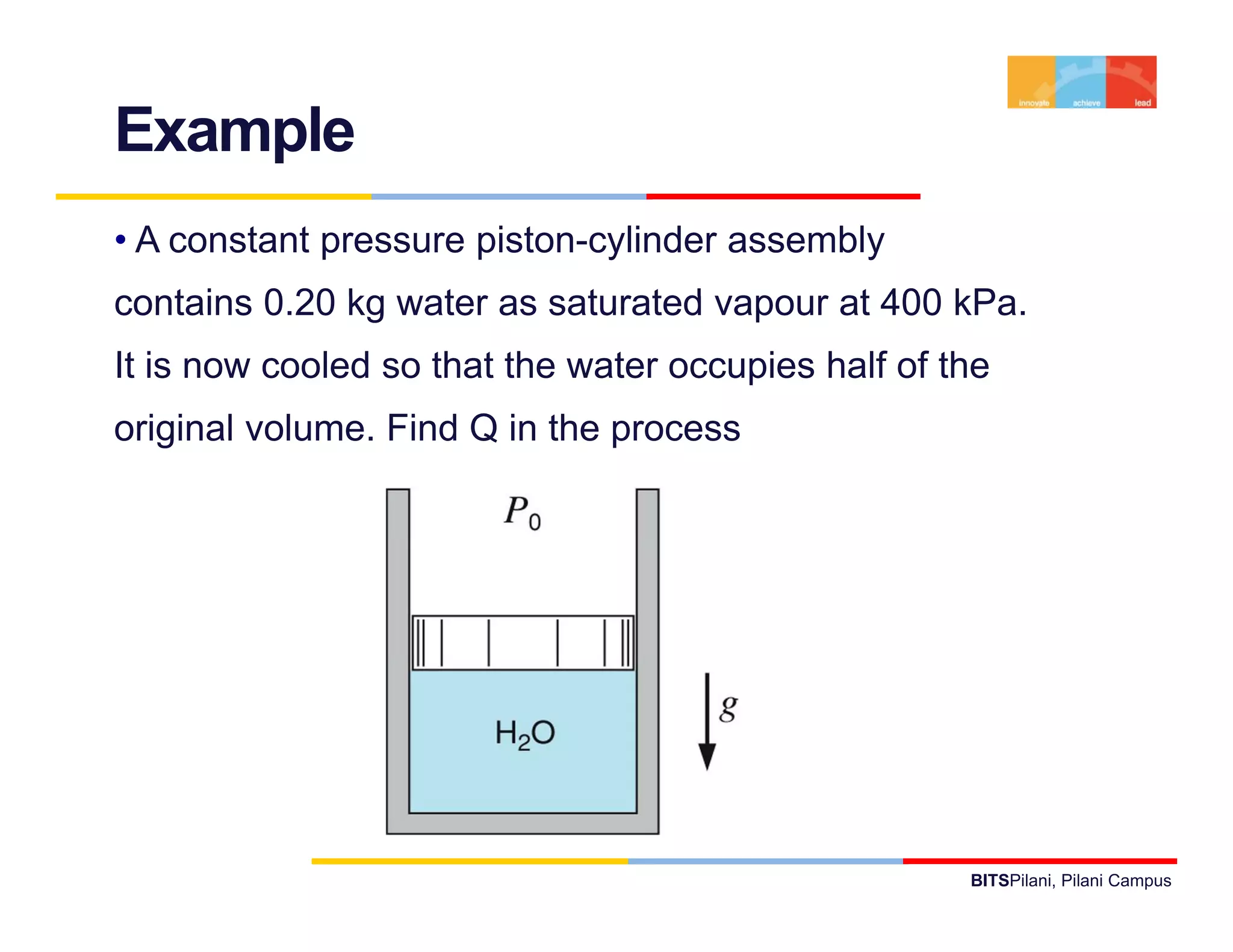
- The document discusses the first law of thermodynamics as it applies to control masses.
- It defines important thermodynamic concepts like internal energy, enthalpy, specific heat, and introduces the use of tables of thermodynamic properties.
- It provides examples of applying the first law to processes involving ideal gases and liquids/solids, calculating work, heat, internal energy and enthalpy changes.