Ken Plummer, profile picture
Uploaded byKen Plummer
PPTX, PDF5,951 views

The nature of the data

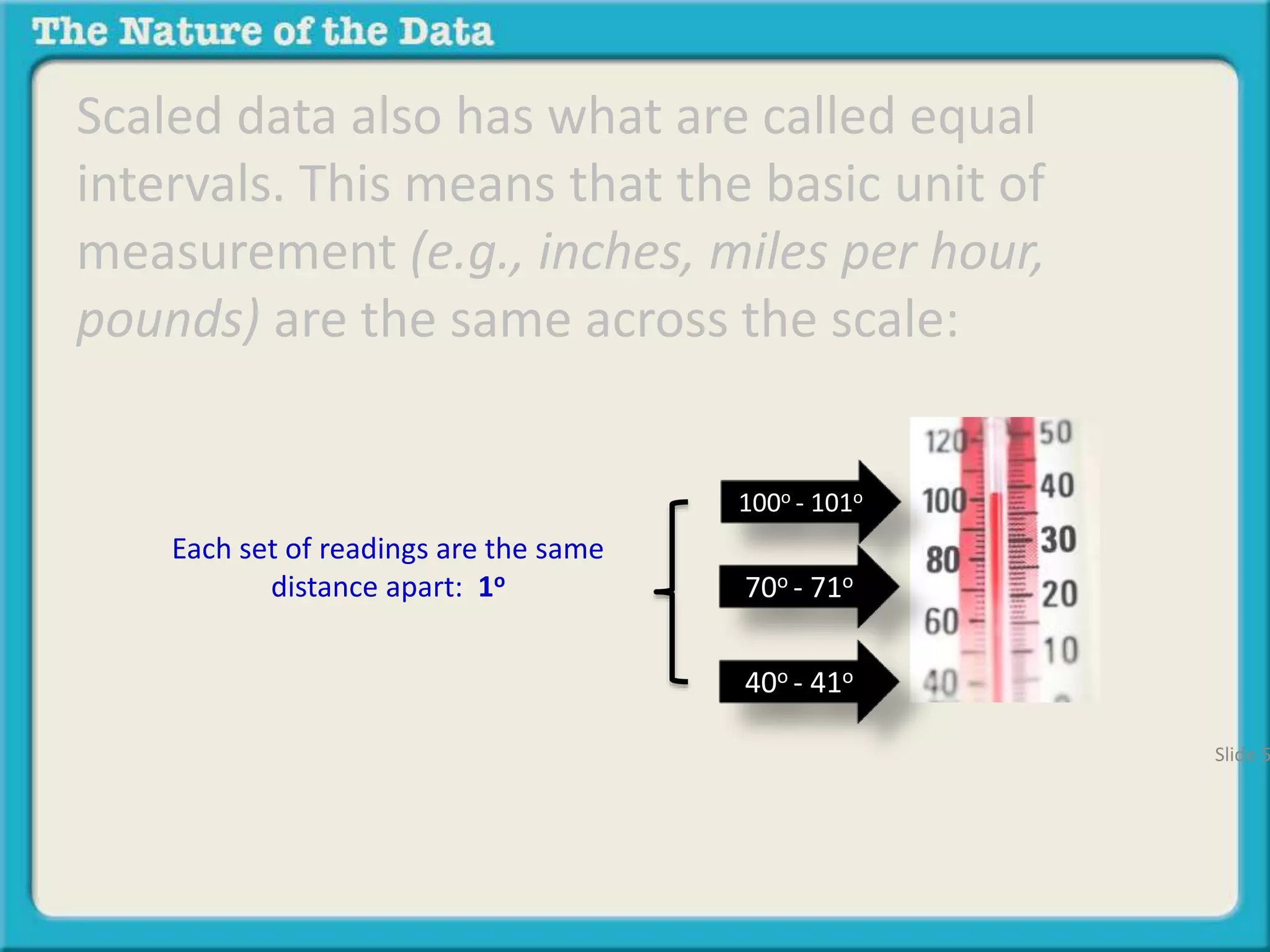
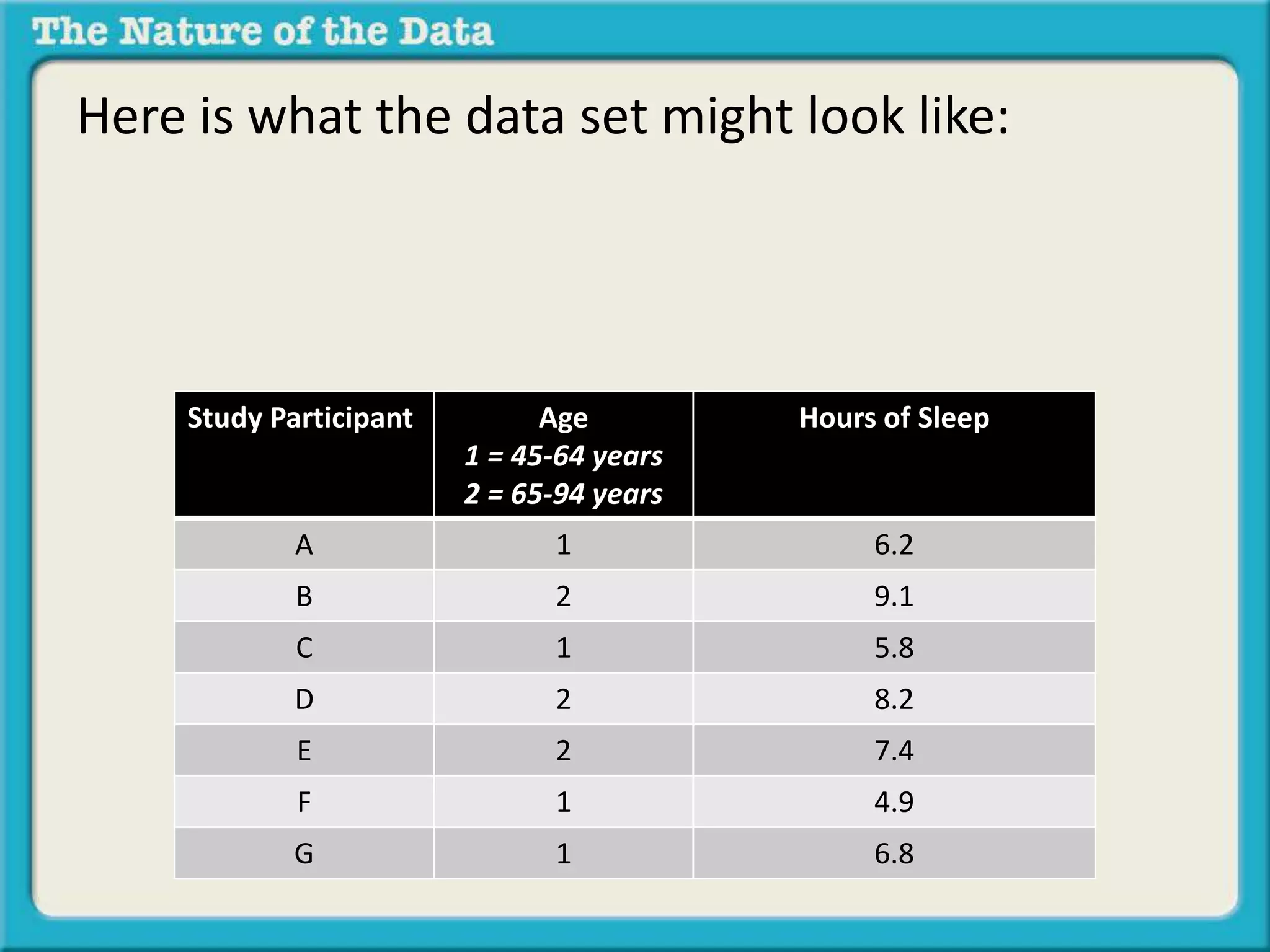
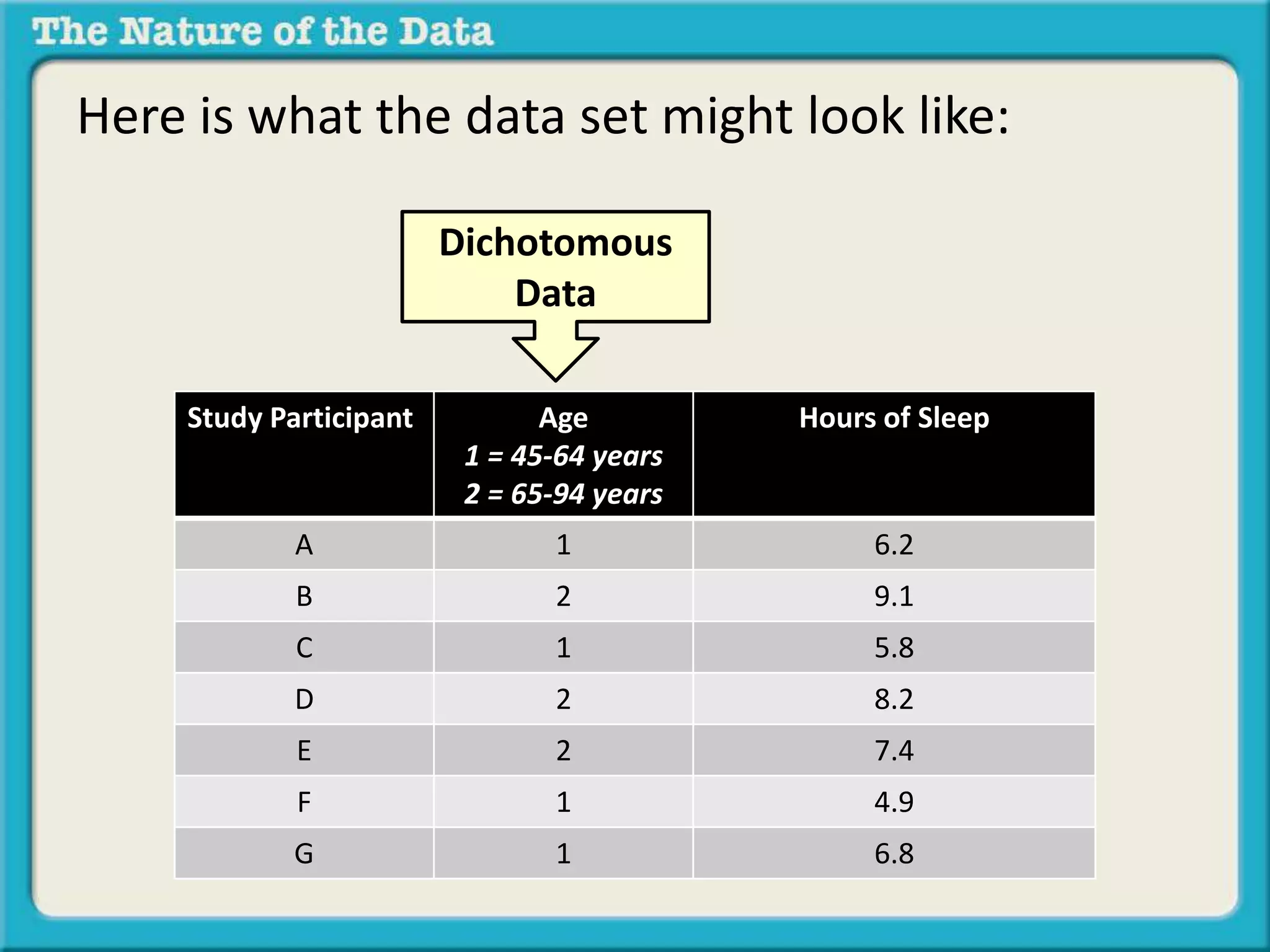
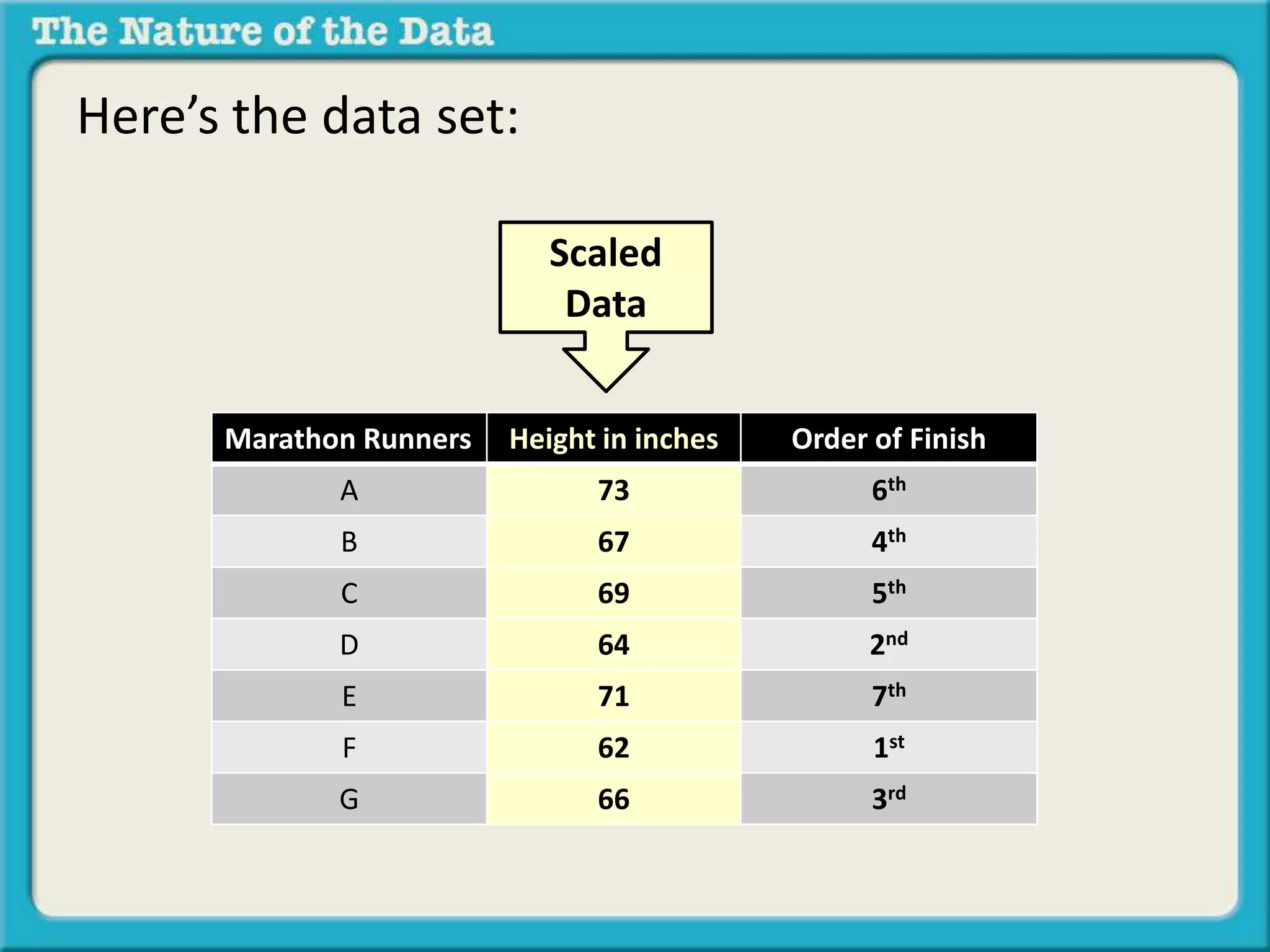
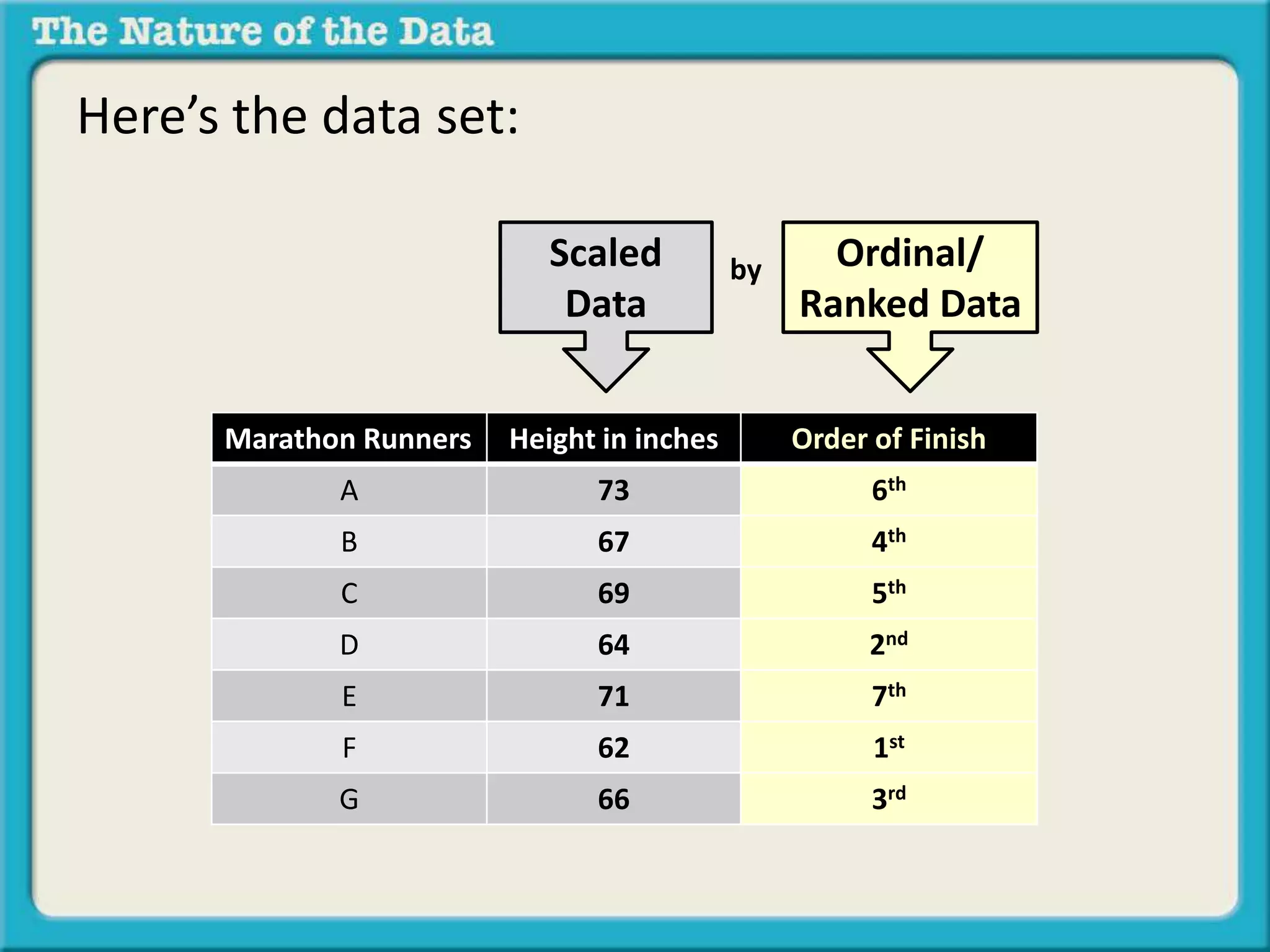
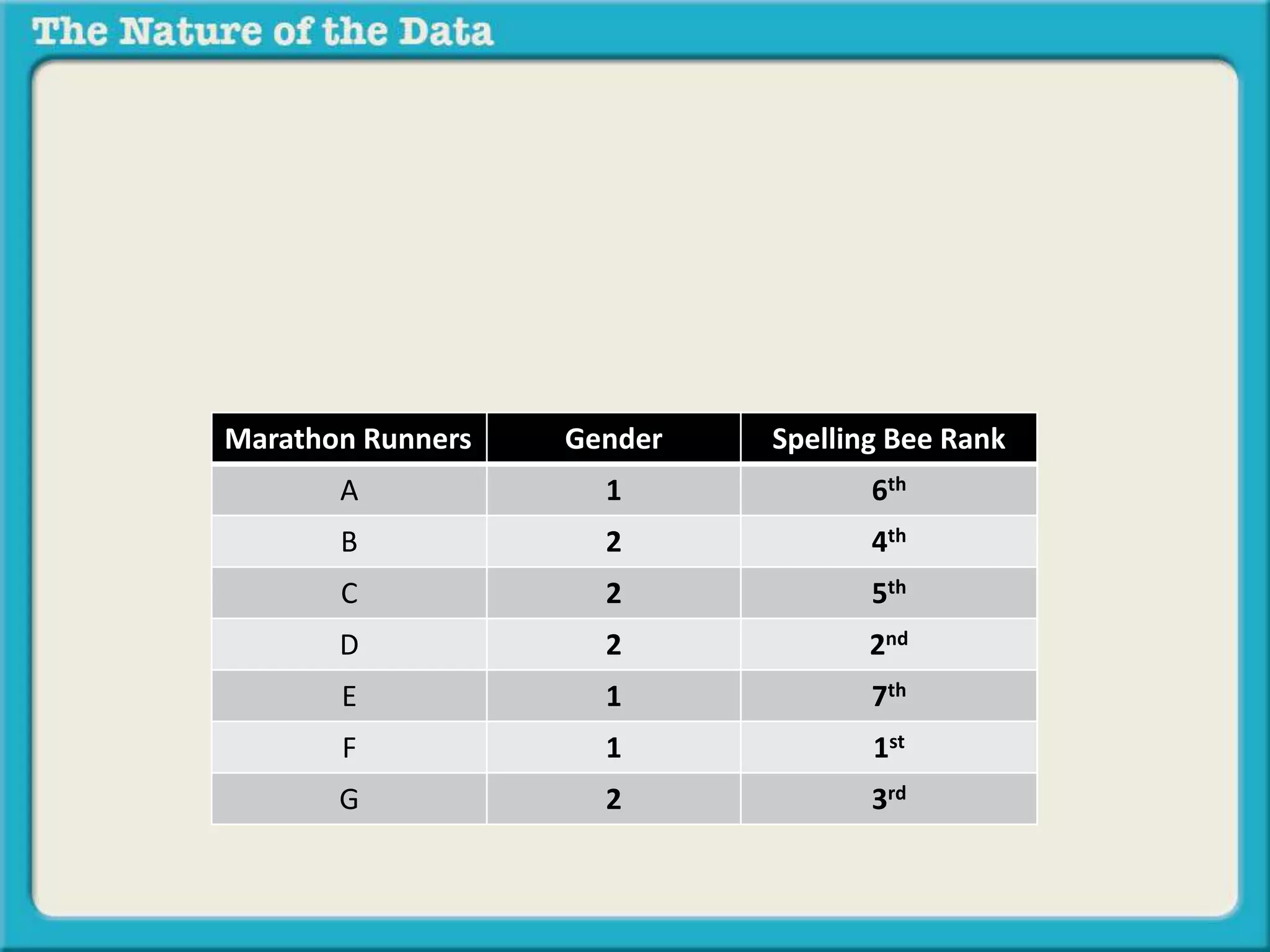
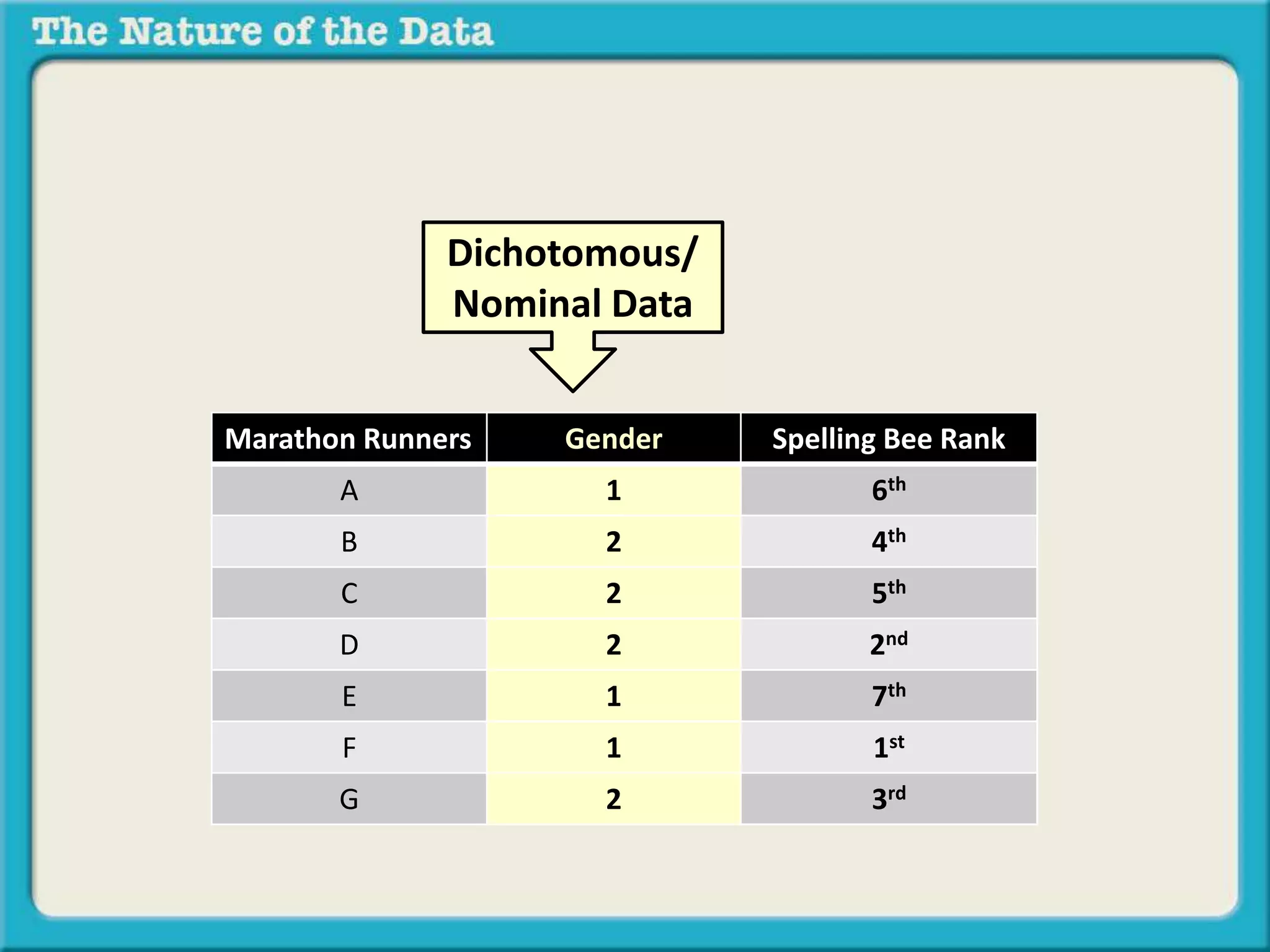
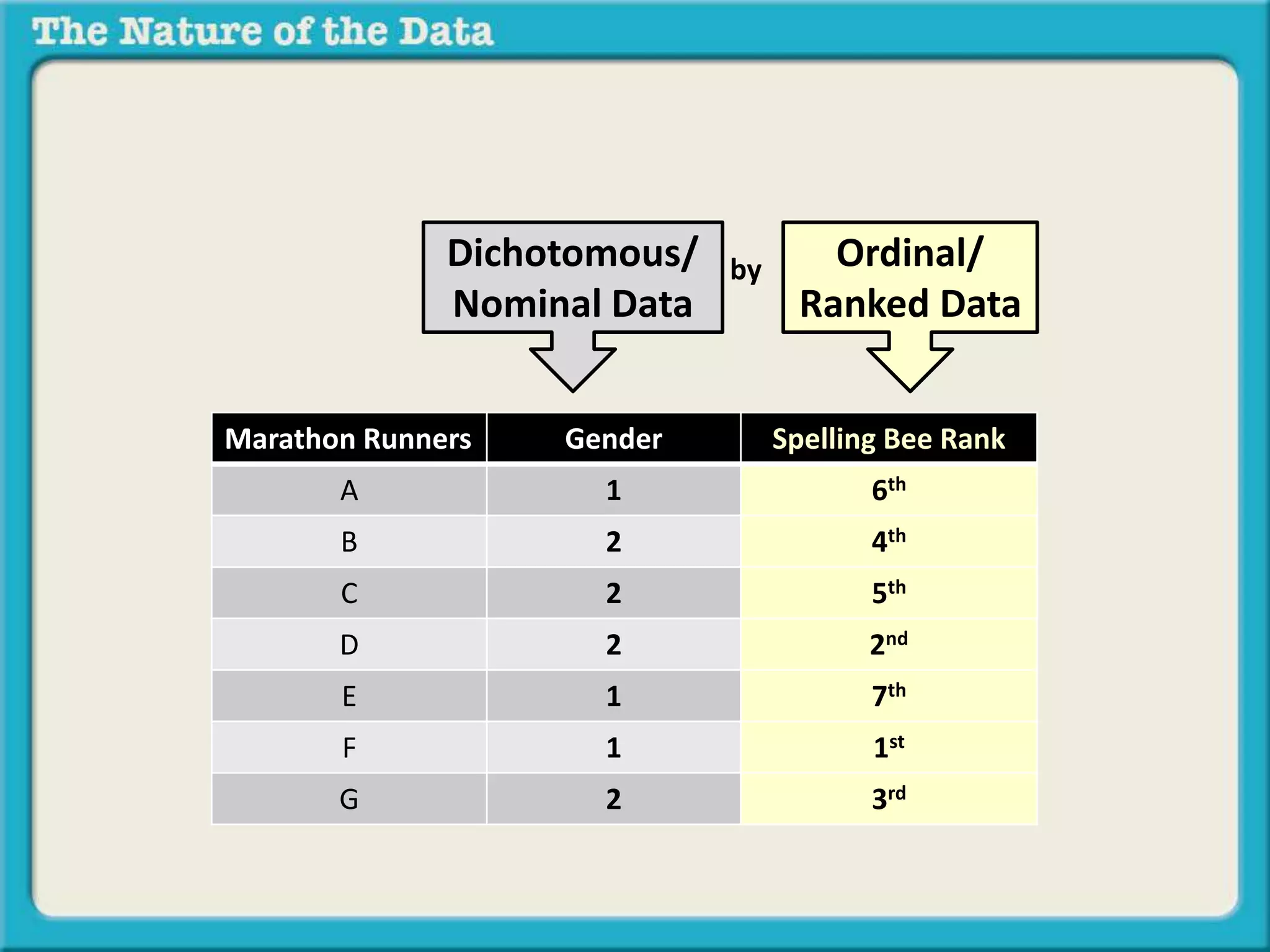
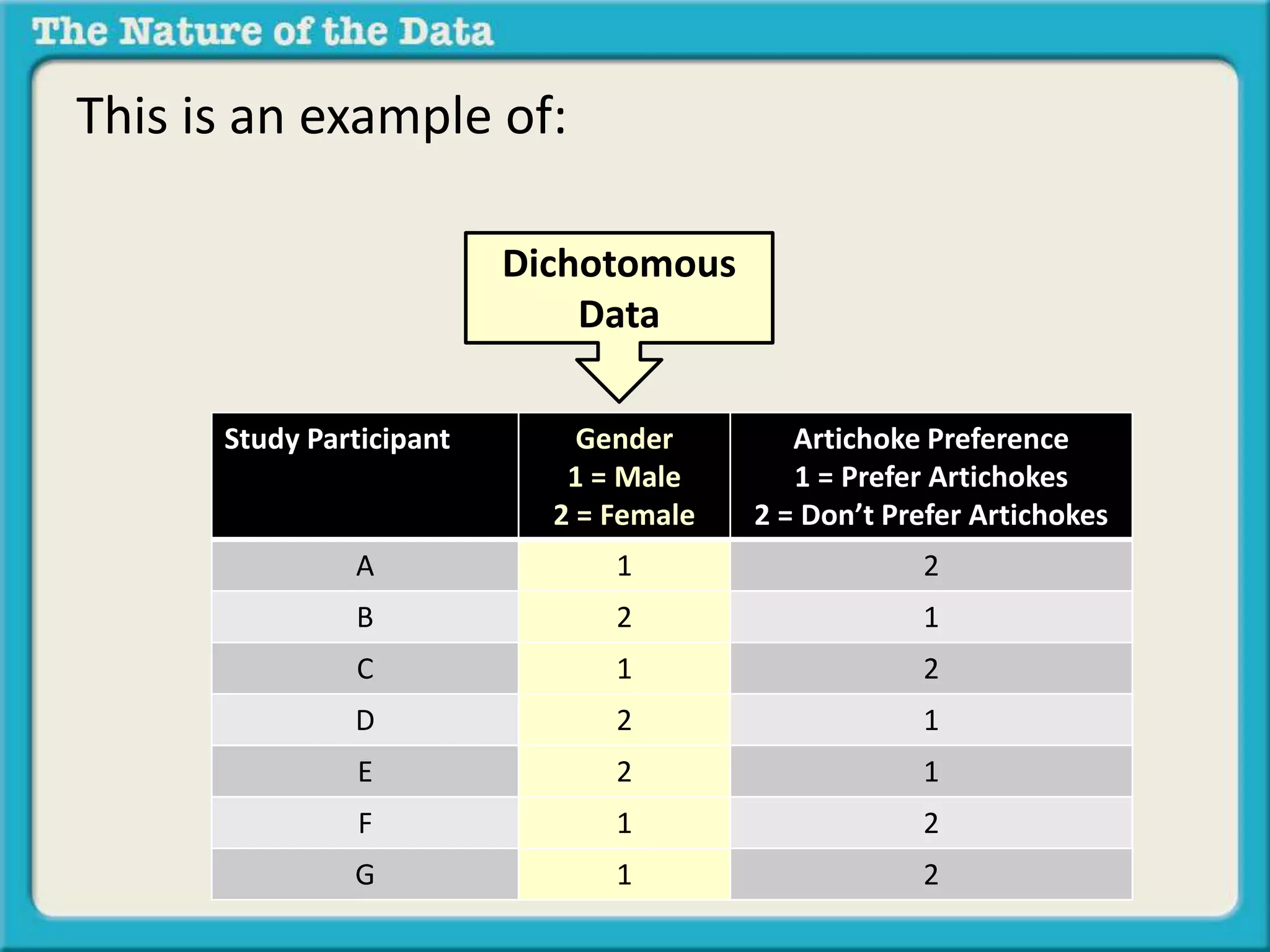
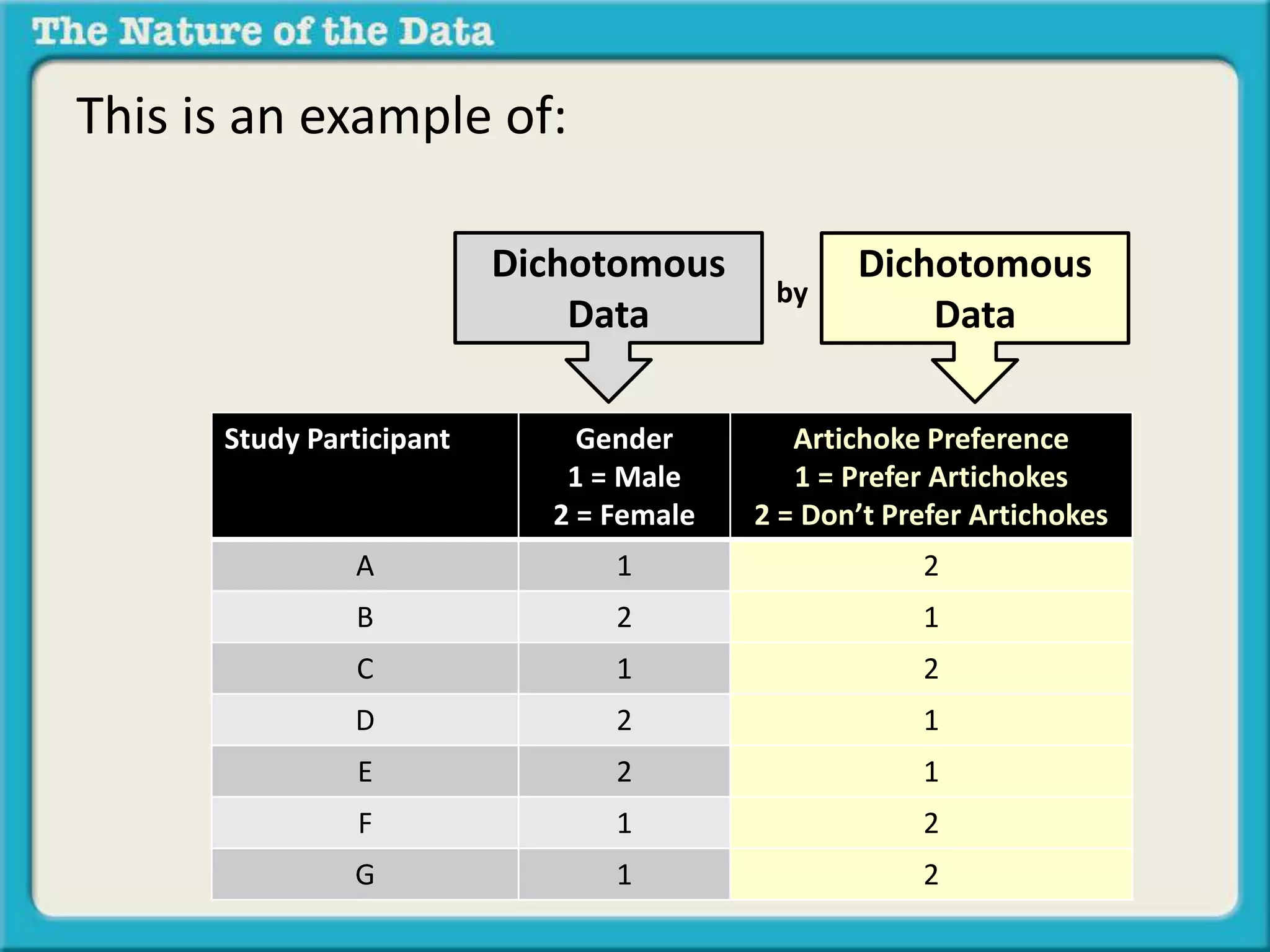
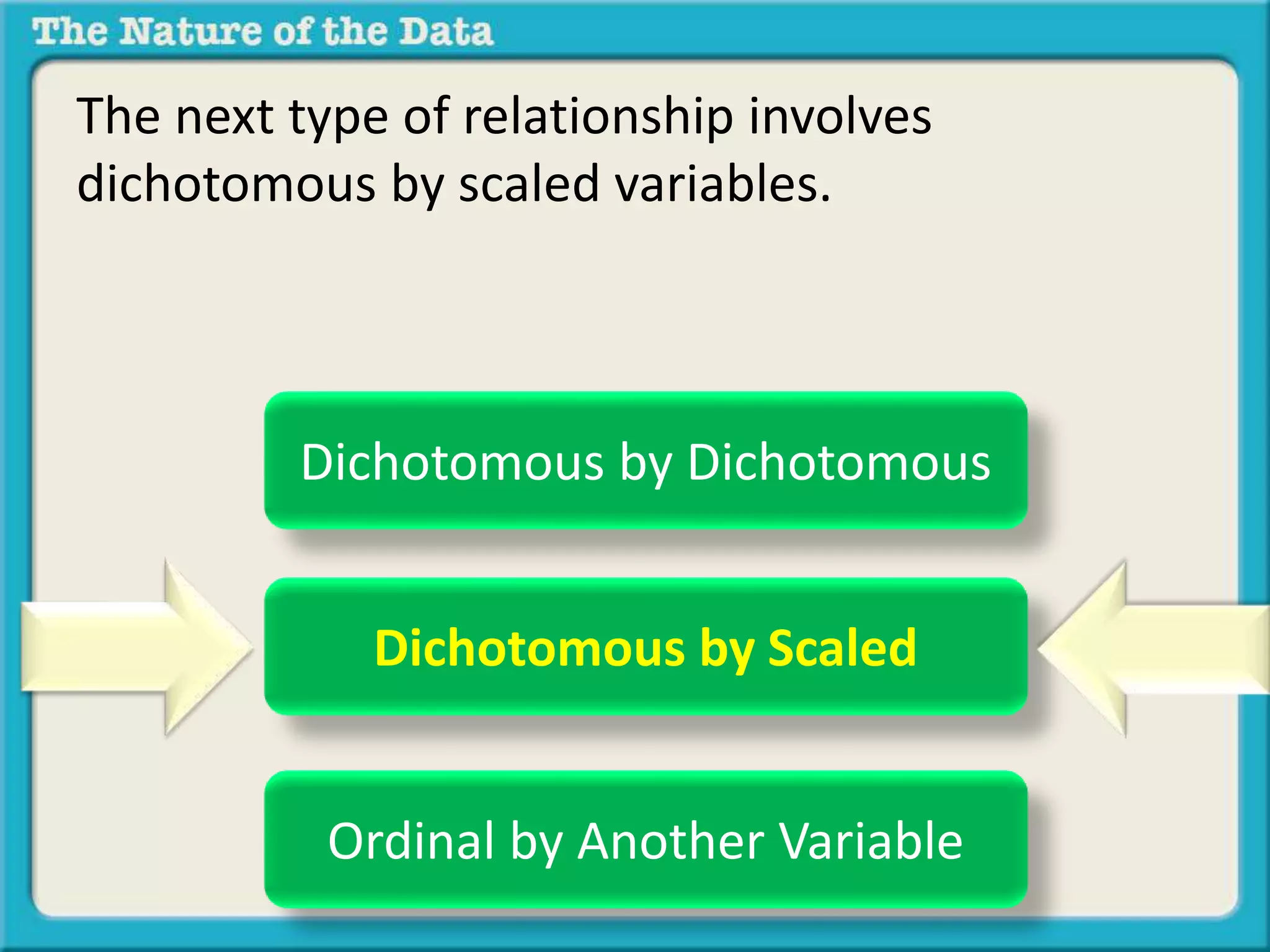
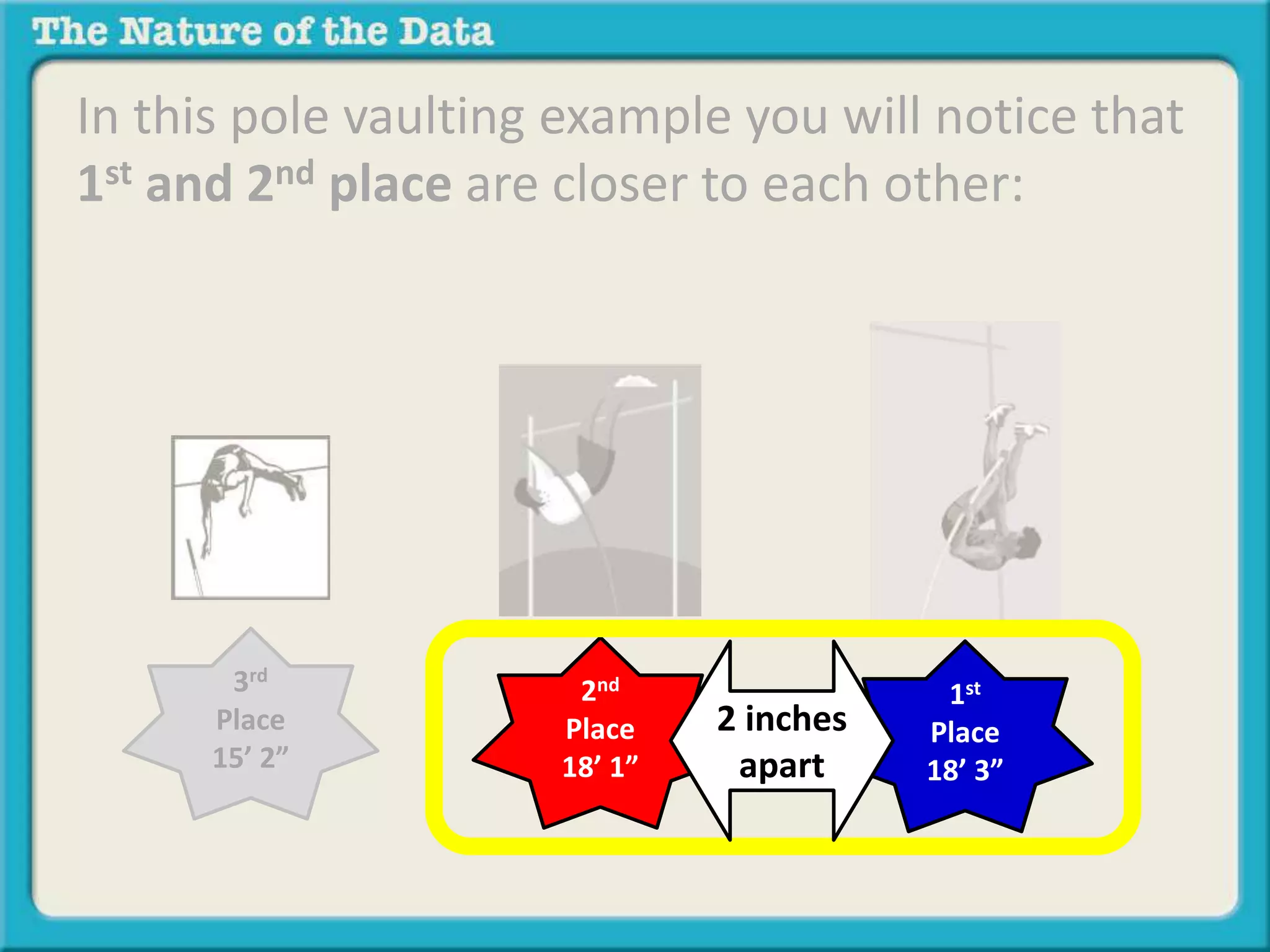
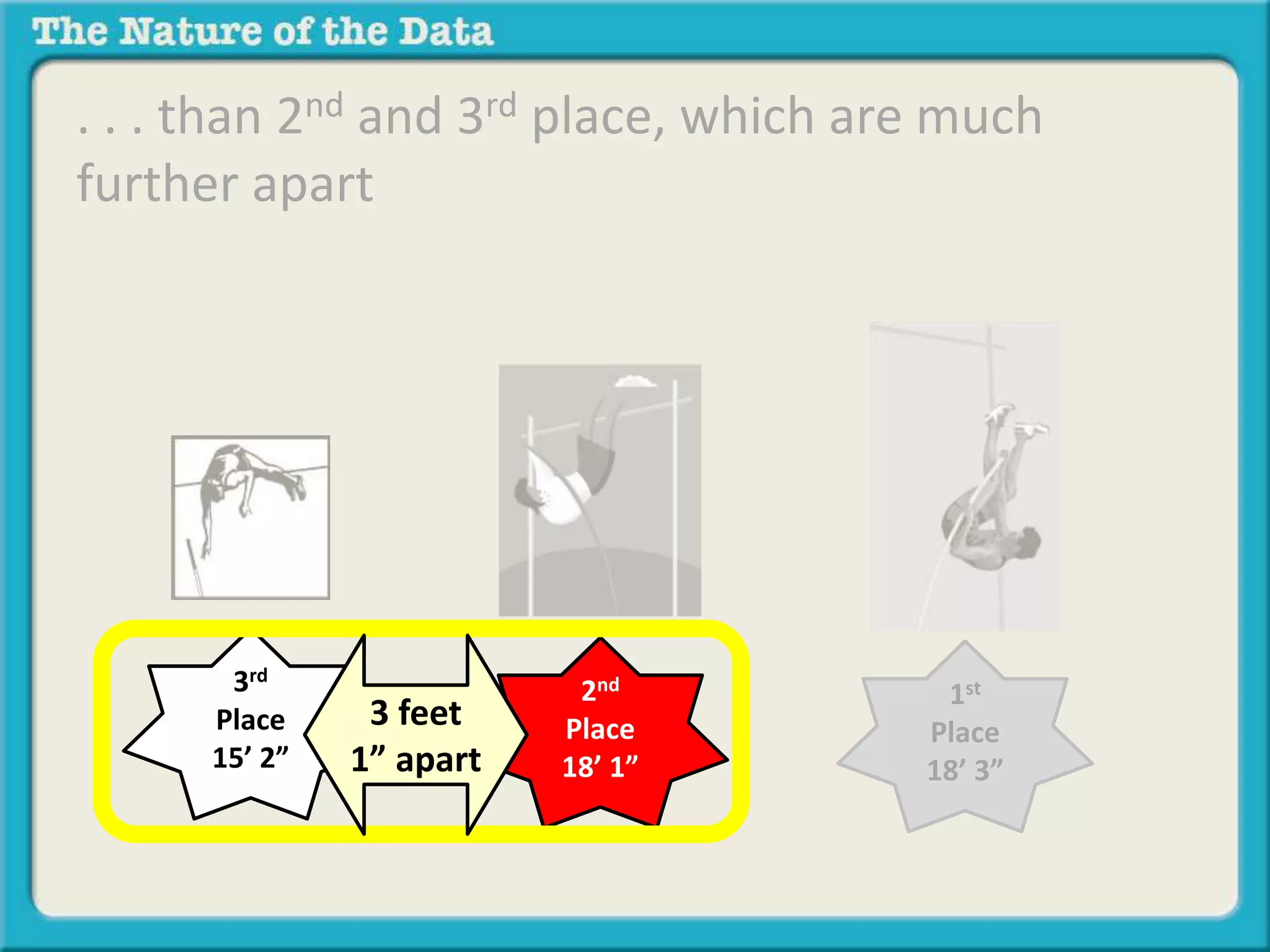
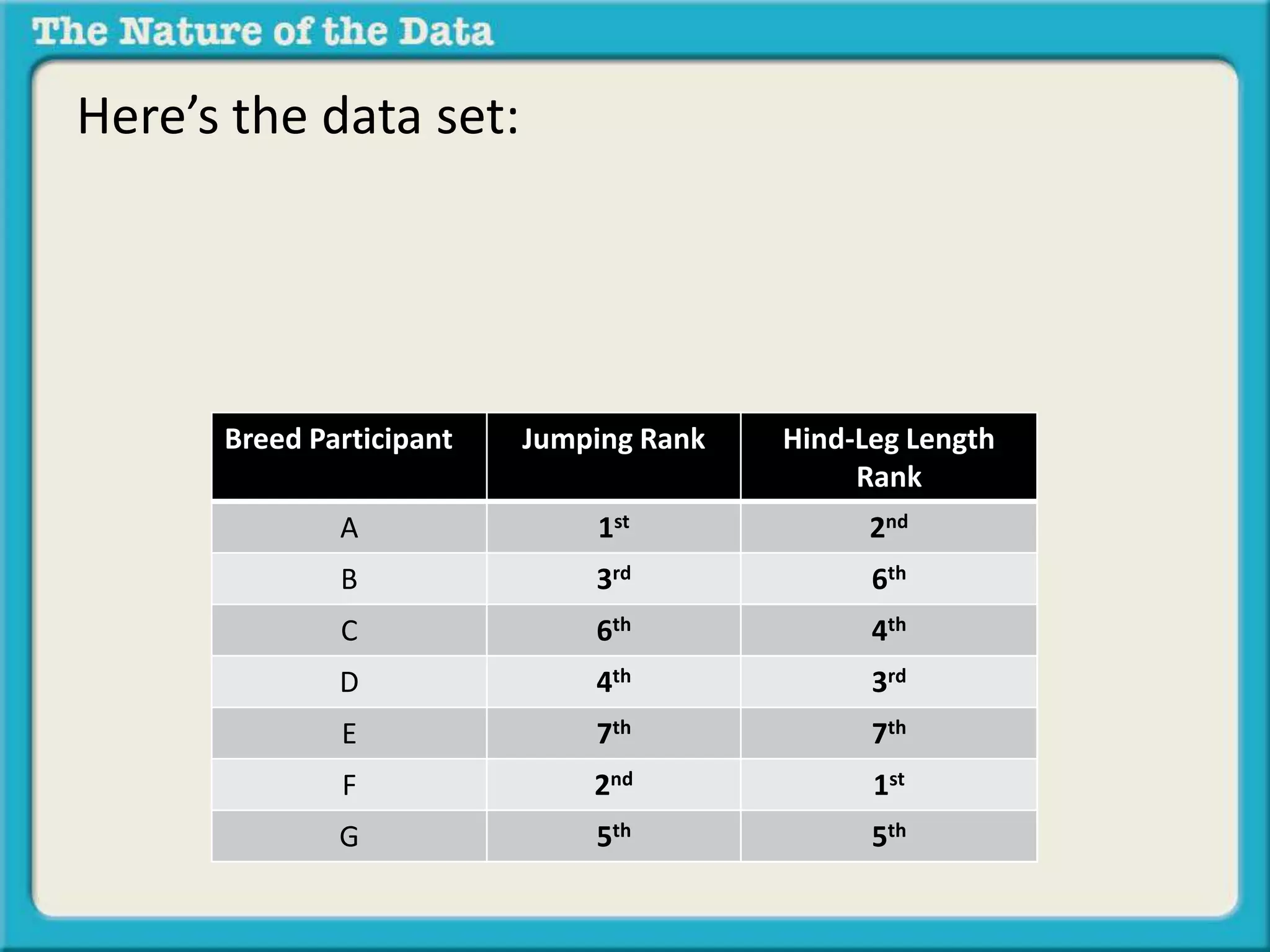
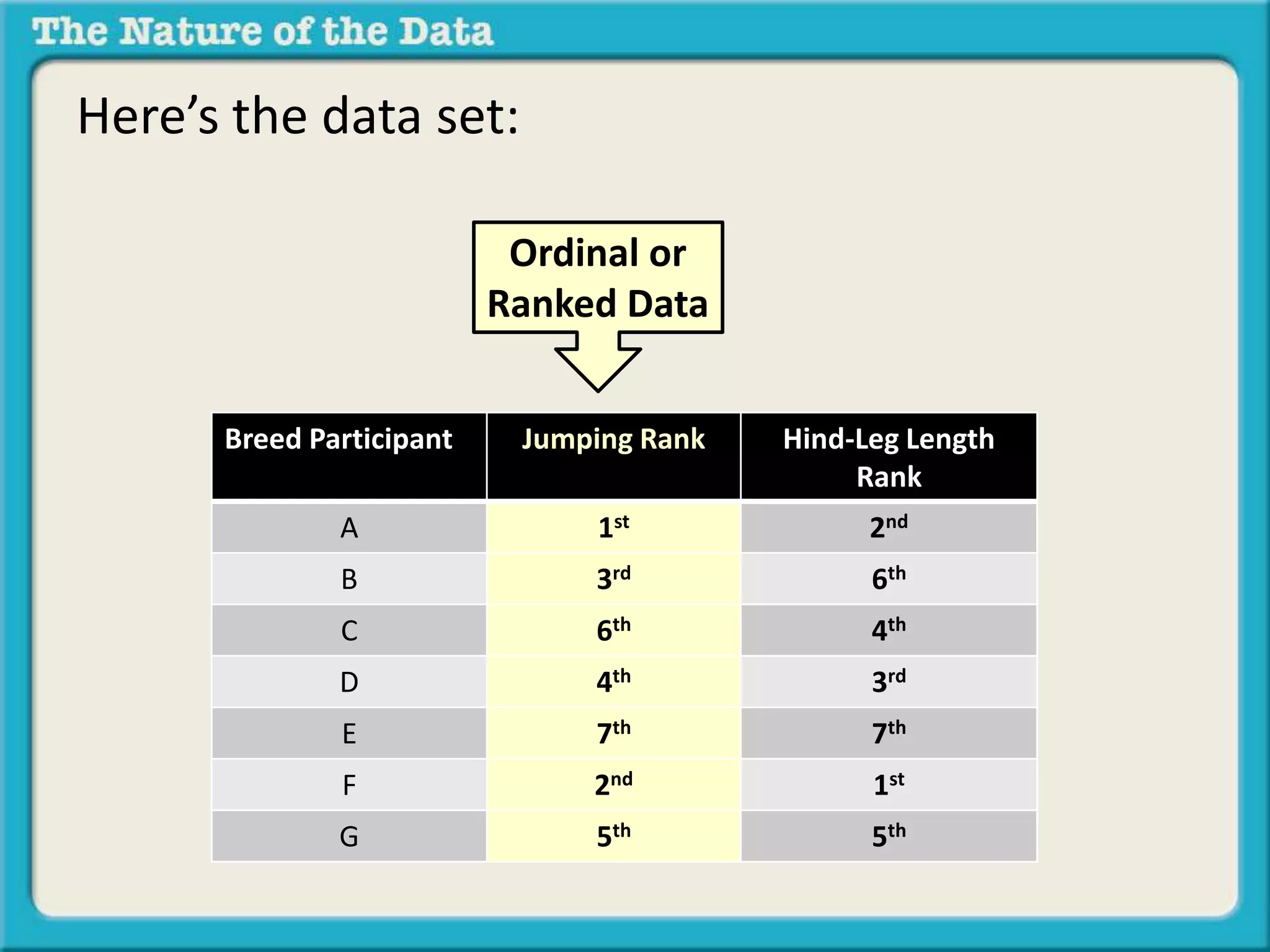
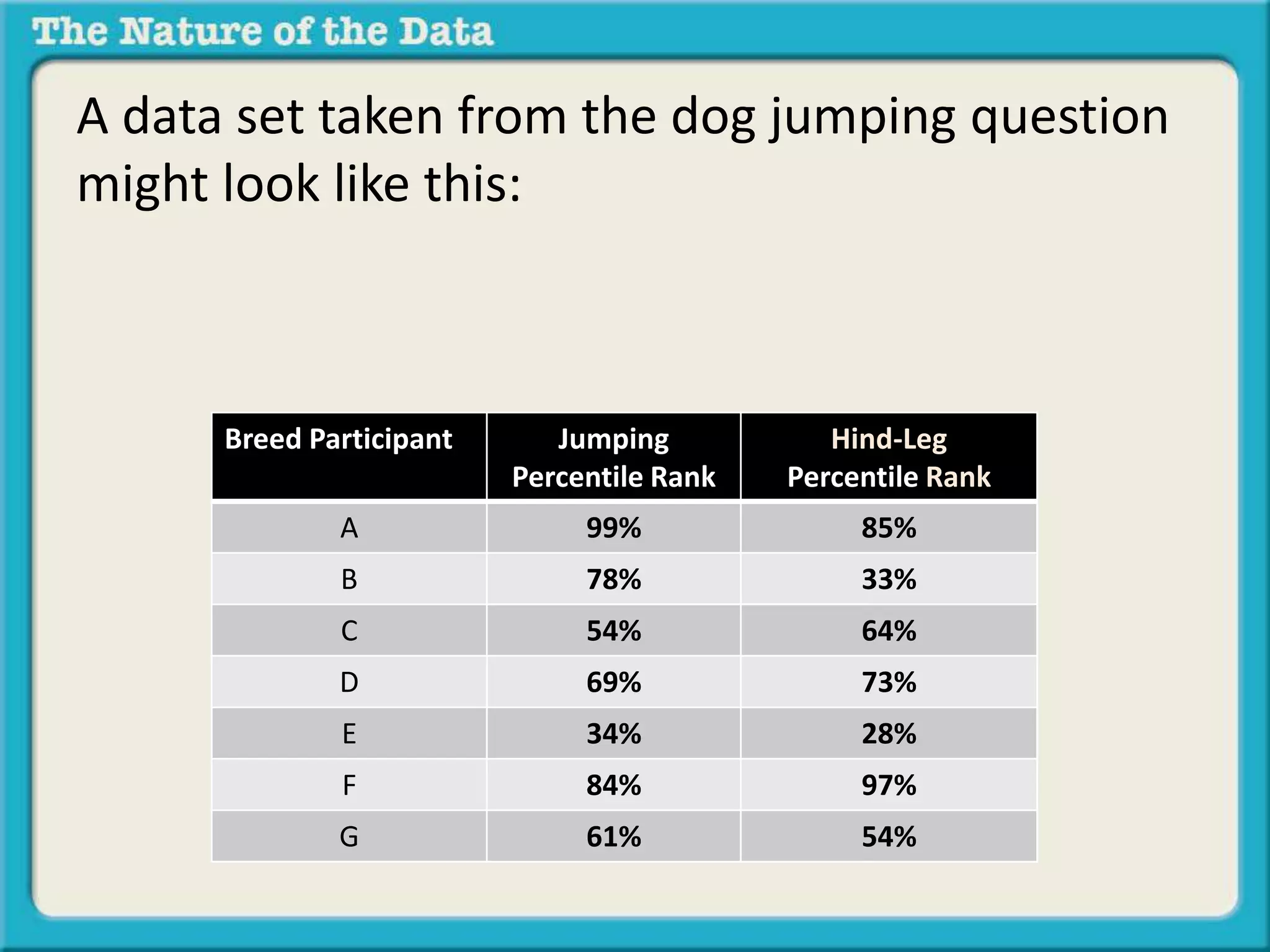
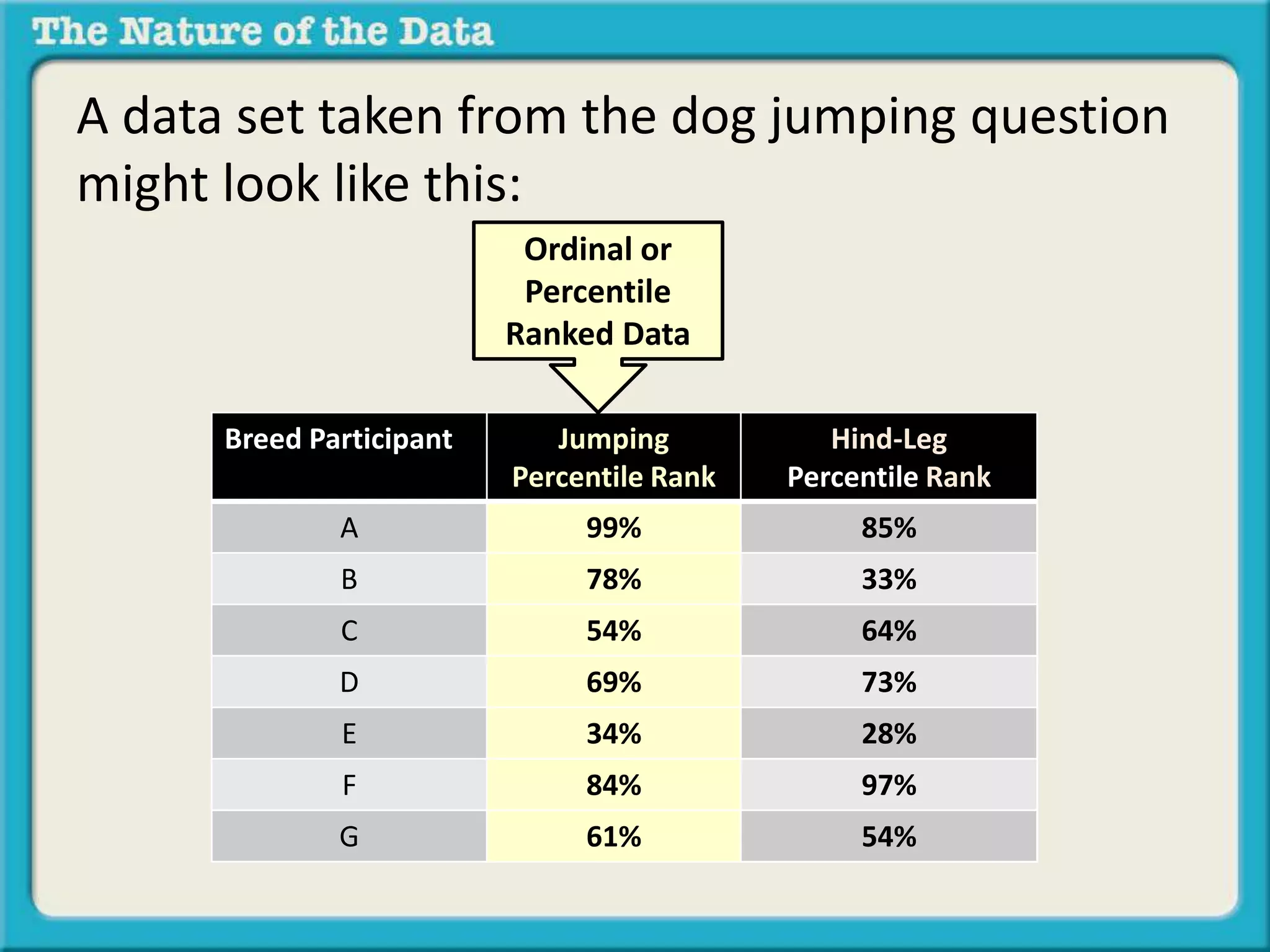
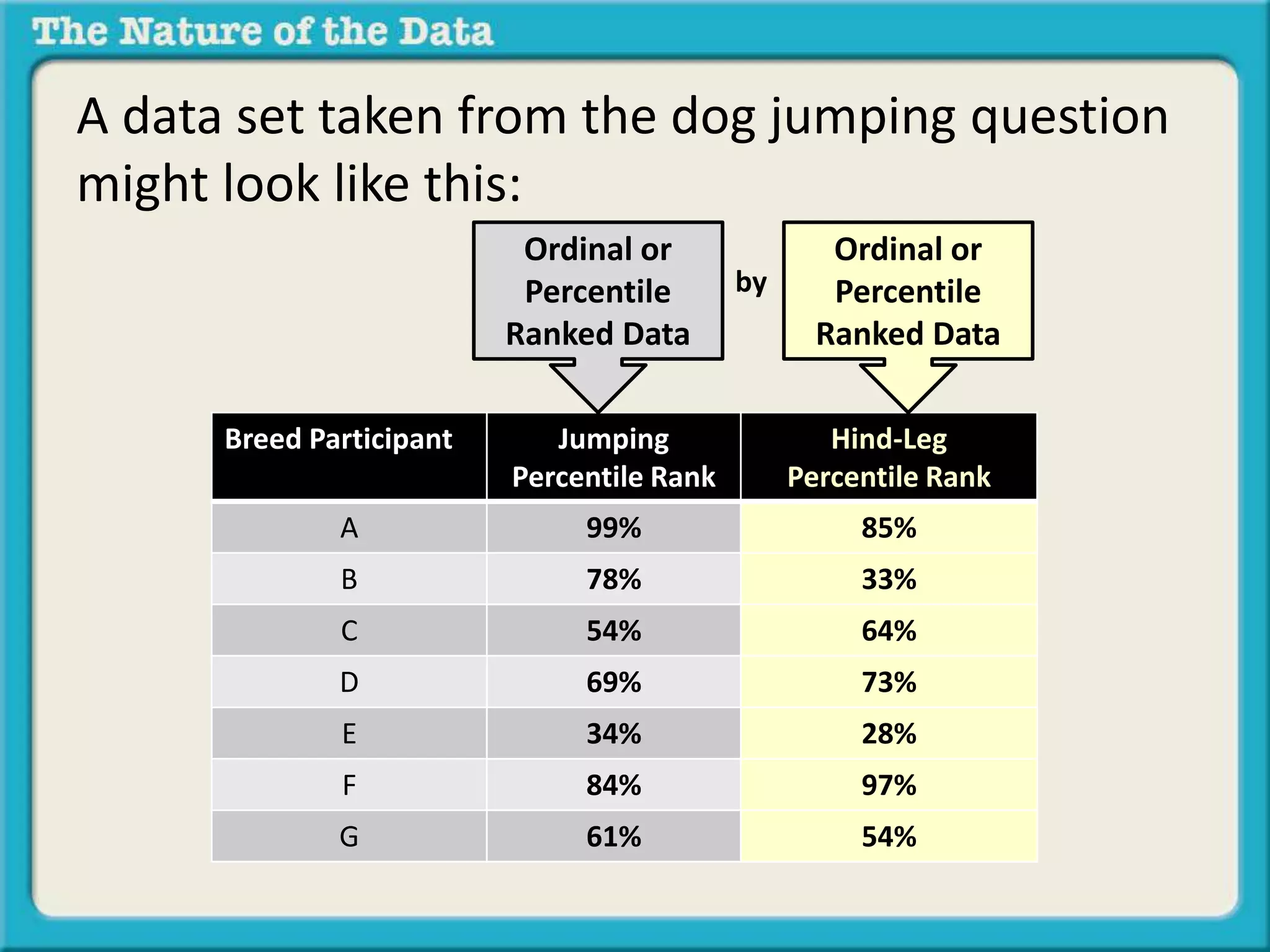
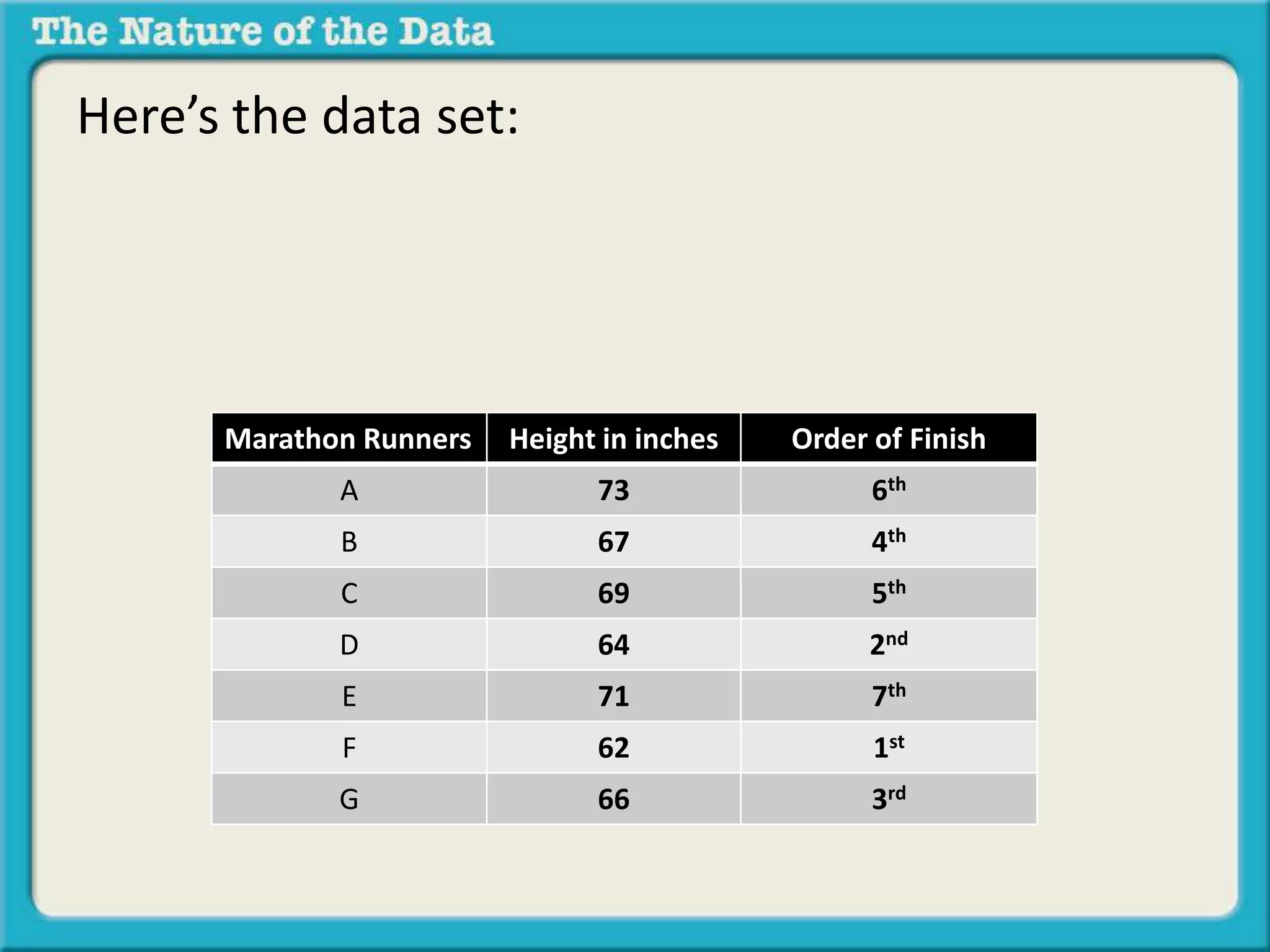
The document discusses different types of relationships between variables in data sets: - Dichotomous by dichotomous data examines the relationship between two variables that can only take two values each, like gender and artichoke preference. - Dichotomous by scaled data looks at the relationship between a dichotomous variable and a scaled variable, such as age group and hours of sleep. - Ordinal by another variable considers the relationship when one variable ranks items but the intervals between ranks are unequal, like pole vaulting placements.

Embed presentation

Downloaded 50 times
1 / 123
2 / 123
Most read
3 / 123
4 / 123
5 / 123
6 / 123
7 / 123
8 / 123
9 / 123
10 / 123
11 / 123
12 / 123
13 / 123
14 / 123
15 / 123
16 / 123
17 / 123
18 / 123
19 / 123
20 / 123
Most read
21 / 123
22 / 123
23 / 123
24 / 123
25 / 123
26 / 123
27 / 123
28 / 123
29 / 123
30 / 123
31 / 123
32 / 123
33 / 123
34 / 123
35 / 123
36 / 123
37 / 123
38 / 123
39 / 123
40 / 123
41 / 123
42 / 123
43 / 123
44 / 123
45 / 123
46 / 123
47 / 123
48 / 123
49 / 123
50 / 123
51 / 123
52 / 123
53 / 123
54 / 123
55 / 123
56 / 123
57 / 123
58 / 123
59 / 123
60 / 123
61 / 123
62 / 123
63 / 123
64 / 123
65 / 123
66 / 123
67 / 123
68 / 123
69 / 123
70 / 123
71 / 123
72 / 123
73 / 123
74 / 123
75 / 123
76 / 123
77 / 123
78 / 123
79 / 123
80 / 123
81 / 123
82 / 123
83 / 123
84 / 123
85 / 123
86 / 123
87 / 123
88 / 123
89 / 123
90 / 123
91 / 123
92 / 123
93 / 123
94 / 123
95 / 123
96 / 123
97 / 123
98 / 123
99 / 123
100 / 123
101 / 123
102 / 123
103 / 123
104 / 123
105 / 123
106 / 123
107 / 123
108 / 123
109 / 123
110 / 123
111 / 123
112 / 123
113 / 123
114 / 123
115 / 123
116 / 123
117 / 123
118 / 123
119 / 123
120 / 123
121 / 123
122 / 123
123 / 123
The Nature of Your Data
The purpose of this presentation is to help you determine if the two data sets you are working with in this problem are:
The purpose of this presentation is to help you determine if the two data sets you are working with in this problem are: Dichotomous by Dichotomous Dichotomous by Scaled or Ordinal by Another Variable
First, let's define what each of these mean. Dichotomous by Dichotomous Dichotomous by Scaled or Ordinal by Ordinal
Beginning with Dichotomous by Dichotomous
What is dichotomous data?
The "Di" in Dichotomous means "two"
. . . and "tomous" or "tomy" as in “appendec-tomy” means to divide by.
. . . and "tomous" or "tomy" as in “appendec-tomy” means to divide by.
So, dichotomous means to divide by two.
In this case a variable is divided by two or specifically it can only take on two values.
For example:
Gender is a good example of a dichotomous data.
Gender is a good example of a dichotomous data. It generally takes on two values
Gender is a good example of a dichotomous data. It generally takes on two values (1) male (2) female
In some cases individuals are divided by (1) those who received a treatment and (2) those who did not.
For example:
You have been asked to determine if those who eat asparagus score higher on a well-being scale (1-10) than those who do not.
You have been asked to determine if those who eat asparagus score higher on a well-being scale (1-10) than those who do not.
You have been asked to determine if those who eat asparagus score higher on a well-being scale (1-10) than those who do not. In this case, we are dealing with those (1) who eat asparagus and those (2) who do not.
With dichotomous by dichotomous data you are examining the relationship between two dichotomous variables.
Here is an example:
It has been purported that females prefer artichokes more than do males.
It has been purported that females prefer artichokes more than do males.
It has been purported that females prefer artichokes more than do males. Dichotomous variable 1: Gender (1)Male (2)Female
It has been purported that females prefer artichokes more than do males. Dichotomous variable 1: Gender (1)Male (2)Female
It has been purported that females prefer artichokes more than do males. Dichotomous variable 1: Gender (1)Male (2)Female
It has been purported that females prefer artichokes more than do males. Dichotomous variable 2: Artichoke Preference (1)Prefer Artichokes (2)Do not prefer Artichokes
It has been purported that females prefer artichokes more than do males. Dichotomous variable 2: Artichoke Preference (1)Prefer Artichokes (2)Do not prefer Artichokes
It has been purported that females prefer artichokes more than do males. Dichotomous variable 2: Artichoke Preference (1)Prefer Artichokes (2)Do not prefer Artichokes
Here is what the data set looks like:
It has been purported that females prefer artichokes more than do males. Study Participant Gender 1 = Male 2 = Female Artichoke Preference 1 = Prefer Artichokes 2 = Don’t Prefer Artichokes A 1 2 B 2 1 C 1 2 D 2 1 E 2 1 F 1 2 G 1 2
This is an example of: Dichotomous Data Study Participant Gender 1 = Male 2 = Female Artichoke Preference 1 = Prefer Artichokes 2 = Don’t Prefer Artichokes A 1 2 B 2 1 C 1 2 D 2 1 E 2 1 F 1 2 G 1 2
This is an example of: Dichotomous Data Study Participant Gender 1 = Male 2 = Female by Dichotomous Data Artichoke Preference 1 = Prefer Artichokes 2 = Don’t Prefer Artichokes A 1 2 B 2 1 C 1 2 D 2 1 E 2 1 F 1 2 G 1 2
As you will learn, there is a specific statistical method used to calculate the relationship between two dichotomous variables. It is called the Phi-coefficient.
Note - a dichotomous variable is also a nominal variable.
Note - a dichotomous variable is also a nominal variable. However, nominal variables can also take on more than two values:
Note - a dichotomous variable is also a nominal variable. However, nominal variables can also take on more than two values: 1 = American 2 = Canadian 3 = Mexican like so
Note - a dichotomous variable is also a nominal variable. However, nominal variables can also take on more than two values: 1 = American 2 = Canadian 3 = Mexican Dichotomous nominal variables can only take on two values - (e.g., 1 = Male, 2 = Female)
The next type of relationship involves dichotomous by scaled variables.
The next type of relationship involves dichotomous by scaled variables. Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable
Now you already know what a dichotomous variable is, but what is a scaled variable?
A scaled variable is a variable that theoretically can take on an infinite amount of values.
A scaled variable is a variable that theoretically can take on an infinite amount of values.
For example,
Let's say a car can go as slow as 0 miles per hour and as fast as 130 miles per hour.
Within those two points (0 and 130mph) it could go 30 mph, 60 mph, 23 mph, 120 mph, 33.2 mph, 44.302 mph, or even 88.00000000001 mph.
The point is that between these two points (0 and 130mph) there are an infinite number of values that the speed could take.
Scaled data also has what are called equal intervals.
Scaled data also has what are called equal intervals. This means that the basic unit of measurement (e.g., inches, miles per hour, pounds) are the same across the scale:
Scaled data also has what are called equal intervals. This means that the basic unit of measurement (e.g., inches, miles per hour, pounds) are the same across the scale: 100o - 101o 70o - 71o 40o - 41o Each set of readings are the same distance apart: 1o Slide 51
Here is an example of a word problem with scaled by dichotomous variables:
You have been asked to determine the relationship between age and hours of sleep. Age is divided into two groups: Middle Age (45- 64) and Old Age (65-94).
You have been asked to determine the relationship between age and hours of sleep. Age is divided into two groups: Middle Age (45- 64) and Old Age (65-94). The Scaled Variable is hours of sleep which can take on values from 0 to 8+ hours.
You have been asked to determine the relationship between age and hours of sleep. Age is divided into two groups: Middle Age (45- 64) and Old Age (65-94). The Dichotomous Variable is age which in this case can take on two values (1) middle and (2) old age.
Here is what the data set might look like:
Here is what the data set might look like: Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
Here is what the data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
Here is what the data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
Here is what the data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep by A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
Here is what the data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Scaled Data Hours of Sleep by A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
Note, in the strictest sense scaled data should be like the car example (values are infinite between 0 and 130 mph).
However, in the social sciences many times data that is technically not scaled (e.g., on a scale of 1-10 how would you rate the ballerina's performance), are still treated as scaled data.
However, in the social sciences many times data that is technically not scaled (e.g., on a scale of 1-10 how would you rate the ballerina's performance), are still treated as scaled data. Yes, it is true there are only 10 values that the variable can take on, but many researchers will treat it as scaled data. For the purposes of this class we will treat variables such as these as scaled data as well.
However, in the social sciences many times data that is technically not scaled (e.g., on a scale of 1-10 how would you rate the ballerina's performance), are still treated as scaled data. Yes, it is true there are only 10 values that the variable can take on, but many researchers will treat it as scaled data. For the purposes of this class we will treat variables such as these as scaled data as well.
However, if we were rating on a scale of 1-2, 1-3 or 1-4 we most likely would not treat such variables as scaled.
As you will learn there is a specific statistical method used to calculate the relationship between scaled by dichotomous variables. it is called the Point Biserial Correlation.
Lastly let's consider the relationship involving ordinal data by another variable.
Lastly let's consider the relationship involving ordinal data by another variable. Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable
An ordinal variable is a variable where the numbers represent relative amounts of a an attribute. However, they do not have equal intervals.
For example,
In this pole vaulting example you will notice that 1st and 2nd place are closer to each other:
In this pole vaulting example you will notice that 1st and 2nd place are closer to each other: 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
In this pole vaulting example you will notice that 1st and 2nd place are closer to each other: 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
In this pole vaulting example you will notice that 1st and 2nd place are closer to each other: 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3” 2 inches apart
. . . than 2nd and 3rd place, which are much further apart
. . . than 2nd and 3rd place, which are much further apart 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
. . . than 2nd and 3rd place, which are much further apart 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3” 3 feet 1” apart
Rank ordered or ordinal data such as these do not have equal intervals. 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
Rank ordered or ordinal data such as these do not have equal intervals. 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
Here is what an ordinal by ordinal problem looks like:
In a study, researchers rank order different breeds of dog based on how high they can jump. They then rank order them based on the length of their hind legs. They wish to determine if a relationship exists between jumping height and hind leg length.
In a study, researchers rank order different breeds of dog based on how high they can jump. They then rank order them based on the length of their hind legs. They wish to determine if a relationship exists between jumping height and hind leg length.
In a study, researchers rank order different breeds of dog based on how high they can jump. They then rank order them based on the length of their hind legs. They wish to determine if a relationship exists between jumping height and hind leg length.
Here’s the data set:
Here’s the data set: Breed Participant Jumping Rank Hind-Leg Length Rank A 1st 2nd B 3rd 6th C 6th 4th D 4th 3rd E 7th 7th F 2nd 1st G 5th 5th
Here’s the data set: Ordinal or Ranked Data Breed Participant Jumping Rank Hind-Leg Length Rank A 1st 2nd B 3rd 6th C 6th 4th D 4th 3rd E 7th 7th F 2nd 1st G 5th 5th
Here’s the data set: by Ordinal or Ranked Data Ordinal or Ranked Data Breed Participant Jumping Rank Hind-Leg Length Rank A 1st 2nd B 3rd 6th C 6th 4th D 4th 3rd E 7th 7th F 2nd 1st G 5th 5th
Rank ordered data can also take the form of percentiles.
Percentiles communicate the percentage of observations or values below a certain point.
If my score on the ACT is at the 35th percentile that means the 35% of ACT takers are below me.
If my score on the ACT is at the 35th percentile that means the 35% of ACT takers are below me.
A data set taken from the dog jumping question might look like this:
A data set taken from the dog jumping question might look like this: Breed Participant Jumping Percentile Rank Hind-Leg Percentile Rank A 99% 85% B 78% 33% C 54% 64% D 69% 73% E 34% 28% F 84% 97% G 61% 54%
A data set taken from the dog jumping question might look like this: Ordinal or Percentile Ranked Data Breed Participant Jumping Percentile Rank Hind-Leg Percentile Rank A 99% 85% B 78% 33% C 54% 64% D 69% 73% E 34% 28% F 84% 97% G 61% 54%
A data set taken from the dog jumping question might look like this: Ordinal or Percentile Ranked Data Breed Participant Jumping Percentile Rank Ordinal or Percentile Ranked Data Hind-Leg Percentile Rank by A 99% 85% B 78% 33% C 54% 64% D 69% 73% E 34% 28% F 84% 97% G 61% 54%
The next example is that of a relationship between ordinal variable and a scaled variable.
You have been asked to determine if there is a relationship between the height of marathon runners and their final ranking in a race.
You have been asked to determine if there is a relationship between the height of marathon runners and their final ranking in a race.
Here’s the data set: Marathon Runners Height in inches Order of Finish A 73 6th B 67 4th C 69 5th D 64 2nd E 71 7th F 62 1st G 66 3rd
Here’s the data set: Scaled Data Marathon Runners Height in inches Order of Finish A 73 6th B 67 4th C 69 5th D 64 2nd E 71 7th F 62 1st G 66 3rd
Here’s the data set: Scaled Data by Ordinal/ Ranked Data Marathon Runners Height in inches Order of Finish A 73 6th B 67 4th C 69 5th D 64 2nd E 71 7th F 62 1st G 66 3rd
The final example is that of a relationship between ordinal variable and a nominal variable.
You have been asked to determine if there is a relationship between gender and spelling bee competition rankings.
You have been asked to determine if there is a relationship between gender and spelling bee competition rankings.
Here’s the data set:
Marathon Runners Gender Spelling Bee Rank A 1 6th B 2 4th C 2 5th D 2 2nd E 1 7th F 1 1st G 2 3rd
Dichotomous/ Nominal Data Marathon Runners Gender Spelling Bee Rank A 1 6th B 2 4th C 2 5th D 2 2nd E 1 7th F 1 1st G 2 3rd
by Ordinal/ Ranked Data Dichotomous/ Nominal Data Marathon Runners Gender Spelling Bee Rank A 1 6th B 2 4th C 2 5th D 2 2nd E 1 7th F 1 1st G 2 3rd
In summary,
In summary, When at least one variable in the relationship is ordinal or rank ordered, then you choose the final option:
In summary, When at least one variable in the relationship is ordinal or rank ordered, then you choose the final option: Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable
As you will learn there are specific statistical methods used to calculate the relationship between ordinal by ordinal or ordinal by other variables.
As you will learn there are specific statistical methods used to calculate the relationship between ordinal by ordinal or ordinal by other variables. They are the Spearman Rho and Kendall Tau.
As you will learn there are specific statistical methods used to calculate the relationship between ordinal by ordinal or ordinal by other variables. They are the Spearman Rho and Kendall Tau. We'll explain their difference in another presentation.
A final note:
Dichotomous data like this: 1 = Catholic 2 = Mormon
Dichotomous data like this: 1 = Catholic 2 = Mormon Study Participants Religious Affiliation 1 = Catholic 2 = Mormon A 1 B 1 C 1 D 2 E 1 F 2
Dichotomous data like this: 1 = Catholic 2 = Mormon Study Participants Religious Affiliation 1 = Catholic 2 = Mormon A 1 B 1 C 1 D 2 E 1 F 2
Dichotomous data like this: 1 = Catholic 2 = Mormon . . . can become scaled if we are talking about the number of Catholics or Mormons.
Dichotomous data like this: 1 = Catholic 2 = Mormon Event Number of Catholics in attendance Number of Mormons in attendance A 120 22 B 322 34 C 401 78 D 73 55 E 80 3 F 392 102 . . . can become scaled if we are talking about the number of Catholics or Mormons.
Dichotomous data like this: 1 = Catholic 2 = Mormon Event Number of Catholics in attendance Number of Mormons in attendance A 120 22 B 322 34 C 401 78 D 73 55 E 80 3 F 392 102 . . . can become scaled if we are talking about the number of Catholics or Mormons.
Which option is most appropriate for the problem you are working with: Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable

More Related Content

PPTX
Presentation1
byNavjyoti Sharma
 
PPTX
Modified Input (Foreigner Talk)
bySawsan Ali
 
PPSX
Genetic_Algorithm_AI(TU)
byKapil Khatiwada
 
PPT
Eng 345 powerpoint
bysawhit2
 
PPT
Audio visual method
byRebeca Roman
 
PPTX
Critical Linguist and Critycal Discourse Analysis
byliveistoshare
 
PPTX
AM and FM Transmitters and receivers
byKavitaGiri5
 
PPTX
Booth’s algorithm.(a014& a015)
byPiyush Rochwani
 
Presentation1
byNavjyoti Sharma
 
Modified Input (Foreigner Talk)
bySawsan Ali
 
Genetic_Algorithm_AI(TU)
byKapil Khatiwada
 
Eng 345 powerpoint
bysawhit2
 
Audio visual method
byRebeca Roman
 
Critical Linguist and Critycal Discourse Analysis
byliveistoshare
 
AM and FM Transmitters and receivers
byKavitaGiri5
 
Booth’s algorithm.(a014& a015)
byPiyush Rochwani
 

Similar to The nature of the data

PPTX
The Nature of the Data - Relationships
byKen Plummer
 
PPTX
Quick reminder nature of the data
byKen Plummer
 
PDF
Tetrachoric Correlation - Thiyagu
byThiyagu K
 
PPTX
Types of variables in research
byDr. Ankita Chaturvedi
 
PPT
Measurement_and_Measurement_Scales
byrukhsana khan
 
PPT
Stats-Review-Maie-St-John-5-20-2009.ppt
byDiptoKumerSarker1
 
PDF
Data Analysis with SPSS PPT.pdf
byThanavathi C
 
PPTX
Research - Quarter2 - W2 - Variables.pptx
byElyssaChriselleBarce1
 
PPTX
Types of variables in research for grade 7 research
byJCtutor
 
DOCX
typesofvariablesinresearchankitach-181022084515.docx
bysaranya443113
 
PDF
Unit 4 rm
byRameshkumarM15
 
PPTX
Lecture 06 (Scales of Measurement).pptx
byKamiBhutta
 
PPTX
Biomedical statistics
byAbdullaAhmad6
 
PPTX
variables of research for research subjects
byDINAHOANI1
 
PDF
ANSWER TO MODULE 5 ASSIGNMENT Essay
byTammy Moncrief
 
PPT
Descriptive stats
bysungwon_ciel
 
PPTX
Non parametric relationship - practice problems
byKen Plummer
 
DOCX
Types of Statistical Analyses MatrixCarrington Sherman, Donn.docx
bymarilucorr
 
PPTX
1. INTRODUCTION TO STATISTICS, TYPES OF DATA, VARIABLE.pptx
byManikaA2
 
PPTX
Other correlation coefficients
byJuan Apolinario Reyes
 
The Nature of the Data - Relationships
byKen Plummer
 
Quick reminder nature of the data
byKen Plummer
 
Tetrachoric Correlation - Thiyagu
byThiyagu K
 
Types of variables in research
byDr. Ankita Chaturvedi
 
Measurement_and_Measurement_Scales
byrukhsana khan
 
Stats-Review-Maie-St-John-5-20-2009.ppt
byDiptoKumerSarker1
 
Data Analysis with SPSS PPT.pdf
byThanavathi C
 
Research - Quarter2 - W2 - Variables.pptx
byElyssaChriselleBarce1
 
Types of variables in research for grade 7 research
byJCtutor
 
typesofvariablesinresearchankitach-181022084515.docx
bysaranya443113
 
Unit 4 rm
byRameshkumarM15
 
Lecture 06 (Scales of Measurement).pptx
byKamiBhutta
 
Biomedical statistics
byAbdullaAhmad6
 
variables of research for research subjects
byDINAHOANI1
 
ANSWER TO MODULE 5 ASSIGNMENT Essay
byTammy Moncrief
 
Descriptive stats
bysungwon_ciel
 
Non parametric relationship - practice problems
byKen Plummer
 
Types of Statistical Analyses MatrixCarrington Sherman, Donn.docx
bymarilucorr
 
1. INTRODUCTION TO STATISTICS, TYPES OF DATA, VARIABLE.pptx
byManikaA2
 
Other correlation coefficients
byJuan Apolinario Reyes
 

More from Ken Plummer

PPTX
Diff rel gof-fit - jejit - practice (5)
byKen Plummer
 
PPTX
Learn About Range - Copyright updated
byKen Plummer
 
PPTX
Inferential vs descriptive tutorial of when to use - Copyright Updated
byKen Plummer
 
PPTX
Diff rel ind-fit practice - Copyright Updated
byKen Plummer
 
PPTX
Normal or skewed distributions (inferential) - Copyright updated
byKen Plummer
 
PPTX
Normal or skewed distributions (descriptive both2) - Copyright updated
byKen Plummer
 
PPTX
Nature of the data practice - Copyright updated
byKen Plummer
 
PPTX
Nature of the data (spread) - Copyright updated
byKen Plummer
 
PPTX
Mode practice 1 - Copyright updated
byKen Plummer
 
PPTX
Nature of the data (descriptive) - Copyright updated
byKen Plummer
 
PPTX
Dichotomous or scaled
byKen Plummer
 
PPTX
Skewed less than 30 (ties)
byKen Plummer
 
PPTX
Skewed sample size less than 30
byKen Plummer
 
PPTX
Ordinal (ties)
byKen Plummer
 
PPTX
Ordinal and nominal
byKen Plummer
 
PPTX
Relationship covariates
byKen Plummer
 
PPTX
Relationship nature of data
byKen Plummer
 
PPTX
Number of variables (predictive)
byKen Plummer
 
PPTX
Levels of the iv
byKen Plummer
 
PPTX
Independent variables (2)
byKen Plummer
 
Diff rel gof-fit - jejit - practice (5)
byKen Plummer
 
Learn About Range - Copyright updated
byKen Plummer
 
Inferential vs descriptive tutorial of when to use - Copyright Updated
byKen Plummer
 
Diff rel ind-fit practice - Copyright Updated
byKen Plummer
 
Normal or skewed distributions (inferential) - Copyright updated
byKen Plummer
 
Normal or skewed distributions (descriptive both2) - Copyright updated
byKen Plummer
 
Nature of the data practice - Copyright updated
byKen Plummer
 
Nature of the data (spread) - Copyright updated
byKen Plummer
 
Mode practice 1 - Copyright updated
byKen Plummer
 
Nature of the data (descriptive) - Copyright updated
byKen Plummer
 
Dichotomous or scaled
byKen Plummer
 
Skewed less than 30 (ties)
byKen Plummer
 
Skewed sample size less than 30
byKen Plummer
 
Ordinal (ties)
byKen Plummer
 
Ordinal and nominal
byKen Plummer
 
Relationship covariates
byKen Plummer
 
Relationship nature of data
byKen Plummer
 
Number of variables (predictive)
byKen Plummer
 
Levels of the iv
byKen Plummer
 
Independent variables (2)
byKen Plummer
 

Recently uploaded

PDF
Toward Massive, Ultrareliable, and Low-Latency Wireless Communication With Sh...
byMan_Ebook
 
PPTX
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
PPTX
Filipino 11-Tekstong Prosidyural-Final.pptx
byMargieBAlmoza
 
PPTX
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
PPTX
AI_in_Daily_Life_Presentation and more.pptx
bybantydansena
 
PPTX
Searching in PubMed andCochrane_Practical Presentation.pptx
bySystematic Reviews Network (SRN)
 
PDF
APM Wessex Network: DEIB Policy into Practice
byAssociation for Project Management
 
PPTX
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
PPTX
ICH Harmonization A Global Pathway to Unified Drug Regulation.pptx
byDr. Smita Kumbhar
 
PPTX
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PDF
TOM STOPPARD (1937 - 2025) - THE MIND AS A STAGE, THE STAGE AS DESTINY .pdf
byMilanStankovic19
 
PPTX
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
PDF
NAVIGATE PHARMACY CAREER OPPORTUNITIES.pdf
byMd. Zakaria Faruki
 
PDF
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
PDF
Unit-III pdf (Basic listening Skill, Effective Writing Communication & Writin...
bySayyadTarannum
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PPTX
How to Manage Line Discounts in Odoo 18 POS
byCeline George
 
PDF
Biology Practical Class 12th 2025 PDF(2)-2-52.pdf
bySCPRPWomenCollegeChi
 
PDF
Blood Group Incompatibility: Rh Factor and Erythroblastosis Fetalis
bySudhandraKarthi
 
Toward Massive, Ultrareliable, and Low-Latency Wireless Communication With Sh...
byMan_Ebook
 
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
Filipino 11-Tekstong Prosidyural-Final.pptx
byMargieBAlmoza
 
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
AI_in_Daily_Life_Presentation and more.pptx
bybantydansena
 
Searching in PubMed andCochrane_Practical Presentation.pptx
bySystematic Reviews Network (SRN)
 
APM Wessex Network: DEIB Policy into Practice
byAssociation for Project Management
 
Vitamins and mineral deficiency , signs and symptoms associated with exercise
byvirupa chandrika reddy
 
ICH Harmonization A Global Pathway to Unified Drug Regulation.pptx
byDr. Smita Kumbhar
 
Pig- piggy bank in Big Data Analytics.ppt.pptx
byVarshini M
 
Analyzing the data of your initial survey
byThelma Villaflores
 
TOM STOPPARD (1937 - 2025) - THE MIND AS A STAGE, THE STAGE AS DESTINY .pdf
byMilanStankovic19
 
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
NAVIGATE PHARMACY CAREER OPPORTUNITIES.pdf
byMd. Zakaria Faruki
 
DHA/HAAD/MOH/DOH OPTOMETRY MCQ PYQ. .pdf
byAnmol Singh
 
Unit-III pdf (Basic listening Skill, Effective Writing Communication & Writin...
bySayyadTarannum
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
How to Manage Line Discounts in Odoo 18 POS
byCeline George
 
Biology Practical Class 12th 2025 PDF(2)-2-52.pdf
bySCPRPWomenCollegeChi
 
Blood Group Incompatibility: Rh Factor and Erythroblastosis Fetalis
bySudhandraKarthi
 

The nature of the data

  • 1.
    The Nature ofYour Data
  • 2.
    The purpose ofthis presentation is to help you determine if the two data sets you are working with in this problem are:
  • 3.
    The purpose ofthis presentation is to help you determine if the two data sets you are working with in this problem are: Dichotomous by Dichotomous Dichotomous by Scaled or Ordinal by Another Variable
  • 4.
    First, let's define what each of these mean. Dichotomous by Dichotomous Dichotomous by Scaled or Ordinal by Ordinal
  • 5.
  • 6.
  • 7.
    The "Di" inDichotomous means "two"
  • 8.
    . . .and "tomous" or "tomy" as in “appendec-tomy” means to divide by.
  • 9.
    . . .and "tomous" or "tomy" as in “appendec-tomy” means to divide by.
  • 10.
    So, dichotomous meansto divide by two.
  • 11.
    In this casea variable is divided by two or specifically it can only take on two values.
  • 12.
  • 13.
    Gender is agood example of a dichotomous data.
  • 14.
    Gender is agood example of a dichotomous data. It generally takes on two values
  • 15.
    Gender is agood example of a dichotomous data. It generally takes on two values (1) male (2) female
  • 16.
    In some casesindividuals are divided by (1) those who received a treatment and (2) those who did not.
  • 17.
  • 18.
    You have beenasked to determine if those who eat asparagus score higher on a well-being scale (1-10) than those who do not.
  • 19.
    You have beenasked to determine if those who eat asparagus score higher on a well-being scale (1-10) than those who do not.
  • 20.
    You have beenasked to determine if those who eat asparagus score higher on a well-being scale (1-10) than those who do not. In this case, we are dealing with those (1) who eat asparagus and those (2) who do not.
  • 21.
    With dichotomous bydichotomous data you are examining the relationship between two dichotomous variables.
  • 22.
    Here is anexample:
  • 23.
    It has beenpurported that females prefer artichokes more than do males.
  • 24.
    It has beenpurported that females prefer artichokes more than do males.
  • 25.
    It has beenpurported that females prefer artichokes more than do males. Dichotomous variable 1: Gender (1)Male (2)Female
  • 26.
    It has beenpurported that females prefer artichokes more than do males. Dichotomous variable 1: Gender (1)Male (2)Female
  • 27.
    It has beenpurported that females prefer artichokes more than do males. Dichotomous variable 1: Gender (1)Male (2)Female
  • 28.
    It has beenpurported that females prefer artichokes more than do males. Dichotomous variable 2: Artichoke Preference (1)Prefer Artichokes (2)Do not prefer Artichokes
  • 29.
    It has beenpurported that females prefer artichokes more than do males. Dichotomous variable 2: Artichoke Preference (1)Prefer Artichokes (2)Do not prefer Artichokes
  • 30.
    It has beenpurported that females prefer artichokes more than do males. Dichotomous variable 2: Artichoke Preference (1)Prefer Artichokes (2)Do not prefer Artichokes
  • 31.
    Here is whatthe data set looks like:
  • 32.
    It has beenpurported that females prefer artichokes more than do males. Study Participant Gender 1 = Male 2 = Female Artichoke Preference 1 = Prefer Artichokes 2 = Don’t Prefer Artichokes A 1 2 B 2 1 C 1 2 D 2 1 E 2 1 F 1 2 G 1 2
  • 33.
    This is anexample of: Dichotomous Data Study Participant Gender 1 = Male 2 = Female Artichoke Preference 1 = Prefer Artichokes 2 = Don’t Prefer Artichokes A 1 2 B 2 1 C 1 2 D 2 1 E 2 1 F 1 2 G 1 2
  • 34.
    This is anexample of: Dichotomous Data Study Participant Gender 1 = Male 2 = Female by Dichotomous Data Artichoke Preference 1 = Prefer Artichokes 2 = Don’t Prefer Artichokes A 1 2 B 2 1 C 1 2 D 2 1 E 2 1 F 1 2 G 1 2
  • 35.
    As you willlearn, there is a specific statistical method used to calculate the relationship between two dichotomous variables. It is called the Phi-coefficient.
  • 36.
    Note - adichotomous variable is also a nominal variable.
  • 37.
    Note - adichotomous variable is also a nominal variable. However, nominal variables can also take on more than two values:
  • 38.
    Note - adichotomous variable is also a nominal variable. However, nominal variables can also take on more than two values: 1 = American 2 = Canadian 3 = Mexican like so
  • 39.
    Note - adichotomous variable is also a nominal variable. However, nominal variables can also take on more than two values: 1 = American 2 = Canadian 3 = Mexican Dichotomous nominal variables can only take on two values - (e.g., 1 = Male, 2 = Female)
  • 40.
    The next typeof relationship involves dichotomous by scaled variables.
  • 41.
    The next typeof relationship involves dichotomous by scaled variables. Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable
  • 42.
    Now you alreadyknow what a dichotomous variable is, but what is a scaled variable?
  • 43.
    A scaled variableis a variable that theoretically can take on an infinite amount of values.
  • 44.
    A scaled variableis a variable that theoretically can take on an infinite amount of values.
  • 45.
  • 46.
    Let's say acar can go as slow as 0 miles per hour and as fast as 130 miles per hour.
  • 47.
    Within those twopoints (0 and 130mph) it could go 30 mph, 60 mph, 23 mph, 120 mph, 33.2 mph, 44.302 mph, or even 88.00000000001 mph.
  • 48.
    The point isthat between these two points (0 and 130mph) there are an infinite number of values that the speed could take.
  • 49.
    Scaled data alsohas what are called equal intervals.
  • 50.
    Scaled data alsohas what are called equal intervals. This means that the basic unit of measurement (e.g., inches, miles per hour, pounds) are the same across the scale:
  • 51.
    Scaled data alsohas what are called equal intervals. This means that the basic unit of measurement (e.g., inches, miles per hour, pounds) are the same across the scale: 100o - 101o 70o - 71o 40o - 41o Each set of readings are the same distance apart: 1o Slide 51
  • 52.
    Here is anexample of a word problem with scaled by dichotomous variables:
  • 53.
    You have beenasked to determine the relationship between age and hours of sleep. Age is divided into two groups: Middle Age (45- 64) and Old Age (65-94).
  • 54.
    You have beenasked to determine the relationship between age and hours of sleep. Age is divided into two groups: Middle Age (45- 64) and Old Age (65-94). The Scaled Variable is hours of sleep which can take on values from 0 to 8+ hours.
  • 55.
    You have beenasked to determine the relationship between age and hours of sleep. Age is divided into two groups: Middle Age (45- 64) and Old Age (65-94). The Dichotomous Variable is age which in this case can take on two values (1) middle and (2) old age.
  • 56.
    Here is whatthe data set might look like:
  • 57.
    Here is whatthe data set might look like: Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
  • 58.
    Here is whatthe data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
  • 59.
    Here is whatthe data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
  • 60.
    Here is whatthe data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Hours of Sleep by A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
  • 61.
    Here is whatthe data set might look like: Dichotomous Data Study Participant Age 1 = 45-64 years 2 = 65-94 years Scaled Data Hours of Sleep by A 1 6.2 B 2 9.1 C 1 5.8 D 2 8.2 E 2 7.4 F 1 4.9 G 1 6.8
  • 62.
    Note, in thestrictest sense scaled data should be like the car example (values are infinite between 0 and 130 mph).
  • 63.
    However, in thesocial sciences many times data that is technically not scaled (e.g., on a scale of 1-10 how would you rate the ballerina's performance), are still treated as scaled data.
  • 64.
    However, in thesocial sciences many times data that is technically not scaled (e.g., on a scale of 1-10 how would you rate the ballerina's performance), are still treated as scaled data. Yes, it is true there are only 10 values that the variable can take on, but many researchers will treat it as scaled data. For the purposes of this class we will treat variables such as these as scaled data as well.
  • 65.
    However, in thesocial sciences many times data that is technically not scaled (e.g., on a scale of 1-10 how would you rate the ballerina's performance), are still treated as scaled data. Yes, it is true there are only 10 values that the variable can take on, but many researchers will treat it as scaled data. For the purposes of this class we will treat variables such as these as scaled data as well.
  • 66.
    However, if wewere rating on a scale of 1-2, 1-3 or 1-4 we most likely would not treat such variables as scaled.
  • 67.
    As you willlearn there is a specific statistical method used to calculate the relationship between scaled by dichotomous variables. it is called the Point Biserial Correlation.
  • 68.
    Lastly let's considerthe relationship involving ordinal data by another variable.
  • 69.
    Lastly let's considerthe relationship involving ordinal data by another variable. Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable
  • 70.
    An ordinal variableis a variable where the numbers represent relative amounts of a an attribute. However, they do not have equal intervals.
  • 71.
  • 72.
    In this polevaulting example you will notice that 1st and 2nd place are closer to each other:
  • 73.
    In this polevaulting example you will notice that 1st and 2nd place are closer to each other: 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
  • 74.
    In this polevaulting example you will notice that 1st and 2nd place are closer to each other: 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
  • 75.
    In this polevaulting example you will notice that 1st and 2nd place are closer to each other: 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3” 2 inches apart
  • 76.
    . . .than 2nd and 3rd place, which are much further apart
  • 77.
    . . .than 2nd and 3rd place, which are much further apart 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
  • 78.
    . . .than 2nd and 3rd place, which are much further apart 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3” 3 feet 1” apart
  • 79.
    Rank ordered orordinal data such as these do not have equal intervals. 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
  • 80.
    Rank ordered orordinal data such as these do not have equal intervals. 3rd Place 15’ 2” 2nd Place 18’ 1” 1st Place 18’ 3”
  • 81.
    Here is whatan ordinal by ordinal problem looks like:
  • 82.
    In a study,researchers rank order different breeds of dog based on how high they can jump. They then rank order them based on the length of their hind legs. They wish to determine if a relationship exists between jumping height and hind leg length.
  • 83.
    In a study,researchers rank order different breeds of dog based on how high they can jump. They then rank order them based on the length of their hind legs. They wish to determine if a relationship exists between jumping height and hind leg length.
  • 84.
    In a study,researchers rank order different breeds of dog based on how high they can jump. They then rank order them based on the length of their hind legs. They wish to determine if a relationship exists between jumping height and hind leg length.
  • 85.
  • 86.
    Here’s the dataset: Breed Participant Jumping Rank Hind-Leg Length Rank A 1st 2nd B 3rd 6th C 6th 4th D 4th 3rd E 7th 7th F 2nd 1st G 5th 5th
  • 87.
    Here’s the dataset: Ordinal or Ranked Data Breed Participant Jumping Rank Hind-Leg Length Rank A 1st 2nd B 3rd 6th C 6th 4th D 4th 3rd E 7th 7th F 2nd 1st G 5th 5th
  • 88.
    Here’s the dataset: by Ordinal or Ranked Data Ordinal or Ranked Data Breed Participant Jumping Rank Hind-Leg Length Rank A 1st 2nd B 3rd 6th C 6th 4th D 4th 3rd E 7th 7th F 2nd 1st G 5th 5th
  • 89.
    Rank ordered datacan also take the form of percentiles.
  • 90.
    Percentiles communicate thepercentage of observations or values below a certain point.
  • 91.
    If my scoreon the ACT is at the 35th percentile that means the 35% of ACT takers are below me.
  • 92.
    If my scoreon the ACT is at the 35th percentile that means the 35% of ACT takers are below me.
  • 93.
    A data settaken from the dog jumping question might look like this:
  • 94.
    A data settaken from the dog jumping question might look like this: Breed Participant Jumping Percentile Rank Hind-Leg Percentile Rank A 99% 85% B 78% 33% C 54% 64% D 69% 73% E 34% 28% F 84% 97% G 61% 54%
  • 95.
    A data settaken from the dog jumping question might look like this: Ordinal or Percentile Ranked Data Breed Participant Jumping Percentile Rank Hind-Leg Percentile Rank A 99% 85% B 78% 33% C 54% 64% D 69% 73% E 34% 28% F 84% 97% G 61% 54%
  • 96.
    A data settaken from the dog jumping question might look like this: Ordinal or Percentile Ranked Data Breed Participant Jumping Percentile Rank Ordinal or Percentile Ranked Data Hind-Leg Percentile Rank by A 99% 85% B 78% 33% C 54% 64% D 69% 73% E 34% 28% F 84% 97% G 61% 54%
  • 97.
    The next exampleis that of a relationship between ordinal variable and a scaled variable.
  • 98.
    You have beenasked to determine if there is a relationship between the height of marathon runners and their final ranking in a race.
  • 99.
    You have beenasked to determine if there is a relationship between the height of marathon runners and their final ranking in a race.
  • 100.
    Here’s the dataset: Marathon Runners Height in inches Order of Finish A 73 6th B 67 4th C 69 5th D 64 2nd E 71 7th F 62 1st G 66 3rd
  • 101.
    Here’s the dataset: Scaled Data Marathon Runners Height in inches Order of Finish A 73 6th B 67 4th C 69 5th D 64 2nd E 71 7th F 62 1st G 66 3rd
  • 102.
    Here’s the dataset: Scaled Data by Ordinal/ Ranked Data Marathon Runners Height in inches Order of Finish A 73 6th B 67 4th C 69 5th D 64 2nd E 71 7th F 62 1st G 66 3rd
  • 103.
    The final exampleis that of a relationship between ordinal variable and a nominal variable.
  • 104.
    You have beenasked to determine if there is a relationship between gender and spelling bee competition rankings.
  • 105.
    You have beenasked to determine if there is a relationship between gender and spelling bee competition rankings.
  • 106.
  • 107.
    Marathon Runners GenderSpelling Bee Rank A 1 6th B 2 4th C 2 5th D 2 2nd E 1 7th F 1 1st G 2 3rd
  • 108.
    Dichotomous/ Nominal Data Marathon Runners Gender Spelling Bee Rank A 1 6th B 2 4th C 2 5th D 2 2nd E 1 7th F 1 1st G 2 3rd
  • 109.
    by Ordinal/ RankedData Dichotomous/ Nominal Data Marathon Runners Gender Spelling Bee Rank A 1 6th B 2 4th C 2 5th D 2 2nd E 1 7th F 1 1st G 2 3rd
  • 110.
  • 111.
    In summary, Whenat least one variable in the relationship is ordinal or rank ordered, then you choose the final option:
  • 112.
    In summary, Whenat least one variable in the relationship is ordinal or rank ordered, then you choose the final option: Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable
  • 113.
    As you willlearn there are specific statistical methods used to calculate the relationship between ordinal by ordinal or ordinal by other variables.
  • 114.
    As you willlearn there are specific statistical methods used to calculate the relationship between ordinal by ordinal or ordinal by other variables. They are the Spearman Rho and Kendall Tau.
  • 115.
    As you willlearn there are specific statistical methods used to calculate the relationship between ordinal by ordinal or ordinal by other variables. They are the Spearman Rho and Kendall Tau. We'll explain their difference in another presentation.
  • 116.
  • 117.
    Dichotomous data likethis: 1 = Catholic 2 = Mormon
  • 118.
    Dichotomous data likethis: 1 = Catholic 2 = Mormon Study Participants Religious Affiliation 1 = Catholic 2 = Mormon A 1 B 1 C 1 D 2 E 1 F 2
  • 119.
    Dichotomous data likethis: 1 = Catholic 2 = Mormon Study Participants Religious Affiliation 1 = Catholic 2 = Mormon A 1 B 1 C 1 D 2 E 1 F 2
  • 120.
    Dichotomous data likethis: 1 = Catholic 2 = Mormon . . . can become scaled if we are talking about the number of Catholics or Mormons.
  • 121.
    Dichotomous data likethis: 1 = Catholic 2 = Mormon Event Number of Catholics in attendance Number of Mormons in attendance A 120 22 B 322 34 C 401 78 D 73 55 E 80 3 F 392 102 . . . can become scaled if we are talking about the number of Catholics or Mormons.
  • 122.
    Dichotomous data likethis: 1 = Catholic 2 = Mormon Event Number of Catholics in attendance Number of Mormons in attendance A 120 22 B 322 34 C 401 78 D 73 55 E 80 3 F 392 102 . . . can become scaled if we are talking about the number of Catholics or Mormons.
  • 123.
    Which option ismost appropriate for the problem you are working with: Dichotomous by Dichotomous Dichotomous by Scaled Ordinal by Another Variable

Editor's Notes