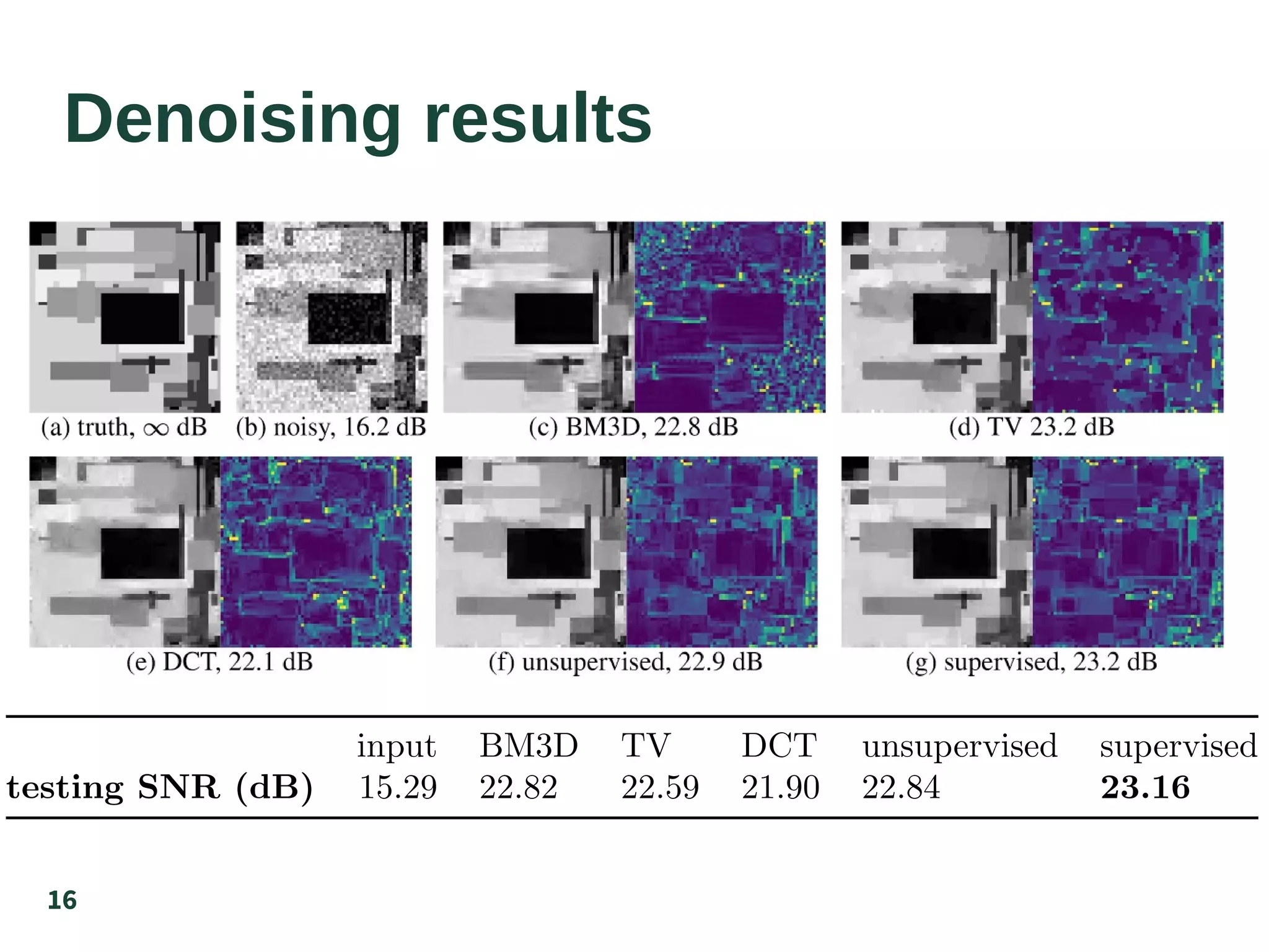
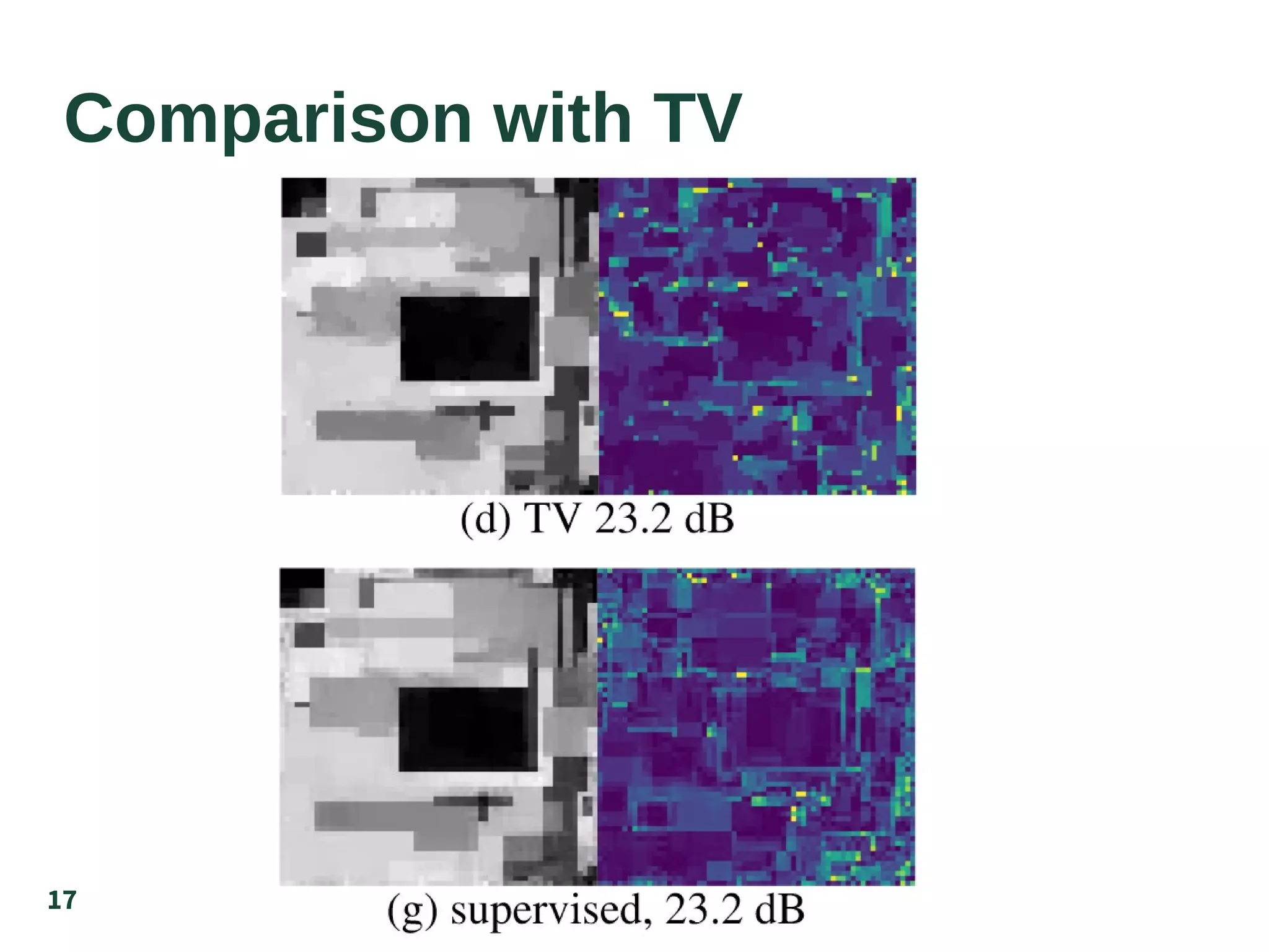
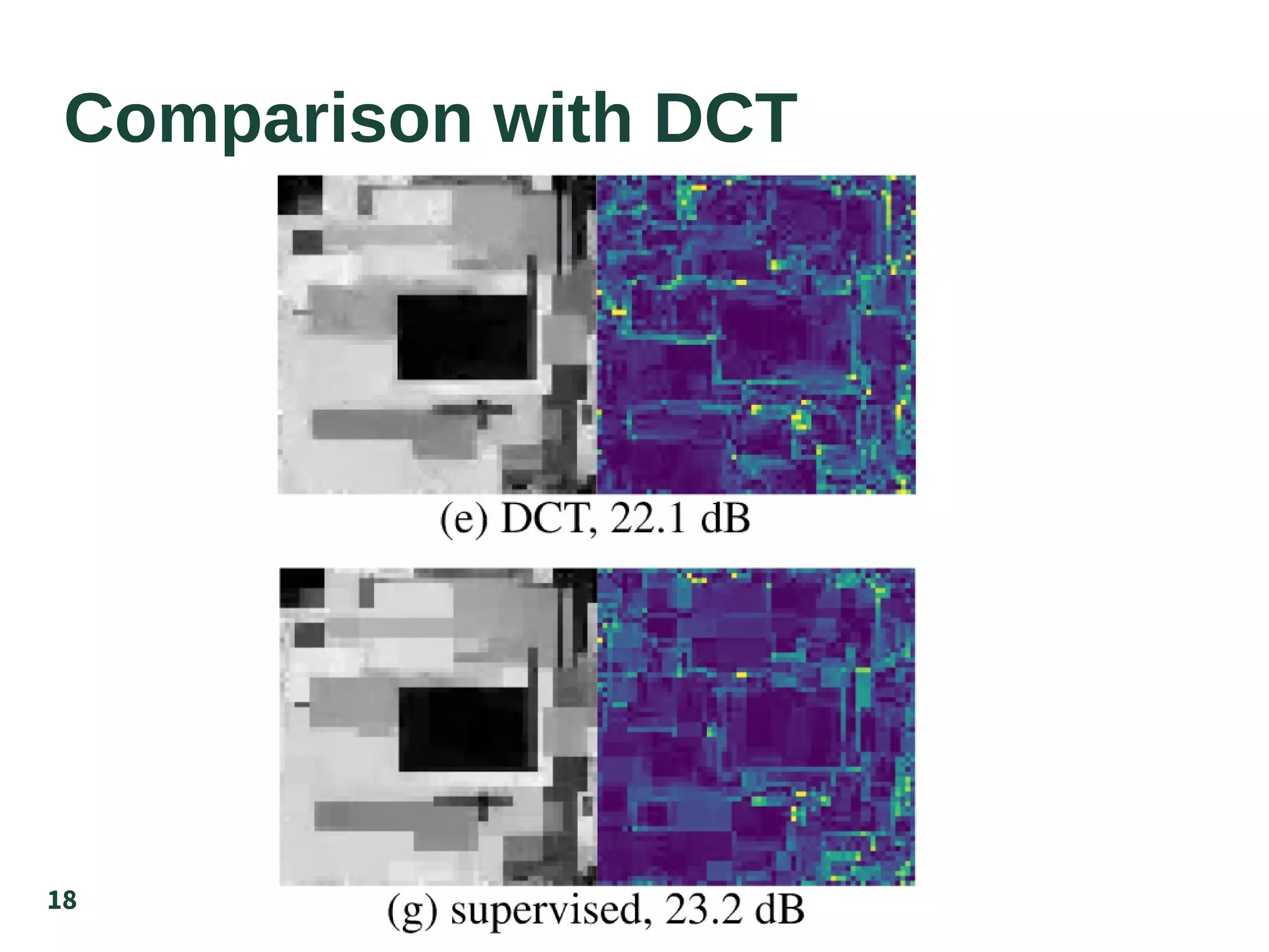
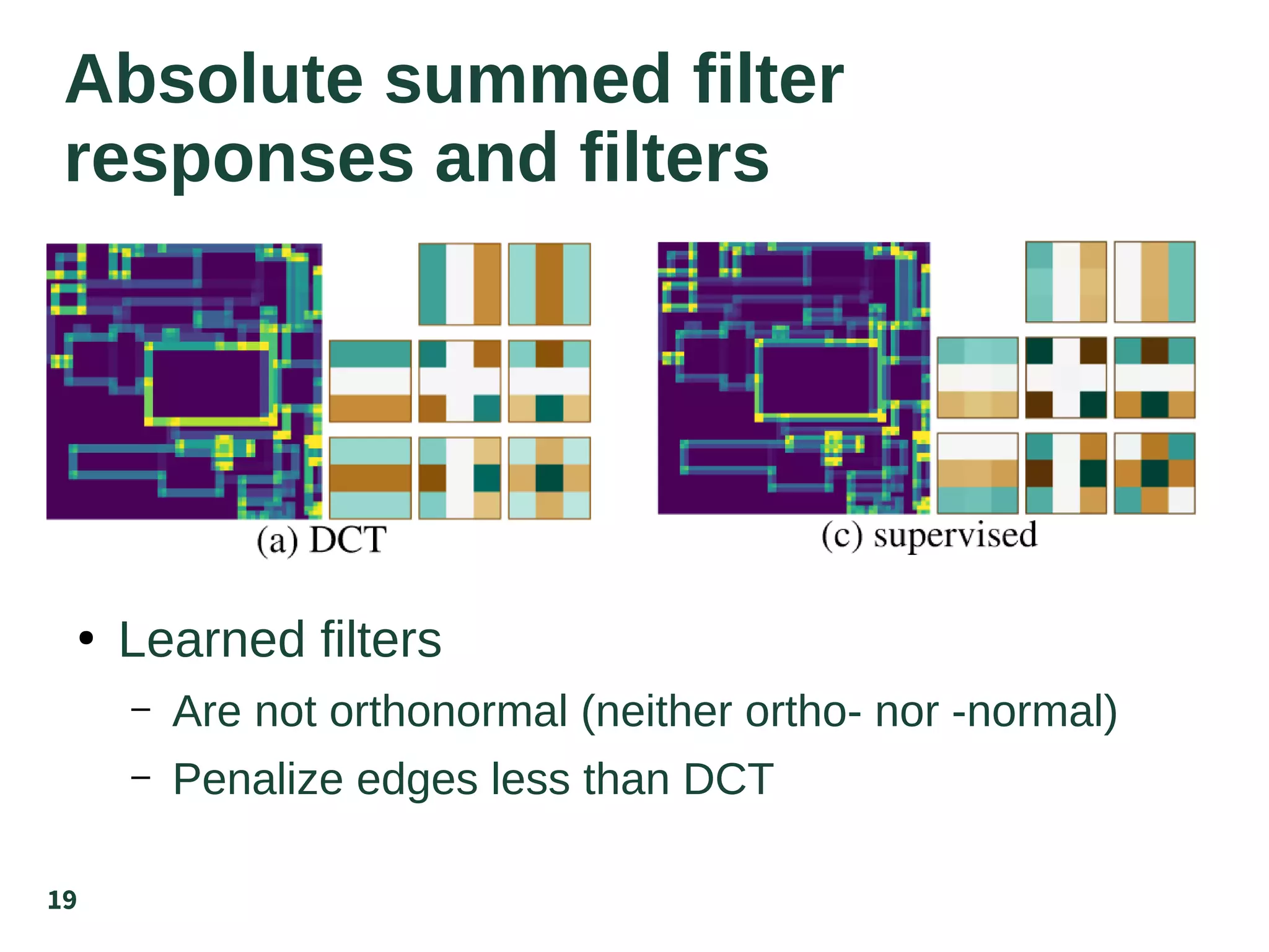
The document discusses the supervised learning of sparsity-promoting regularizers for denoising, comparing various methods such as learned operators with traditional techniques like TV and DCT. It presents a new approach involving gradient descent and provides results from denoising experiments using 64x64 images affected by Gaussian noise. The authors suggest future research directions, including comparisons with CNN-based denoising and extensions to nonuniqueness in reconstruction problems.

1. Supervised Learning of Sparsity-
Promoting Regularizers for Denoising
Michael McCann and Saiprasad Ravishankar
Michigan State University
July 7, 2020 - SIAM Conference on Imaging Science (IS20)

2. 2
What beats a CNN on few-view
X-ray CT reconstruction?
(figure: Jin et al. 2017)
???
“TV is optimal on piecewise constant images”

3. 3
What beats a CNN on few-view
X-ray CT reconstruction?
(figures and table: Adler et al. 2017)
“Hmmm...”

4. 4
Sparsity-promoting regularization
(Candes et al. 2004)
●
Goal: solve the undetermined problem

5. 5
Choosing the sparsifying
operator W
●
Fixed: DCT, TV, wavelets, …
●
Learned: dictionary, transform learning, …
●
Can we do better?
●
What is the optimal operator for a set of images?

6. 6
Related work
●
Peyré et al. 2011; Mairal et al. 2012;
Sprechmann et al. 2013; Chen et al. 2014
●
Main approach: relax the l1 term

7. 7
Our approach
●
Find a closed-form expression for x*
●
Derive gradient of Q wrt parameters
●
Perform stochastic gradient descent

8. 8
Nonsmooth? Nonconvex?
●
1d example: APPROVED

9. 9
Closed form expression for x*(W)
●
Key element: sign pattern of Wx
●
Matrices to select zero and nonzero rows of W
●
For all W with a certain c

10. 10
KKT conditions

11. 11
Closed form expression for x*(W)

12. 12
Gradient of Q
●
Just use autograd?
– No! A-1 prevents it
(Minka 2000)

13. 13
Gradient calculation algorithm
●
Solve the reconstruction problem with current
W (we use ADMM)
●
Find the sign pattern of x* and form A and b
– How to handle inexactness of Wx*?
●
Solve the KKT system to find z
●
Solve a least squares problem to find
●
Use autograd to get

14. 14
Denoising experiment
●
Images are 64x64, range is [0,1]
●
Additive IID Gaussian noise, stdev=0.1
●
10 training, 10 testing

15. 15
Methods compared
●
BM3D, TV, DCT
– Regularization strength tuned on training
●
Unsupervised learned operator
– Minimize s.t. orthogonality on training
– Initialized with DCT
●
Supervised learned operator
– SGD with increasing batch size
– Initialized with DCT

16. 16
Denoising results

17. 17
Comparison with TV

18. 18
Comparison with DCT

19. 19
Absolute summed filter
responses and filters
●
Learned filters
– Are not orthonormal (neither ortho- nor -normal)
– Penalize edges less than DCT

20. 20
Future work
●
Make a full comparison with CNN-based
denoising
– Maybe we don’t need deep architectures!
●
Extend to general linear inverse problems
●
Extend to nonunique x*
●
Extend to multilayer regularizers

21. 21
Thanks for your attention!
●
Preprint: https://arxiv.org/abs/2006.05521
●
Slides: https://bit.ly/38uOCoO
– (those are not zeros)
●
Questions: mccann13@msu.edu

22. 22
References
●
K. H. Jin, M. T. McCann, E. Froustey, and M. Unser, “Deep Convolutional Neural Network
for Inverse Problems in Imaging,” IEEE Transactions on Image Processing, vol. 26, no. 9,
pp. 4509–4522, Sep. 2017.
●
J. Adler and O. Öktem, “Solving ill-posed inverse problems using iterative deep neural
networks,” Inverse Problems, vol. 33, no. 12, p. 124007, Nov. 2017.
●
E. J. Candes, J. Romberg, and T. Tao, “Robust uncertainty principles: exact signal
reconstruction from highly incomplete frequency information,” IEEE Transactions on
Information Theory, vol. 52, no. 2, pp. 489–509, Feb. 2006.
●
G. Peyré and J. M. Fadili, “Learning analysis sparsity priors,” in Sampling Theory
and Applications, Singapore, Singapore, May 2011, p. 4.
●
J. Mairal, F. Bach, and J. Ponce, “Task-driven dictionary learning,”IEEE Transactions on
Pattern Analysis and Machine Intelligence, vol. 34, no. 4, pp. 791–804, Apr. 2012.
●
P. Sprechmann, R. Litman, T. Ben Yakar, A. M. Bronstein, and G. Sapiro, “Supervised
sparse analysis and synthesis operators,” inAdvances in Neural Information Processing
Systems 26, 2013, pp. 908–916.
●
Y. Chen, T. Pock, and H. Bischof, “Learning`1-based analysis and synthesis sparsity priors
using bi-level optimization,”arXiv:1401.4105 [cs.CV], Jan. 2014.
●
Y. Chen, R. Ranftl, and T. Pock, “Insights into analysis operator learning: From patch-
based sparse models to higher order MRFs,”IEEE Transactions on Image Processing, vol.
23, no. 3, pp. 1060–1072, Mar. 2014.
●
T. P. Minka, “Old and new matrix algebra useful for statistics,” MIT Media Lab, 2000.