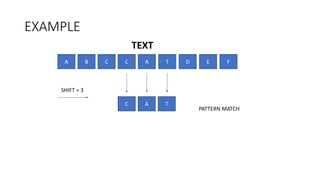
String matching algorithms try to find where a pattern string is found within a larger text string. The naive string matching algorithm compares characters one by one between the pattern and each substring of the text of the same length. The Rabin-Karp algorithm uses a rolling hash to quickly compare the hash of the pattern to the hash of each substring, only doing a full character comparison if the hashes match. Both algorithms output the starting positions in the text where the pattern is found.

2. WHAT IS STRING MATCHING ?
• In computer science, String searching algorithms, sometimes called
string matching algorithms, that try to be find place where one or
several string (also called pattern) are found within a larger string or
text.

3. EXAMPLE
A B C C A T D E F
SHIFT = 3
C A T
PATTERN MATCH
TEXT

4. STRING MATCHING ALGORITHM
• There are many types of String Matching Algorithm like:-
1. The Naive string-matching algorithm.
2. The Rabin-Karp algorithm.
3. String matching with finite automata
4. The Knuth-Morris-Pratt algorithm

5. Naïve String Matching Algorithm
Input: The algorithm takes two strings as input - the text (longer string) and the pattern (shorter string).
Initialization: Let n be the length of the text and m be the length of the pattern.
Loop through the text: For each starting position i from 0 to n - m:
•Initialize a variable j to 0 to track the index in the pattern.
•While j is less than the length of the pattern m and the character at position i + j in the text matches the character at position j in
the pattern:
•Increment j.
•If j equals m, it means the entire pattern has been matched starting at position i.
•Output the position i as the starting index of the pattern in the text.
Repeat: Continue this process for all possible starting positions in the text.
Output: The algorithm outputs the starting positions in the text where the pattern is found.

6. PSEUDO-CODE
• NaiveStringMatch(Text, Pattern):
• n = length(Text)
• m = length(Pattern)
• for i = 0 to n - m
• j = 0
• while j < m and Pattern[j] = Text[i + j]
• j = j + 1
• if j = m
• print "Pattern found at position", i

7. Rabin-Karp Algorithm
Input: The algorithm takes two strings as input - the text (longer string) and the pattern (shorter string).
Initialization:
• Let n be the length of the text and m be the length of the pattern.
• Choose two constants: d, the number of characters in the alphabet, and q, a prime number.
Preprocessing:
• Compute the hash value of the pattern P and the hash value of the first substring of the text t0.
• Iterate over the pattern and the first substring of the text:
• Compute the hash value of the pattern using a rolling hash function: P = (d * P + ASCII value of character) mod q.
• Compute the hash value of the first substring of the text similarly: t0 = (d * t0 + ASCII value of character) mod q.
Matching:
• Slide a window of length m over the text from left to right.
• For each position s in the text:
• Check if the hash value of the pattern matches the hash value of the current substring of the text.
• If the hash values match, perform a character-by-character comparison to confirm the match.
• If a match is found, output the starting position s as the index where the pattern occurs in the text.
• Update the hash value for the next substring using a rolling hash function:
• ts+1 = (d * (ts - ASCII value of character at position s * h) + ASCII value of character at position s+m) mod q.
• Repeat this process until all positions in the text have been examined.
Output: The algorithm outputs the starting positions in the text where the pattern is found.

8. PSEUDO-CODE In this pseudo-code:
• T is the text
• P is the pattern
• d is the number of
characters in the input set.
• q is a prime number used as
modulus
• n = length[T]
• m = length[P]
• h = pow(d, m-1) mod q
• P = 0
• t0 = 0
• # Preprocessing: Compute the hash value of the pattern and the first substring of T
• for i = 1 to m
• P = (d*P + P[i]) mod q
• t0 = (d*t0 + T[i]) mod q
• # Matching: Slide the window through T and compare hash values
• for s = 0 to n-m
• if P = ts
• if P[1.....m] = T[s+1.....s+m] if s < n-m
• ts+1 = (d*(ts - T[s+1]*h) + T[s+m+1]) mod q