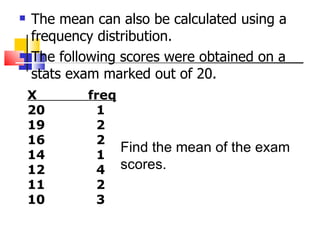
The document presents information on statistical methods and quality budgeting procedures. It discusses the five steps of quality - say what you do, do what you say, record what you do, review what you do, and restart the process. The budget is divided according to these steps, first describing measures of central tendency like mean, median and mode. It then covers measuring dispersion through tools like range, variance and standard deviation. The document reviews the processes and asks if quality is achieved or not.

1. March 2012
Statistcal
methods

2. Budget Procedure
 The Budget Will Be
Shown As A Quality
Process As The
Slides Will Be
Divided According
To The 5 Steps Of  Say What You Do
Quality.  Do What You Say
 Record What You Do
 Review What You Do
 Restart The Process

3. Say What You Do (Contents)
The Budget Shall Consist The Following
Parameters
 Need To Describe Central Tendency
 Types Of Central Tendencies
 Comparing The 3 tendencies
 Skewness Of Distribution
 Need To Measure Dispersion

4. Do What You Say &
Record What You Do
Both Steps Are Collaborated
Because recording of the Processes
shall be done side by side so as to
find the mistakes ASAP………
And Here We Present The Budget

5. Why Describe Central Tendency?
 Data often cluster around a central value
that lies between the two extremes. This
single number can describe the value of
scores in the entire data set.
 There are three measures of central
tendency.
1) Mean
2) Median
3) Mode

6. The Mode
 The mode is the most frequently occurring
number in a set of data.
• E.g., Find the mode of the following
numbers…
• 15, 20, 21, 23, 23, 23, 25, 27, 30
 Also, if there are two modes, the data set is
bimodal.
 If there are more than two modes, the data
set is said to be multimodal.

7. The Median
 The middle score when all scores in the
data set are arranged in order.
 Half the scores lie above and half lie
below the median.
 E.g., Find the median of the following
numbers…
10, 12, 14, 15, 17, 18, 20.

8.  When there are an even number of
scores, you must take the average of the
middle two scores.
Eg., 10, 12, 14, 15, 17, 18
(14 + 15)/2 = 14.5.

9.  The median can also be calculated from a
frequency distribution.
 E.g., A stats class received the following
marks out of 20 on their first exam.
X freq Cumulative
freq
20 1 15
19 2 14
16 2 12
14 1 10 What is the median grade?
12 4 9
11 2 5
10 3 3

10.  Step 1 - Multiply 0.5 times N + 1 to obtain
the location of the middle frequency.
0.5(15 + 1) = 8
 Step 2 - Locate this score on your
frequency distribution.
12

11. The Mean
 This is the sum of all the scores data set
divided by the number of scores in the set.
E.g., What’s the mean of the
∑x following test scores?
x =
n 56, 65, 75, 83, 92
x = 371/5 = 74.2

12.  The mean can also be calculated using a
frequency distribution.
 The following scores were obtained on a
stats exam marked out of 20.
X freq
20 1
19 2
16 2
Find the mean of the exam
14 1
12 4 scores.
11 2
10 3

13.  Multiply each score by the frequency. Add
them together and divide by N
X freq fX
20 1 20 X = X fX/N
19 2 38
16 2 32
14 1 14 = 204/15
12 4 48
11 2 22 = 13.6
10 3 30
N = 15 NfX = 204

14. Characteristics of the Mean
 Summed deviations about the mean equal 0.
Score X-X
2 2 - 5 = -3
3 3 - 5 = -2
5 5-5=0
7 7-5=2
__8__ 8-5=3
_ X = 25 8 (x - x) = 0
X=5

15.  The mean is sensitive to extreme scores.
Score Score Note, the median
2 2 remains the same in
3 3
both cases.
5 5
7 7
__8__ __33__
_ X = 25 _ X = 50
X=5 X = 10

16.  The sum of squared deviations is least
about the mean
Score (X - X)2
2 (2 - 5)2 = 9
3 (3 - 5)2 = 4
5 (5 - 5)2 = 0
7 (7 - 5)2 = 4
__8__ (8 - 5)2 = 9
_ X = 25 (x - x)2 =
26
X=5

17. Comparison of the Mean,
Median, and Mode
 The mode is the roughest measure of
central tendency and is rarely used in
behavioral statistics.
 Mean and median are generally more
appropriate.
 If a distribution is skewed, the mean is
pulled in the direction of the skew. In
such cases, the median is a better
measure of central tendency.

18. Skewness of Distribution
 Comparing the mean and the median
Normal Negative
Positive Skew Skew
Distribution
Mean & Median Mean Mean Median
Median the
same

19. Why Measure Dispersion?
 Measures of dispersion tell us how spread
out the scores in a data set are. Surely all
scores will not be equal to the mean.
 There are four measures of dispersion we
will look at:
• Range (crude range)
• Standard Deviation

20. The Range
 The simplest measure of variability.
Simply the highest score minus the lowest
score.
 Limited by extreme scores or outliers.
E.g., Find the range in the following test scores.
100, 74, 68, 68, 57, 56
Range = H - L = 100 - 56 = 44

21. The Variance
 The sum of the squared deviations from
the mean divided by N.
∑ (x - x)
2
s 2
=
N

22. Calculating Variance (Deviation Formula)
X X-X (X -
X)2
12 3 9
11 2 4
10 1 1
9 0 0
9 0 0
9 0 0
8 -1 1
7 -2 4
6 -3 9
∑ x = 81 ∑ (x - x) = 0 ∑ (x - x)2 =
28
x=9
S2 = ∑ (x - x)2 = 28 = 3.11
n 9

23. Calculating Standard
Deviation
 Simply calculate the square root of the
variance.
 So if s2 from the previous example was
3.11, the standard deviation (denoted
by s) is 1.76.

24. Calculating the Variance and/or
Standard Deviation
Formulae:
Variance: Standard Deviation:
s 2
=
∑( X − X ) i
2
s=
∑( X − X ) i
2
N N
Examples Are As Follows

25. Example:
Data: X = {6, 10, 5, 4, 9, 8}; N=6
Mean:
X X−X (X − X ) 2
X=
∑X =
42
=7
6 -1 1 N 6
10 3
3 9 Variance:
5 -2 4 S2 = ∑ (x - x)2 = 28 = 4.67
n 6
4 -3 9
9 2
2 4 Standard Deviation:
8 1
1 1 s = s 2 = 4.67 = 2.16
Total: 42 Total: 28

26. Review What You Do
 Need To Describe Central Tendency
 Types Of Central Tendencies
 Comparing The 3 tendencies
 Skewness Of Distribution
 Need To Measure Dispersion

27. Do We Pass The Quality Test?
No Or Yes

28. Quality Not Achieved
Please tell where we lacked and
were wrong.

29. The Process Shall Start
Again

30. Budget Ends

32. Quality Achieved

33. Budget Ends