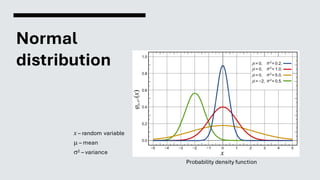
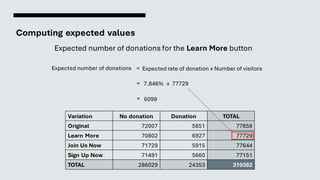
The document discusses a statistical analysis of Barack Obama's 2008 homepage, focusing on multivariate testing to measure the impact of design variations on donation conversion rates, revealing a potential increase of $60 million. It outlines the use of statistical tests, such as the chi-squared (χ2) test and t-test, to evaluate the significance of results in relation to the null hypothesis. Finally, it emphasizes the importance of using appropriate statistical methods to ensure meaningful interpretations of the data.

1. Evaluation:
Statistical
Analysis
Nuno Barreiro
Lecture 10
PC3001, PC4001, PC5001, CS2847

2. Case study
Barack Obama
homepage 2008
2

3. Multivariant
test
The originalhomepage was tested against
other designs
A text the button with three variations
• Learn More
• Join Us Now
• Sign Up Now
Five differentmedia in the placeholder
Source
https://blog.optimizely.com/2010/11/29/how-obama-raised-60-million-by-running-a-simple-experiment/

4. Goal
Measure the conversionrate of the
campaign: how many visitorsmake
donations?
Relate that conversionrate to the different
configurationsof the homepage
Select the one that attracts more donations
The estimated increasein fundraisingwas
60 million USD

5. The results
Conversion rate compared to
the original one
Conversion rate
How do we compute
this column?

6. Should the
"learn more"
button be
used?
All measurements are subject to noise: each
run of the experiment will yield different
results
We need a method to ensurethat those
measurements are meaningful
The method will indicate if the design of the
homepage should be changed

7. Testing the data
7

8. Statistical
tests
Test a statistical hypothesis
Done by comparison of the observeddata
with a data set that follows the model that is
to be tested
The comparisonis deemed statistically
significantif the relationship between the
data sets would be an unlikely realisationof
the null hypothesis
The result of the test is expressed as a
probability,the p-value

9. The null
hypothesis
H0
In a sense, the null hypothesisis the "default"
state of the world
In the case of our multivariate test, the null
hypothesissays that the modifications to the
original design don't have any impact on the
donation rate
The goal of the statistical test is to gather
evidence to reject the null hypothesis

10. The p–value
The p-value is, in future experiments, the
probability of obtaining results as "extreme"
or more "extreme" given that the null
hypothesisis true
If p = 0.05, the test suggeststhat the observeddata is inconsistentwith
the null hypothesiswith a confidence level of 95% = 1-p, which means that
the null hypothesisis rejected as very unlikely with a confidence level of 95%

11. Understanding
the p–value
The p-value is NOT the probabilityof the null
hypothesis
The rejection of the null hypothesisdoes not
tell us which of the alternatives might be the
correctone
Further tests are required to get such an
answer, although we can select the best
choice based on the results if its tendency for
improvementis clearly the best

12. 2 test
12

13. The 2 test
Compares expected values with observed
values and measures the level of variation
The number of values per variable is at least
two
Used for discretedata that follows a normal
distribution (tests of normality can be
applied to the data, but this is usually not
necessary)
We are in the conditions of applicability of the test,
provided that the data follows a normal distribution

14. Normal
distribution
 – mean
2 – variance
x – random variable
Probability density function

15. Binomial
distribution
Discrete probabilitydistribution of the
number of successesin a sequence of n
independentexperiments
Each experiment is asking a yes–no question,
each with its own Boolean-valued outcome
This distribution correspondsto A/B testing

16. Normal
distribution
facts
If the number of samples is large enough(at
least 20), the binomial distribution can be
approximated by a normal distribution
Physicalquantities that are expected to be
the sum of many independentprocesses
often have distributionsthat are nearly
normal
Averagesof random variables independently
drawn from independent
distributionsconvergein distribution to the
normal (central limit theorem)

17. Running the 2 test
17

18. The contingency
table
It's the table of occurrencefrequencies
Variation No donation Donation TOTAL
Original 72007 5851 77858
Learn More 70802 6927 77729
Join Us Now 71729 5915 77644
Sign Up Now 71491 5660 77151
TOTAL 286029 24353 310382
The sum of the last
column must be equal to
the sum of the last row
Degrees of freedom
= (nb of rows -1) * (nb of columns -1)
= (4-1) * (2-1)
= 3

19. The expected
values
Given the null hypothesis,all the variationsin
the table should have the same conversion
rate
We can compute those numbers, which
correspondto the expected values of the
experiment

20. Expected rates
The expected rates are computed from the columns totals
Variation No donation Donation TOTAL
Original 72007 5851 77858
Learn More 70802 6927 77729
Join Us Now 71729 5915 77644
Sign Up Now 71491 5660 77151
TOTAL 286029 24353 310382
Number of no donations
Number of visitors
Expected rate of no donation
286029
310382
=
= 92.154%
=
Number of donations
Number of visitors
Expected rate of donation
24353
310382
=
= 7.846%
=

21. Computing expected values
Expected number of donations for the Learn More button
Variation No donation Donation TOTAL
Original 72007 5851 77858
Learn More 70802 6927 77729
Join Us Now 71729 5915 77644
Sign Up Now 71491 5660 77151
TOTAL 286029 24353 310382
Expected rate of donation x Number of visitors
Expected number of donations
x 77729
=
= 7.846%
= 6099

22. Expected values
We repeat the processfor every variation and we get the
following table
No donation Donation
Variation Obs Exp Obs Exp
Original 72007 71749 5851 6109
Learn More 70802 71630 6927 6099
Join Us Now 71729 71552 5915 6092
Sign Up Now 71491 71098 5660 6053
Computed in the the previous slide.
The other table entries are computed in
a similar way

23. 2 computation
For each variation and each outcome (donation/no donation),
compute
Learn more no donation:
Learn more donation:
The "Learn more" contribution to the 2 is the sum of the two terms
2
learn more
(observed value – expectedvalue)2
expectedvalue
(70802 – 71630)2
71630
(6927 – 6099)2
6099
= 9.57 + 112.41 = 121.98
9.57
=
112.41
=

24. 2 computation
The value of 2 is given by
2 = 2
original + 2
learn more + 2
join us now + 2
sign up now
= 11.82 + 121.98 + 5.58 + 27.69
In our case, we have
2 = 167

25. 2 table
3 degrees of freedom correspondsto row 3
The 2 value of 167 is greater than the last cell of that row
Which means that the p-value is much smaller than 0.001
Find, in the row corresponding to the degrees of
freedom, the cell with the highest 2 value that is smaller
than the computed 2 value. The p-value of the test is in
the corresponding column.

26. Interpreting the result
The p-value is very small (less than 0.001)
The null hypothesisH0 can be rejected with a confidence
level greater than 99.9%
That's why the campaign is confidentthat one of the designs
has a chance of beating the originaldesign in terms of
conversion
In the table, we can select the design with the higher
conversionrate

27. The final
homepage

28. Statistics in
Python
SciPy (pronounced “Sigh Pie”) is a Python-
based ecosystemof open-sourcesoftware
for mathematics, science, and engineering.
It includes the package stats that offers
all the statistical tools that we need.
Import that package with the command:
import scipy.stats as stats

29. 2 test in Python
import scipy.stats as stats
a = [5851, 72007]
b = [6927, 70802]
c = [5915, 71729]
d = [5660, 71491]
obs = [a, b, c, d]
chi2, pValue, dof, expected =
stats.chi2_contingency(obs)
print 'p-value =', pValue
http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html
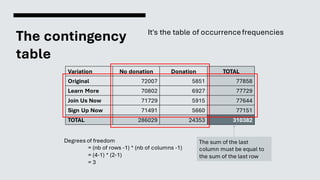
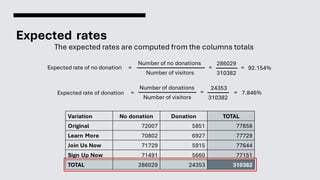
Done directly with the contingency table
No donat. Donation
5851 72007
6927 70802
5915 71729
5660 71491

30. Continuous variables
t test
30

31. Testing menu
bars
Hypothesis:Mac menu bar is faster to
access than Windows menu bar
Design: between subjects, randomised
assignment of interface to subject
Measured time in ms
Windows Mac OS
625 647
480 503
621 559
633 586
Each entry in the table
corresponds to a different
testedsubject

32. Hypothesis
testing
The hypothesiswe want to test:
position of menu bar matters
• i.e., mean(Mac times) < mean(Windows times)
The null hypothesisis:
position of menu bar makes no difference
• i.e., mean(Mac times) = mean(Windows times)

33. t test
This is a test for the null hypothesisthat 2
independentsamples have identical average
(expected) values. This test assumes that the
populations have identical variances by
default.
Compares the means of two samples
A and B
Assumptions
• Samples A and B are independent (between-
subjects, randomised)
• Normal distribution for the underlying probability
distribution of the samples
• Equal variance for both samples

34. Two versions
of the t test
Two-sided test
• H0: mean(A) = mean(B)
• H1: mean(A) != mean(B)
One-sided test
• H0: mean(A) = mean(B)
• H1: mean(A) < mean(B)
The two-sided test is more conservative,
however, if you are completely certain about
which way the differenceshould go, you can use
the one-sided test

35. Two-sided t test in
Python
import scipy.stats as stats
a = [625, 480, 621, 633]
b = [647, 503, 559, 586]
tStatistic, pValue = stats.ttest_ind(a,b)
print 'p-value =', pValue
http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html
Windows Mac OS
625 647
480 503
621 559
633 586

36. Results and
interpretation
The output from the program is
p-value = 0.7468
Can we reject the null hypothesis?

37. Paired t test
For within-subjectexperiments with two
conditions
Uses the mean of the differences(each user
againstthemselves)
For user i
• H0: mean(Ai - Bi) = 0
• H1: mean(Ai - Bi) != 0 (two-sided test)
• H1: mean(Ai - Bi) > 0 (one-sided test)
By computing the difference within each user, we’re
canceling out the contribution that’s unique to the user:
the individual differencesbetween users are no longer
contributing to the noise (variance) of the experiment
http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_rel.html

38. How to select a test
38

39. Common tests Discrete variables
• for a contingency table of size at least 2x2 with a
value of at least 5 in each cell: 2
• for any 2x2 contingencytable: Fisher's exact test
Continuous variables
• comparing two means: t test
• comparing more than two means: ANOVA (analysis
of variance)
All these tests are available in SciPy