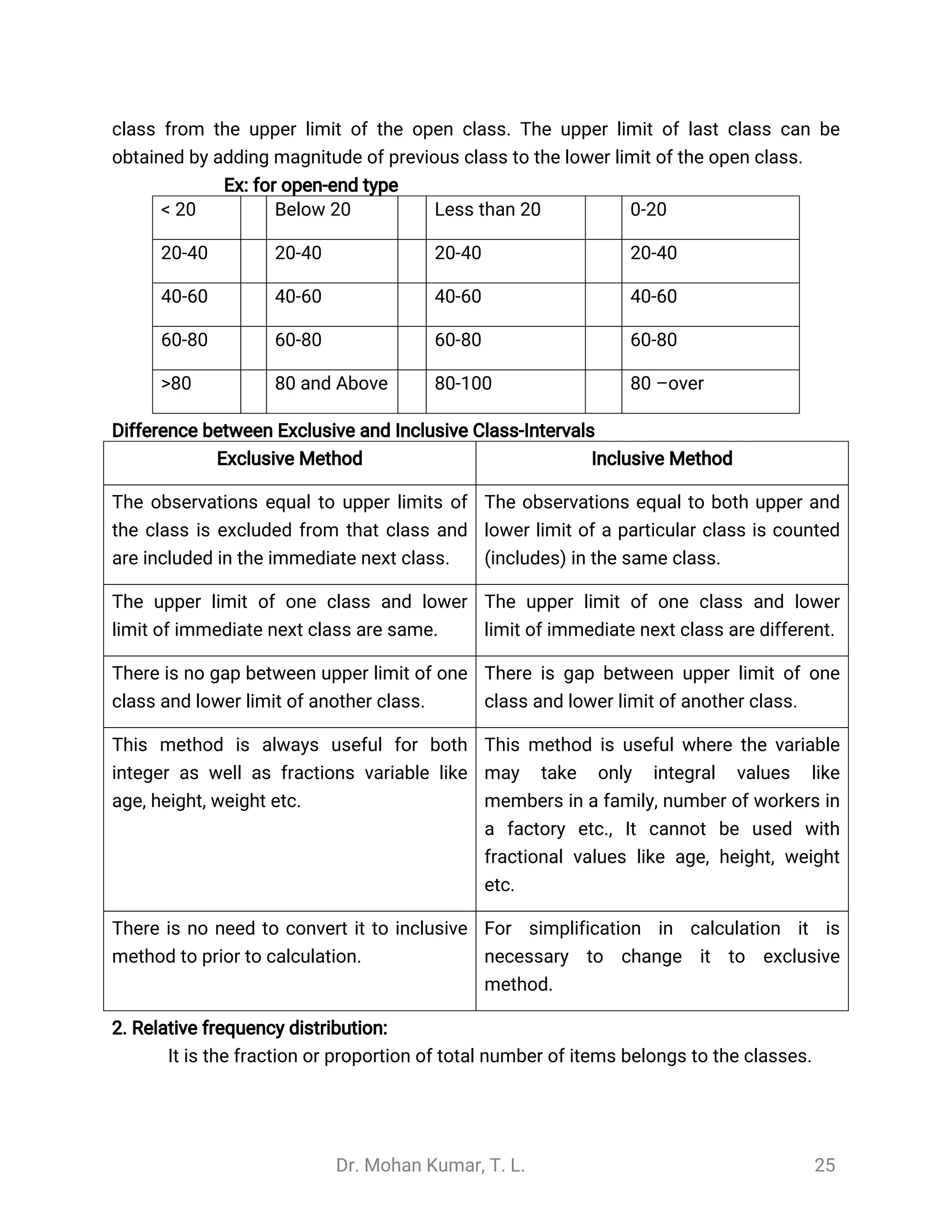
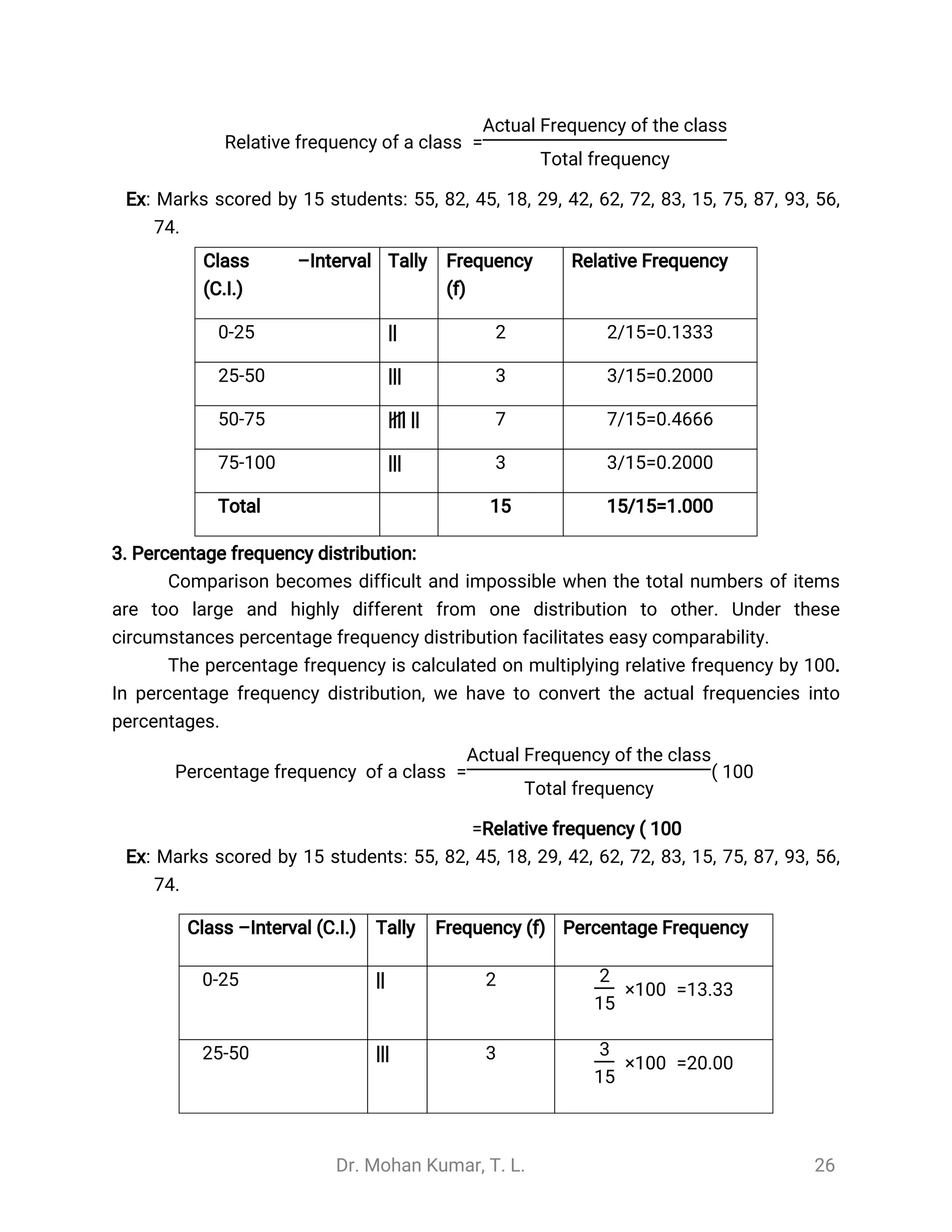
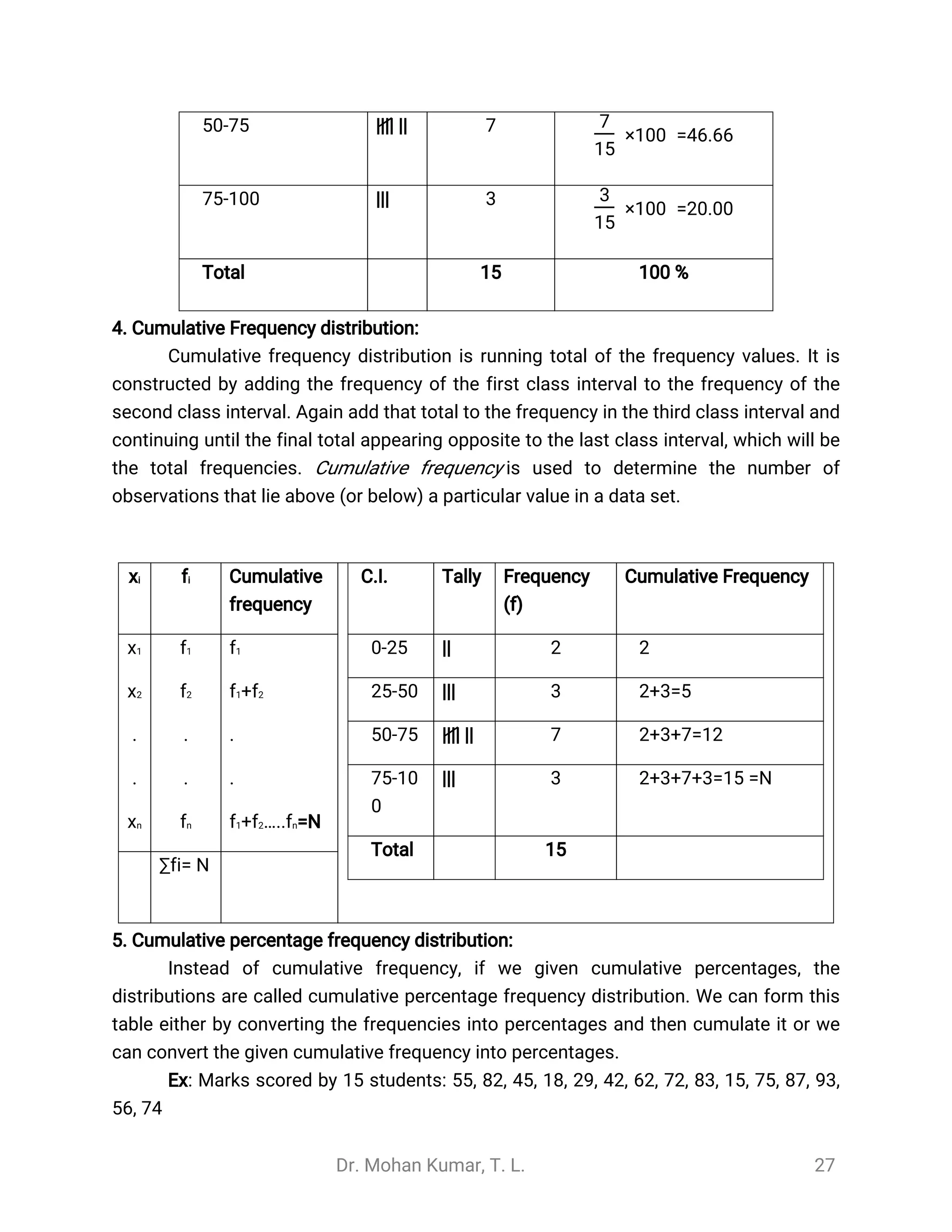
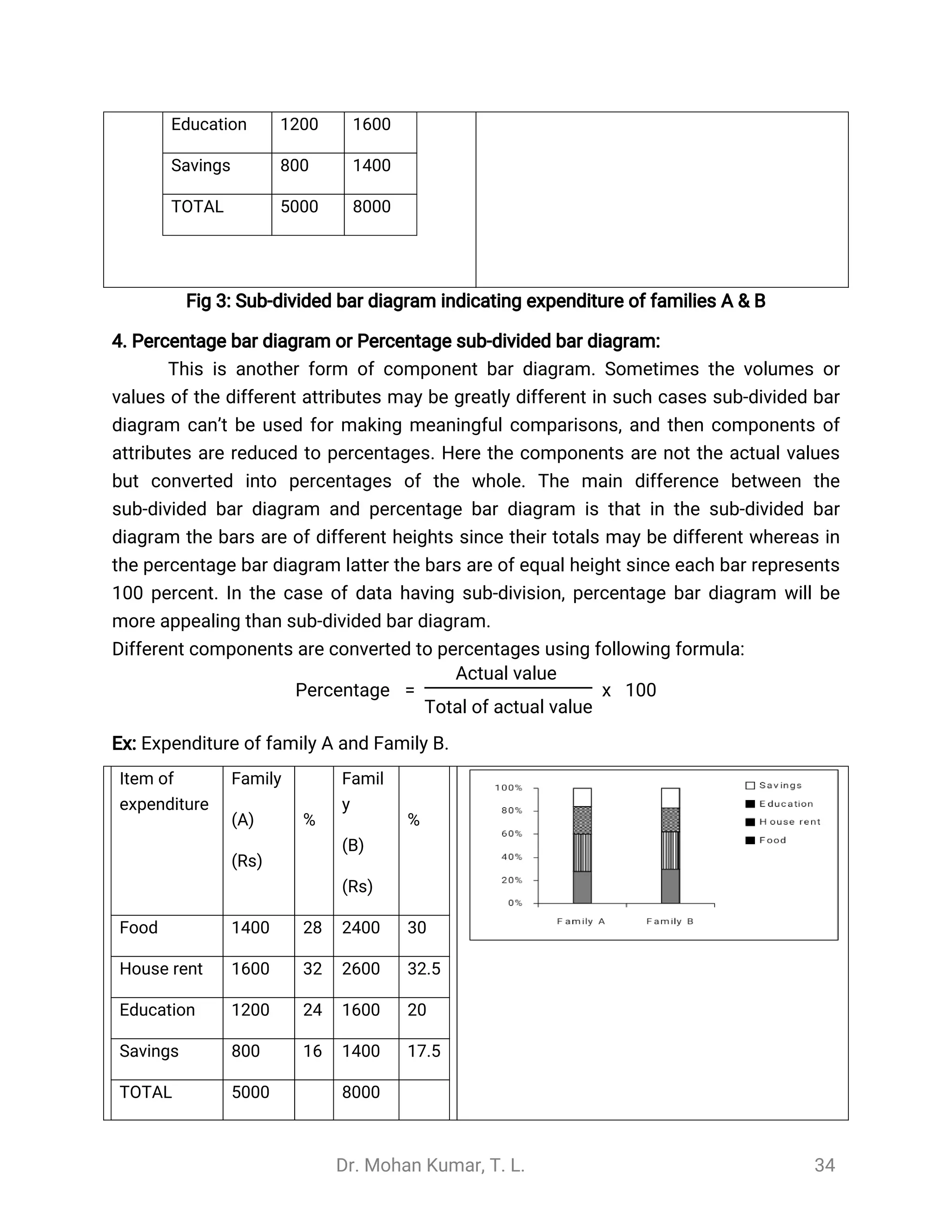
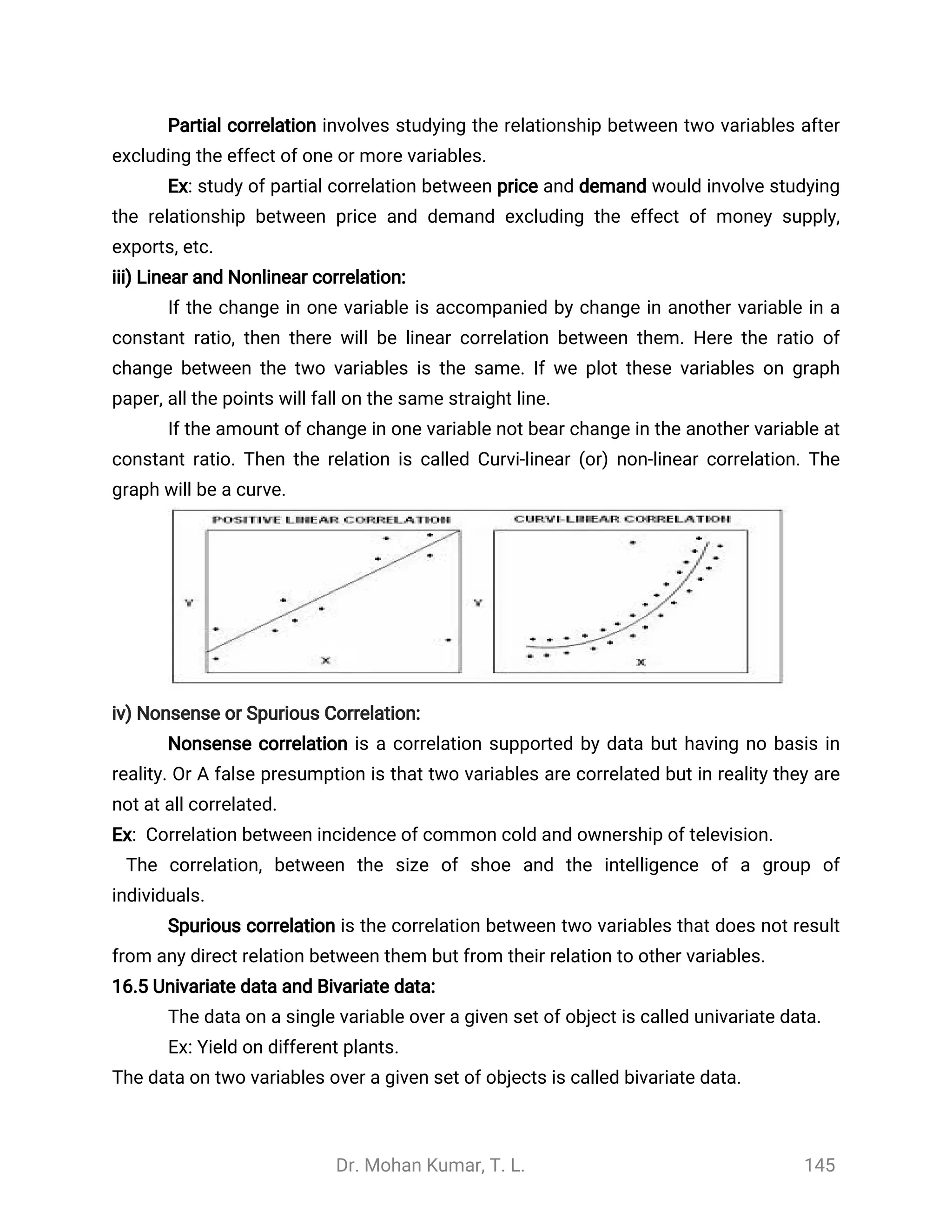
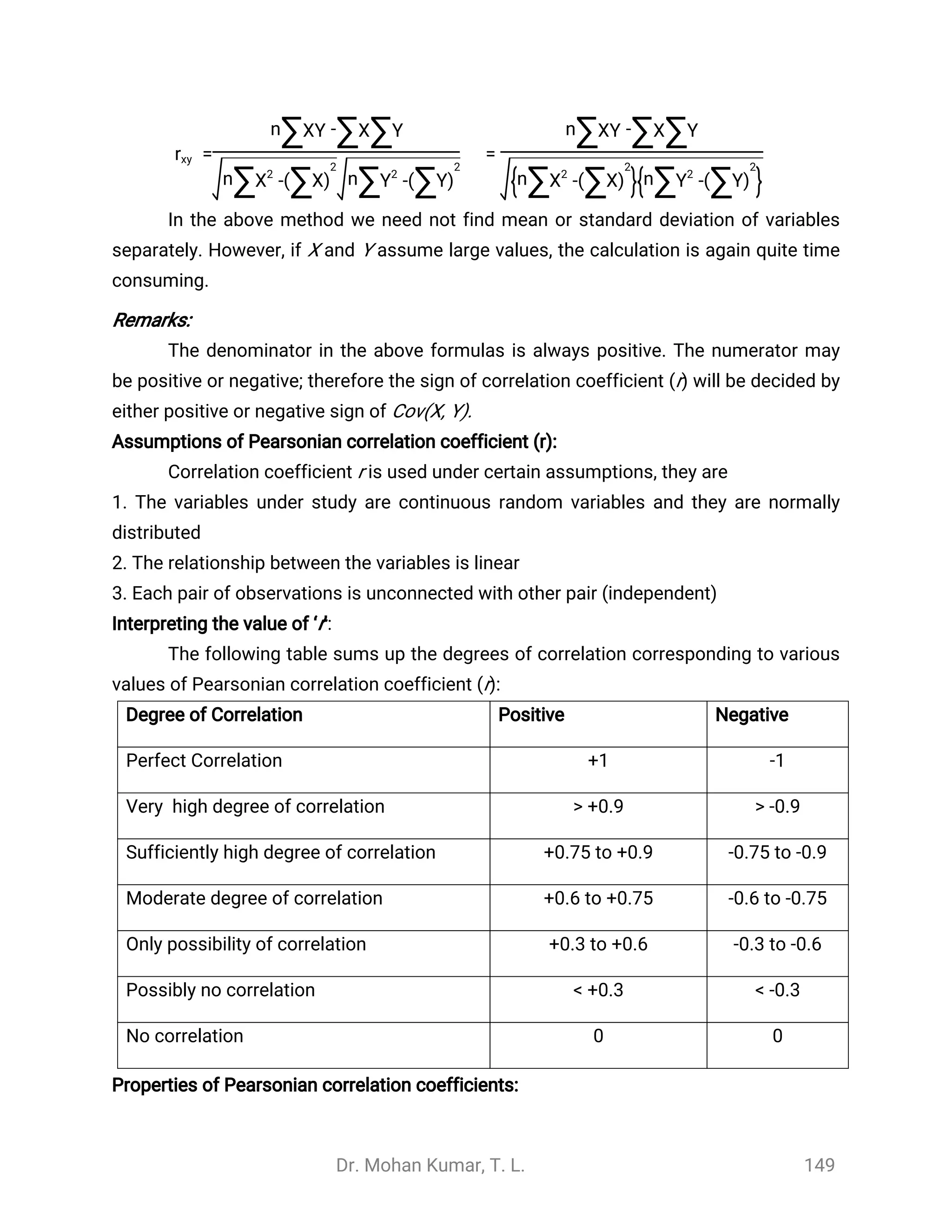
1. The document discusses the introduction to statistics, providing definitions and explaining key concepts. It describes how statistics is used in various fields like education, business, medical research, and agriculture.
2. Statistics is defined as the science of collecting, organizing, summarizing, presenting, analyzing, and interpreting data. It can be used as both a science and an art. Statistics has various applications in fields like administration, business, education, and medical and agricultural research.
3. The document outlines the basic terminology used in statistics, including data, variables, observations, quantitative and qualitative data, continuous and discrete variables. It distinguishes between primary and secondary data and their characteristics.





















































![Dr. Mohan Kumar, T. L. 58
Step1: Find cumulative frequencies (CF).
Step2: Obtain total frequency (N) and Find . Where total frequencies
N
2
N =∑n
i =1fi
Step3: See in the cumulative frequency the value first greater than value. Then the(
N
2)
th
corresponding class interval is called the Median class.
Then apply the formula given below.
Median =Md = L +
[ ( c
-c.f.
N
2
f ]
Where, L = lower limit of the median class.
N = Total frequency
f = frequency of the median class
c.f. = cumulative frequency class preceding the median class
C = width of class interval.
Graphic method for Location of median:
Median can be located with the help of the cumulative frequency curve or ‘ogive’ .
The procedure for locating median in a grouped data is as follows:
Step1: The class boundaries, where there are no gaps between consecutive classes, i.e.
exclusive class are represented on the horizontal axis (x-axis).
Step2: The cumulative frequency corresponding to different classes is plotted on the
vertical axis (y-axis) against the upper limit of the class interval (or against the
variate value in the case of a discrete series.)
Step3: The curve obtained on joining the points by means of freehand drawing is called
the ‘ogive’ . The ogive so drawn may be either a (i) less than ogive or a (ii) more
than ogive.
Step4: The value of N/2 is marked on the y-axis, where N is the total frequency.
Step5: A horizontal straight line is drawn from the point N/2 on the y-axis parallel to
x-axis to meet the ogive.
Step6: A vertical straight line is drawn from the point of intersection perpendicular to the
horizontal axis.](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-58-2048.jpg)











![Dr. Mohan Kumar, T. L. 70
Computation of Q.D.:
i) For raw data/Individual series/ ungrouped data:
Q.D. =
(Q3 - Q1)
2
Where
First quratile: =Q1 (
n +1
4 )
=3Third quratile: Q3 (
n +1
4 )
n= number of observations
ii) Frequency distribution data:
1) Discrete frequency distribution (Ungrouped frequency distribution) data:
Q.D. =
(Q3 - Q1)
2
Where
First quratile: =Q1 (
N +1
4 )
=3Third quratile: Q3 (
N +1
4 )
= Total frequencyN =∑k
i =1fi
2) Continuous frequency distribution (Grouped frequency distribution) data:
Q.D. =
(Q3 - Q1)
2
Where
First quratile: = +Q1 L1
[ x
-
N
4
m1
f1
c1]
= +Third quratile: Q3 L3
[ x
3 -
N
4
m3
f3
c3]
Where, & = lower limit of the first & third quartile class.L1 L3
= Total frequencyN =∑k
i =1fi](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-70-2048.jpg)



























































![Dr. Mohan Kumar, T. L. 130
Chapter 15: Small Sample Tests:
15.1 Introductions:
The entire large sample theory was based on the application of “Normal test”.
The normal tests are based upon important assumptions of normality. But the
assumptions of normality do not hold good in the theory of small samples. If the
sample size “n” is small, the distribution of the various statistics (Z tests) are far from
normality and as such “Normal test” cannot be applied. Thus, a new technique is
needed to deal with the theory of small samples.
If the sample size is less than 30 (n < 30), then it is called small sample. For small
samples (n<30) generally we apply Student’s‘t’ test, ‘F-test and ‘Chi-square test’.
Independent Sample:
Two samples are said to be independent if the sample selected from one
population is not related to the sample selected from the second population.
Ex: a) Systolic blood pressures of 30 adult females and 30 adult males.
b) The yield samples from two varieties.
c) The soil samples are taken at different locations.
Dependent Sample:
Two samples are said to be dependent if each member of one sample corresponds
to a member of the other sample or if the observations in two samples are related.
Dependent samples are also called paired samples or matched samples.
Ex: a) The samples of nitrogen uptake by the top leaves and bottom
b) The yield samples from one variety before application of fertilizer and after
application of fertilizer.
c) Midterm and Final exam scores of 10 Statistic students.
Degrees of Freedom (df):
The number of independent variates which make up the statistic is known as the
degrees of freedom. Or
Degrees of freedom is defined as number of observations in a set minus number
of restrictions imposed on it. It is denoted by ‘df ‘
Suppose it is asked to write any four numbers then one will have all the numbers
of his choice. If a restriction is imposed to the choice is that the sum of these numbers
should be 50. Here, we have a choice to select any three numbers, say 10, 15, 20 and
the fourth number should be is 5 in order to make sum equals to 50: [50 - (10 +15+20)].](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-130-2048.jpg)




![Dr. Mohan Kumar, T. L. 135
Steps:
1. H0: µ1 = µ2
H1: µ1 ≠ µ2
2. Level of significance (α) = 5% or 1%
3. Consider test statistic: under H0
t = ~ df
⃓ ⃓
̅
d
s
n
t(n -1)
where, ; di=(xi-yi) = difference between paired observations and=
̅
d
∑di
n
S = 1
n -1[ -∑d2
( ∑d)
2
n ]
4. Compare the ‘tcal’ calculated value with the ‘ttab’ table value for (n-1) df at α level of
significance.
5. Determination of Significance and Decision
a. If |t cal| ≥ t tab for (n-1) df at α, Reject H0.
b. If |t cal| < t tab for (n-1) df at α, Accept H0.
6. Conclusion
a. If we reject the null hypothesis H0 conclusion will be there is significant difference
between the two sample means.
b. If we accept the null hypothesis H0 conclusion will be there no is a significant
difference between the two sample means.
15.6 Chi- Square Test ( test):χ2
The various tests of significance such that as Z-test, t-test, F-test have mostly
applicable to only quantitative data and based on the assumption that the samples were
drawn from normal population. Under this assumption the various statistics were
normally distributed. Since the procedure of testing the significance requires the
knowledge about the type of population or parameters of population from which
random samples have been drawn, these tests are known as parametric tests.
But there are many practical situations the assumption of about the distribution
of population or its parameter is not possible to make. The alternative technique where
no assumption about the distribution or about parameters of population is made are
known as non-parametric tests. Chi-square test is an example of the non-parametric](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-135-2048.jpg)
![Dr. Mohan Kumar, T. L. 136
test and distribution free test.
Definition:
The Chi- square ( ) test (Chi-pronounced as ki) is one of the simplest and mostχ2
widely used non-parametric tests in statistical work. The test was first used by Karlχ2
Pearson in the year 1900. The quantity describes the magnitude of the discrepancyχ2
between theory and observation. It is defined as
= ~ dfχ2
∑[
( -oi Ei)2
Ei
] χ2
(n)
Where ‘O’ refers to the observed frequencies and ‘E’ refers to the expected frequencies.
Remarks:
1) If is zero, it means that the observed and expected frequencies coincide with eachχ2
other. The greater the discrepancy between the observed and expected frequencies the
greater is the value of .χ2
2) -test depends on only the on the set of observed and expected frequencies and on.χ2
degrees of freedom (df), it does not make any assumption regarding the parent
population from which the observation are drawn and it test statistic does not involves
any population parameter, it is termed as non-parametric test and distribution free test.
Measuremental data: The data obtained by actual measurement is called
measuremental data. For example, height, weight, age, income, area etc.,
Enumeration data: The data obtained by enumeration or counting is called enumeration
data. For example, number of blue flowers, number of intelligent boys, number of curled
leaves, etc.,
– test is used for enumeration data which generally relate to discrete variable whereχ2
as t-test and standard normal deviate tests are used for measure mental data which
generally relate to continuous variable.
Properties of Chi-square distribution:
1. The mean of distribution is equal to the number of degrees of freedom (n)χ2
2. The variance of distribution is equal to 2nχ2
3. The median of distribution divides, the area of the curve into two equal parts, eachχ2
part being 0.5.
4. The mode of distribution is equal to (n-2)χ2
5. Since Chi-square values always positive, the Chi square curve is always positively
skewed.](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-136-2048.jpg)

![Dr. Mohan Kumar, T. L. 138
= ~χ2
n
∑i =1
[
( -oi Ei)2
Ei
] χ2
df(υ =n -k -1)
Follows -distribution with υ= n – k – 1 d.f. where O1, O2, ...On are the observedχ2
frequencies, E1 , E2…En, corresponding to the expected frequencies and k is the number
of parameters to be estimated from the given data. A test is done by comparing the
computed value with the table value of for the desired degrees of freedom.χ2
2. To test the independence of attributes - for m x n Contingency Table.
Let us consider the two attributes A and B, A is divided into m classes A1, A2, A3,...,
Am and B is divided into n classes B1, B2, B3,..., Bn. such a classification in which attributes
are divided into more than two classes is known as manifold classification. The various
cell frequencies can be expressed in the following table know as m*n manifold
contingency table. Where Oij denoted the cell which represents the number of person
possessing the both attributes Ai and Bj (i=1,2,3...,m; j=1,2,3...,n). Ri and Cj are
respectively called as ith
row total and jth
columns total (i=1,2,3..m and j=1,2,3..n) which
are called as marginal totals, and N is grand total.
Table 1: mxn Contingency table
Attribute
B
Attribute A
Row
Total
B1 B2 B3 .....
.
Am
A1 O11 O12 O13 ... Om3 R1
A2 O21 O22 O23 .... Om3 R2
A3 O31 O33 O33 ... Om3 R3
.
.
.
.
.
.
.
.
.
...
.
.
...
.
.
Am On1 On2 On3 Omn Rn
Col Total C1 C2 C3 .... Cm N](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-138-2048.jpg)

![Dr. Mohan Kumar, T. L. 140
B2 C d (c+d)= R2
Col Total (a+c)=C1 (b+d )=C2 a+b+c+d= N
The formula for finding from the observed frequencies a,b,c and d isχ2
= ~χ2
N(ad -bc)2
((c +d)(a +c)(b +d)(a +b)
χ2
1 df
The decision about independence of factor/attributes A and B is taken by comparing
with at certain level of significance; We reject or accept the null hypothesiscalχ2
tabχ2
accordingly at that level of significance.
Yate’ s Correction for Continuity
In a 2´2 contingency table, the number of df is (2-1)(2-1) =1. If any one of the
theoretical cell frequency is less than 5, the use of pooling method will result in df = 0
which is meaningless. In this case we apply a correction given by F. Yate (1934) which
is usually known as “Yates correction for continuity”. This consisting adding 0.5 to cell
frequency which is less than 5 and then adjusting for the remaining cell frequencies
accordingly. Thus corrected values of is given asχ2
=χ2
N[ -N/2]|ad -bc| 2
((c +d)(a +c)(b +d)(a +b)
F – Statistic Definition:
If X is a variate with n1 df and Y is an independent - variate with n2 df, then F- statisticχ2
χ2
is defined as i.e. F - statistic is the ratio of two independent chi-square variates divided
by their respective degrees of freedom. This statistic follows G.W. Snedocor’s
F-distribution with ( n1, n2) df i.e. F = ~
X
n1
Y
n2
F df(n1, n2)
Application of F-test:
1 Testing Equality/homogeneity of two population variances.
2 Testing of Significance of Equality of several means.
3 Testing of Significance of observed multiple correlation coefficients.
4 Testing of Significance of observed sample correlation ratio.
5 Testing of linearity of regression
1) Testing the Equality/homogeneity of two population variances:
Suppose we are interested to test whether the two normal populations have](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-140-2048.jpg)
























![Dr. Mohan Kumar, T. L. 168
significant difference betweenvarieties ( breeds)
2. Level of significance ((): 5% or 1%
3. Test Statistic:
1) Find the sum of values of all n (=k(h) items of the given data.
Let this grand total represented by ‘GT ’.
Then correction factor (C.F.) =
(GT)2
N
2) Find the total sum of squares (TSS) TSS = -(C.F.)∑k
i =1∑h
j =1
y2
ij
3) Find the sum of squares between treatments or sum of squares between rows is
SSTr =SSR = -∑k
i =1
R2
i
h
(C.F.)
where ‘h’ is the number of observations in each row
4) Find the sum of squares between varieties or sum of squares between columns
is
SSVt =SSC = -∑h
j =1
C2
j
k
(C.F.)
where ‘k’ is the number of observations in each column.
5) Find the sum of squares due to error by subtraction: SSE = TSS - SSR - SSC
ANOVA TABLE
Sources of Variation d.f. Sum of
squares
(S.S.)
M.S.S F ratio
Between Treatments k-1 SSTr MST= SST/k-1 FT=MST/ MSE
Between Varieties h-1 SSVt MSV=SSV/h-1 FV=MSV/ MSE
Within treatment and
varieties (Error)
(k-1)(h-
1)
SSE MSE= SSE/N-k
Total n-1 TSS
4 Critical values of F table (Ftab):
(i) For comparison between treatments, obtain F-table value for [k-1, (k-1) (h-1)] df at (
level of significance and denoted it as Ftab.
(ii) For comparison between Varieties, obtain F-table value for [k-1, (k-1) (h-1)] df at (
level of significance and denoted it as Ftab.
5. Decision criteria.
(i) If FT ≥ Ftab for [k-1, (k-1) (h-1)] df at ( level of significance, H0 is rejected.](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-168-2048.jpg)
![Dr. Mohan Kumar, T. L. 169
(ii) If FV ≥ Ftab for [h-1, (k-1) (h-1)] df at ( level of significance, H0 is rejected.](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-169-2048.jpg)












![Dr. Mohan Kumar, T. L. 182
a) If F cal < F tab then F is not significant. We can conclude that there is no significant
difference between replications. It indicates that the RBD will not contribute to
precision in detecting treatment differences. In such situations the adoption of RBD
in preference to CRD is not advantageous.
b) If F cal ≥ F tab then F is significant. It indicates there is a significant difference between
replications. In such situations the adoption of RBD in preference to CRD is advantages.
Then to know which of the treatment means are significantly different, we
will use Critical Difference (CD).
CD = * SE (d)tα, edf
Where, → table ‘t’ value for error df at α level of significancetα, edf
t = number of treatment]SE =(d)
2EMS
t
7) Advantages of RBD
1) The precision is more in RBD.
2) The amount of information obtained in RBD is more as compared to CRD.
3) RBD is more flexible.
4) Statistical analysis is simple and easy.
5) Even if some values are missing, still the analysis can be done by using missing
plot technique.
6) It uses all the basic principles of experimental designs.
7) It can be applied to field experiments.
8) Disadvantages of RBD
1) When the number of treatments is increased, the block size will increase. If the
block size is large, maintaining homogeneity is difficult. When more number of
treatments is present in the experiment this design may not be suitable.
2) It provides smaller df to experimental error as compared to CRD.
3) If there are many missing data, RCBD experiment may be less efficient than a CRD
9) Uses of RBD: RBD is more useful under the following conditions
1) Most commonly and widely used design in field experiments.
2) When the experimental materials have heterogeneity only in one direction i.e.
There is only one source of variation in the experimental material.](https://image.slidesharecdn.com/statisticnote-190125155739/75/Statistic-note-182-2048.jpg)
