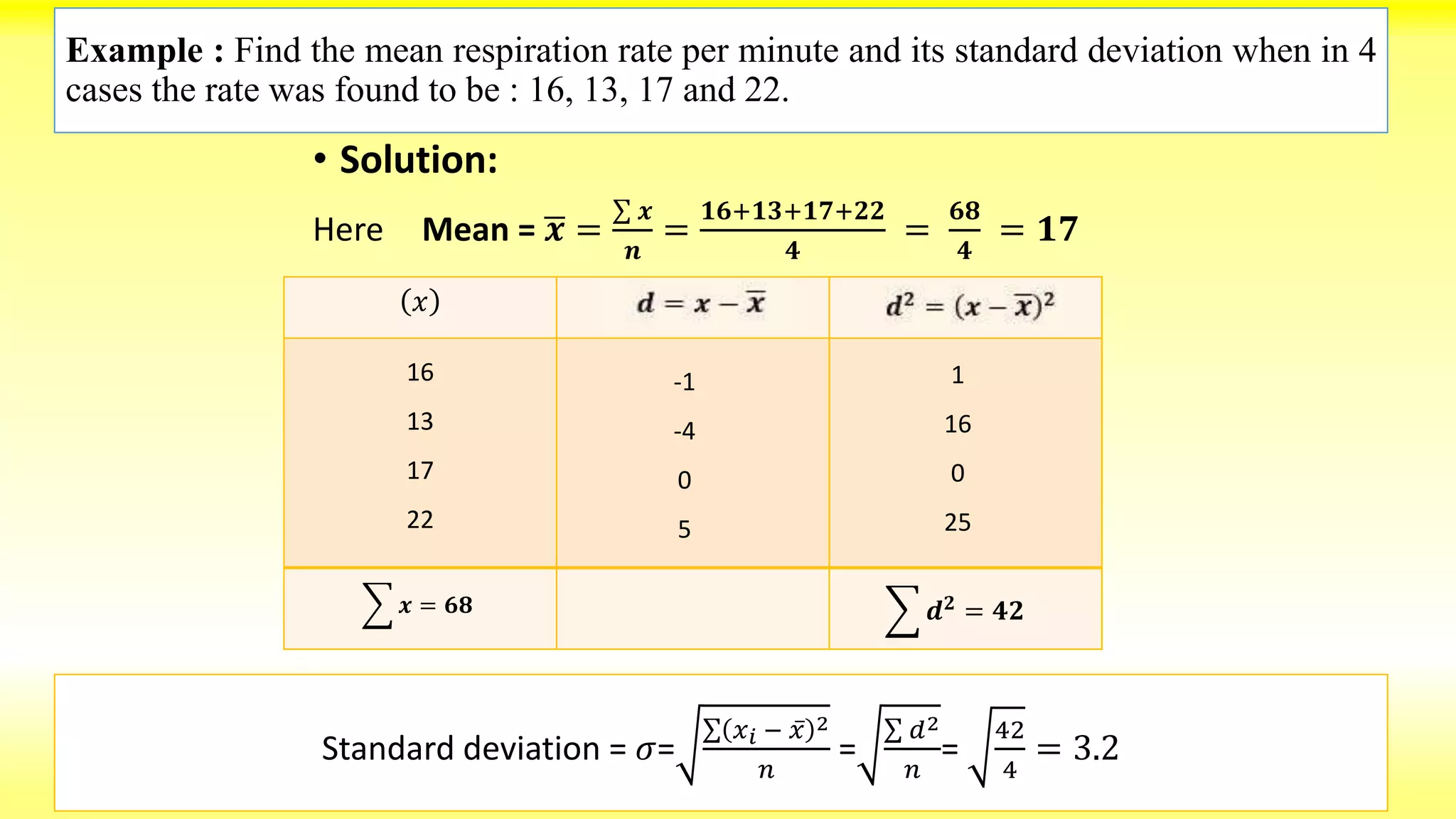
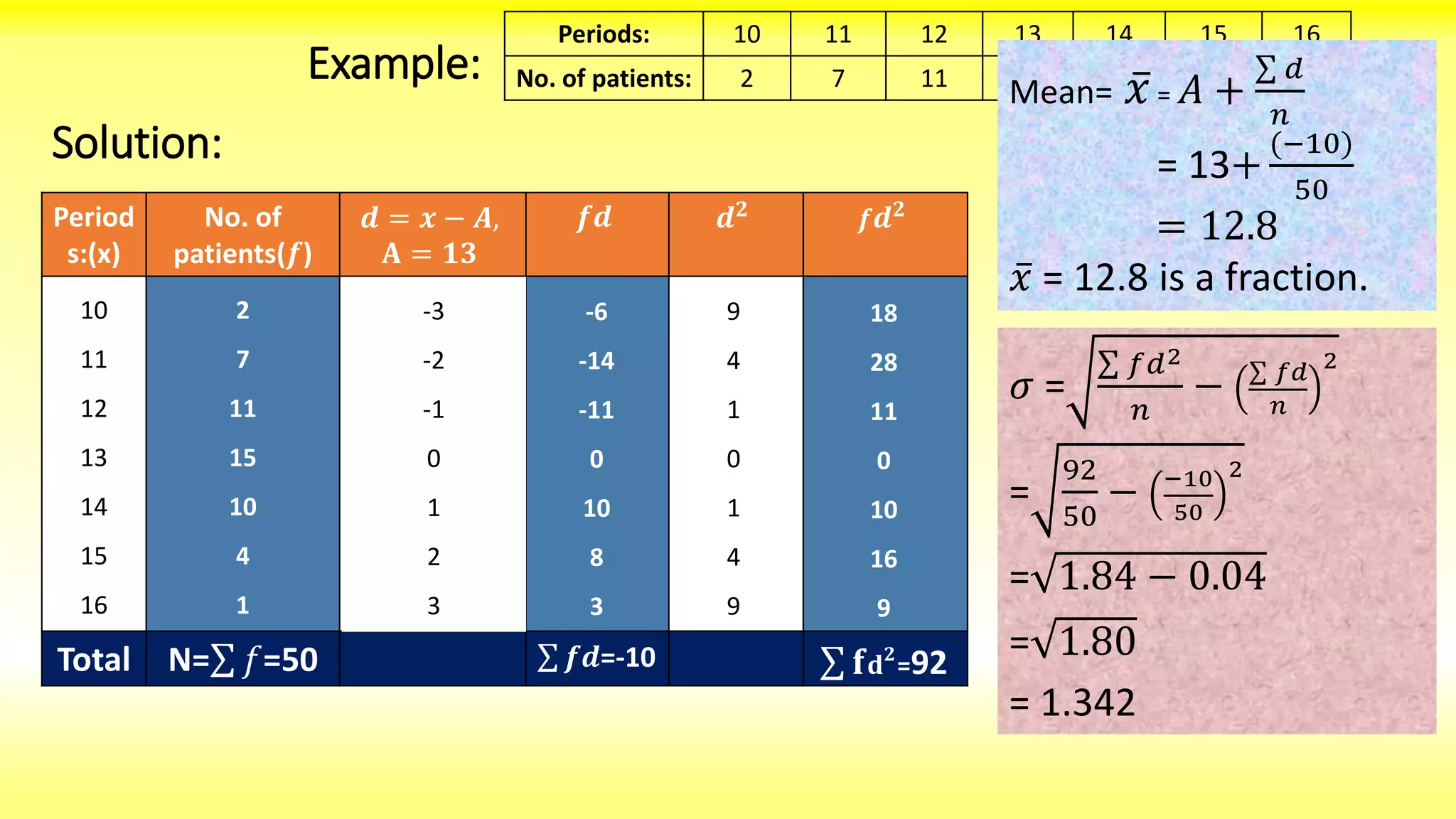
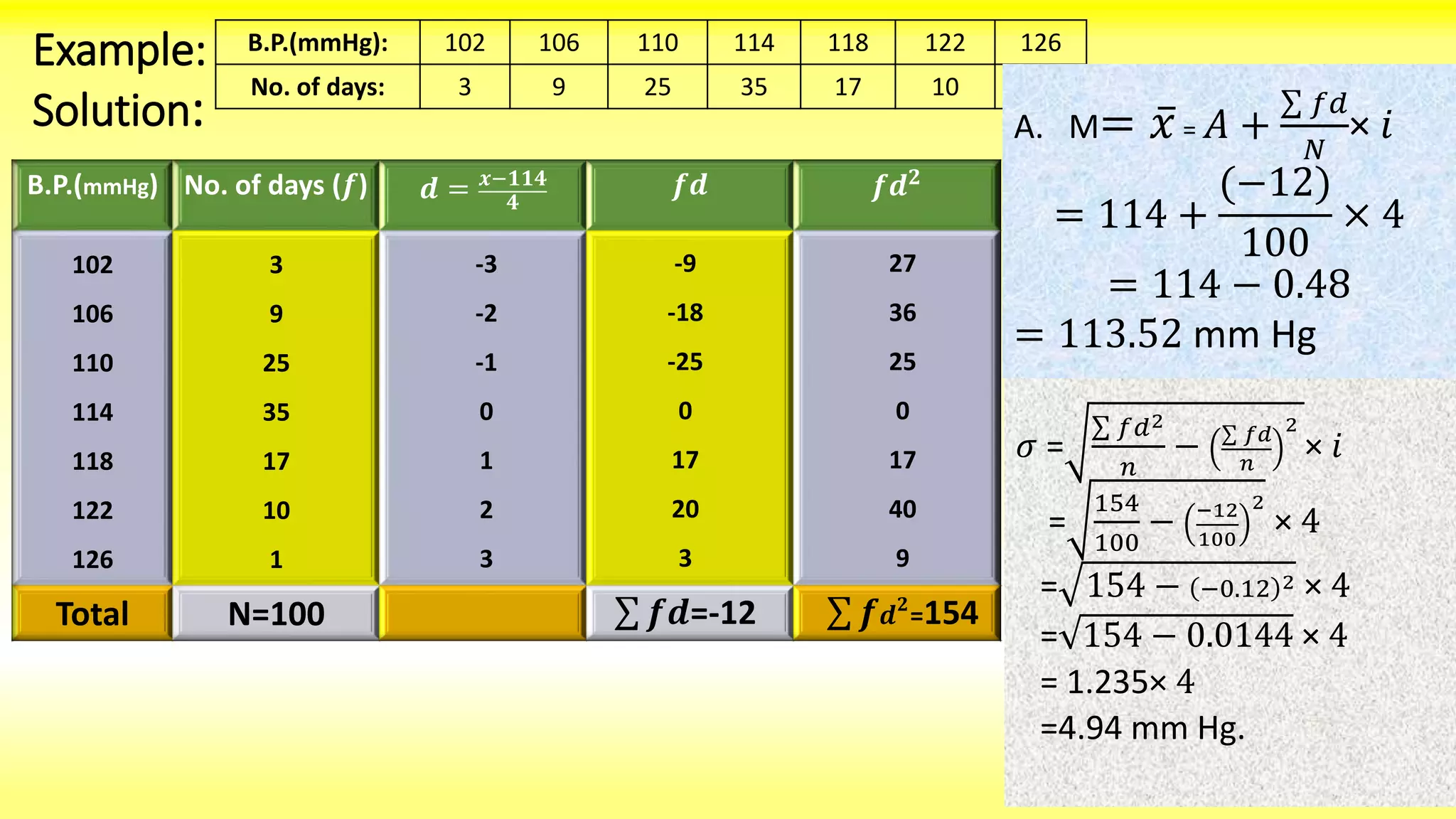
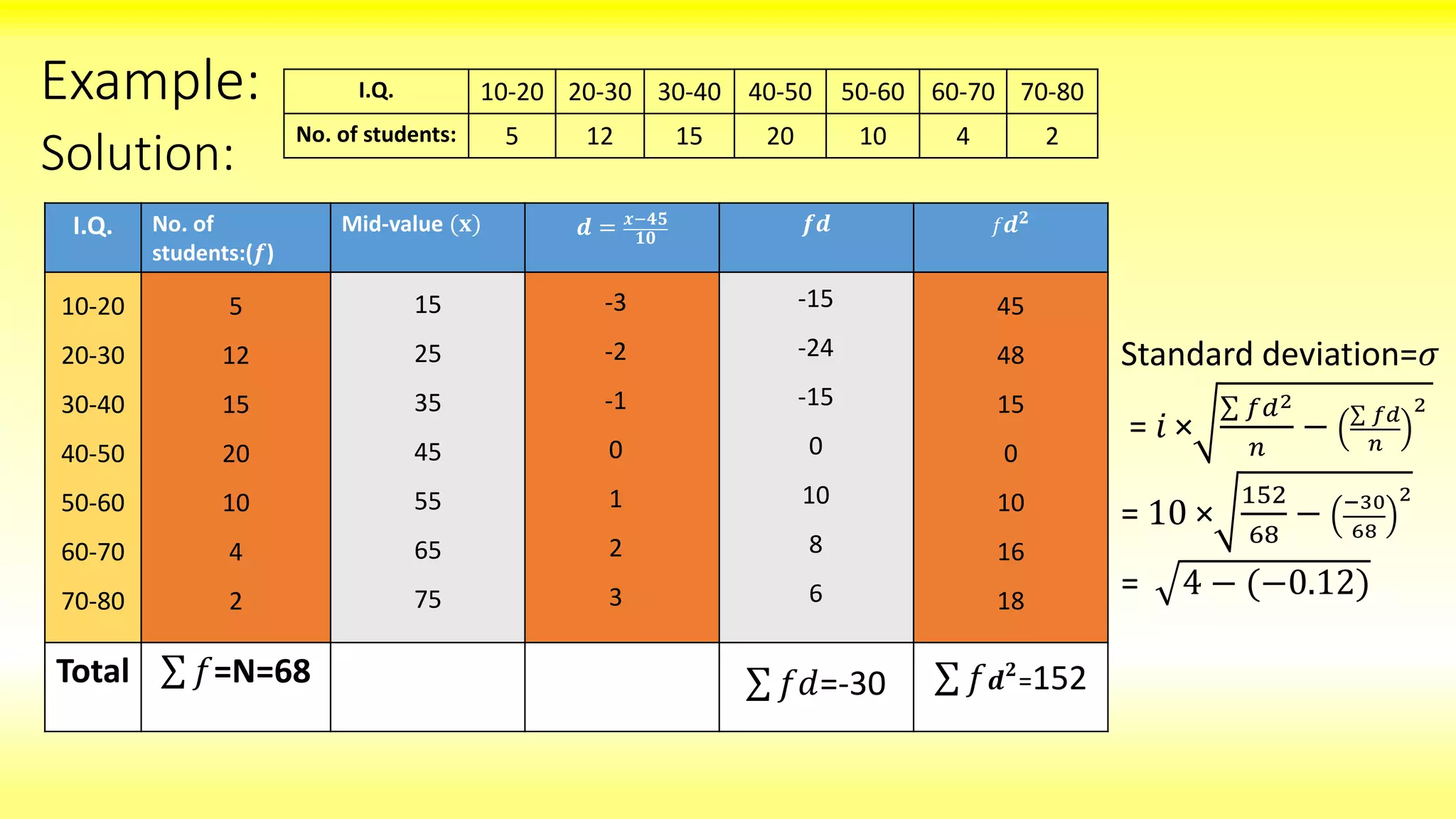
The seminar presented by Jiban Ku Singh at Berhampur University details the standard deviation as a key measure of dispersion introduced by Karl Pearson. It explains its calculation methods, including direct and shortcut methods, and compares it with other measures of dispersion like range and quartile deviation. The document highlights the merits and demerits of standard deviation, emphasizing its scientific importance and widespread application in statistics.

1. Seminar on
Standard Deviation
Presented by:
Jiban Ku. Singh
M. Sc Part-I (2015-16)
P. G. DEPARTMENT OF BOTANY
BERHAMPUR UNIVERSITY
BHANJA BIHAR, BERHAMPUR- 760007
GANJAM, ODISHA, INDIA
E-mail- jibansingh9@gmail.com

2. Mean
Median
Mode
Quartile deviation

3. Standard Deviation
• While looking at the earlier measures of dispersion all of them suffer
from one or the other demerit i.e.
• Range –it suffer from a serious drawback considers only 2 values and
neglects all the other values of the series.
• Quartile deviation considers only 50% of the item and ignores the
other 50% of items in the series.
• Mean deviation no doubt an improved measure but ignores negative
signs without any basis.
3

4. Standard Deviation
• The concept of standard deviation was first introduced by Karl Pearson in
1893.
• Karl Pearson after observing all these things has given us a more scientific
formula for calculating or measuring dispersion. While calculating SD we
take deviations of individual observations from their AM and then
each squares. The sum of the squares is divided by the Total number of
observations. The square root of this sum is knows as standard
deviation.
• The standard deviation is the most useful and the most popular measure of
dispersion.
• It is always calculated from the arithmetic mean, median and mode is not
considered.
4

5. Definition:
• Standard Deviation is the positive square root of the average of squared
deviation taken from arithmetic mean.
• The standard deviation is represented by the Greek letter 𝝈(sigma).
• Formula.
• Standard deviation = 𝜎=
𝑥− 𝑥 2
𝑛

6. • Standard deviation = 𝜎 =
𝑥− 𝑥 2
𝑛
• Alternatively 𝜎 =
𝑥2
𝑛
− 𝑥
𝑛
2
=
𝒙 𝟐 − 𝟐𝒙 𝒙 + 𝒙 𝟐
𝒏
=
𝒙 𝟐
𝒏
− 𝟐 𝒙
𝒙
𝒏
+
𝒙 𝟐
𝒏
=
𝒙 𝟐
𝒏
− 𝟐 𝒙 𝒙 +
𝐧 𝒙 𝟐
𝒏
=
𝒙 𝟐
𝒏
− 𝟐 𝒙 𝟐 + 𝒙 𝟐
=
𝒙 𝟐
𝒏
− 𝒙 𝟐

7. CALCULATION OF STANDARD DEVIATION-
INDIVIDUAL OBSERVATION
Two Methods:-
By taking deviation of the items from the actual mean.
By taking deviation of the items from an assumed mean.

8. CASE-I. When the deviation are taken from the actual mean.
DIRECT METHOD
Standard deviation = 𝜎=
𝑥 𝑖 − 𝑥 2
𝑛
or =
𝑑2
𝑛
𝑤ℎ𝑒𝑟𝑒 𝑑 = 𝑥𝑖 − 𝑥
𝑥𝑖=value of the variable of observation,
𝑥= arithmetic mean
𝑛= total number of observations.

9. Example : Find the mean respiration rate per minute and its standard deviation when in 4
cases the rate was found to be : 16, 13, 17 and 22.
• Solution:
Here Mean = 𝒙 =
𝒙
𝒏
=
𝟏𝟔+𝟏𝟑+𝟏𝟕+𝟐𝟐
𝟒
=
𝟔𝟖
𝟒
= 𝟏𝟕
𝑥
16
13
17
22
𝒙 = 𝟔𝟖
Standard deviation = 𝜎=
𝑥 𝑖 − 𝑥 2
𝑛
=
𝑑2
𝑛
=
42
4
= 3.2
-1
-4
0
5
1
16
0
25
𝒅 𝟐
= 𝟒𝟐

10. Short-Cut Method
Standard deviation = 𝜎=
𝑑2
𝑛
−
𝑑
𝑛
2
𝑤ℎ𝑒𝑟𝑒 𝑑 = 𝑥 − 𝐴, 𝐴 = 𝑎𝑠𝑠𝑢𝑚𝑒𝑑 𝑚𝑒𝑎𝑛,
𝑛 = 𝑡𝑜𝑡𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛.
CASE-II. When the deviation are taken from the Assumed mean.

11. 𝑆. 𝐷 = 𝜎=
𝑑2
𝑛
−
𝑑
𝑛
2
=
2689
10
− 1
10
2
= 268.9 − 0.01
= 268.89
= 16.398
Example: Blood serum cholesterol levels of 10 persons are as under:
240, 260, 290, 245, 255, 288, 272, 263, 277, 251.
calculation standard deviation with the help of assumed mean.
Value 𝒙 𝒅 = 𝒙 − 𝑨
A=264
240
260
290
245
255
288
272
263
277
251
𝒏 = 𝟏𝟎
𝒅 𝟐
576
16
676
361
81
576
64
1
169
169
𝒅 𝟐
= 𝟐𝟔𝟖𝟗
-24
-4
26
-19
-9
24
8
-1
13
13
d = 1
Here,
Mean= 𝑥 = 𝐴 +
𝑑
𝑛
= 264 +
(1)
10
= 263.9
𝑥 = 263.9 is a fraction.

12. CALCULATION OF STANDARD DEVIATION- DISCERETE SERIES OR
GROUPED DATA
Three Methods
a)Actual Mean Method or Direct Method
b)Assumed Mean Method or Short-cut Method
c)Step Deviation Method

13. a) Actual Mean Method or Direct Method
• The S.D. for the discrete series is given by the formula.
𝜎=
𝑓 𝑥 − 𝑥 2
𝑛
Where 𝑥 is the arithmetic mean,
𝑥 is the size of items,
𝑓 is the corresponding frequency
and 𝑛 = 𝑓

14. b) Assumed Mean Method or Short-cut Method
Standard deviation=𝜎 =
𝑓𝑑2
𝑛
− 𝑓𝑑
𝑛
2
Where 𝐴 is the assumed mean,
𝑑 = 𝑥 − 𝐴
𝑓 is the corresponding frequency
and 𝑛 = 𝑓

15. Example:
Periods: 10 11 12 13 14 15 16
No. of patients: 2 7 11 15 10 4 1
Solution:
Period
s:(x)
No. of
patients(𝒇)
𝒅 = 𝒙 − 𝑨,
𝐀 = 𝟏𝟑
𝒇𝒅 𝒅 𝟐
𝒇 𝒅 𝟐
10
11
12
13
14
15
16
2
7
11
15
10
4
1
Total N= 𝑓=50
-3
-2
-1
0
1
2
3
-6
-14
-11
0
10
8
3
𝒇𝒅=-10
9
4
1
0
1
4
9
18
28
11
0
10
16
9
𝐟 𝐝 𝟐
=92
Mean= 𝑥 = 𝐴 +
𝑑
𝑛
= 13+
(−10)
50
= 12.8
𝑥 = 12.8 is a fraction.
𝜎 =
𝑓𝑑2
𝑛
− 𝑓𝑑
𝑛
2
=
92
50
− −10
50
2
= 1.84 − 0.04
= 1.80
= 1.342

16. c) Step Deviation Method
• We divide the deviation by a common class interval and use the
following formula
Standard deviation=𝜎 =
𝑓𝑑2
𝑛
− 𝑓𝑑
𝑛
2
× 𝑖
Where 𝑖 = common class interval,
𝑑 = 𝒙−𝑨
𝒊 ,
𝐴 = is assumed mean
𝑓 = f is the respective frequency.

17. 𝜎 =
𝑓𝑑2
𝑛
− 𝑓𝑑
𝑛
2
× 𝑖
=
154
100
− −12
100
2
× 4
= 154 − −0.12 2 × 4
= 154 − 0.0144 × 4
= 1.235× 4
=4.94 mm Hg.
Example: B.P.(mmHg): 102 106 110 114 118 122 126
No. of days: 3 9 25 35 17 10 1
Solution:
B.P.(mmHg) No. of days (𝒇) 𝒅 = 𝒙−𝟏𝟏𝟒
𝟒
𝒇𝒅 𝒇𝒅 𝟐
102
106
110
114
118
122
126
3
9
25
35
17
10
1
Total N=100
-3
-2
-1
0
1
2
3
-9
-18
-25
0
17
20
3
𝒇𝒅=-12
27
36
25
0
17
40
9
𝒇 𝒅 𝟐
=154
A. M= 𝑥 = 𝐴 +
𝑓𝑑
𝑁
× 𝑖
= 114 +
(−12)
100
× 4
= 114 − 0.48
= 113.52 mm Hg

18. S.D. of Continues Series can be calculated by any one of the methods discussed
for discrete frequency distribution But Step Deviation Method is mostly used.
Standard deviation=𝜎 =
𝑓𝑑2
𝑛
− 𝑓𝑑
𝑛
2
× 𝑖
Where𝑖 = common class interval,
𝑑 = 𝒙−𝑨
𝒊
,
𝐴 = is assumed mean
𝑓 = f is the respective frequency.

19. Example: I.Q. 10-20 20-30 30-40 40-50 50-60 60-70 70-80
No. of students: 5 12 15 20 10 4 2
Solution:
I.Q. No. of
students:(𝒇)
Mid-value (𝐱) 𝒅 = 𝒙−𝟒𝟓
𝟏𝟎
𝒇𝒅 𝑓 𝒅 𝟐
10-20
20-30
30-40
40-50
50-60
60-70
70-80
5
12
15
20
10
4
2
Total 𝑓=N=68
-3
-2
-1
0
1
2
3
-15
-24
-15
0
10
8
6
𝑓𝑑=-30
45
48
15
0
10
16
18
𝑓 𝒅 𝟐
=152
Standard deviation=𝜎
= 𝑖 ×
𝑓𝑑2
𝑛
− 𝑓𝑑
𝑛
2
= 10 ×
152
68
− −30
68
2
= 4 − (−0.12)
15
25
35
45
55
65
75

20. It is possible to compute combined mean of two or more than two groups.
Combined Standard Deviation is denoted by 𝝈 𝟏𝟐
𝝈 𝟏𝟐=
𝑛1 𝜎1
2+𝑛2 𝜎2
2+𝑛1 𝑑1
2
+𝑛2 𝑑2
2
𝑛1+𝑛2
Where𝜎12 =combined standard deviation ,
𝜎1 = 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑓𝑖𝑟𝑠𝑡 𝑔𝑟𝑜𝑢𝑝𝜎2
= 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑠𝑒𝑐𝑜𝑛𝑑 𝑔𝑟𝑜𝑢𝑝𝑑1 = 𝑥1 − 𝑥12
𝑑2 = 𝑥2 − 𝑥12

21. a) Combined S.D. 𝝈 𝟏𝟐=
𝑛1 𝜎1
2+𝑛2 𝜎2
2+𝑛1 𝑑1
2
+𝑛2 𝑑2
2
𝑛1+𝑛2
combined Mean 𝑥12=
𝑛1 𝑥1+𝑛2 𝑥2
𝑛1+𝑛2
=
100 60 +50 45
100+50
=
6000+2250
150
= 55
𝑛1 = 100, 𝜎1
2 = 9, 𝑛2 = 50, 𝜎2
2 = 4,
𝑑1 = 𝑥1 − 𝑥12 = 60 − 55 = 5
𝑑2 = 𝑥2 − 𝑥12 = 45 − 55 = 10
The following are some of the particulars of the
distribution of weight of boys and girls in a class:
a) Find the standard deviation of the combined data
b) which of the two distributions is more variable
Boys Girls
Numbers 100 50
Mean weight 60 kg 45 kg
Variance(𝜎2
) 9 4
𝝈 𝟏𝟐=
100(9)+50(4)+100 5 2+50 10 2
100+50
=
900+200+2500+5000
150
= =
8600
150
= 7.57
b)
C.V (Boys)=
𝜎
𝑥1
× 100 =
3
60
× 100 = 5.00
C.V (Girls)=
𝜎
𝑥2
× 100 =
2
45
× 100 = 4.44

22. MERITS OF STANDARD DEVIATION
Very popular scientific measure of dispersion
From SD we can calculate Skewness, Correlation etc
It considers all the items of the series
The squaring of deviations make them positive and the
difficulty about algebraic signs which was expressed in case of
mean deviation is not found here.
22

23. DEMERITS OF STANDARD DEVIATION
• Calculation is difficult not as easier as Range and QD
• It always depends on AM
• Extreme items gain great importance
The formula of SD is =
𝑑2
𝑛
Problem: Calculate Standard Deviation of the following series
X – 40, 44, 54, 60, 62, 64, 70, 80, 90, 96
23

24. USES OF STANDARD DEVIATION
 It is widely used in biological studies .
 It is used in fitting a normal curve to a frequency distribution.
 It is most widely used measure of dispersion.
24