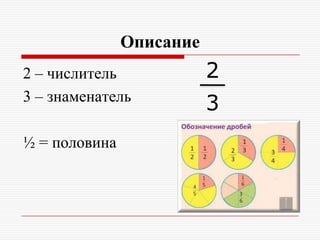
Документ содержит описание дробей, включая их виды (правильные, неправильные, смешанные) и правила работы с ними. Рассматриваются исторические аспекты дробей, такие как происхождение термина и первые описания десятичных дробей. Также в документе представлены правила сложения, вычитания, сравнения и сокращения дробей.

1. Дроби
Выполнила: ученица 5 «А»
класса МАОУ СОШ №132 г.
Екатеринбурга
Балахнина Алѐна

2. Описание
2 – числитель
3 – знаменатель
½ = половина
2
3

3. Из истории дробей
•«Дробь» - от глагола «дробить» (IIX
век).
•В первых учебниках математики их
называли «ломаными числами».
•Десятичные дроби используются чаще
обыкновенных из-за простоты
вычислений.
•Правила вычислений с десятичными
дробями описал ученый Средневековья
Аль- Каши.
•Десятичные дроби он записывал так же,
как принято сейчас, но не пользовался
запятой. Дробную часть писал красными
чернилами или отделял вертикальной
чертой.
•В России впервые написал о десятичных
дробях Л.Ф. Магницкий в 1703 г. в
первом учебнике математики.

4. Правильная дробь
Это дробь, у которой числитель
МЕНЬШЕ знаменателя
Примеры: ½ , 6/9 …

5. Неправильная дробь
Это дробь, у которой числитель
БОЛЬШЕ знаменателя.
Примеры:5/4, 7/3…

6. Смешанная дробь
Это дробь с выделенной целой
частью в составе числа
Примеры:7 1/8…
Смешанную дробь можно получить
из неправильной дроби.
Примеры: 3/2=3:2=1 1/2

7. Основное свойство дроби
Если числитель и знаменатель дроби
умножить или разделить на одно и то
же отличное от нуля число, то
получится дробь, равная данной.
Пример: 2/3=4/6=6/9= 8/12=10/15=… (в
первом случае мы умножили и числитель и знаменатель на 2)

8. Сложение и вычитание дробей
Правило 1: если знаменатели одинаковы, то мы
вычитаем/складываем числители, а знаменатель
оставляем неизменным.
Правило 2: если знаменатели не одинаковы, то
мы приводи к одному знаменателю дальше по 1
правилу. По возможности сократить.
Пример: п.1.:3/10+2/10=5/10=1/2
п.2.:2/3 + 4/5 = 2*5/3 + 4*3/5 = 10/15 + 12/15 =
=22/15

9. Сравнение дробей
1. Из двух дробей с одинаковыми
числителями больше та, у которой знаменатель
меньше.
2. Из двух дробей с одинаковыми знаменате-
лями больше та, у которой числитель больше.
3. Если и числители и знаменатели разные,
то надо привести к общему знаменателю и
сравнить их по вышеизложенному правилу.

10. Сокращение дробей
4/6 =2/3 – сократили на 2
5/25 =1/5 – сократили на 5
32/24 =4/3 – сократили на 8

11. Всем спасибо за внимание!