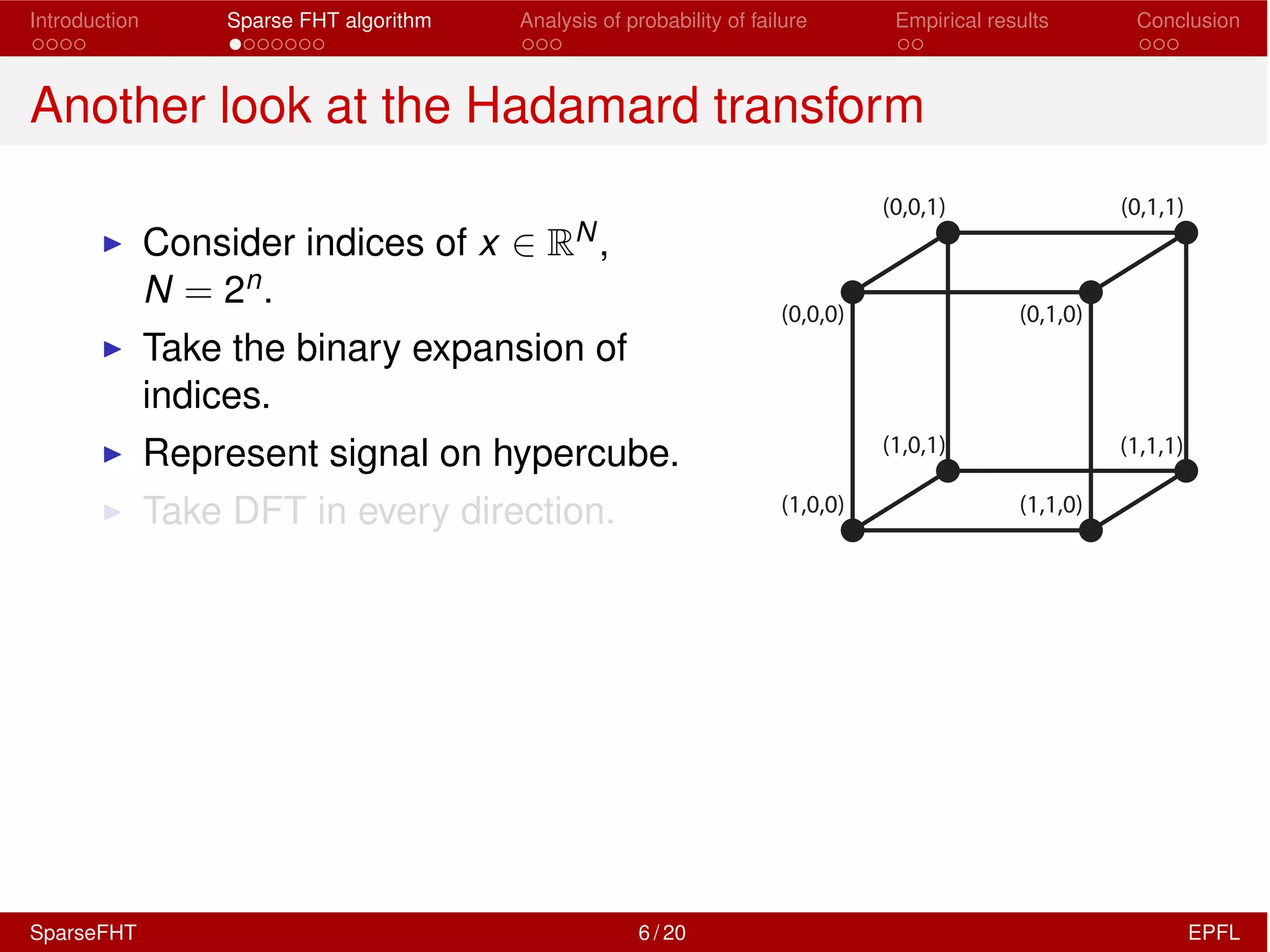
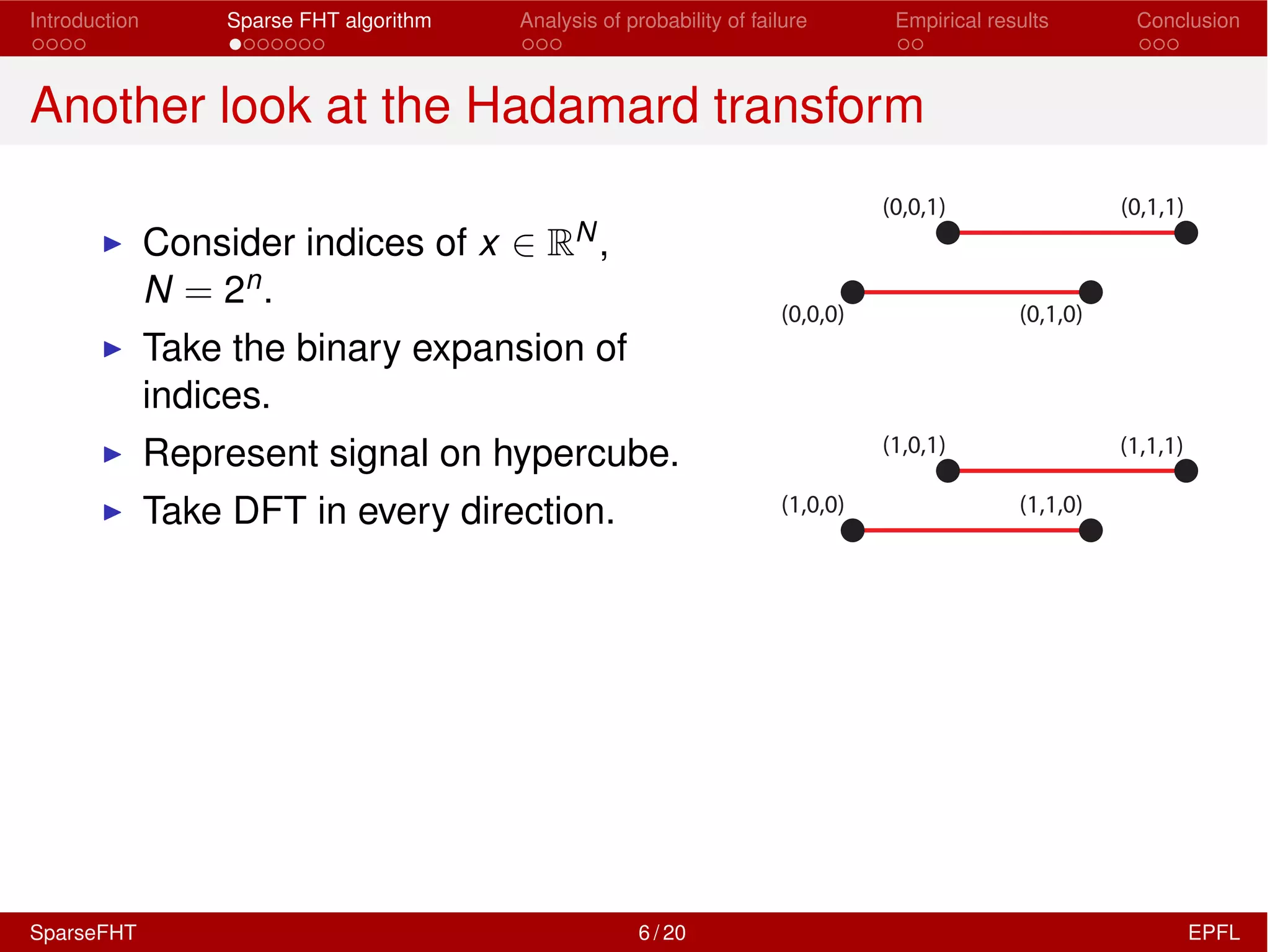
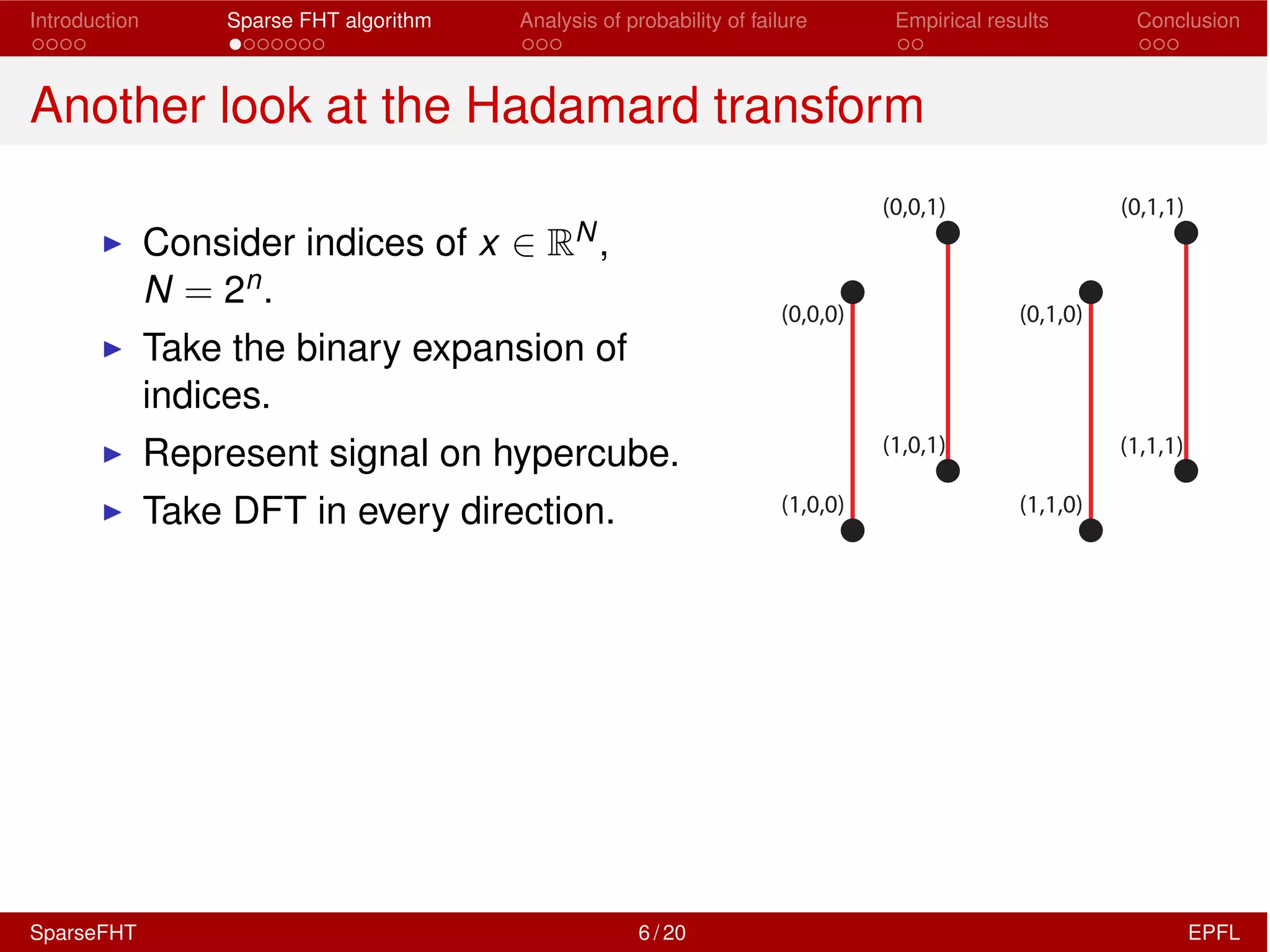
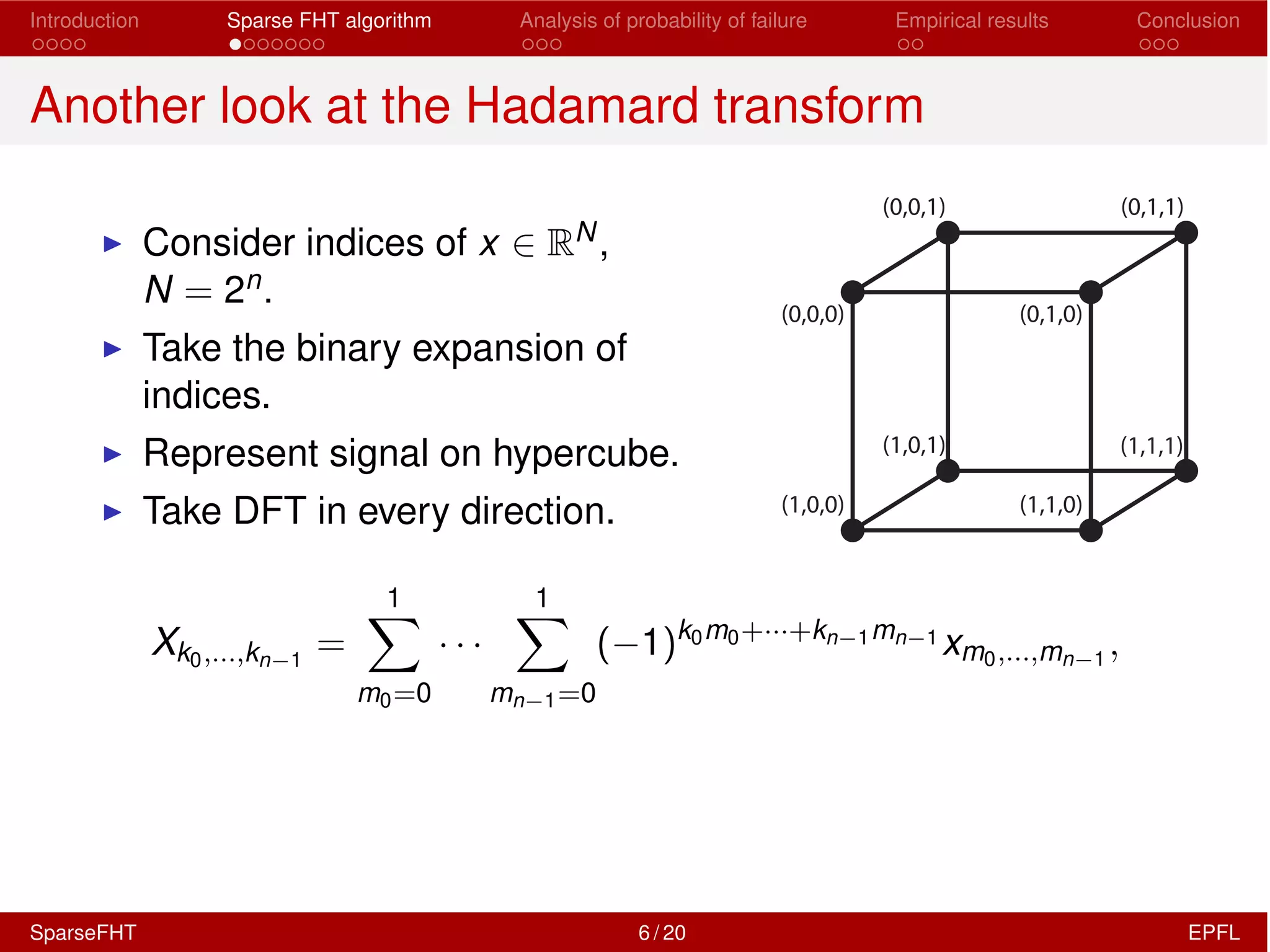
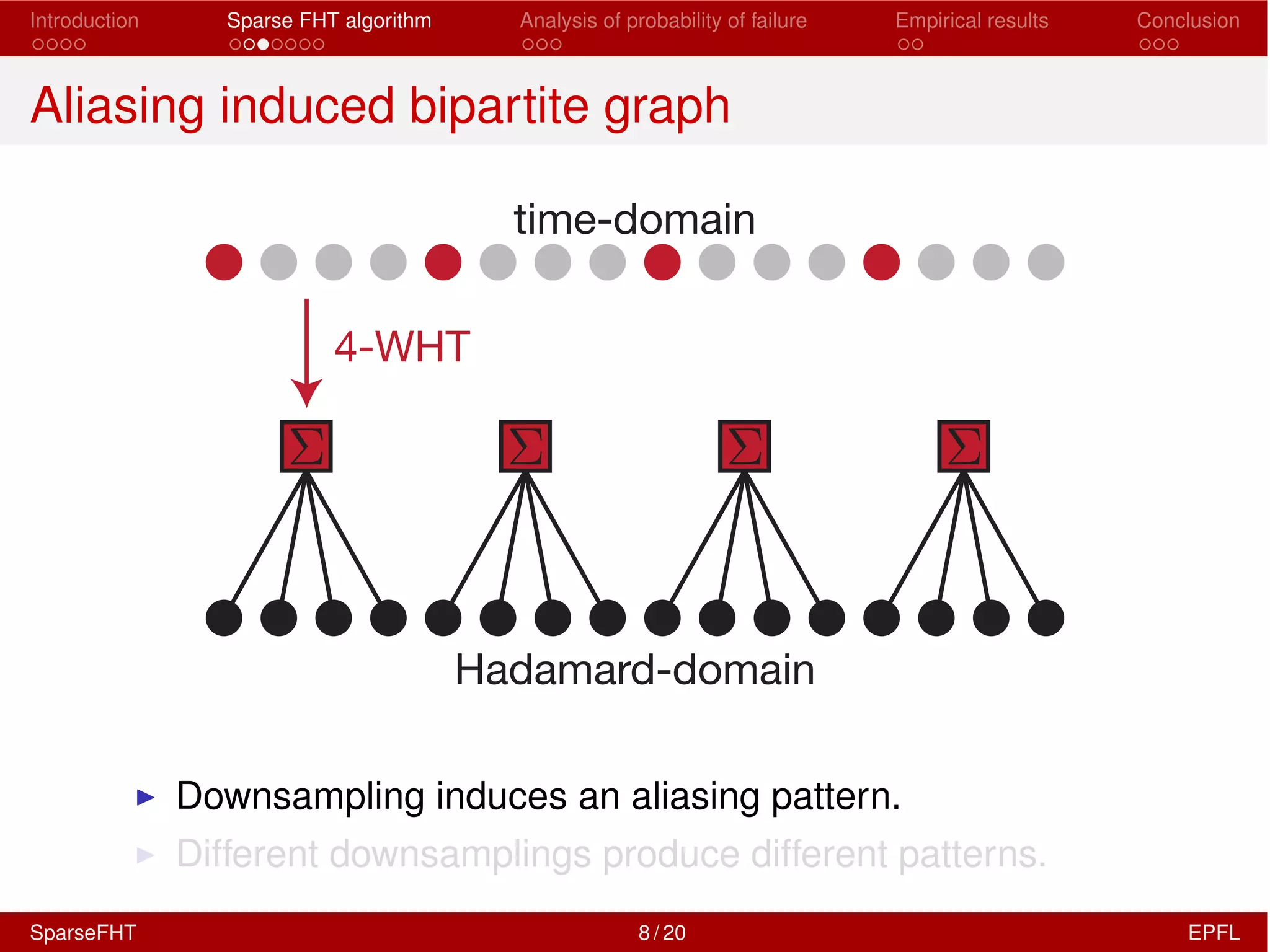
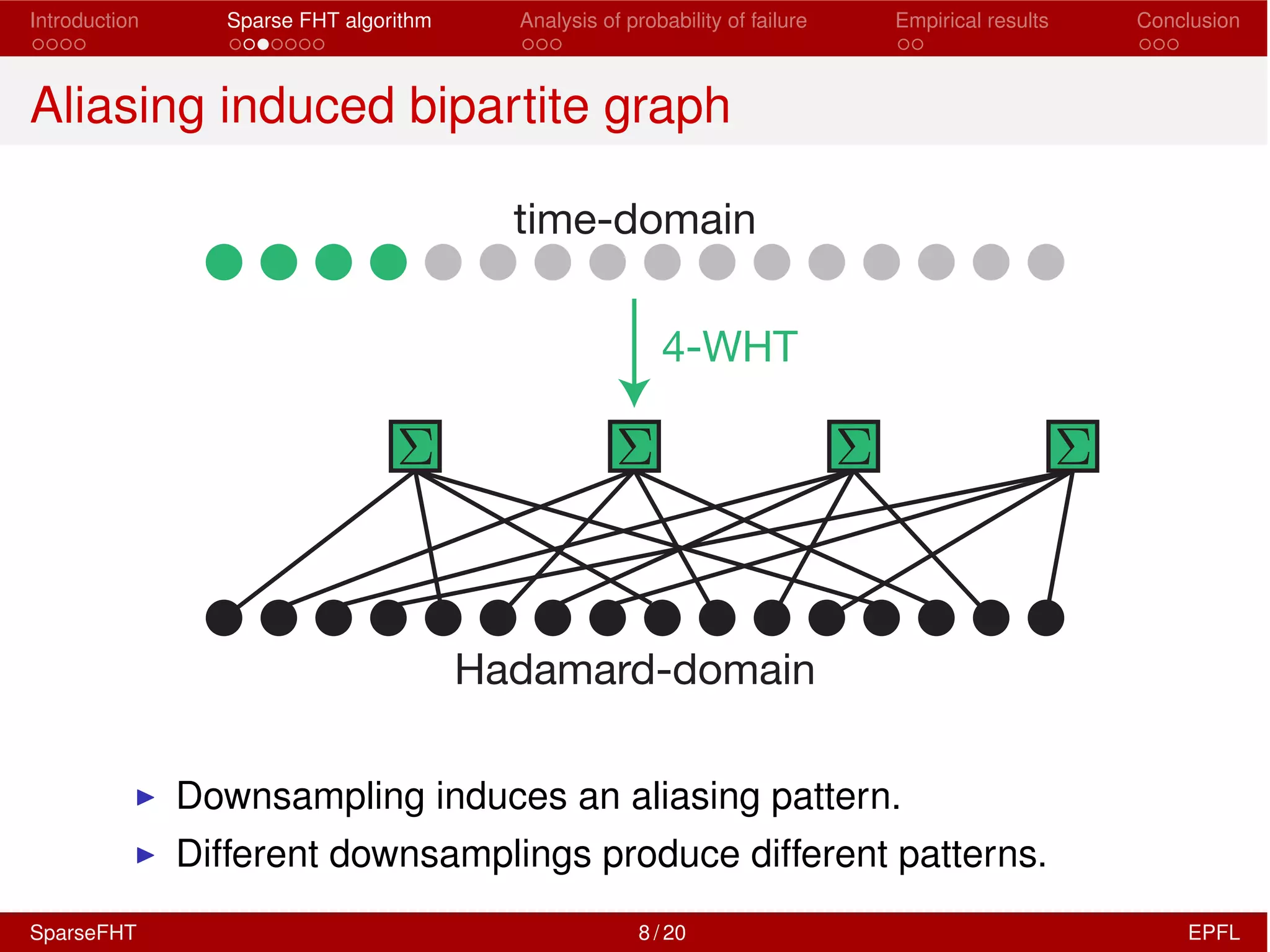
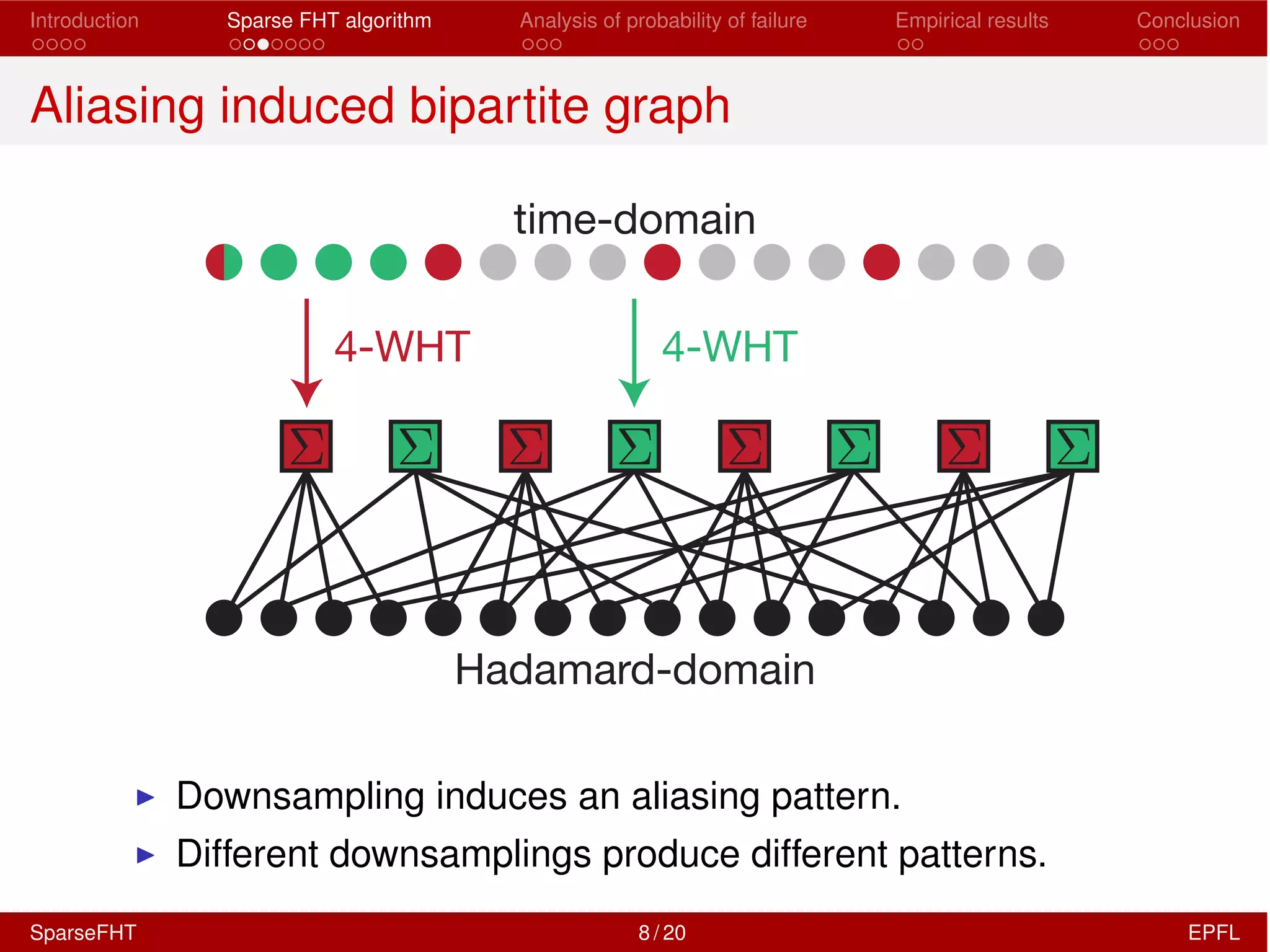
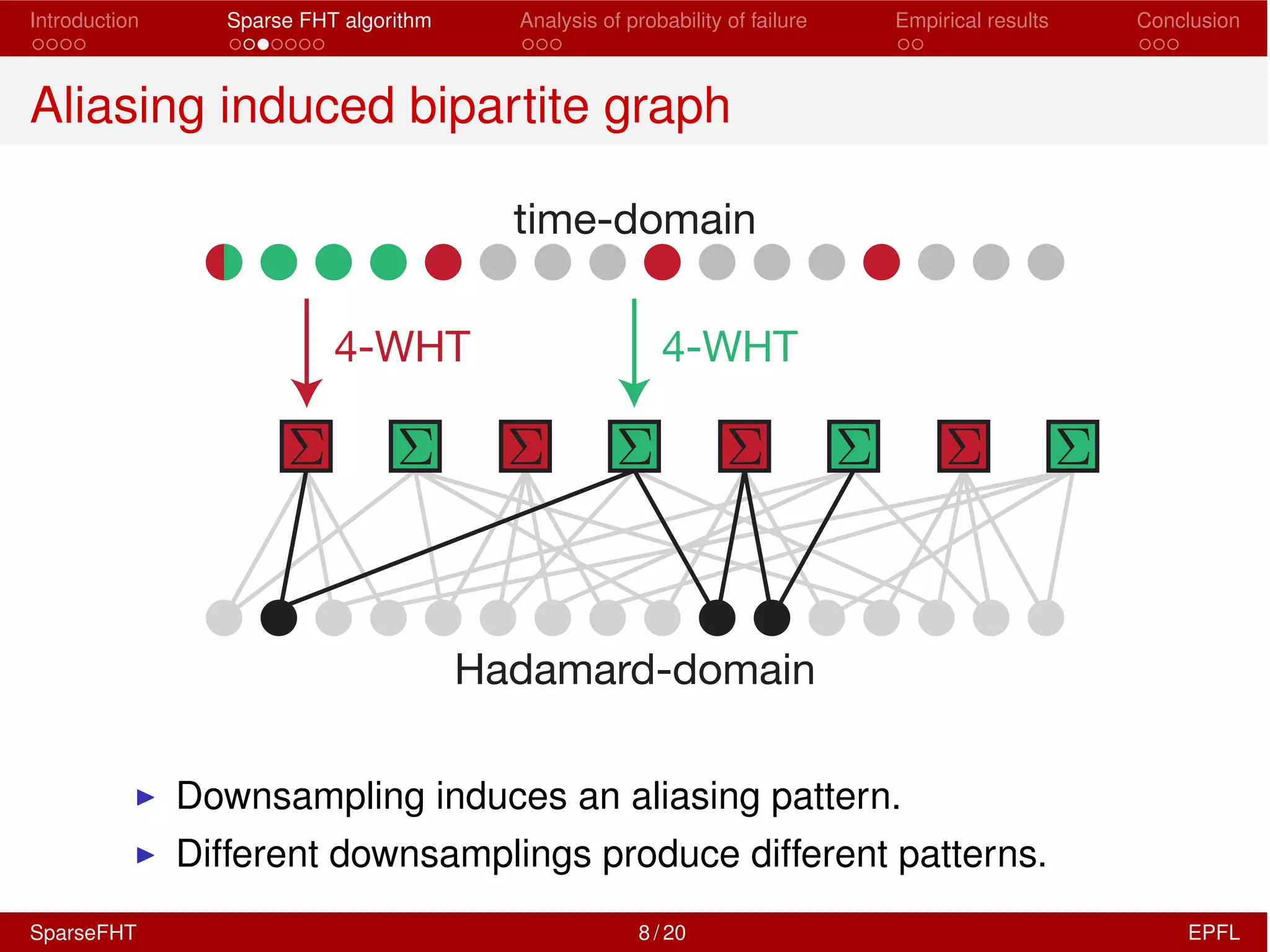
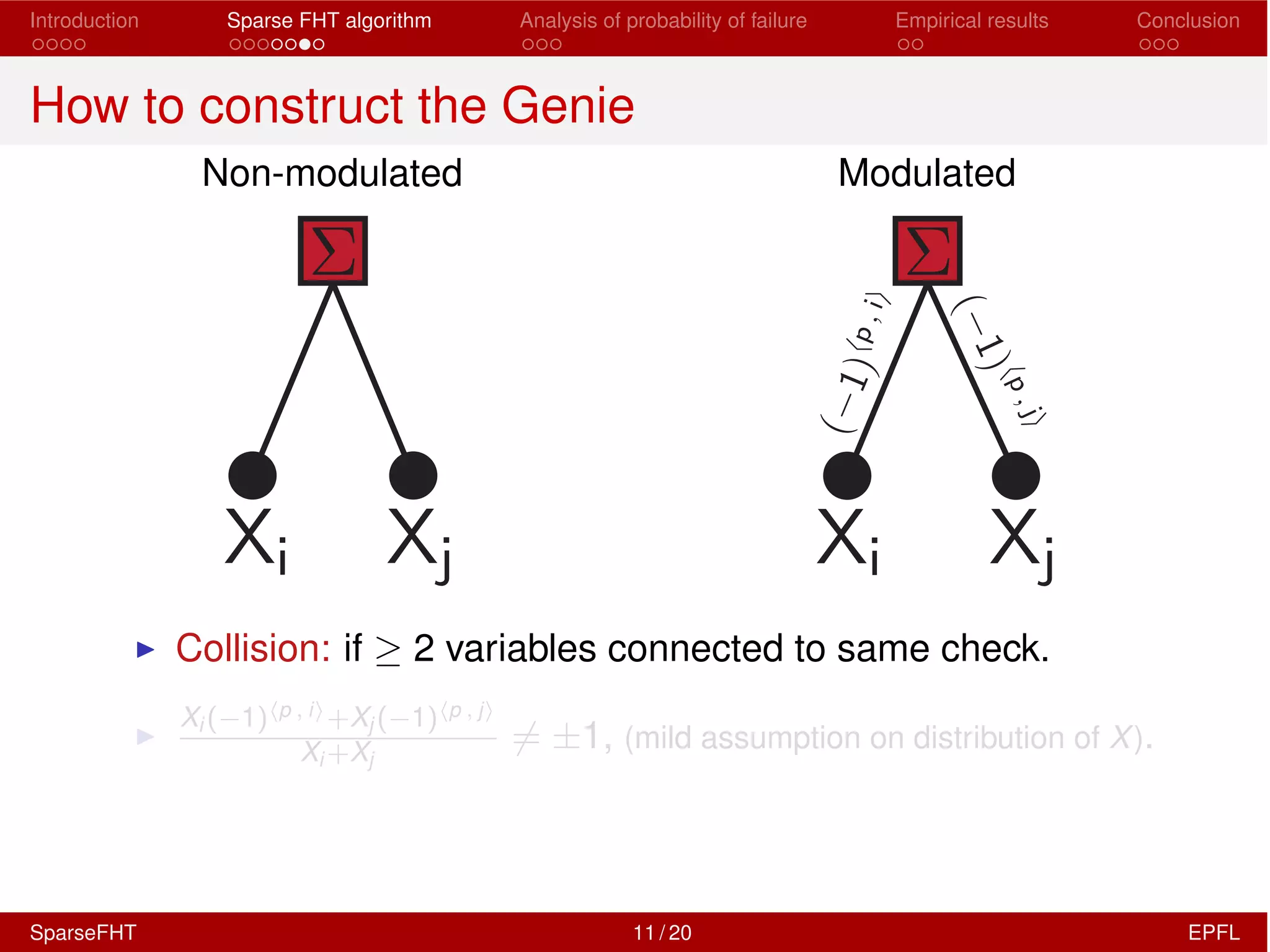
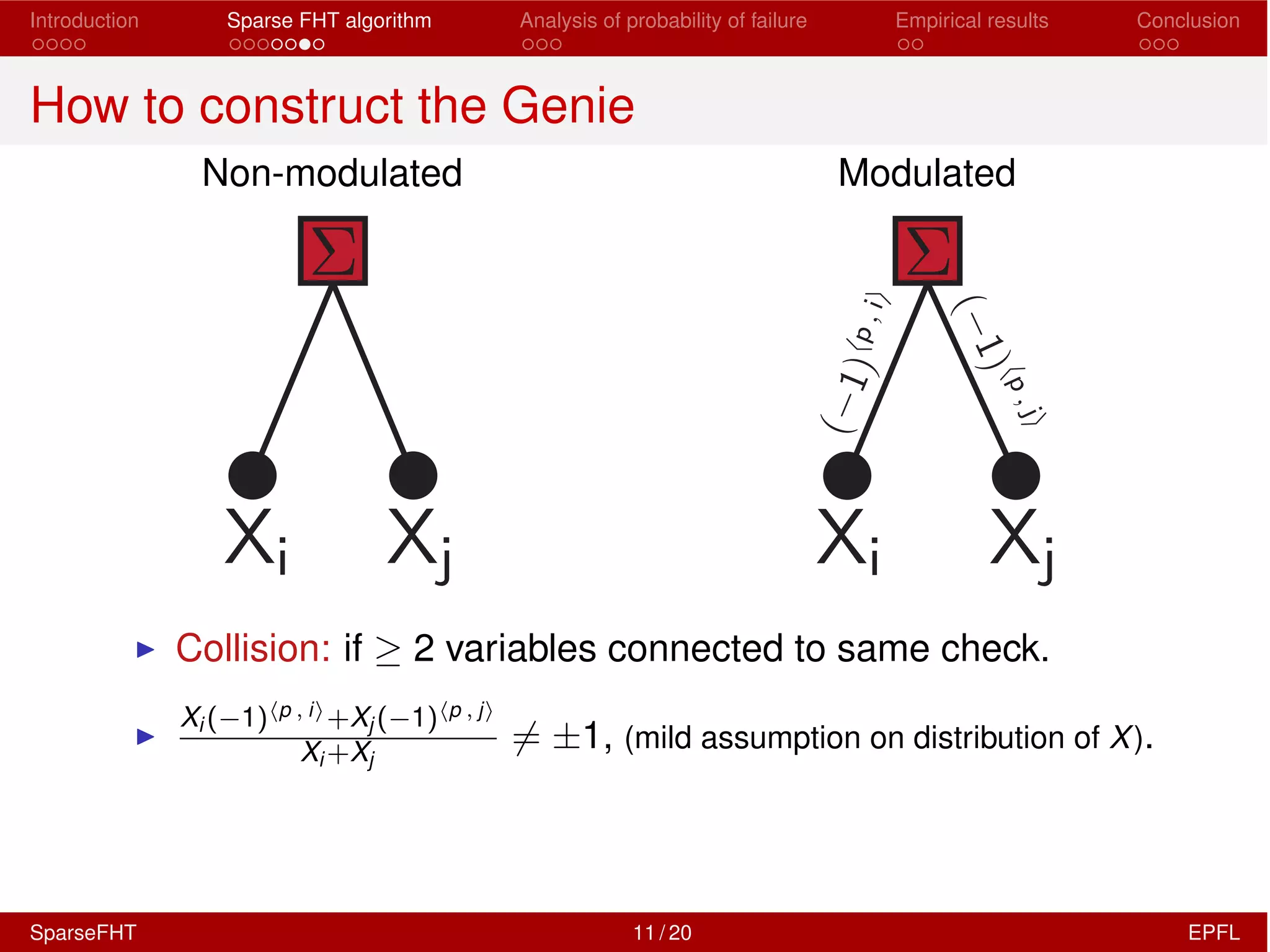
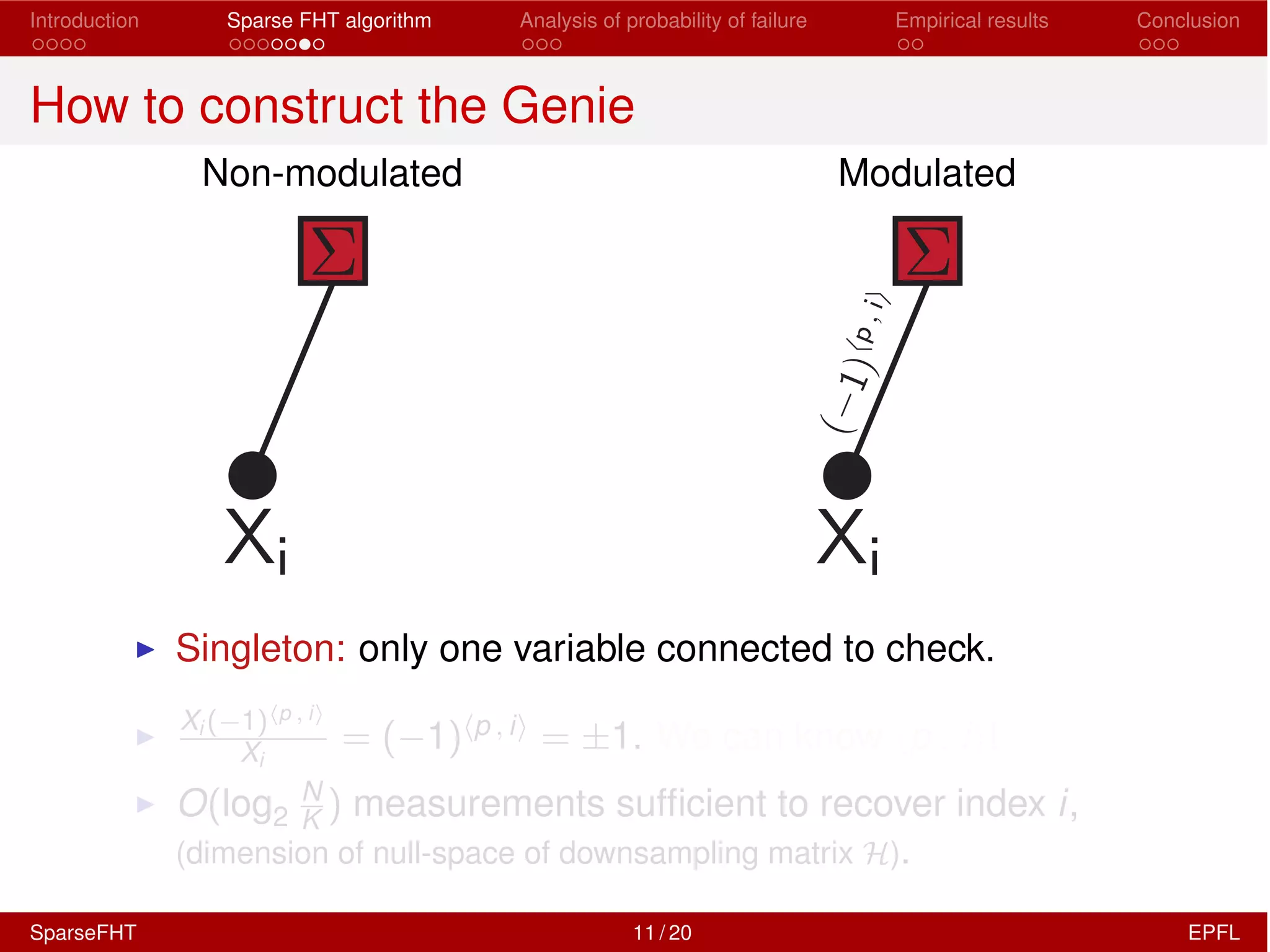
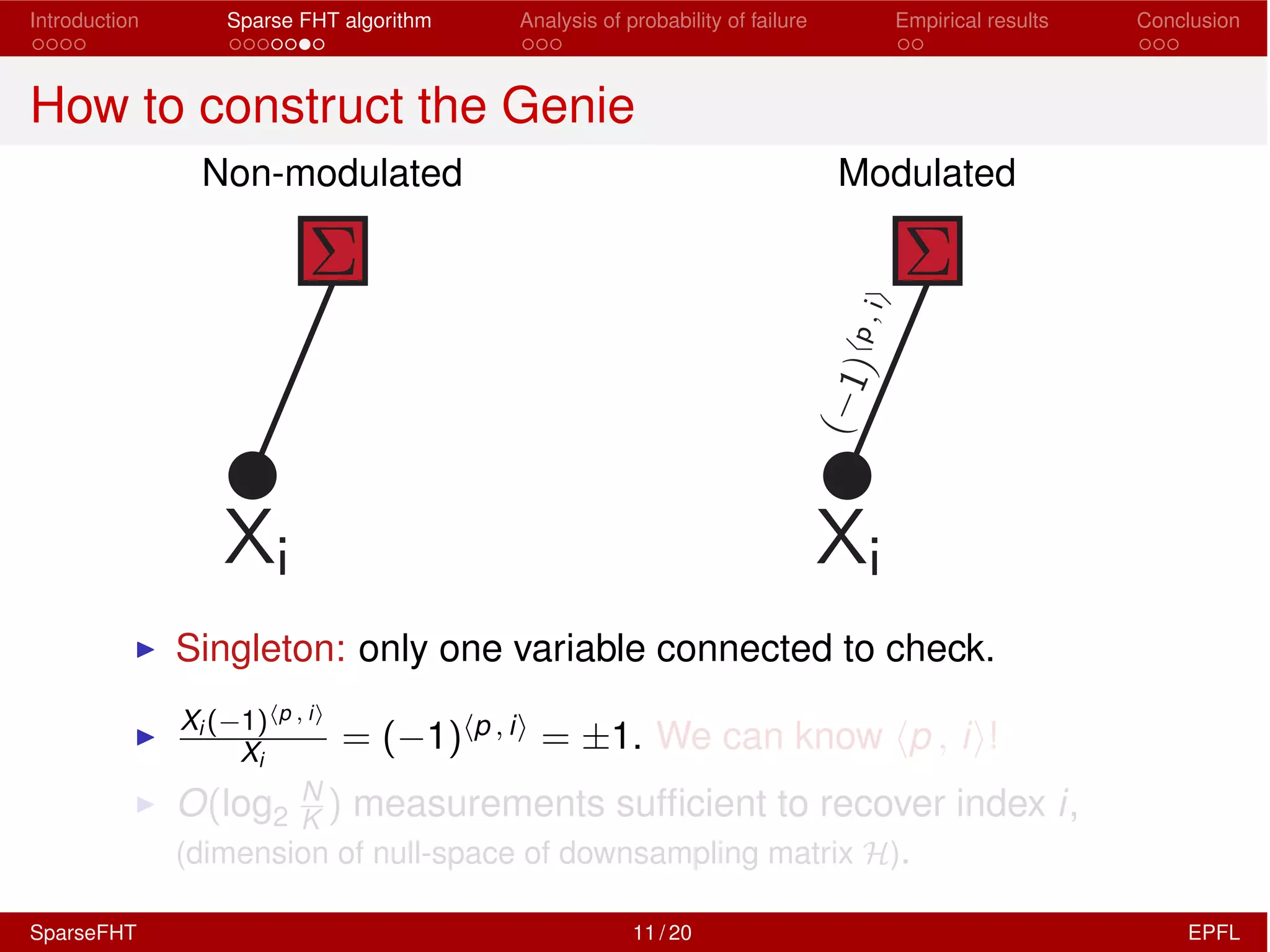
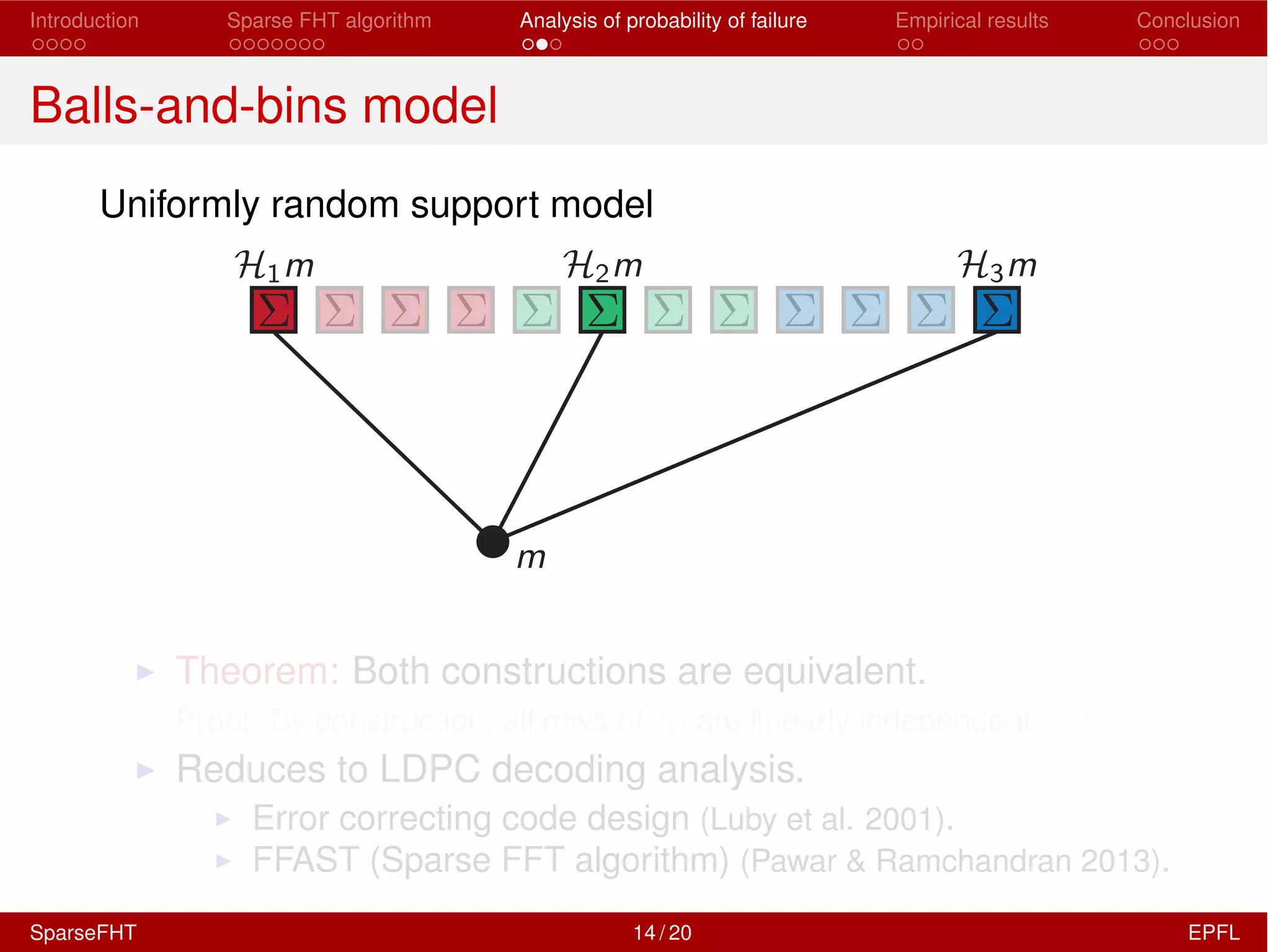
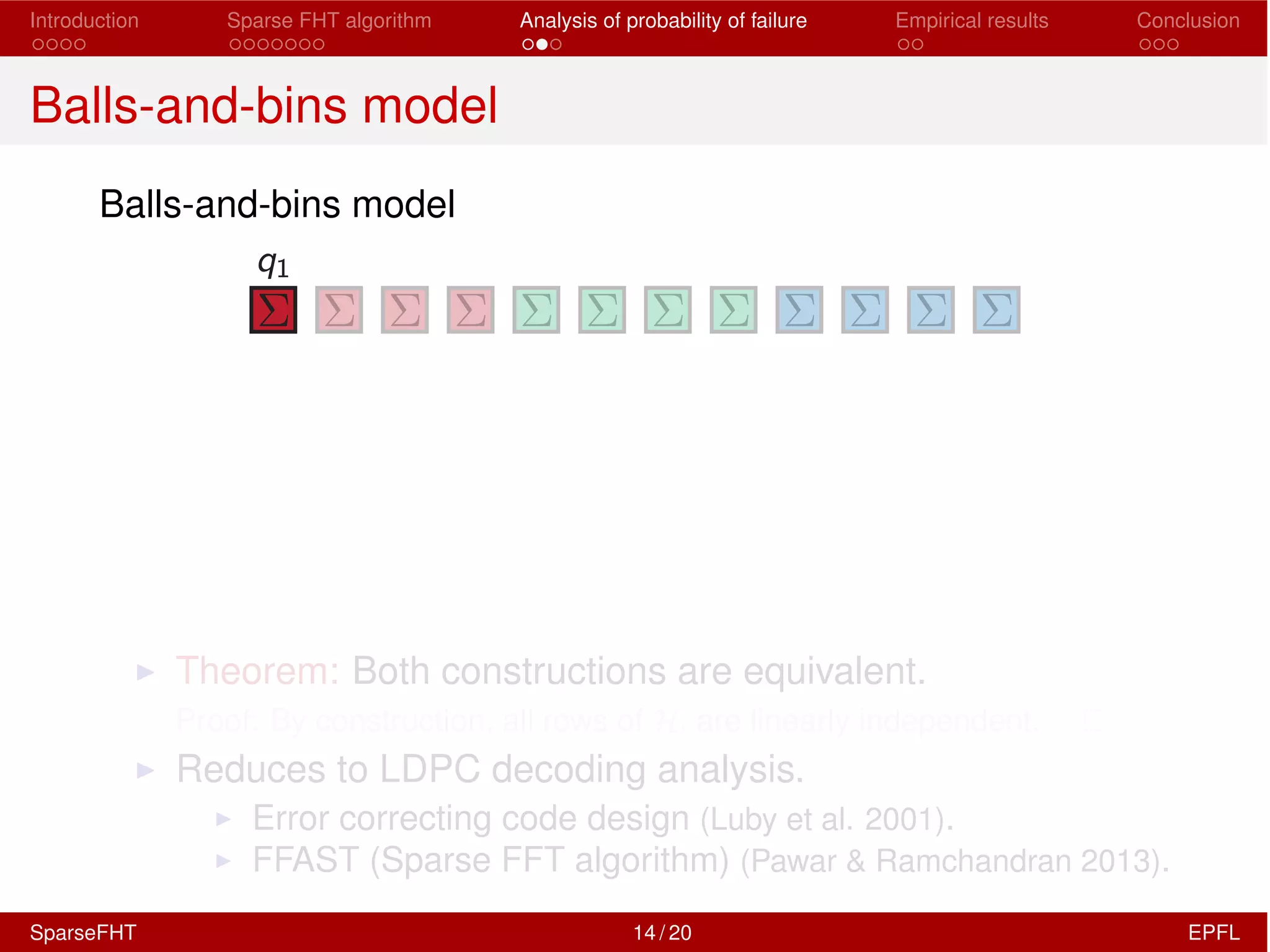
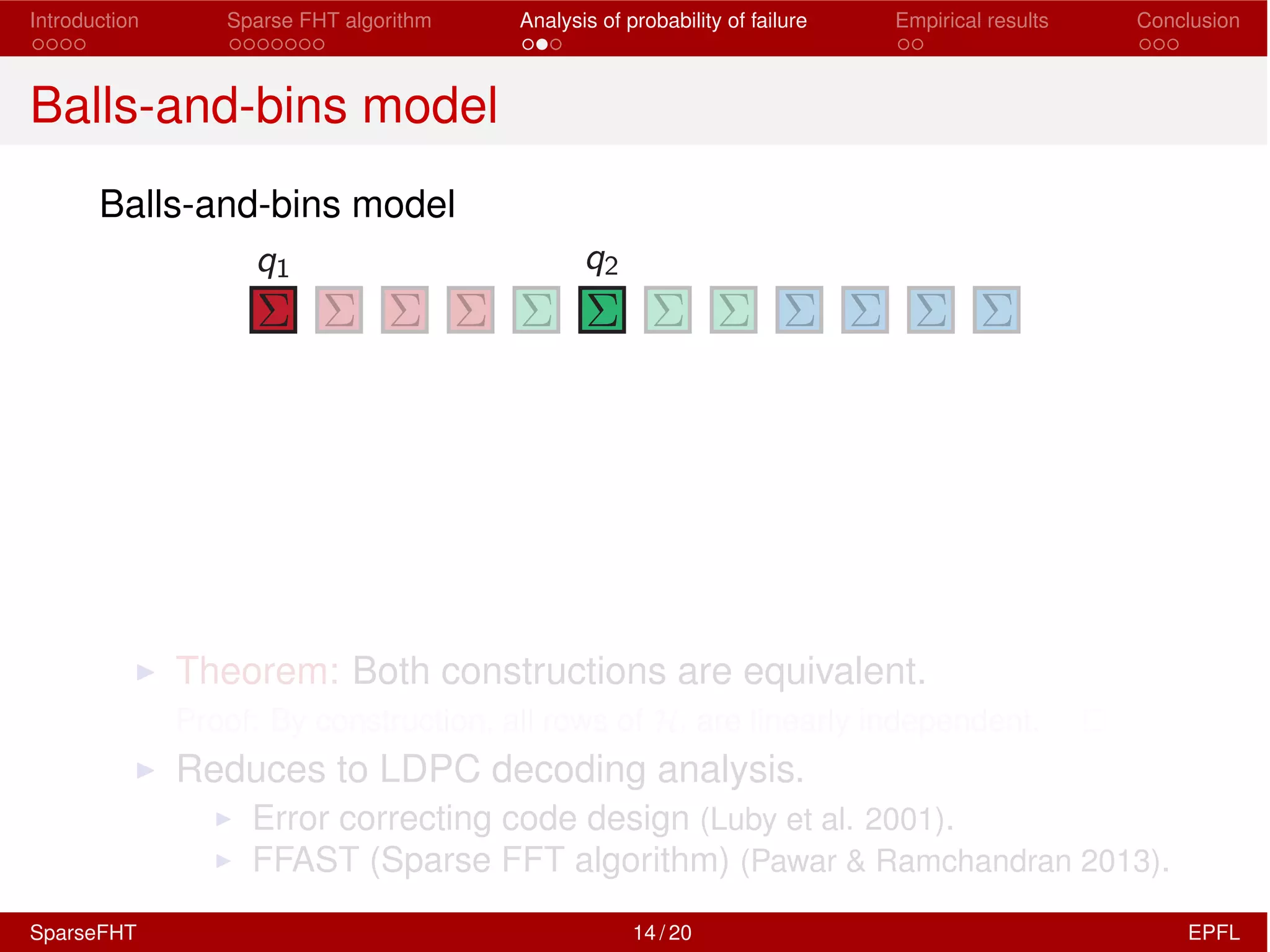
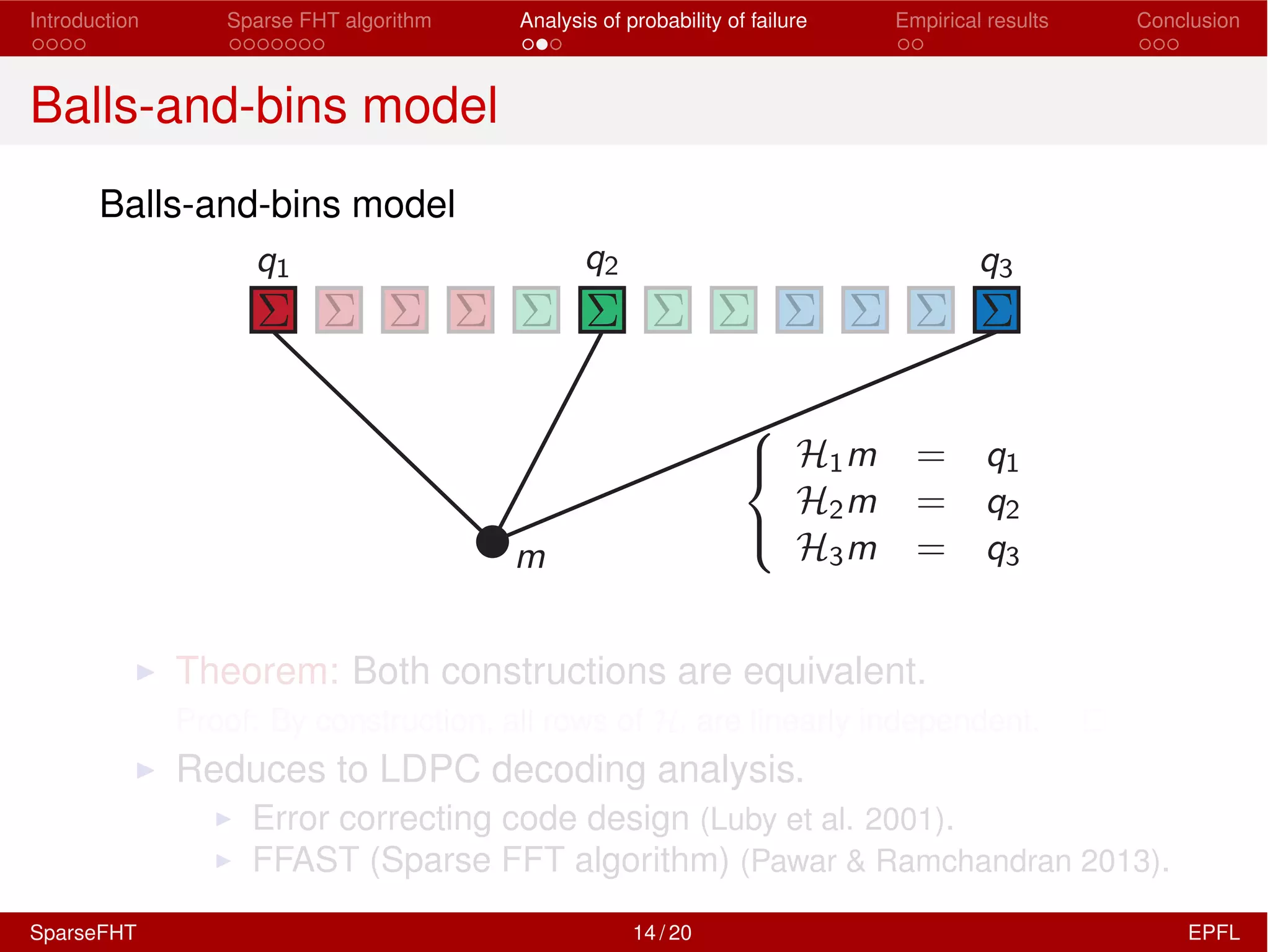
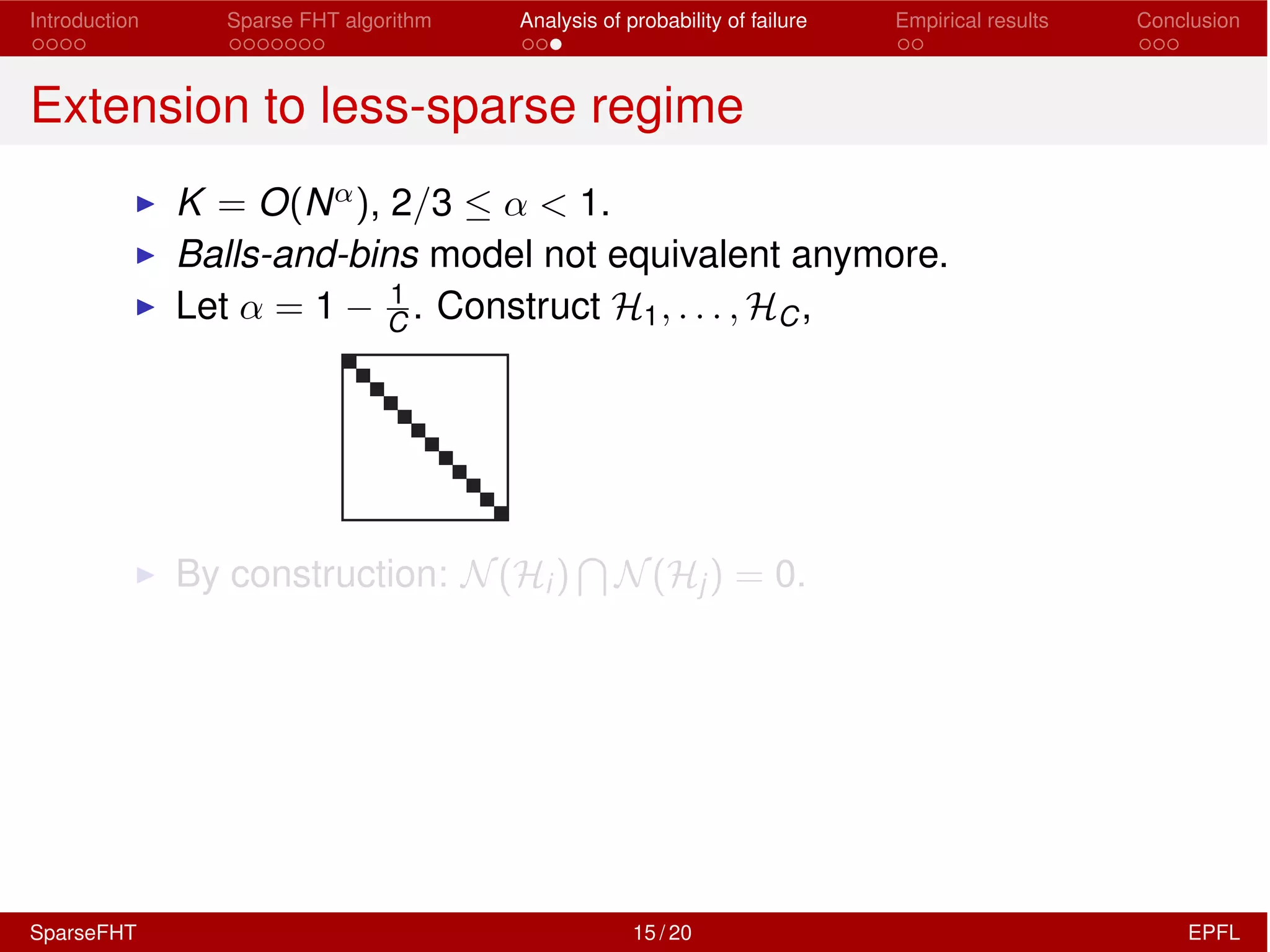
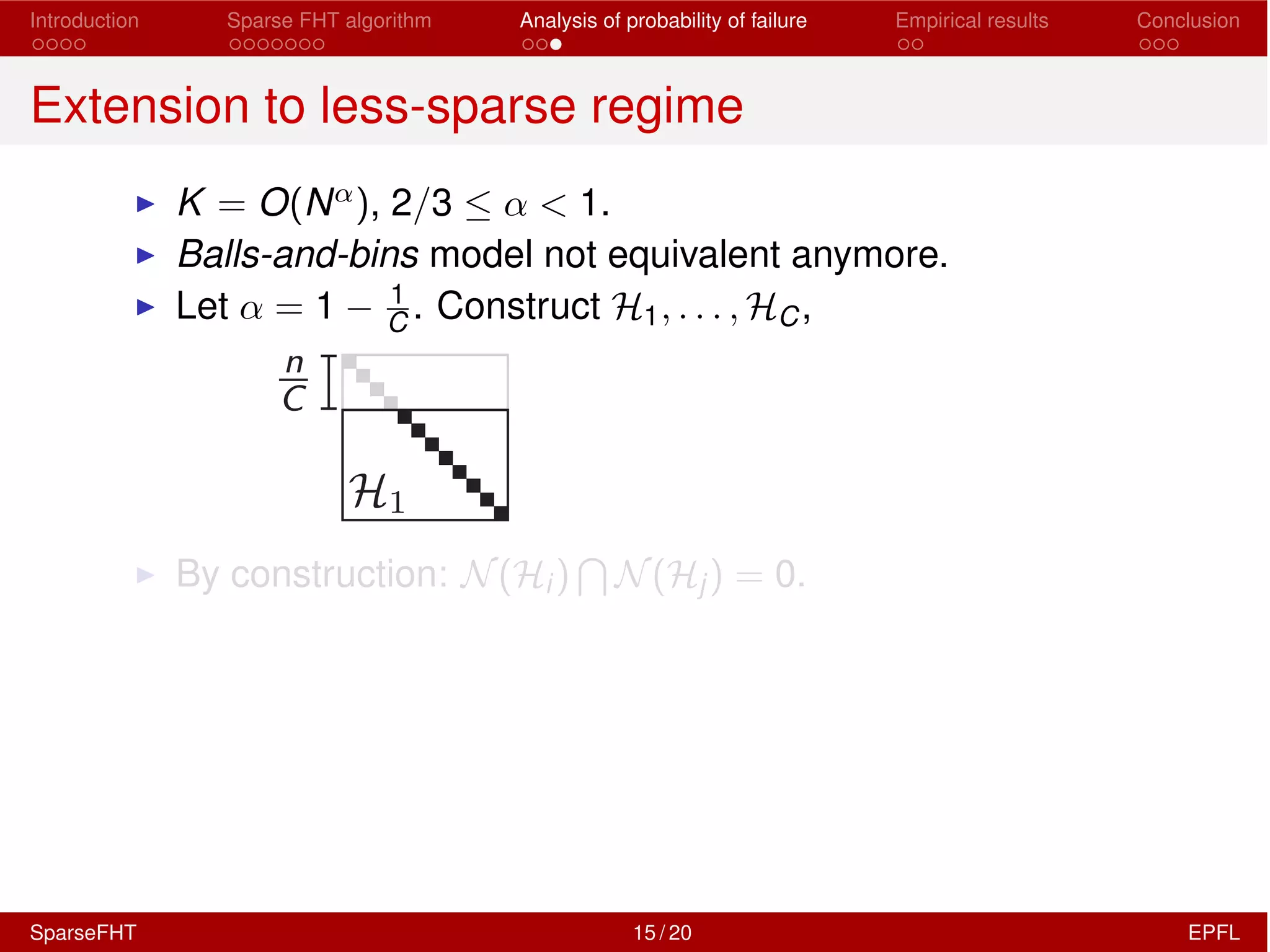
The document discusses the development of a Sparse Fast Hadamard Transform (Sparse FHT) algorithm which efficiently computes the non-zero coefficients of k-sparse signals in a universal setting. It highlights the algorithm's improvements over traditional Hadamard transforms, achieving faster computation times and reduced sample complexity. Empirical results and analyses of failure probabilities reinforce the efficacy of this new algorithm.

1. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
A Fast Hadamard Transform for Signals with
Sub-linear Sparsity
Robin Scheibler Saeid Haghighatshoar Martin Vetterli
School of Computer and Communication Sciences
École Polytechnique Fédérale de Lausanne, Switzerland
October 28, 2013
SparseFHT 1 / 20 EPFL

2. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Why the Hadamard transform ?
I Historically, low computation
approximation to DFT.
I Coding, 1969 Mariner Mars probe.
I Communication, orthogonal codes
in WCDMA.
I Compressed sensing, maximally
incoherent with Dirac basis.
I Spectroscopy, design of
instruments with lower noise.
I Recent advances in sparse FFT.
16 ⇥ 16 Hadamard matrix
Mariner probe
SparseFHT 2 / 20 EPFL

3. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Fast Hadamard transform
I Butterfly structure similar to FFT.
I Time complexity O(N log2 N).
I Sample complexity N.
+ Universal, i.e. works for all signals.
Does not exploit signal structure
(e.g. sparsity).
Can we do better ?
SparseFHT 3 / 20 EPFL

4. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Fast Hadamard transform
I Butterfly structure similar to FFT.
I Time complexity O(N log2 N).
I Sample complexity N.
+ Universal, i.e. works for all signals.
Does not exploit signal structure
(e.g. sparsity).
Can we do better ?
SparseFHT 3 / 20 EPFL

5. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Fast Hadamard transform
I Butterfly structure similar to FFT.
I Time complexity O(N log2 N).
I Sample complexity N.
+ Universal, i.e. works for all signals.
Does not exploit signal structure
(e.g. sparsity).
Can we do better ?
SparseFHT 3 / 20 EPFL

6. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Fast Hadamard transform
I Butterfly structure similar to FFT.
I Time complexity O(N log2 N).
I Sample complexity N.
+ Universal, i.e. works for all signals.
Does not exploit signal structure
(e.g. sparsity).
Can we do better ?
SparseFHT 3 / 20 EPFL

7. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Contribution: Sparse fast Hadamard transform
Assumptions
I The signal is exaclty K-sparse in the transform domain.
I Sub-linear sparsity regime K = O(N↵), 0 < ↵ < 1.
I Support of the signal is uniformly random.
Contribution
An algorithm computing the K non-zero coefficients with:
I Time complexity O(K log2 K log2
N
K ).
I Sample complexity O(K log2
N
K ).
I Probability of failure asymptotically vanishes.
SparseFHT 4 / 20 EPFL

8. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Contribution: Sparse fast Hadamard transform
Assumptions
I The signal is exaclty K-sparse in the transform domain.
I Sub-linear sparsity regime K = O(N↵), 0 < ↵ < 1.
I Support of the signal is uniformly random.
Contribution
An algorithm computing the K non-zero coefficients with:
I Time complexity O(K log2 K log2
N
K ).
I Sample complexity O(K log2
N
K ).
I Probability of failure asymptotically vanishes.
SparseFHT 4 / 20 EPFL

9. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Outline
1. Sparse FHT algorithm
2. Analysis of probability of failure
3. Empirical results
SparseFHT 5 / 20 EPFL

10. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
I = {0, . . . , 23
1}
SparseFHT 6 / 20 EPFL

11. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
I = {(0, 0, 0), . . . , (1, 1, 1)}
SparseFHT 6 / 20 EPFL

12. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
SparseFHT 6 / 20 EPFL

13. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
SparseFHT 6 / 20 EPFL

14. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
SparseFHT 6 / 20 EPFL

15. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
SparseFHT 6 / 20 EPFL

16. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
Xk0,...,kn 1
=
1X
m0=0
· · ·
1X
mn 1=0
( 1)k0m0+···+kn 1mn 1
xm0,...,mn 1
,
SparseFHT 6 / 20 EPFL

17. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
Xk =
X
m2Fn
2
( 1)hk , mi
xm, k, m 2 Fn
2, hk , mi =
n 1X
i=0
ki mi.
Treat indices as binary vectors.
SparseFHT 6 / 20 EPFL

18. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Another look at the Hadamard transform
I Consider indices of x 2 RN,
N = 2n.
I Take the binary expansion of
indices.
I Represent signal on hypercube.
I Take DFT in every direction.
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(1,1,0)(1,0,0)
(0,0,1) (0,1,1)
Xk =
X
m2Fn
2
( 1)hk , mi
xm, k, m 2 Fn
2, hk , mi =
n 1X
i=0
ki mi.
Treat indices as binary vectors.
SparseFHT 6 / 20 EPFL

19. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Hadamard property I: downsampling/aliasing
Given B = 2b, a divider of N = 2n, and H 2 Fb⇥n
2 ,
where rows of H are a subset of rows of identity matrix,
xHT m
WHT
!
X
i2N(H)
XHT k+i, m, k 2 Fb
2.
e.g. H =
⇥
0b⇥(n b) Ib
⇤
selects the b high order bits.
SparseFHT 7 / 20 EPFL

20. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Hadamard property I: downsampling/aliasing
Given B = 2b, a divider of N = 2n, and H 2 Fb⇥n
2 ,
where rows of H are a subset of rows of identity matrix,
xHT m
WHT
!
X
i2N(H)
XHT k+i, m, k 2 Fb
2.
e.g. H =
⇥
0b⇥(n b) Ib
⇤
selects the b high order bits.
SparseFHT 7 / 20 EPFL

21. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Hadamard property I: downsampling/aliasing
Given B = 2b, a divider of N = 2n, and H 2 Fb⇥n
2 ,
where rows of H are a subset of rows of identity matrix,
xHT m
WHT
!
X
i2N(H)
XHT k+i, m, k 2 Fb
2.
e.g. H =
⇥
0b⇥(n b) Ib
⇤
selects the b high order bits.
(0,0,0) (0,1,0)
(1,0,1)
(1,1,1)(0,1,1)(0,0,1)
(1,0,0) (1,1,0)
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(0,1,1)
(0,0,1)
(1,0,0) (1,1,0)
WHT
SparseFHT 7 / 20 EPFL

22. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Hadamard property I: downsampling/aliasing
Given B = 2b, a divider of N = 2n, and H 2 Fb⇥n
2 ,
where rows of H are a subset of rows of identity matrix,
xHT m
WHT
!
X
i2N(H)
XHT k+i, m, k 2 Fb
2.
e.g. H =
⇥
0b⇥(n b) Ib
⇤
selects the b high order bits.
(0,0,0) (0,1,0)
(0,1,1)(0,0,1)
(0,0,0) (0,1,0)
(1,0,1) (1,1,1)
(0,1,1)
(0,0,1)
(1,0,0) (1,1,0)
(1,0,1)
(1,1,1)
(1,0,0) (1,1,0)
WHT
SparseFHT 7 / 20 EPFL

23. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Aliasing induced bipartite graph
time-domain
Hadamard-domain
I Downsampling induces an aliasing pattern.
I Different downsamplings produce different patterns.
SparseFHT 8 / 20 EPFL

24. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Aliasing induced bipartite graph
time-domain
Hadamard-domain
4-WHT
I Downsampling induces an aliasing pattern.
I Different downsamplings produce different patterns.
SparseFHT 8 / 20 EPFL

25. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Aliasing induced bipartite graph
time-domain
Hadamard-domain
4-WHT
I Downsampling induces an aliasing pattern.
I Different downsamplings produce different patterns.
SparseFHT 8 / 20 EPFL

26. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Aliasing induced bipartite graph
time-domain
Hadamard-domain
4-WHT 4-WHT
I Downsampling induces an aliasing pattern.
I Different downsamplings produce different patterns.
SparseFHT 8 / 20 EPFL

27. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Aliasing induced bipartite graph
time-domain
Hadamard-domain
4-WHT 4-WHT
I Downsampling induces an aliasing pattern.
I Different downsamplings produce different patterns.
SparseFHT 8 / 20 EPFL

28. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Aliasing induced bipartite graph
time-domain
Hadamard-domain
4-WHT 4-WHT
Checks
Variables
I Downsampling induces an aliasing pattern.
I Different downsamplings produce different patterns.
SparseFHT 8 / 20 EPFL

29. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

30. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

31. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

32. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

33. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

34. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

35. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Genie-aided peeling decoder
A genie indicates us
I if a check is connected to only one variable (singleton),
I in that case, the genie also gives the index of that variable.
Success
Peeling decoder algorithm:
1. Find a singleton check: {X1, X8, X11}
2. Peel it off.
3. Repeat until nothing left.
SparseFHT 9 / 20 EPFL

36. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Hadamard property II: shift/modulation
Theorem (shift/modulation)
Given p 2 Fn
2,
xm+p
WHT
! Xk ( 1)hp , ki
.
Consequence
The signal can be modulated in frequency by manipulating the
time-domain samples.
SparseFHT 10 / 20 EPFL

37. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Hadamard property II: shift/modulation
Theorem (shift/modulation)
Given p 2 Fn
2,
xm+p
WHT
! Xk ( 1)hp , ki
.
Consequence
The signal can be modulated in frequency by manipulating the
time-domain samples.
SparseFHT 10 / 20 EPFL

38. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Collision: if 2 variables connected to same check.
I
Xi ( 1)hp , ii+Xj ( 1)hp , ji
Xi +Xj
6= ±1, (mild assumption on distribution of X).
SparseFHT 11 / 20 EPFL

39. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Collision: if 2 variables connected to same check.
I
Xi ( 1)hp , ii+Xj ( 1)hp , ji
Xi +Xj
6= ±1, (mild assumption on distribution of X).
SparseFHT 11 / 20 EPFL

40. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Collision: if 2 variables connected to same check.
I
Xi ( 1)hp , ii+Xj ( 1)hp , ji
Xi +Xj
6= ±1, (mild assumption on distribution of X).
SparseFHT 11 / 20 EPFL

41. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Singleton: only one variable connected to check.
I
Xi ( 1)hp , ii
Xi
= ( 1)hp , ii = ±1. We can know hp , ii!
I O(log2
N
K ) measurements sufficient to recover index i,
(dimension of null-space of downsampling matrix H).
SparseFHT 11 / 20 EPFL

42. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Singleton: only one variable connected to check.
I
Xi ( 1)hp , ii
Xi
= ( 1)hp , ii = ±1. We can know hp , ii!
I O(log2
N
K ) measurements sufficient to recover index i,
(dimension of null-space of downsampling matrix H).
SparseFHT 11 / 20 EPFL

43. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Singleton: only one variable connected to check.
I
Xi ( 1)hp , ii
Xi
= ( 1)hp , ii = ±1. We can know hp , ii!
I O(log2
N
K ) measurements sufficient to recover index i,
(dimension of null-space of downsampling matrix H).
SparseFHT 11 / 20 EPFL

44. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
How to construct the Genie
Non-modulated Modulated
I Singleton: only one variable connected to check.
I
Xi ( 1)hp , ii
Xi
= ( 1)hp , ii = ±1. We can know hp , ii!
I O(log2
N
K ) measurements sufficient to recover index i,
(dimension of null-space of downsampling matrix H).
SparseFHT 11 / 20 EPFL

45. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Sparse fast Hadamard transform
Algorithm
1. Set number of checks per downsampling B = O(K).
2. Choose C downsampling matrices H1, . . . , HC.
3. Compute C(log2 N/K + 1) size-K fast Hadamard
transform, each takes O(K log2 K).
4. Decode non-zero coefficients using peeling decoder.
Performance
I Time complexity – O(K log2 K log2 N/K).
I Sample complexity – O(K log2
N
K ).
I How to construct H1, . . . , HC ? Probability of success ?
SparseFHT 12 / 20 EPFL

46. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Sparse fast Hadamard transform
Algorithm
1. Set number of checks per downsampling B = O(K).
2. Choose C downsampling matrices H1, . . . , HC.
3. Compute C(log2 N/K + 1) size-K fast Hadamard
transform, each takes O(K log2 K).
4. Decode non-zero coefficients using peeling decoder.
Performance
I Time complexity – O(K log2 K log2 N/K).
I Sample complexity – O(K log2
N
K ).
I How to construct H1, . . . , HC ? Probability of success ?
SparseFHT 12 / 20 EPFL

47. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Sparse fast Hadamard transform
Algorithm
1. Set number of checks per downsampling B = O(K).
2. Choose C downsampling matrices H1, . . . , HC.
3. Compute C(log2 N/K + 1) size-K fast Hadamard
transform, each takes O(K log2 K).
4. Decode non-zero coefficients using peeling decoder.
Performance
I Time complexity – O(K log2 K log2 N/K).
I Sample complexity – O(K log2
N
K ).
I How to construct H1, . . . , HC ? Probability of success ?
SparseFHT 12 / 20 EPFL

48. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Very sparse regime
Setting
I K = O(N↵), 0 < ↵ < 1/3.
I Uniformly random support.
I Study asymptotic probability of failure as n ! 1.
Downsampling matrices construction
I Achieves values ↵ = 1
C , i.e. b = n
C .
I Deterministic downsampling matrices H1, . . . , HC,
SparseFHT 13 / 20 EPFL

49. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Very sparse regime
Setting
I K = O(N↵), 0 < ↵ < 1/3.
I Uniformly random support.
I Study asymptotic probability of failure as n ! 1.
Downsampling matrices construction
I Achieves values ↵ = 1
C , i.e. b = n
C .
I Deterministic downsampling matrices H1, . . . , HC,
SparseFHT 13 / 20 EPFL

50. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Very sparse regime
Setting
I K = O(N↵), 0 < ↵ < 1/3.
I Uniformly random support.
I Study asymptotic probability of failure as n ! 1.
Downsampling matrices construction
I Achieves values ↵ = 1
C , i.e. b = n
C .
I Deterministic downsampling matrices H1, . . . , HC,
SparseFHT 13 / 20 EPFL

51. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Very sparse regime
Setting
I K = O(N↵), 0 < ↵ < 1/3.
I Uniformly random support.
I Study asymptotic probability of failure as n ! 1.
Downsampling matrices construction
I Achieves values ↵ = 1
C , i.e. b = n
C .
I Deterministic downsampling matrices H1, . . . , HC,
SparseFHT 13 / 20 EPFL

52. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Very sparse regime
Setting
I K = O(N↵), 0 < ↵ < 1/3.
I Uniformly random support.
I Study asymptotic probability of failure as n ! 1.
Downsampling matrices construction
I Achieves values ↵ = 1
C , i.e. b = n
C .
I Deterministic downsampling matrices H1, . . . , HC,
SparseFHT 13 / 20 EPFL

53. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Very sparse regime
Setting
I K = O(N↵), 0 < ↵ < 1/3.
I Uniformly random support.
I Study asymptotic probability of failure as n ! 1.
Downsampling matrices construction
I Achieves values ↵ = 1
C , i.e. b = n
C .
I Deterministic downsampling matrices H1, . . . , HC,
SparseFHT 13 / 20 EPFL

54. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Uniformly random support model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

55. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Uniformly random support model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

56. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Uniformly random support model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

57. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Uniformly random support model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

58. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Uniformly random support model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

59. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

60. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

61. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

62. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

63. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

64. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

65. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

66. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

67. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Balls-and-bins model
Balls-and-bins model
I Theorem: Both constructions are equivalent.
Proof: By construction, all rows of Hi are linearly independent.
I Reduces to LDPC decoding analysis.
I Error correcting code design (Luby et al. 2001).
I FFAST (Sparse FFT algorithm) (Pawar & Ramchandran 2013).
SparseFHT 14 / 20 EPFL

68. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

69. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

70. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

71. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

72. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

73. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

74. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

75. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

76. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

77. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Extension to less-sparse regime
I K = O(N↵), 2/3  ↵ < 1.
I Balls-and-bins model not equivalent anymore.
I Let ↵ = 1 1
C . Construct H1, . . . , HC,
I By construction: N(Hi)
T
N(Hj) = 0.
SparseFHT 15 / 20 EPFL

78. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
SparseFHT – Probability of success
Probability of success - N = 222
0 1/3 2/3 1
0
0.2
0.4
0.6
0.8
1
↵
SparseFHT 16 / 20 EPFL

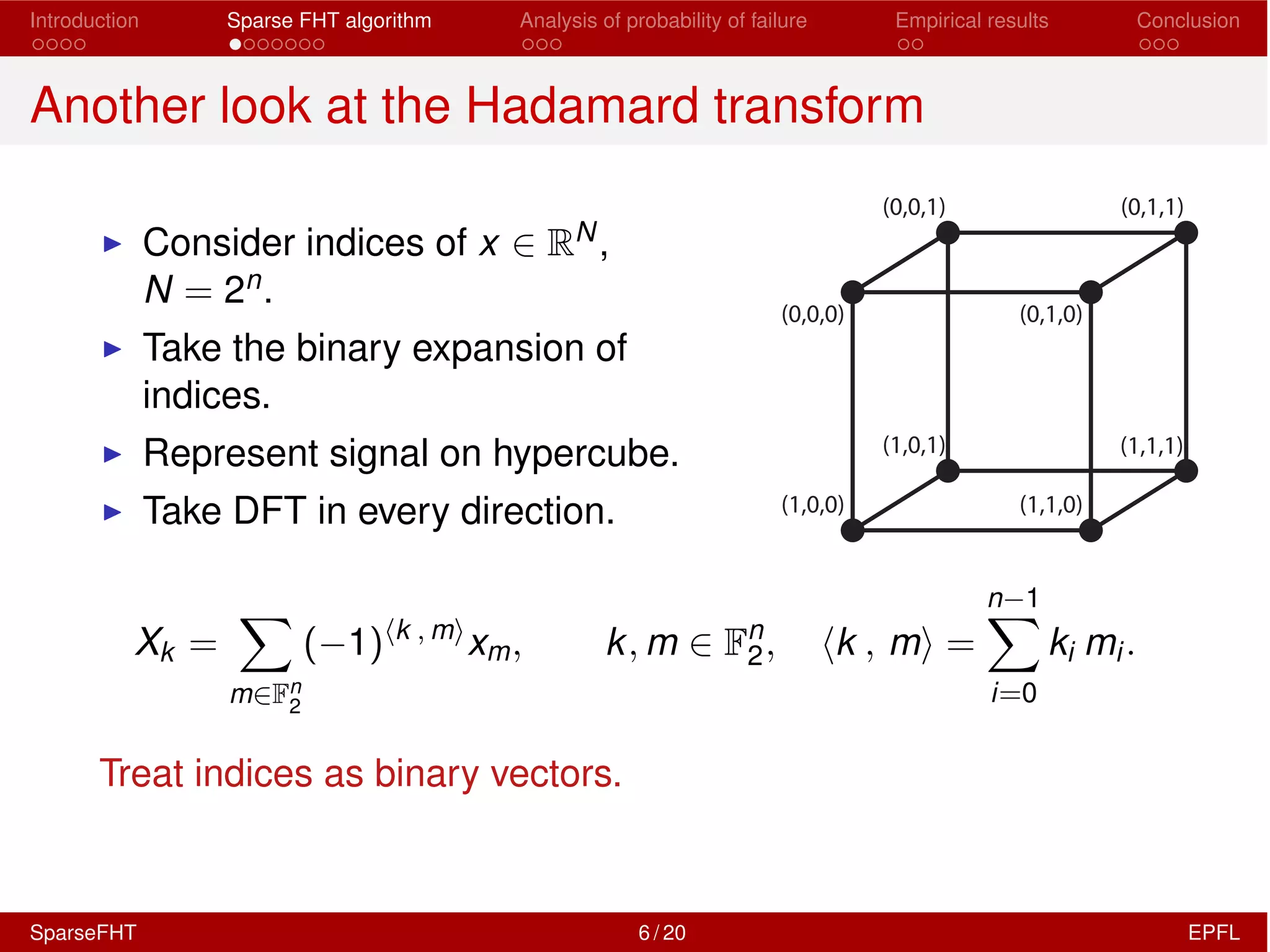
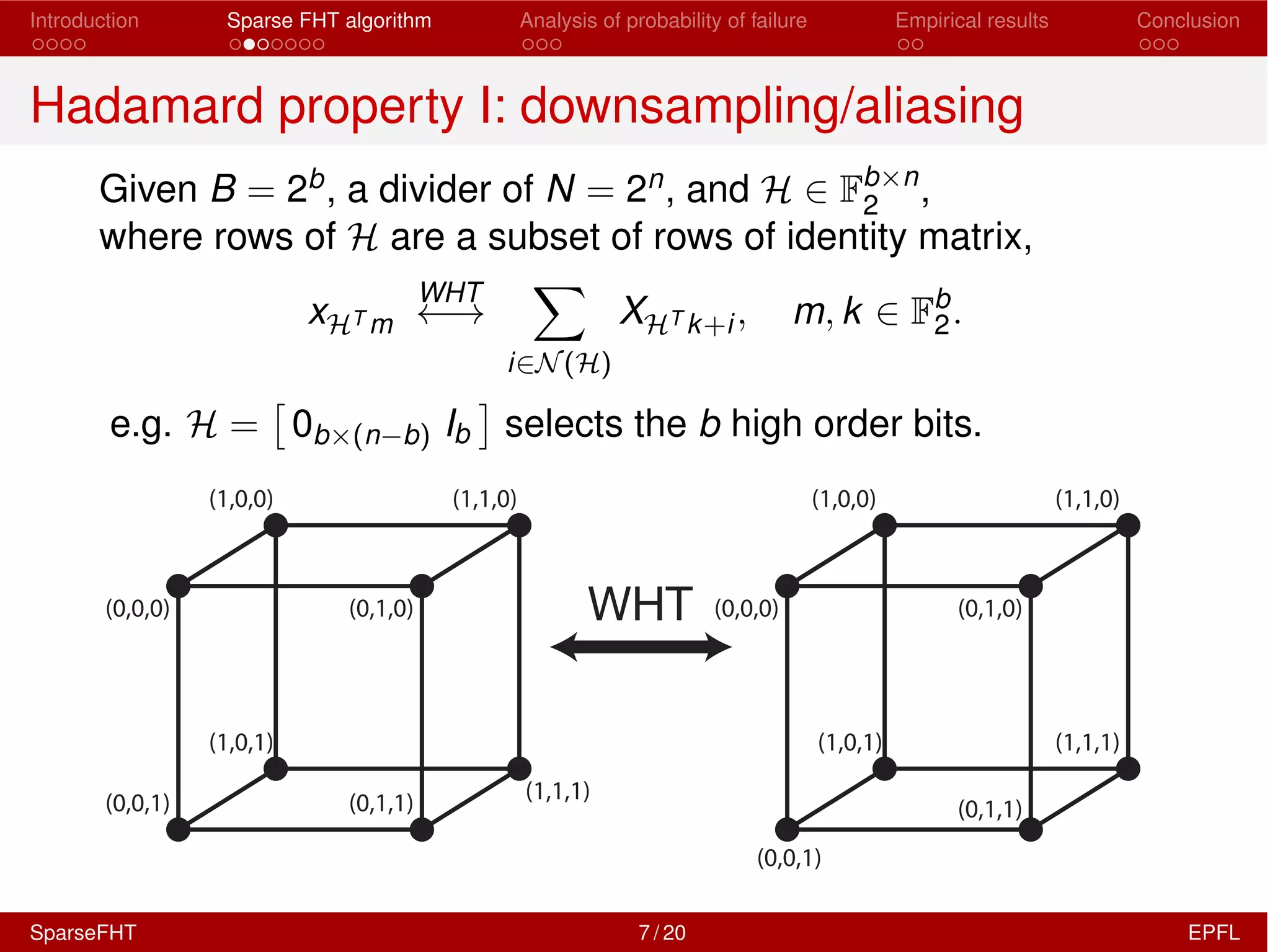
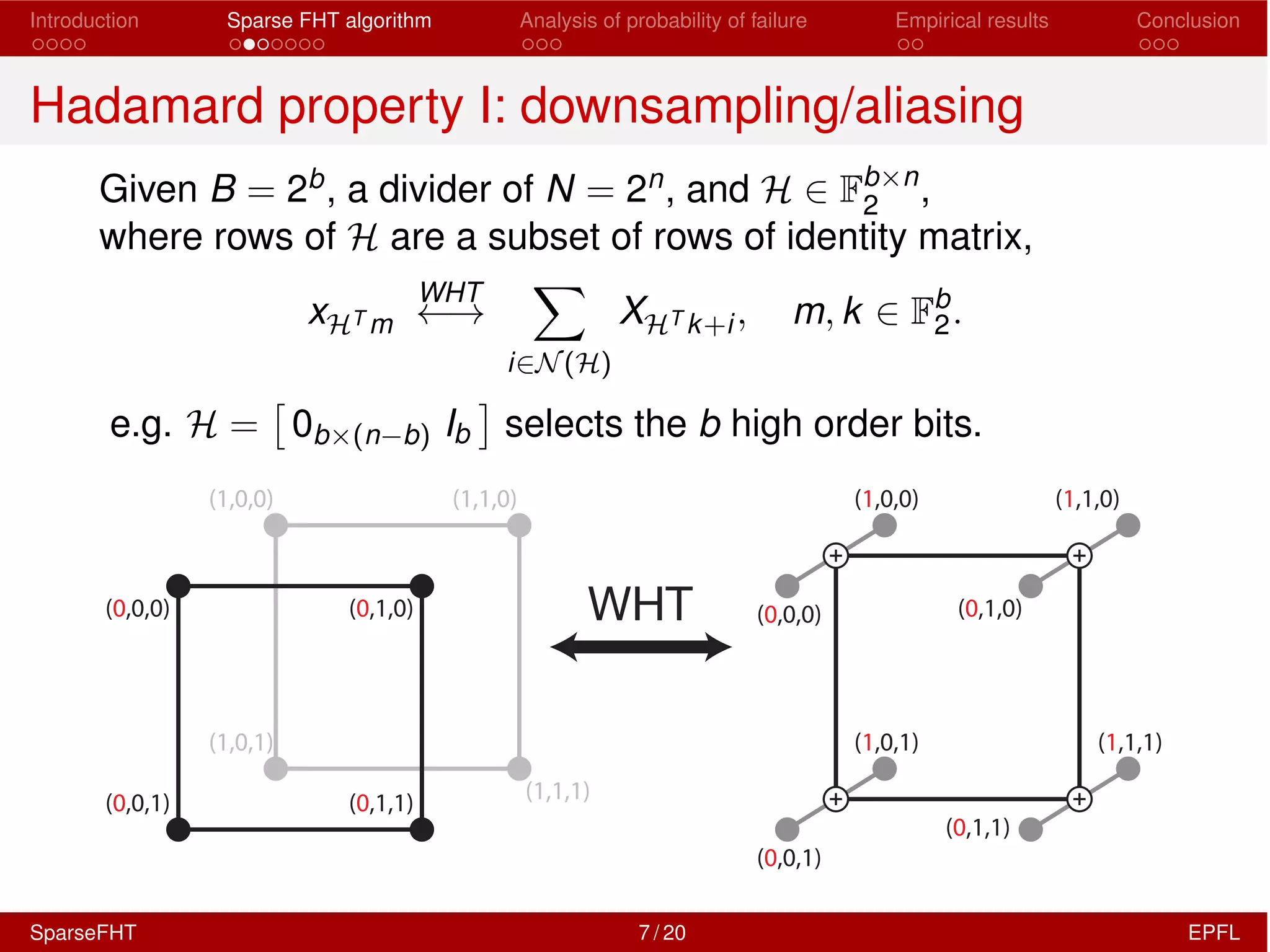
79. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
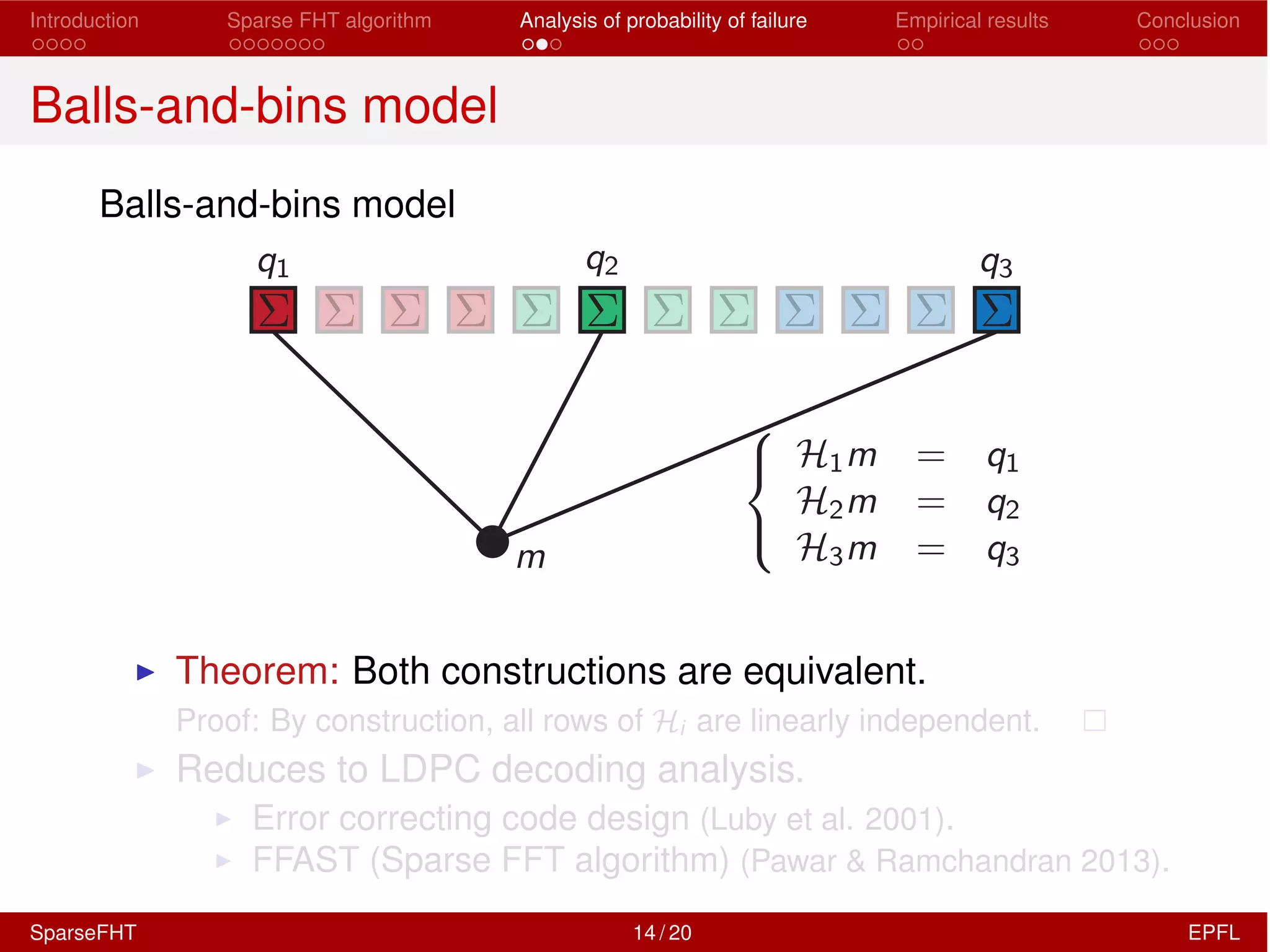
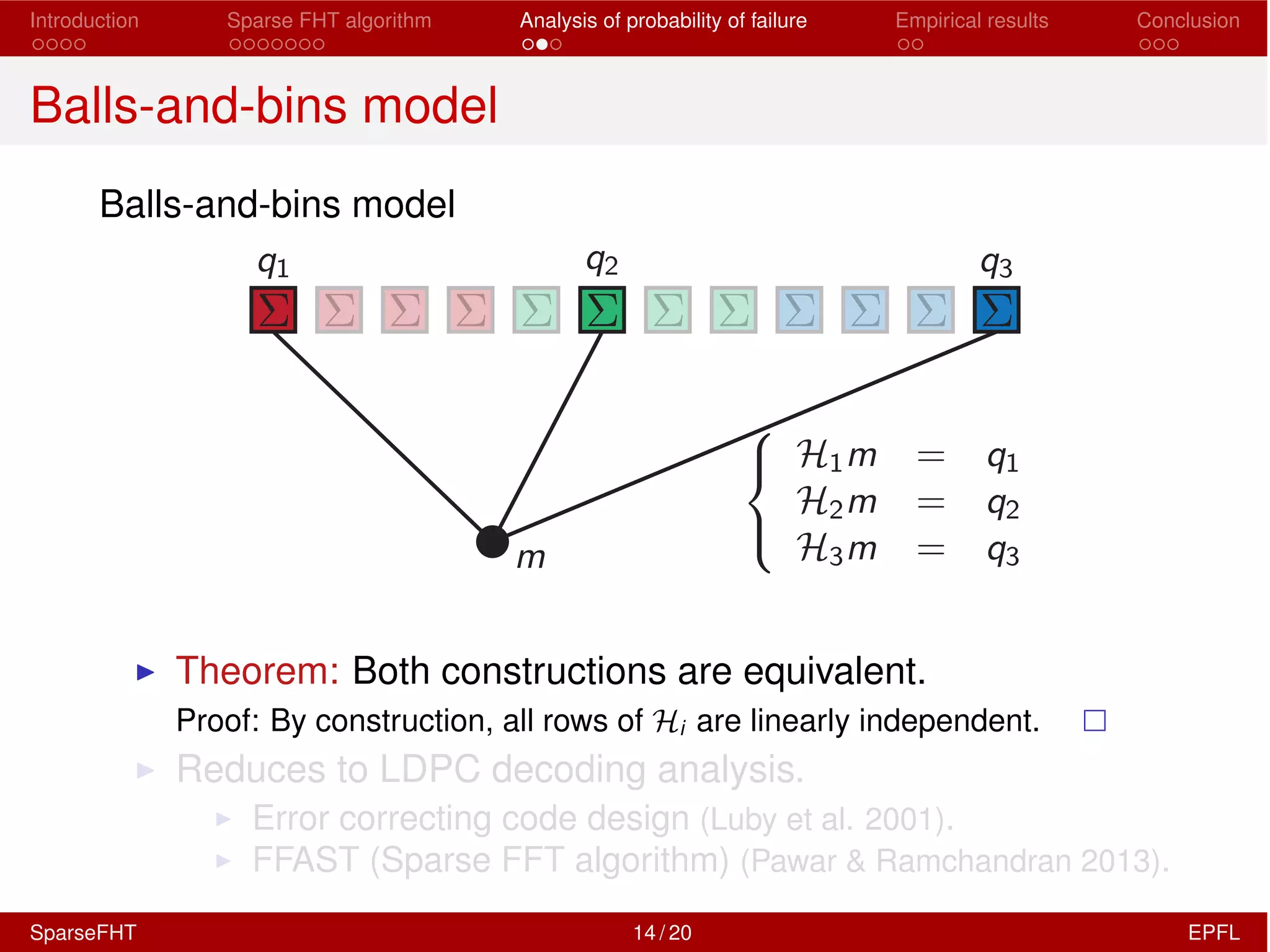
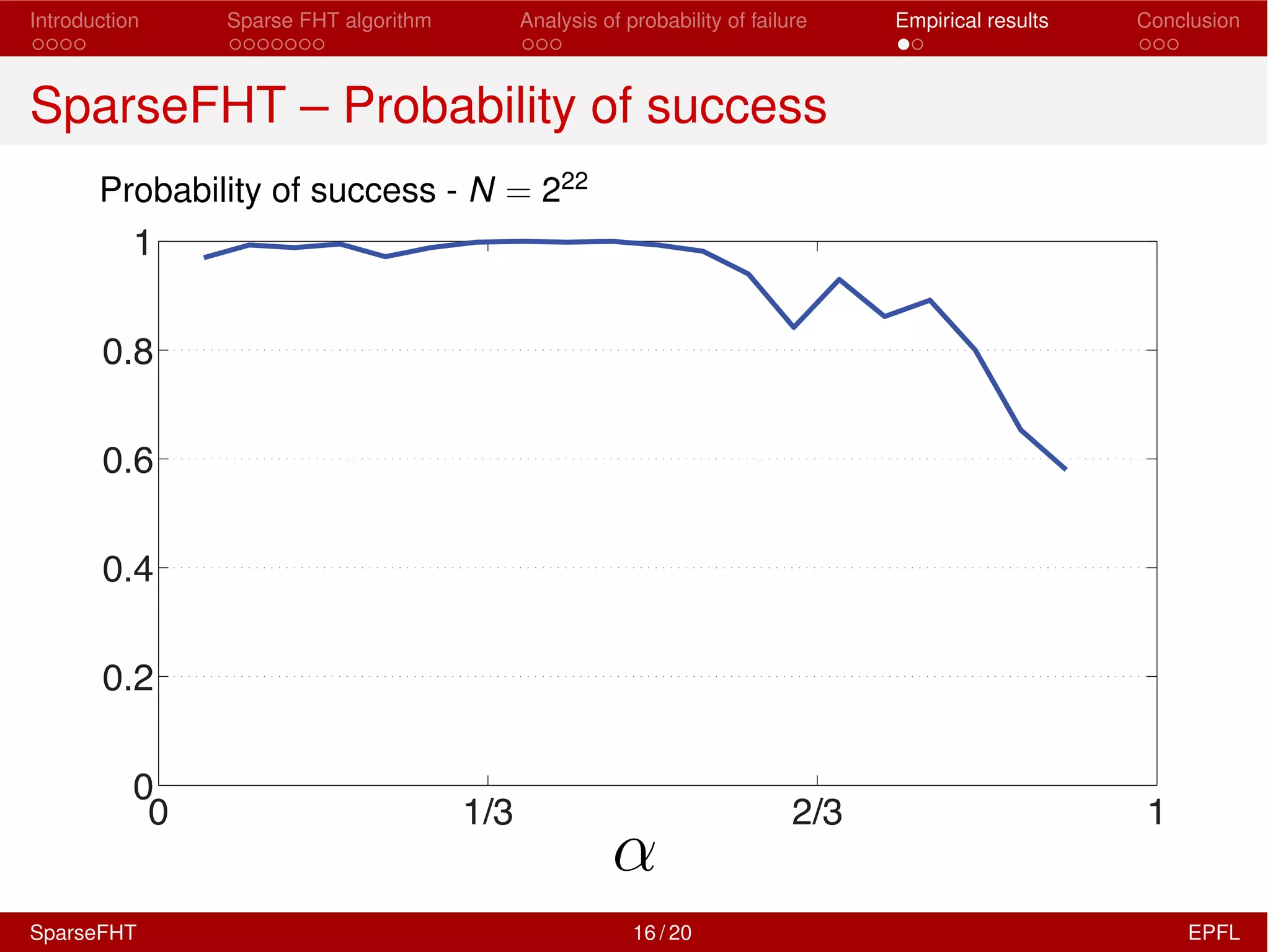
SparseFHT vs. FHT
Runtime [µs] – N = 215
0 1/3 2/3 1
0
200
400
600
800
1000
Sparse FHT
FHT
↵
SparseFHT 17 / 20 EPFL

80. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Conclusion
Contribution
I Sparse fast Hadamard algorithm.
I Time complexity O(K log2 K log2
N
K ).
I Sample complexity O(K log2
N
K ).
I Probability of success asymptotically equal to 1.
What’s next ?
I Investigate noisy case.
SparseFHT 18 / 20 EPFL

81. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Conclusion
Contribution
I Sparse fast Hadamard algorithm.
I Time complexity O(K log2 K log2
N
K ).
I Sample complexity O(K log2
N
K ).
I Probability of success asymptotically equal to 1.
What’s next ?
I Investigate noisy case.
SparseFHT 18 / 20 EPFL

82. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Thanks for your attention!
Code and figures available at
http://lcav.epfl.ch/page-99903.html
SparseFHT 19 / 20 EPFL

83. Introduction Sparse FHT algorithm Analysis of probability of failure Empirical results Conclusion
Reference
[1] M.G. Luby, M. Mitzenmacher, M.A. Shokrollahi, and
D.A. Spielman,
Efficient erasure correcting codes,
IEEE Trans. Inform. Theory, vol. 47, no. 2,
pp. 569–584, 2001.
[2] S. Pawar and K. Ramchandran,
Computing a k-sparse n-length discrete Fourier transform
using at most 4k samples and O(k log k) complexity,
arXiv.org, vol. cs.DS. 04-May-2013.
SparseFHT 20 / 20 EPFL