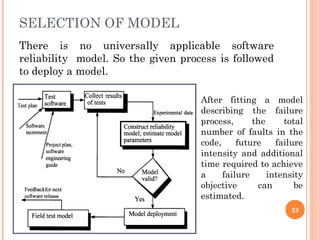
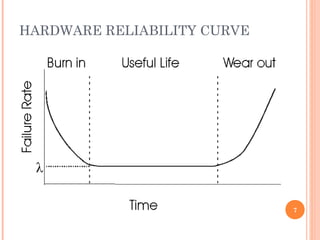
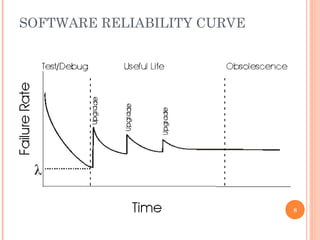
This document provides an overview of a seminar on software reliability modeling. The seminar covers topics such as what software reliability is, software failure mechanisms, measuring software reliability, software reliability models, and statistical testing. It discusses concepts like the difference between hardware and software reliability curves. It also summarizes various software reliability models and challenges in software reliability modeling.

1. A
SEMINAR
ON
SOFTWARE RELIABILITY MODELING
By:
Poonam Panwar
Regd. No. 951011002
Under The Supervision of:
Dr. Arvind Kumar Lal
Associate Professor
School of Mathematics & Computer Applications
Thapar University, Patiala-147004 (Punjab)

2. TOPICS COVERED
 What is Software Reliability?
 Software Failure Mechanisms
 Hardware vs Software
 Measuring Software Reliability
 Software Reliability Models
 Statistical Testing
 Conclusion
2

3. WHAT IS SOFTWARE RELİABİLİTY?
 Precisely it may be defined as a product’s
trustworthiness or dependability.
 The probability of failure-free software operation for a
specified period of time in a specified environment.
 Probability of the product working “correctly” over a
given period of time in a specified environment.
3

4. AREAS OF S/W RELIABILITY
 Software Reliability Modeling
 Prediction Analysis
 Reliability Measurement
 Defect Classification
 Trend Analysis
 Field Data Analysis
 Software Metrics
 Software Testing and Reliability
 Fault-Tolerance
 Fault Trees
 Software Reliability Simulation
 Software Reliability Tools
4

5. SOFTWARE CHARACTERISTICS
 Failure cause: Software defects are mainly design defects.
 Wear-out: Software does not have wear-out phase.
 Repairable system concept: Periodic restarts can help fix
software problems.
 Time dependency and life cycle: Software reliability is not a
function of operational time.
 Environmental factors: Do not affect Software reliability, except
it might affect program inputs.
 Reliability prediction: Software reliability can not be predicted
from any physical basis, since it depends completely on human
factors in design.
 Redundancy: Can not improve Software reliability if identical
software components are used.
 Interfaces: Software interfaces are purely conceptual rather
visual.
 Built with standard components: Well-understood and
extensively-tested standard parts will help improve
maintainability and reliability. But in software industry, this trend
is not observed. Code reuse has been around for some time, but to a
very limited extent. Strictly speaking there are no standard parts
for software, except some standardized logic structures.
5

6. SOFTWARE FAİLURE MECHANİSMS
 Design Faults: Software faults are mainly design faults
which are harder to visualize, classify, detect, and correct.
 Interfaces: Software can fail if interfaces are not correct.
(Interfaces are conceptual rather than visual in case of
software.)
 Errors, Ambiguities, Oversights or Misinterpretation
in the software requirement specification.
 Carelessness or Incompetence in writing code.
 Inadequate testing.
 Incorrect or Unexpected usage of the software.
 Other unforeseen problems.
6

7. HARDWARE RELIABILITY CURVE
7

8. SOFTWARE RELIABILITY CURVE
8

9. MEASURİNG SOFTWARE
RELİABİLİTY
 Current approaches for measuring software reliability are
basically parallel to those used for hardware reliability
assessment with appropriate modifications in account for
the inherent differences between software and hardware.
 A number of Software reliability models have been
proposed to address the problem of software reliability
measurement. These approaches are based mainly on the
failure history of software and can be classified according to
the nature of the failure process.
 Assessed value of the software reliability measure is always
relative to a given use environment. Two users exercising
two different sets of paths in the same software are likely to
have different values of software reliability.
 Measuring software reliability remains a difficult problem
because we don't have a good understanding of the nature
of software. 9

10. o Transient: Transient failures occur only for
certain inputs.
o Permanent: Permanent failures occur for all
input values.
o Recoverable: When recoverable failures occur
the system recovers with or without operator
intervention.
o Unrecoverable: the system may have to be
restarted.
o Cosmetic: May cause minor irritations. Do not
lead to incorrect results. Eg. mouse button has to
be clicked twice instead of once to invoke a GUI
function.
FAİLURE CLASSES
10

11. SOFTWARE RELİABİLİTY
MODELING TECHNIQUES
 Software reliability modeling techniques
can be divided into two subcategories:
Prediction Modeling
Estimation Modeling.
 Both kinds of modeling techniques are
based on observing and accumulating
failure data and analyzing with statistical
inference.
11

12. COMPARISON OF SOFTWARE
RELİABİLİTY MODELING TECHNIQUES
ISSUES PREDICTION MODELS ESTIMATION MODELS
DATA REFERENCE Uses historical data Uses data from the
current software
development effort
WHEN USED IN
DEVELOPMENT
CYCLE
Usually made prior to
development or test
phases; is available as
early as concept phase
Usually made later in life
cycle(after some data
have been collected);
cannot be used in
concept or development
phases
TIME FRAME Predict reliability for
future time.
Estimate reliability at
either present or future
time

13. SOFTWARE RELİABİLİTY MODELS
 A software reliability model specifies the form of a
random process that describes the behavior of
software failures with respect to time.
 Software reliability models have emerged as
people try to understand the characteristics of how
and why software fails, and try to quantify
software reliability.
 Over 200 models have been developed since the
early 1970s, but how to quantify software
reliability still remains largely unresolved.
 There is no single model that can be used in all
situations. No model is complete or even
representative.
13

14. CATEGORIES OF SOFTWARE
RELIABILITY MODELS WITH KEY
ASSUMPTIONS
 Times Between Failures (TBF) Models
* Independent times between failures.
* Equal probability of the exposure of each fault.
* Embedded faults are independent of each other.
* Faults are removed after each occurrence.
* No new faults introduced during correction, i.e., perfect fault removal.
 Fault Count (FC) Models
* Testing intervals are independent of each other.
* Testing during intervals is reasonably homogeneous.
* Numbers of faults detected during non overlapping intervals are
independent of each other.
 Fault Seeding (FS) Models
* Seeded faults are randomly distributed in the program.
* Indigenous and seeded faults have equal probabilities of being detected.
 Input Domain Based (IDB) Models
* Input profile distribution is known.
* Random testing is used.
* Input domain can be partitioned into equivalent classes. 14

15. SOFTWARE RELIABILITY MODELS
15

16. 16

17. 17

18. COMPONENTS OF A SOFTWARE
RELİABİLİTY MODEL
 Most software models contain the
following parts:
Assumptions,
Factors,
A mathematical function which relates
the reliability with the factors, which is
usually a higher order exponential or
logarithmic function.
18

19. SOME WELL KNOWN SOFTWARE
RELIABILITY MODELS
 Jelinsky and Moranda Model
 Basic Execution Time Model
 Logarithmic Poisson Time Model
 The Bug Seeding Model
 Shooman Model
 Littlewood-Verrall Model
 Goel-Okumoto Model
 Musa-Okumoto Model
19

20. This model is the earliest and probably the best known
reliability model. It proposed a failure intensity function
in the form:
λ(t)=φ(N-i+1)
Where
φ= constant of proportionality
N= total number of errors present
i= number of errors found by time interval ti
In this model each time an error is repaired reliability
does not increase by a constant amount.
Reliability improvement due to fixing of an error is
assumed to be proportional to the number of errors
present in the system at that time.
JELINSKI AND MORANDA MODEL
20

21. BASIC EXECUTION TIME MODEL
 This model was developed by J.D. Musa in 1979 and is
based on execution time.
 In this model, the decrease in failure intensity, as a
function of the number of failures observed, is
constant and is given as:
 Where λo: Initial Failure Intensity
 Vo: Number of failures experienced, if a program is
executed for infinite time period.
 µ: Average or expected number of failures experienced
at a given period of time.
 τ: execution time.
21

22. LOGARITHMIC POISSON TIME
MODEL
 This model is also developed by Musa et. al.
[MUSA79].
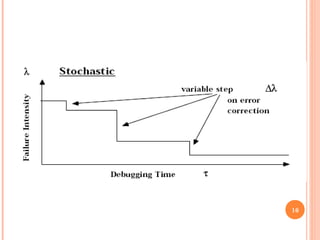
 The failure intensity function is different here as
compared to basic model. In this case the failure
intensity function decreases exponentially whereas it is
constant for basic model.
λ(µ)= λo exp(-θ µ)
Where
θ: called the failure intensity decay parameter. (represents the
relative change of failure intensity per failure experienced)
 The expected number of failures for this model is
always infinite at infinite time.
 At larger value of execution time, the logarithmic
poison time model will have larger value of failure
intensity than the basic model.
22

23. There is no universally applicable software
reliability model. So the given process is followed
to deploy a model.
SELECTION OF MODEL
After fitting a model
describing the failure
process, the total
number of faults in the
code, future failure
intensity and additional
time required to achieve
a failure intensity
objective can be
estimated.
23

24. UNCERTAINTIES IN SOFTWARE
RELİABİLİTY MODELING
TECHNIQUES
 There are two main types of uncertainties
which render any reliability measurement
inaccurate:
 Type 1 Uncertainty:
 our lack of knowledge about how the system will be
used, i.e. its operational profile
 Type 2 Uncertainty:
 reflects our lack of knowledge about the effect of
fault removal.
 When we fix a fault we are not sure if the corrections are
complete and successful and no other faults are
introduced
 Even if the faults are fixed properly we do not know how
much will be the improvement to inter-failure time. 24

25. STATİSTİCAL TESTİNG
 Statistical testing is a technique in which a
model of the statistical distribution of the input
is used to construct representative test cases.
 The objective of statistical testing is to determine
reliability rather than discover errors.
 It is different from defect testing.
 Different users have different operational profile
i.e. they use the system in different ways
(formally, operational profile).
 In statistical testing the input data is divided
into a number of input classes e.g. create, edit,
print, file operations, etc.
25

26. PERFORMING A STATISTICAL TEST
 Determine the operational profile of the software:
This can be determined by analyzing the usage
pattern.
 Manually select or automatically generate a set
of test data:
corresponding to the operational profile.
 Apply test cases to the program:
record execution time between each failure
it may not be appropriate to use raw execution
time
 After a statistically significant number of failures
have been observed:
reliability can be computed. 26

27. CONCLUSİONS
 Software reliability is a key part in
software quality.
 Software reliability improvement is hard.
 There are no generic models.
 Measurement is very important for
finding the correct model.
 Statistical testing should be used but it is
not easy.
 Software Reliability Modelling is not
simple.
27

28. 1. Jintao Zeng, Jinzhong Li, Xiaohui Zeng, Wenlang Luo “A Prototype System of
Software Reliability Prediction and estimation” ,third International
symposium on Intelligent Information Technology and Security Informatics by
IEEE Computer Society, 2010.
2. Michael R. Lyu “Software Reliability Engineering: A Roadmap”, Future of
Software Engineering(FOSE’07) by IEEE, 2007.
3. Bing Chao, XiaoDong Zhu, Qiang Li, AnCe Huang “ Reliability Management
in Software Requirement Analysis”, IEEE International Conference on
Management of Innovation and Technology, 2006.
4. Rajesh Kumar Bawa, Arvind Kumar Lal and Navdeep Singh Jaggi “A Model
for Analysis of Software Reliability and Availability”, Proceedings of RPN
March 2004.
5. K K Aggarwal & Yogesh Singh “Software Engineering” 3rd
Edition, New Age
International Publishers, 2008.
6. Michael R. Lyu “Handbook of Software Reliability Engineering”, Computer
Society Press, 2006.
7. J.D. Musa “Software Reliability Engineering: More Reliable Software Faster
and Cheaper” 2nd Edition, AuthorHouse, 2004 .
8. K. S. Trivedi “Probability and Statistics with Reliability, Queuing and
Computer Science Applications” 2nd Edition, John Wiley and Sons, 2002.
References:
28