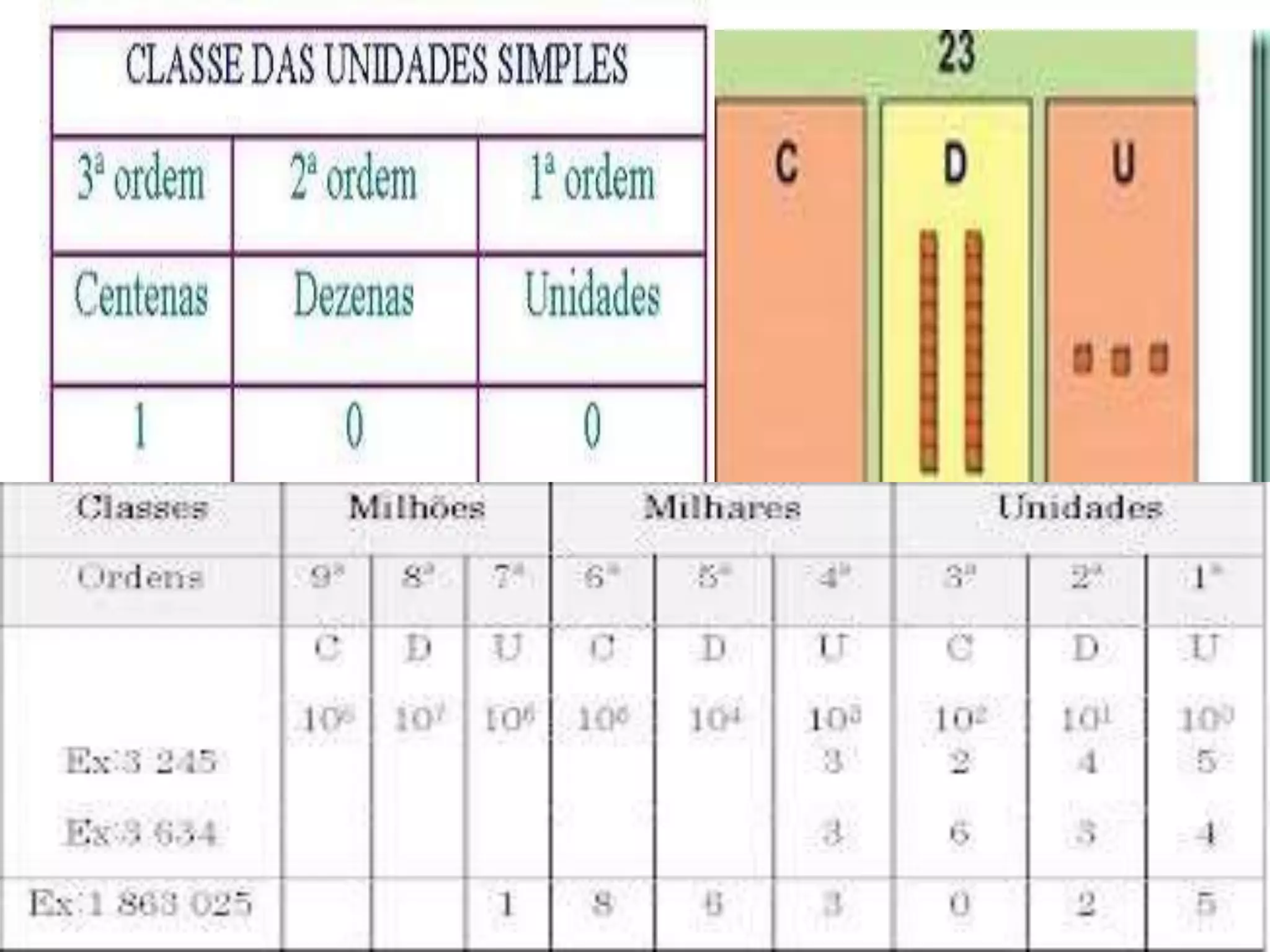
1) O documento discute o sistema de numeração decimal, que é o tipo de representação numérica usado atualmente e é organizado na base 10. 2) Uma característica importante é ser posicional, onde o valor de cada algarismo depende de sua posição, com cada posição determinando uma multiplicação por uma potência de 10. 3) O documento ressalta a importância de trabalhar as características do sistema de numeração decimal na educação matemática escolar.

1. Sistema de
numeração decimal

3. Sistema de numeração decimal é o tipo
de representação que usamos hoje para
expressar quantidades, medidas e
códigos (o número da conta corrente do
banco, por exemplo) e para realizar
operações. Tem esse nome por ser
organizado na base 10 - de origem
provavelmente ligada às contagens que
os homens primitivos faziam com os dez
dedos das mãos.

4. Uma importante característica do sistema
decimal é o fato de ele ser posicional.
Isso significa que o valor de cada
algarismo depende do lugar que ele
ocupa na escrita. Partindo da primeira
casa, da direita para a esquerda, cada
posição determina a multiplicação do
algarismo por uma potência de 10
(0, 10, 100, 1000...).

6. • No sistema decimal, o número 317, por
exemplo, é a composição de 3 x 10² + 1 x 10¹ +
7 x 10°. Essa lógica multiplicativa e aditiva
resulta em um meio econômico de escrita
numérica, pois com poucas notações é
possível escrever números grandes.

9. Trabalhar as características do sistema é a
chave para fazer os alunos avançarem em
Matemática
O sistema de numeração decimal é um elemento
essencial da formação matemática escolar. ''Esse
conteúdo atravessa todos os anos da escolaridade
básica'', explica Fernanda Penas, especialista argentina
em didática da Matemática. É
fundamental, portanto, que as crianças compreendam
a lógica do sistema e saibam que os números existem
para registrar quantidades, para compará-las, para
ordenar itens contados, para identificar objetos por
meio de códigos, para antecipar ações não realizadas
com operações e, também, para realizar as operações

11. • 3.1 Ordenação de números
• 3.2 Comparação, interpretação e produção de
números
• 3.3 Busca de regularidades
• 3.4 Relação com operações aritméticas

12. • Na prática pedagógica, o trabalho com a
relação de ordem dos números é necessário
para mostrar à turma a forma de organização
do sistema, em base dez e com valor
posicional.
• Quando compreendem a característica
posicional do sistema, as crianças conseguem
ordenar valores, mesmo os mais altos

13. • 3.1 Ordenação de números
• 3.2 Comparação, interpretação e produção de
números
• 3.3 Busca de regularidades
• 3.4 Relação com operações aritméticas

14. • Medir e ordenar as alturas das crianças ou anotar
os preços de um mesmo produto em diferentes
panfletos de supermercado, do mais barato ao
mais caro, são exemplos de propostas de
comparação, produção e interpretação.
• Processos simples, como procurar uma casa na
rua pela numeração, são desafiadores para os
pequenos. Nesse exemplo, ao mesmo tempo em
que descobrem como os números indicam a
localização da casa, eles podem ser incentivados
a escrever esses valores, mesmo que o façam de
forma diferente da notação convencional.

15. • 3.1 Ordenação de números
• 3.2 Comparação, interpretação e produção de
números
• 3.3 Busca de regularidades
• 3.4 Relação com operações aritméticas

16. • Ao realizar atividades de comparação, produção e
interpretação de números, as crianças criam
hipóteses sobre as regularidades do sistema de
numeração decimal. Para comparar dois
números, é necessário algum tipo de critério
e, para produzir e interpretá-los, são pensados
argumentos que fundamentam ou rejeitam as
escritas numéricas.
• Essa busca de regularidades apresenta dois eixos
desafiadores: as regras da escrita de números e
as regras da numeração oral. Embora esses
conhecimentos estejam vinculados, é importante
lembrar que são diferentes

17. • 3.1 Ordenação de números
• 3.2 Comparação, interpretação e produção de
números
• 3.3 Busca de regularidades
• 3.4 Relação com operações aritméticas

18. • O sistema de numeração
decimal é a base para as
operações aritméticas.
Somamos, subtraímos, m
ultiplicamos e dividimos
de acordo com os
critérios do sistema de
valor posicional e base
10. Essa relação deve ser
considerada em classe
para que a turma consiga
avançar na manipulação
da tabela numérica