This document discusses various sorting and searching algorithms. It begins by listing sorting algorithms like selection sort, insertion sort, bubble sort, merge sort, and radix sort. It then discusses searching algorithms like linear/sequential search and binary search. It provides details on the implementation and time complexity of linear search, binary search, bubble sort, insertion sort, selection sort, and merge sort. Key points covered include the divide and conquer approach of merge sort and how binary search recursively halves the search space.

1. Chapter 2
Sorting and Searching Techniques
Course Outcome – Understand Concepts of searching and sorting

2. Syllabus
Sorting
 Selection sort
Insertion sort
 Bubble sort
 Merge sort
 Radix sort ( Only algorithm )
Shell sort ( Only algorithm )
 Quick sort ( Only algorithm )
Searching
Linear search
Binary search

3. Searching
• Searching is an operation or a technique that helps finds
the place of a given element or value in the list.
• Any search is said to be successful or unsuccessful
depending upon whether the element that is being
searched is found or not.
• Some of the standard searching technique that is being
followed in the data structure is listed below:
 Linear Search or Sequential Search
 Binary Search

4. Linear Search or Sequential Search
• This is the simplest method for searching.
• In this type of search, a sequential search is made over all
items one by one.
• Every item is checked and if a match is found then that
particular item is returned, otherwise the search continues till
the end of the data collection.
• This method can be performed on a sorted or an unsorted list
(usually arrays).

5. • The list given below is the list of elements in an unsorted
array. The array contains ten elements. Suppose the element
to be searched is ‘33', so 33 is compared with all the elements
starting from the 0th element, and the searching process ends
where 33 is found, or the list ends.
• The performance of the linear search can be measured by
counting the comparisons done to find out an element. The
number of comparison is 0(n).

6. #include<stdio.h>
void main ()
{
int a[10] = {10, 23, 40, 1, 2, 0, 14, 13, 50, 9};
int item, i,flag;
printf("nEnter Item which is to be searchedn");
scanf("%d",&item);
for (i = 0; i< 10; i++)
{
if(a[i] == item)
{
flag = i+1;
break;
}
else
flag = 0;
}
if(flag != 0)
{
printf("nItem found at location %dn",flag);
}
else
{
printf("nItem not foundn");
}
}

7. Complexity of algorithm
Complexity Best Case Average Case Worst Case
Time O(1) O(n) O(n)
Space O(1)

8. Binary Search
• While using this searching method array should be sorted
in increasing numerical order.
• Suppose DATA is an array, which is sorted in increasing
numerical order, and we want to find out the location LOC
of a given ITEM of information in DATA.
• Then the binary search algorithm applied works as follows.
During each search for ITEM is reduced to a segment of
elements of data:
DATA [BEG],DATA[BEG+1],DATA[BEG+2],…..DATA[END]
• Here BEG and END variables denoted beginning and end
locations of the segment under consideration.
• This algorithm compares ITEM with middle element
DATA[MID] of the segment where MID is obtained by
MID = INT [(BEG + END)/2]

9. If DATA [MID] = ITEM then the search is successful and we set
LOC:=MID
otherwise a new segment of DATA is obtained as follows,
a) If ITEM<DATA[MID] then item can appear in left half of
the segment.
DATA[BEG],DATA[BEG+1],…….DATA[MID-1]
So we reset END:=MID-1 and begin searching again
b)If ITEM>DATA[MID] then ITEM can appear only in the right
half of the segment.
DATA[mid+1],DATA[MID+2],…….DATA[END]
So we reset BEG :=MID+1 and begin searching again.
c)If ITEM is not in DATA then eventually we obtain END<BEG
It means that search is unsuccessful. In this case we assign
LOC: =NULL
(Generally we begin with BEG=1 AND END=N or more
generally we can say BIG=LB and END=UB)

10. 11 18 20 22 25 32 33 37 39 42 ITEM =20
LB(BEG) UB(END)
MID=INT[(BEG+END)/2]
= INT[(1+10)/2]
=INT[11/2] =INT[5.5]= 5
11 18 20 22 25 32 33 37 39 42
DATA[MID] ≠ ITEM 25 ≠ 20
ITEM < DATA[MID] 20 < 25 yes Set END:=MID-1
11 18 20 22
Set MID:= INT[(BEG+END)/2]= INT[(1+4)/2]=INT[2.5] = 2
11 18 20 22
data[MID]=ITEM 18=20 no Set BEG:=MID+1
20 22
MID= 3
data[MID]=ITEM 20=20 yes Set LOC:= MID
LOC= 3

11. 11 18 20 22 25 32 33 37 39 42 ITEM =37
LB(BEG) UB(END)
MID=INT[(BEG+END)/2]
= INT[(1+10)/2]
=INT[11/2] =INT[5.5]= 5
11 18 20 22 25 32 33 37 39 42
DATA[MID] ≠ ITEM 25 ≠ 37
ITEM < DATA[MID] 37 < 25 no Set BEG:=MID+1
32 33 37 39 42
Set MID:= INT[(BEG+END)/2]= INT[(6+10)/2]=8
32 33 37 39 42
data[MID]=ITEM 37=37 yes Set LOC:= MID
LOC= 8

12. #include <stdio.h>
int main()
{
int c, first, last, middle, n, search, array[100];
printf("Enter number of elementsn");
scanf("%d", &n);
printf("Enter %d integersn", n);
for (c = 0; c < n; c++)
scanf("%d", &array[c]);
printf("Enter value to findn");
scanf("%d", &search);
first = 0;
last = n - 1;
middle = (first+last)/2;
while (first <= last) {
if (array[middle] < search)
first = middle + 1;
else if (array[middle] == search) {
printf("%d found at location %d.n", search, middle+1);
break;
}
else
last = middle - 1;
middle = (first + last)/2;
}
if (first > last)
printf("Not found! %d isn't present in the list.n", search);
return 0;
}

13. Applications
• This algorithm used to search ordered way.
• To find out target element whether it is
present or not.
If present then correspondingly it gives
position in array.
Limitations
1. The given list must be sorted.
2. The access of list must be random means; the
middle element can be accessed.

14. Complexity of Binary Search
Algorithm
• The complexity is measured by number of f(n)
of comparisons to locate ITEM in DATA where
DATA contains n elements.
• Each comparison reduces sample size in half.
• So we require at most f(n) comparisons to
locate ITEM where
f(n)= [log2 n]+1

15. Sorting
• Sorting is a process of ordering or placing a
list of elements from a collection in some
kind of order.
• It is nothing but storage of data in sorted
order.
• Sorting can be done in ascending and
descending order.
• It arranges the data in a sequence which
makes searching easier.

16. Bubble Sorting
• Sorting means, rearranging the elements in
increasing or decreasing order.
• Suppose A[1], A[2],….A[n] are in memory.
• Working-
• Compare A[1] and A[2] and arrange them in
desired order, so that A[1] ,A[2].
• Then compare A[2] and A[3] and arrange them so
that A[2] ,A[3].
• Continue this process until we compare A[N-1]
with A[N] so that A[N-1],A[N].

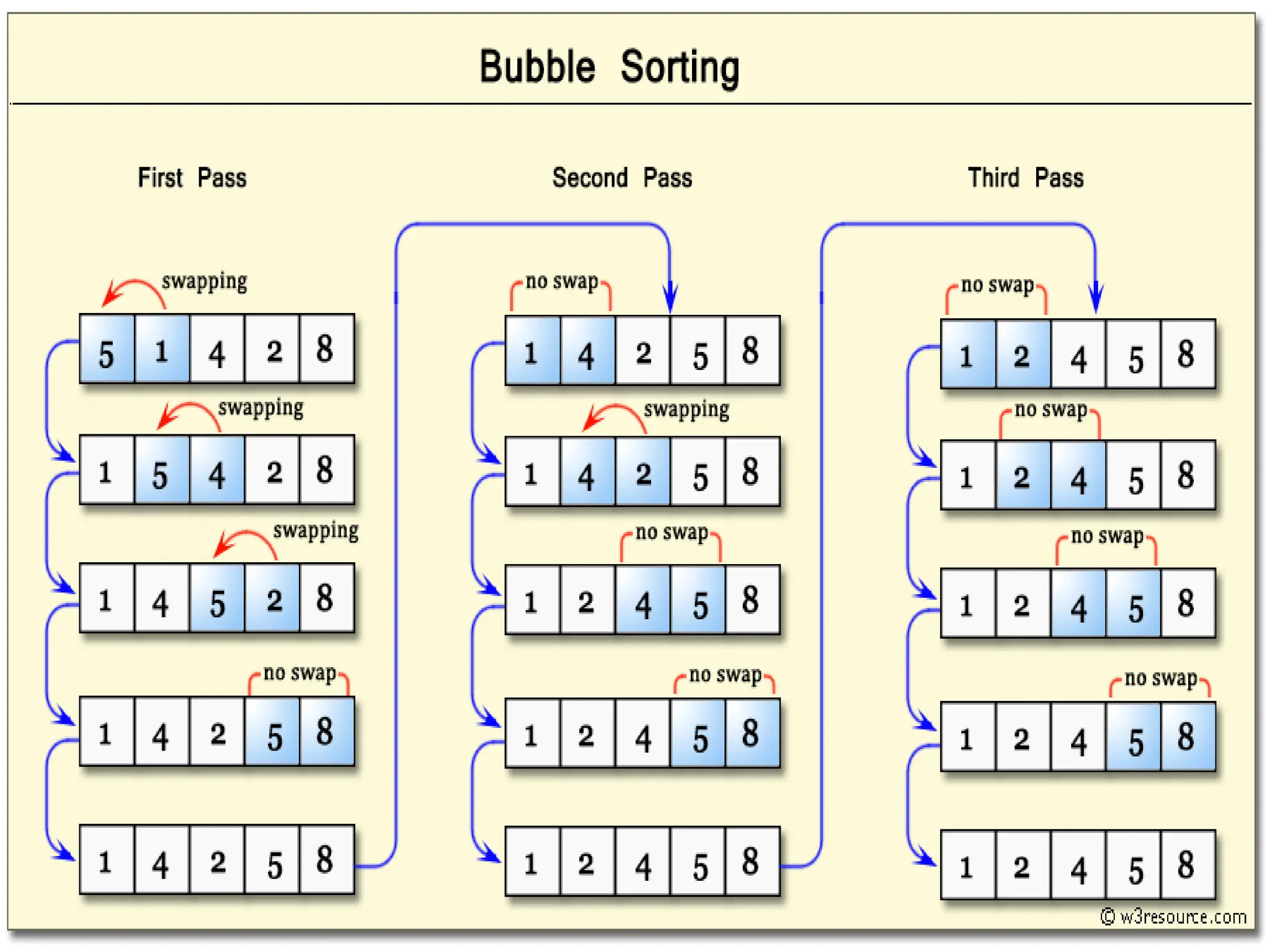
19. • Step 1: It involves n-1 comparisons. During this
step, the largest element is coming like a bubble
to the nth position. When step 1 is completed
A[N] will contain the largest element.
• Step 2: Repeat step 1 with one less comparison.
Step 2 involves n-2 comparisons, when step 2 is
completed we get second largest element A[N-2].
• Step 3: Repeat step 1 with two less comparisons.
It involves N-3 comparisons.
• Step N-1: Compare A[1] with A[2] and arrange
them so that A[1],A[2]. After n-1 steps the list will
be sorted in increasing order.

20. • Pass- The process of sequentially traversing through all
or part of a list is called a pass.
• The bubble sort algorithm requires N-1 passes where n
is number of input items.
• The time required for sorting algorithm is measured in
terms of comparisons. Specifically there are n-1
comparisons during first pass n-2 comparisons in
second pass and so on.
Complexity of algorithm-
f(n)=(n-1)+(n-2)+……..+2+1
=n(n-1)/2
= n2 /2 +o(n)
= o(n2)
The time required to execute bubble sort algorithm is
proportional to n2 where n is number of input items.

21. #include<stdio.h>
int main()
{
int count, temp, i, j, number[30];
printf("How many numbers are u going to enter?: ");
scanf("%d",&count);
printf("Enter %d numbers: ",count);
for(i=0;i<count;i++)
scanf("%d",&number[i]);
for(i=count-2;i>=0;i--)
{
for(j=0; j<=i; j++)
{
if(number[j]>number[j+1])
{
temp=number[j];
number[j]=number[j+1];
number[j+1]=temp;
}
}
}
printf("Sorted elements: ");
for(i=0;i<count;i++)
printf(" %d",number[i]);
return 0;
}

22. Insertion sort
• Insertion sort is a simple sorting algorithm that
works similar to the way you sort playing cards in
your hands. The array is virtually split into a
sorted and an unsorted part. Values from the
unsorted part are picked and placed at the
correct position in the sorted part.
• Insertion sort is the sorting mechanism where
the sorted array is built having one item at a
time. The array elements are compared with
each other sequentially and then arranged
simultaneously in some particular order.

24. • Step 1 - If the element is the first element, assume that
it is already sorted. Return 1.
• Step2 - Pick the next element, and store it separately in
a key.
• Step3 - Now, compare the key with all elements in the
sorted array.
• Step 4 - If the element in the sorted array is smaller
than the current element, then move to the next
element. Else, shift greater elements in the array
towards the right.
• Step 5 - Insert the value.
• Step 6 - Repeat until the array is sorted.

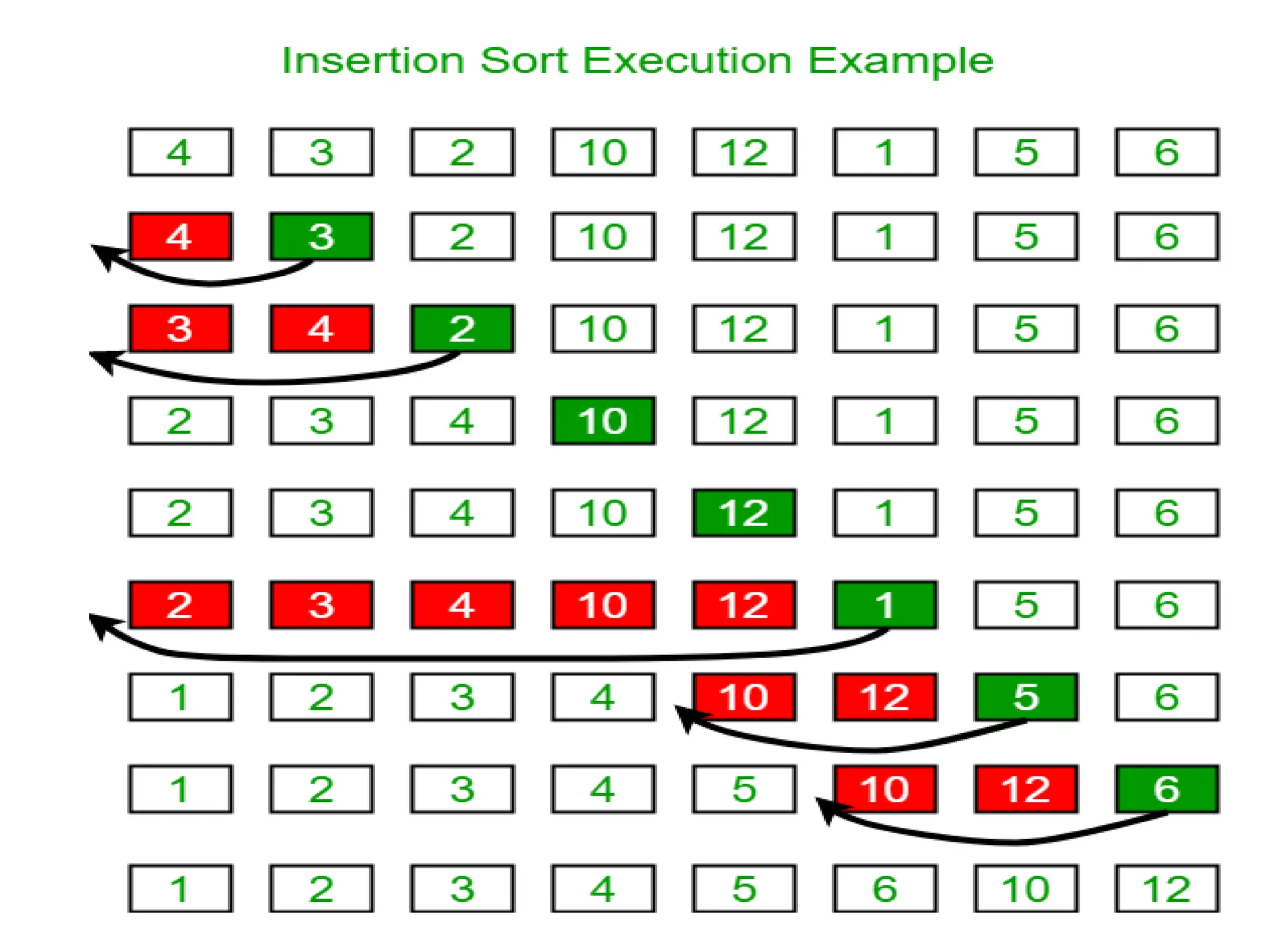
25. #include<stdio.h>
int main()
{
int i, j, count, temp, number[25];
printf("How many numbers u are going to enter?: ");
scanf("%d",&count);
printf("Enter %d elements: ", count);
for(i=0;i<count;i++)
scanf("%d",&number[i]);
for(i=1; i<count; i++)
{
temp=number[i];
j=i-1;
while((temp<number[j])&&(j>=0))
{
number[j+1]=number[j];
j=j-1;
}
number[j+1]=temp;
}
printf("Order of Sorted elements: ");
for(i=0;i<count;i++)
printf(" %d",number[i]);
return 0;
}

26. Time Complexity
• Best Case Complexity - It occurs when there is no sorting required, i.e.
the array is already sorted. The best-case time complexity of insertion
sort is O(n).
• Average Case Complexity - It occurs when the array elements are in
jumbled order that is not properly ascending and not properly
descending. The average case time complexity of insertion sort
is O(n2).
• Worst Case Complexity - It occurs when the array elements are
required to be sorted in reverse order. That means suppose you have
to sort the array elements in ascending order, but its elements are in
descending order. The worst-case time complexity of insertion sort
is O(n2).
Space Complexity
The space complexity of insertion sort is O(1). It is because, in insertion
sort, an extra variable is required for swapping.

27. Selection sort
• In selection sort, the smallest value among the unsorted
elements of the array is selected in every pass and inserted
to its appropriate position into the array.
• It is an in-place comparison sorting algorithm.
• In this algorithm, the array is divided into two parts, first is
sorted part, and another one is the unsorted part.
• Initially, the sorted part of the array is empty, and unsorted
part is the given array.
• Sorted part is placed at the left, while the unsorted part is
placed at the right.
• In selection sort, the first smallest element is selected from
the unsorted array and placed at the first position.
• After that second smallest element is selected and placed
in the second position.
• The process continues until the array is entirely sorted.

29. Time Complexity
• Best Case Complexity - It occurs when there is no sorting
required, i.e. the array is already sorted. The best-case time
complexity of selection sort is O(n2).
• Average Case Complexity - It occurs when the array
elements are in jumbled order that is not properly
ascending and not properly descending. The average case
time complexity of selection sort is O(n2).
• Worst Case Complexity - It occurs when the array elements
are required to be sorted in reverse order. That means
suppose you have to sort the array elements in ascending
order, but its elements are in descending order. The worst-
case time complexity of selection sort is O(n2).
Space Complexity
The space complexity of selection sort is O(1). It is because, in
selection sort, an extra variable is required for swapping.

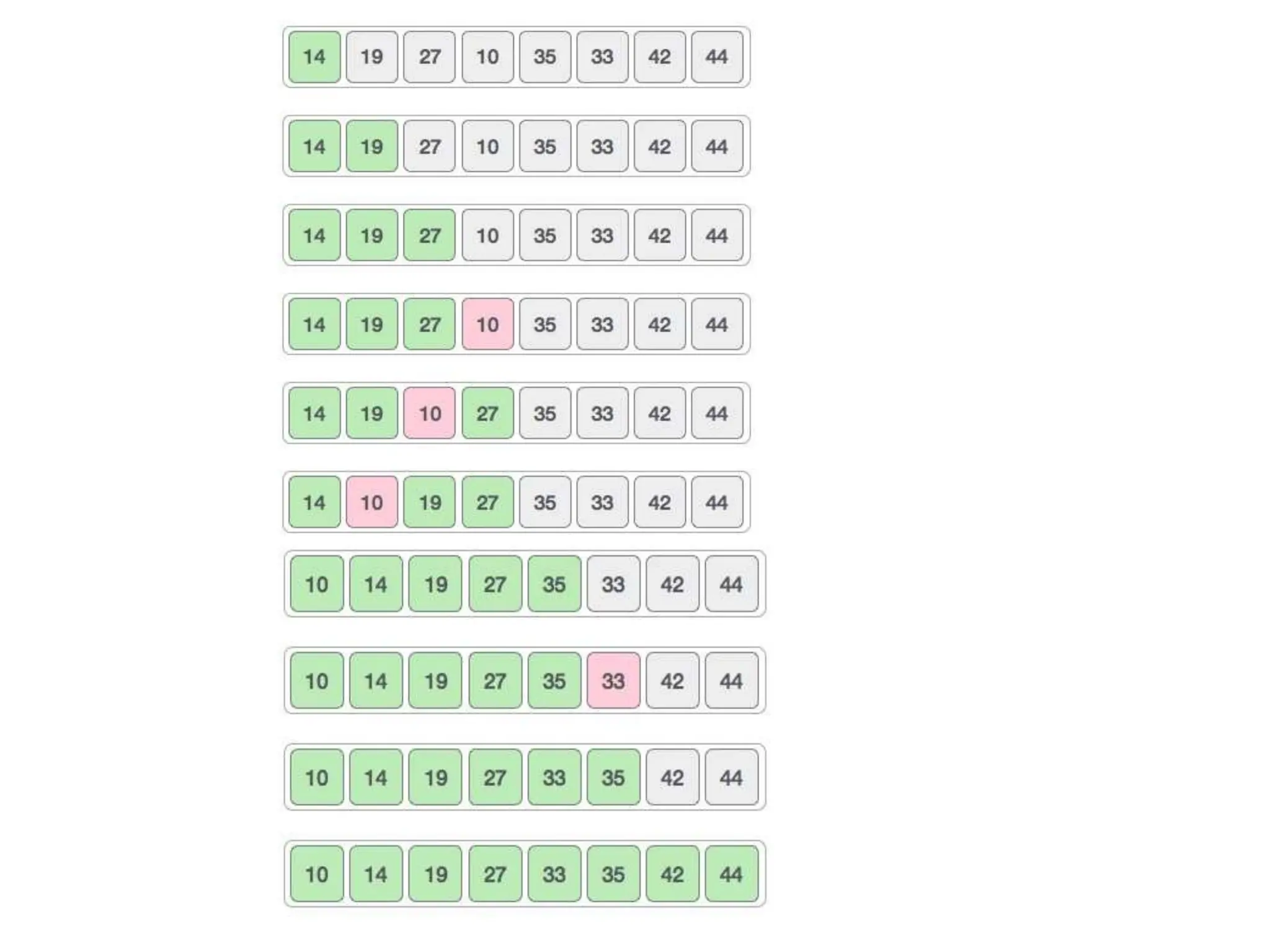
30. #include<stdio.h>
int main()
{
int i, j, count, temp, number[25];
printf("How many numbers u are going to enter?: ");
scanf("%d",&count);
printf("Enter %d elements: ", count);
for(i=0;i<count;i++)
scanf("%d",&number[i]);
for(i=0;i<count;i++)
{
for(j=i+1;j<count;j++)
{
if(number[i]>number[j])
{
temp=number[i];
number[i]=number[j];
number[j]=temp;
}
}
}
printf("Sorted elements: ");
for(i=0;i<count;i++)
printf(" %d",number[i]);
return 0;
}

31. Merge sort
• Merge sort is the algorithm which follows divide and
conquer approach. Consider an array A of n number of
elements.
• The algorithm processes the elements in 3 steps.
1. If A Contains 0 or 1 elements then it is already sorted,
otherwise, Divide A into two sub-array of equal
number of elements.
2. Conquer means sort the two sub-arrays recursively
using the merge sort.
3. Combine the sub-arrays to form a single final sorted
array maintaining the ordering of the array.

33. Complexity
• The time complexity of MergeSort is
O(n*Log n)
in all the 3 cases (worst, average and best)
as the merge sort always divides the array into
two halves and takes linear time to merge two
halves.
• Space Complexity= O(n)

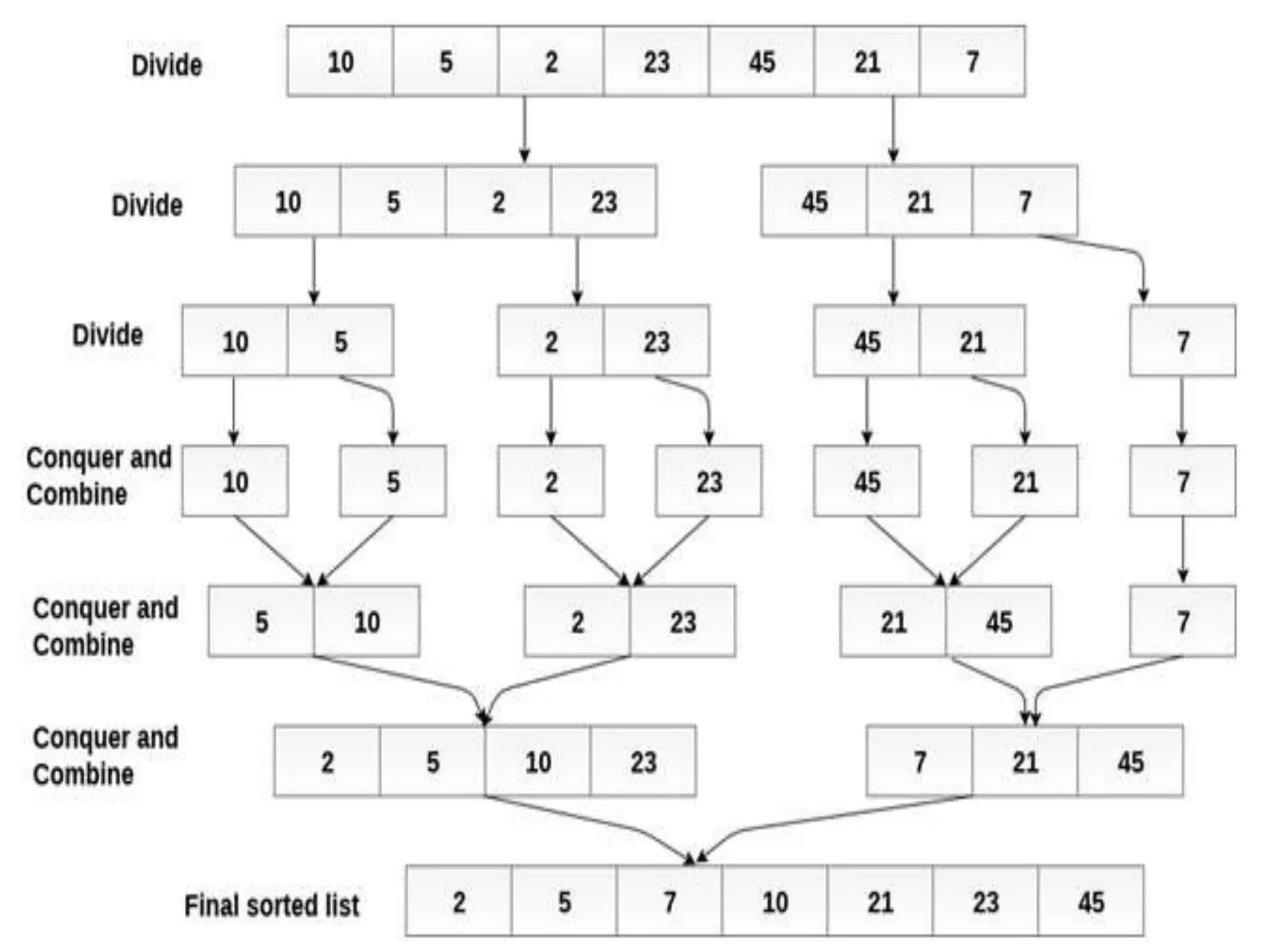
34. #include<stdio.h>
void mergeSort(int[],int,int);
void merge(int[],int,int,int);
void main ()
{
int a[8]= {10, 5, 2, 23, 45, 21, 7};
int i;
mergeSort(a,0,6);
printf("printing the sorted elements");
for(i=0;i<7;i++)
{
printf("n%dn",a[i]);
}
}
void mergeSort(int a[], int beg, int end)
{
int mid;
if(beg<end)
{
mid = (beg+end)/2;
mergeSort(a,beg,mid);
mergeSort(a,mid+1,end);
merge(a,beg,mid,end);
}
}

35. void merge(int a[], int beg, int mid, int end)
{
int i=beg,j=mid+1,k,index = beg;
int temp[7];
while(i<=mid && j<=end)
{
if(a[i]<a[j])
{
temp[index] = a[i];
i = i+1;
}
else
{
temp[index] = a[j];
j = j+1;
}
index++;
}
if(i>mid)
{
while(j<=end)
{
temp[index] = a[j];
index++;
j++;
}
}
else
{
while(i<=mid)
{
temp[index] = a[i];
index++;
i++;
}
}
k = beg;
while(k<index)
{
a[k]=temp[k];
k++;
}
}

36. Quick Sort
Quick sort is a sorting algorithm based on the divide and conquer
approach where
1. An array is divided into subarrays by selecting a pivot element
(element selected from the array).
While dividing the array, the pivot element should be positioned in
such a way that elements less than pivot are kept on the left side
and elements greater than pivot are on the right side of the pivot.
2. The left and right subarrays are also divided using the same
approach.
This process continues until each subarray contains a single
element.
3. At this point, elements are already sorted. Finally, elements are
combined to form a sorted array.

37. There are many different versions of quick Sort
that pick pivot in different ways.
• Always pick first element as pivot.
• Always pick last element as pivot
• Pick a random element as pivot.
• Pick median as pivot.

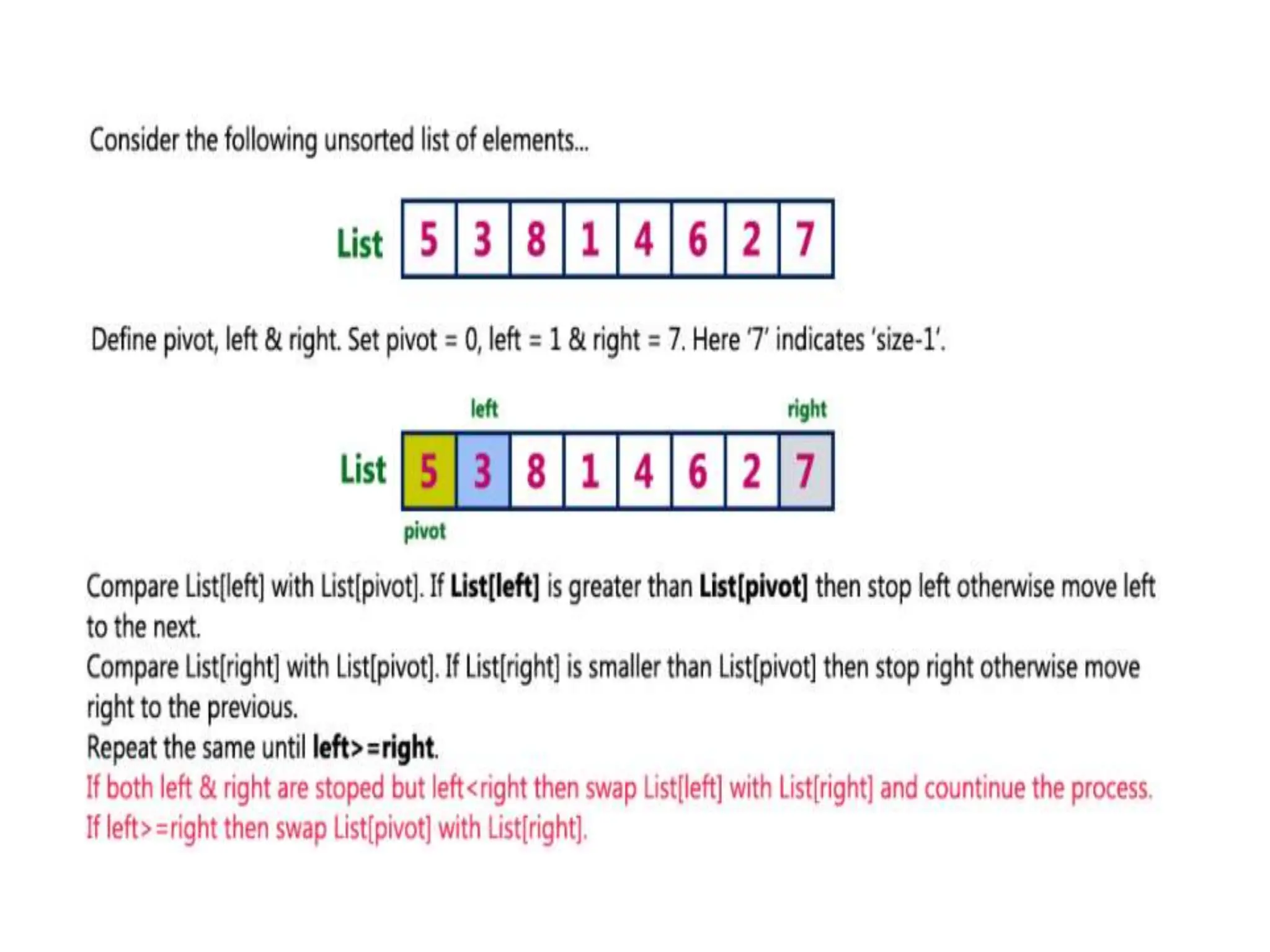
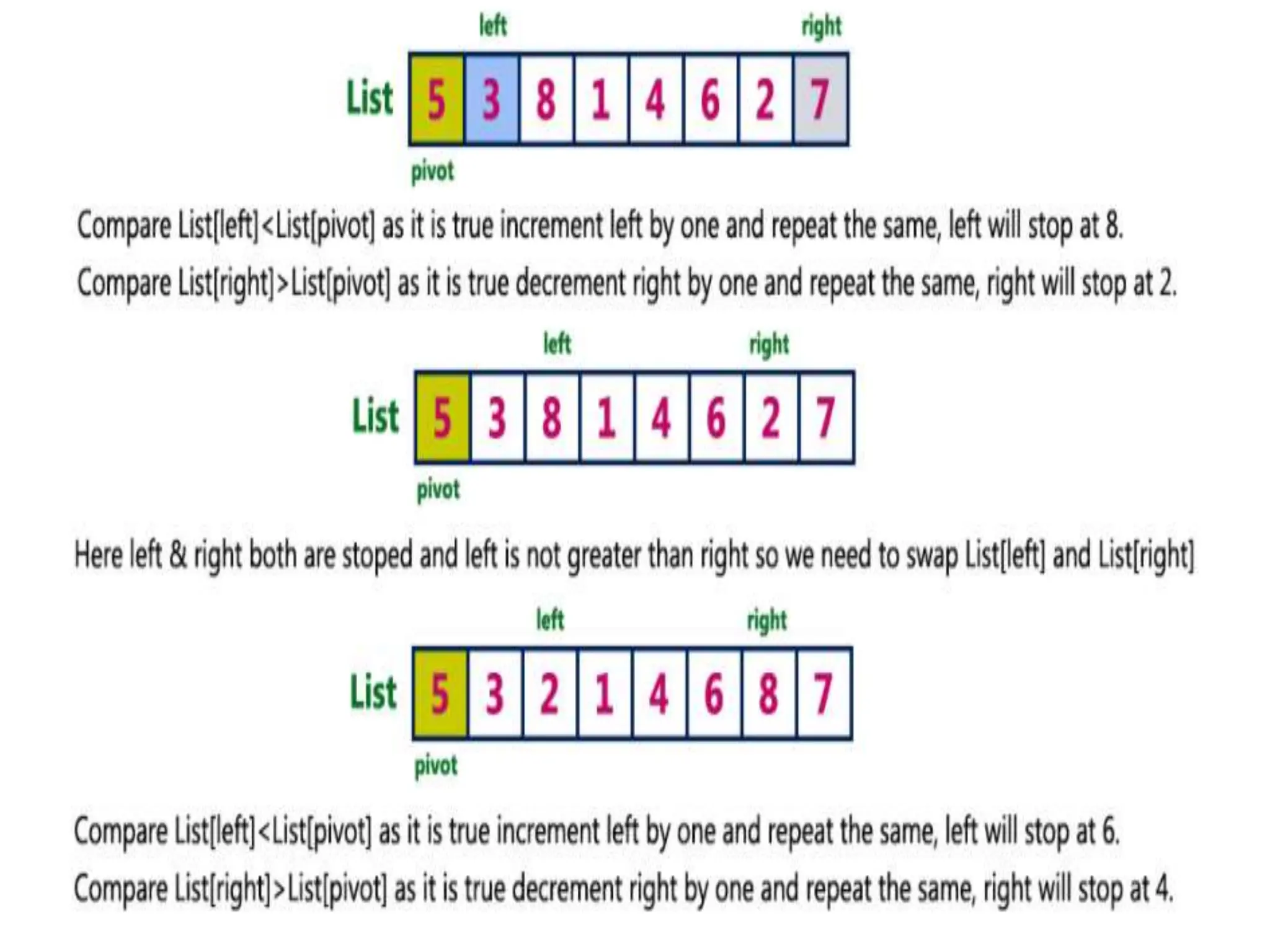
43. Quick Sort Algorithm
quickSort(array, leftmostIndex, rightmostIndex)
if (leftmostIndex < rightmostIndex)
pivotIndex <- partition(array,leftmostIndex, rightmostIndex)
quickSort(array, leftmostIndex, pivotIndex - 1)
quickSort(array, pivotIndex, rightmostIndex)
partition(array, leftmostIndex, rightmostIndex)
set rightmostIndex as pivotIndex
storeIndex <- leftmostIndex - 1
for i <- leftmostIndex + 1 to rightmostIndex
if element[i] < pivotElement
swap element[i] and element[storeIndex]
storeIndex++
swap pivotElement and element[storeIndex+1]
return storeIndex + 1

44. Time Complexity
Best O(n*log n)
Worst O(n2)
Average O(n*log n)
Space Complexity O(log n)

45. Radix sort
• Radix sort is one of the sorting algorithms used to sort
a list of integer numbers in order.
• In radix sort algorithm, a list of integer numbers will be
sorted based on the digits of individual numbers.
• Sorting is performed from least significant digit to the
most significant digit.
• Radix sort algorithm requires the number of passes
which are equal to the number of digits present in the
largest number among the list of numbers.
• For example, if the largest number is a 3 digit number
then that list is sorted with 3 passes.

46. Step by Step Process
The Radix sort algorithm is performed using the following
steps...
Step 1 - Define 10 queues each representing a bucket for each
digit from 0 to 9.
Step 2 - Consider the least significant digit of each number in
the list which is to be sorted.
Step 3 - Insert each number into their respective queue based
on the least significant digit.
Step 4 - Group all the numbers from queue 0 to queue 9 in the
order they have inserted into their respective queues.
Step 5 - Repeat from step 3 based on the next least significant
digit.
Step 6 - Repeat from step 2 until all the numbers are grouped
based on the most significant digit.

51. Shell Sort
• A highly efficient sorting algorithm based on the
insertion sort algorithm is known as Shell Sort. The
large shifts as that of insertion sort are avoided, if in
case, the smaller value is far right and which has to be
moved to far left.
• The insertion sort is used on wide spread elements, to
sort them and then sort the less widely spaced
elements. The spacing is known as interval. This
interval is calculated based on Knuth’s formula as –
h = h * 3 + 1
where −
h is interval with initial value 1

52. Interval of 4 positions is taken.
The values are {35, 14}, {33, 19}, {42, 27} and
{10, 44}

53. • The values in each sub-list are compared and
swapped them (if necessary) in the original
array. After this step, the new array appears as
−

54. • Then, the interval of 1 is taken and this gap
generates two sub-lists - {14, 27, 35, 42}, {19,
10, 33, 44}

55. • The values are compared and swapped, if
required, in the original array. After this step,
the array appears as −
• Finally, the rest of the array is sorted using
interval of value 1. Shell sort uses insertion
sort to sort the array.