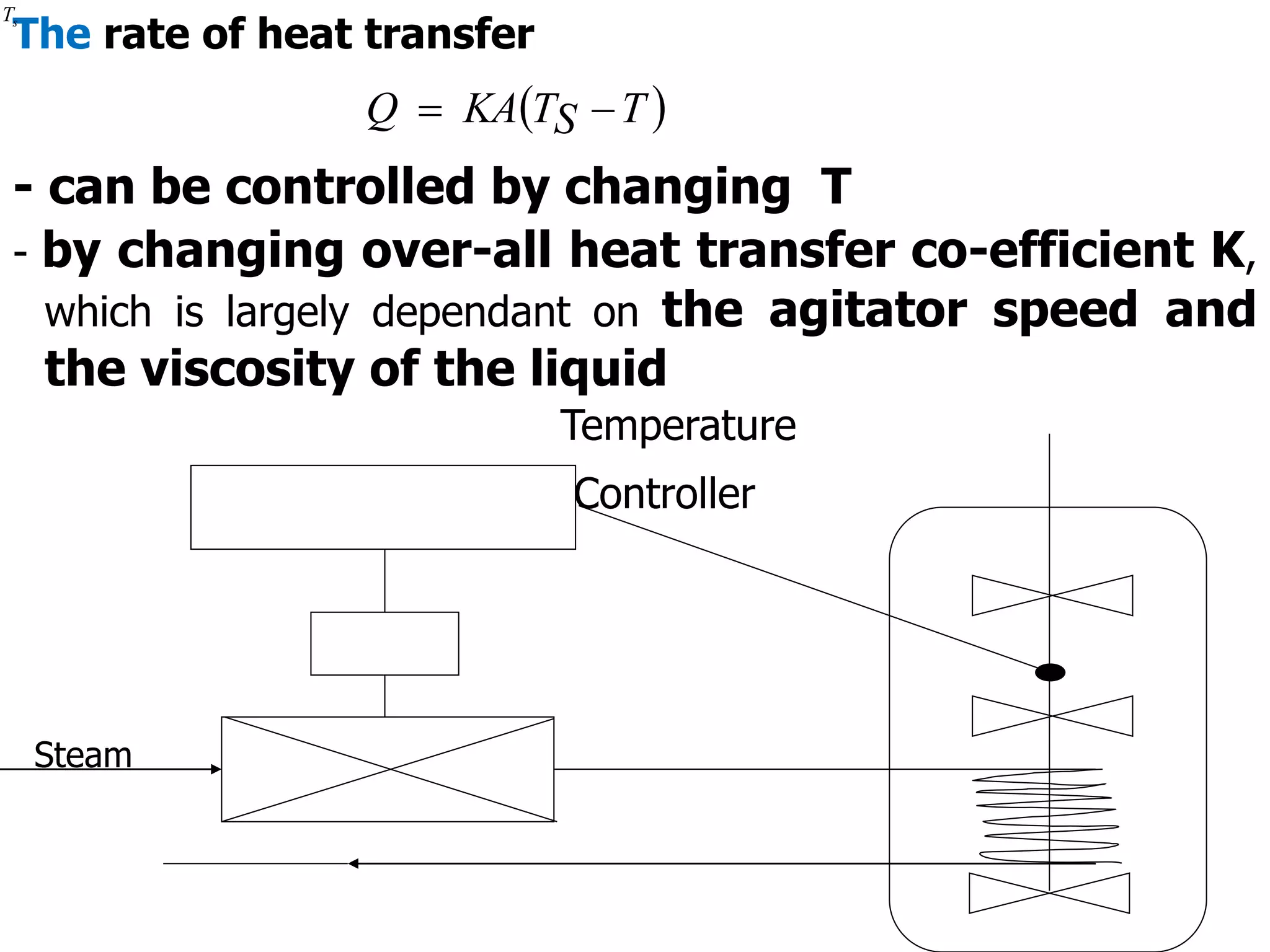
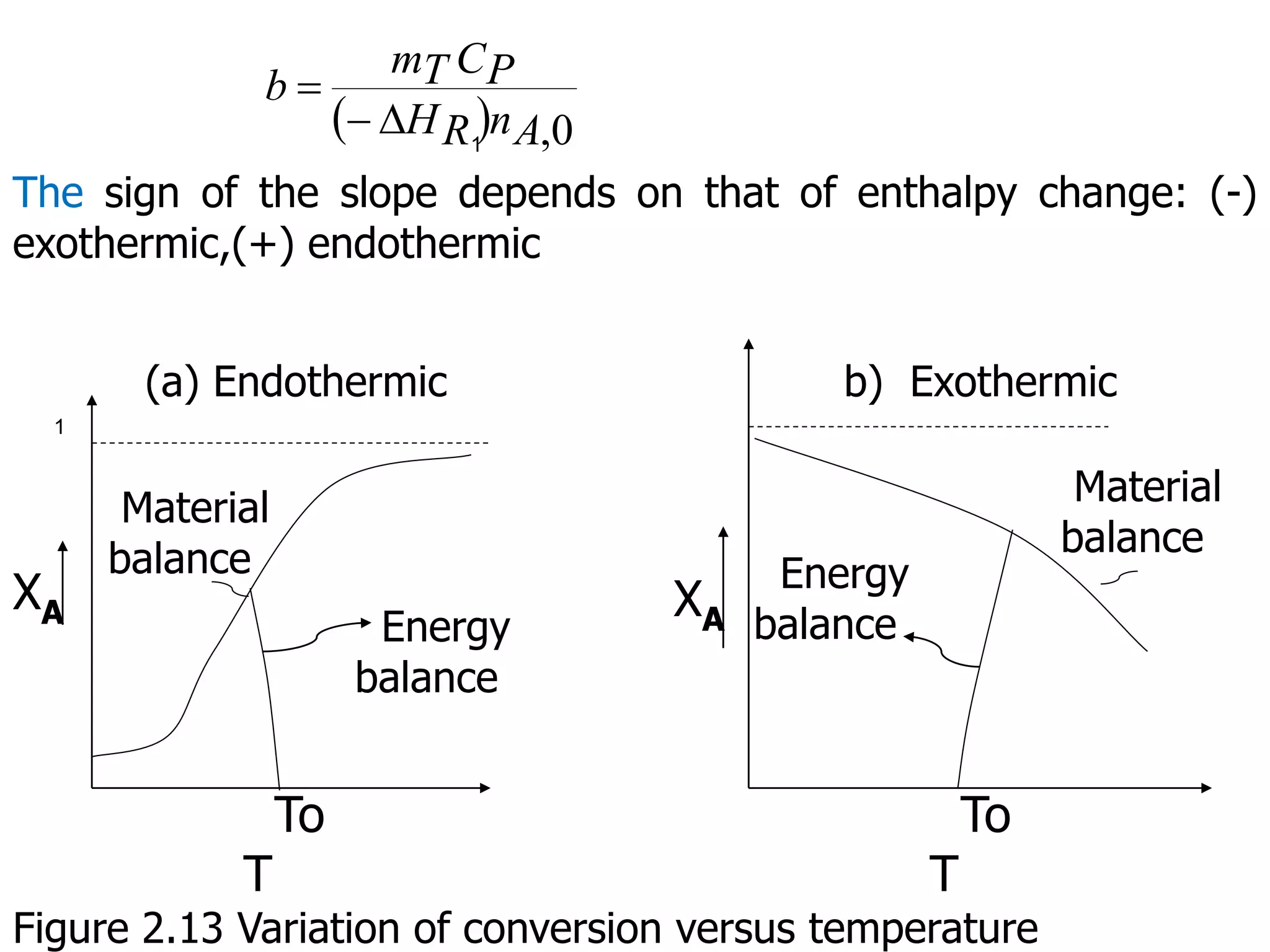
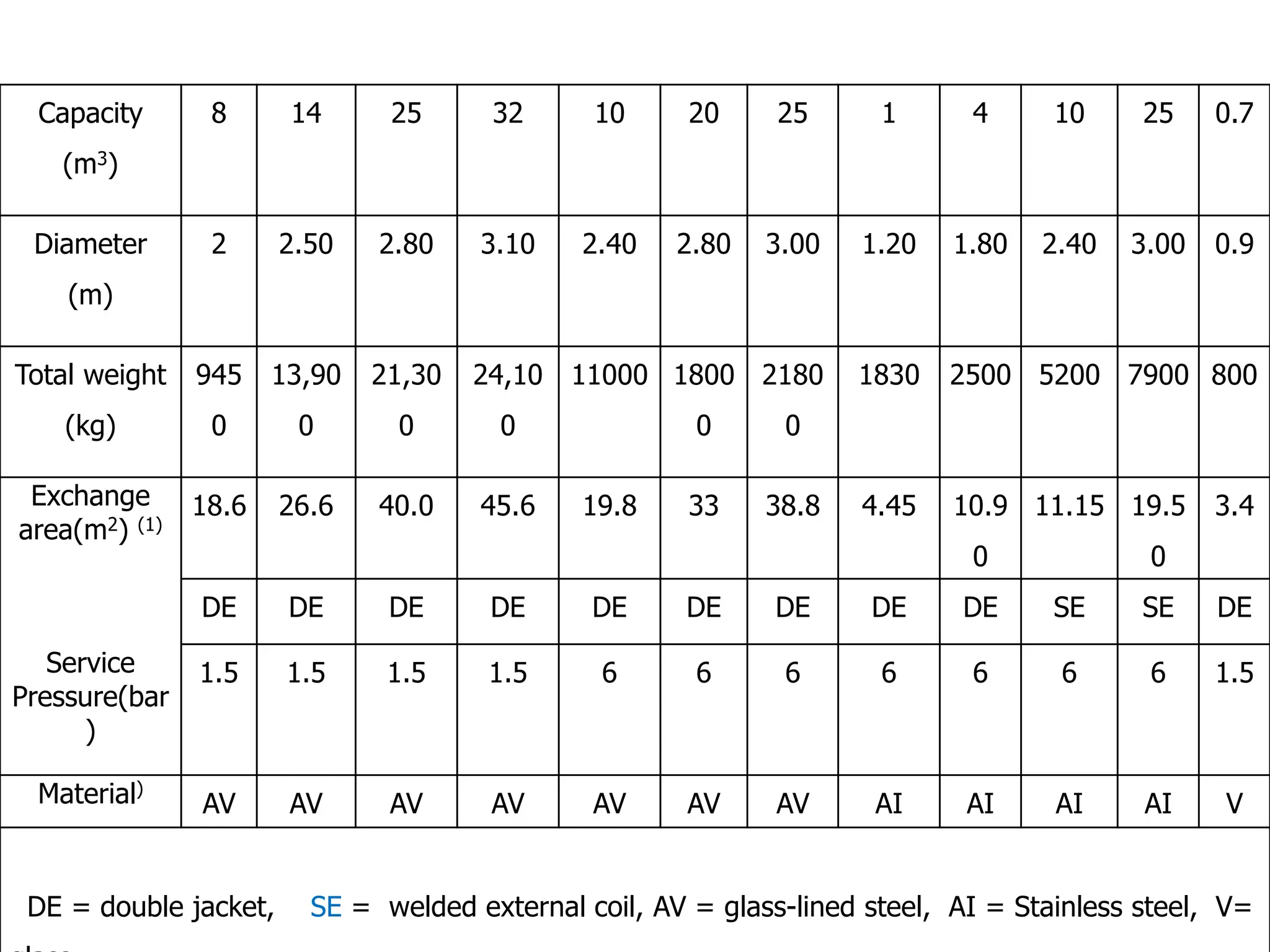
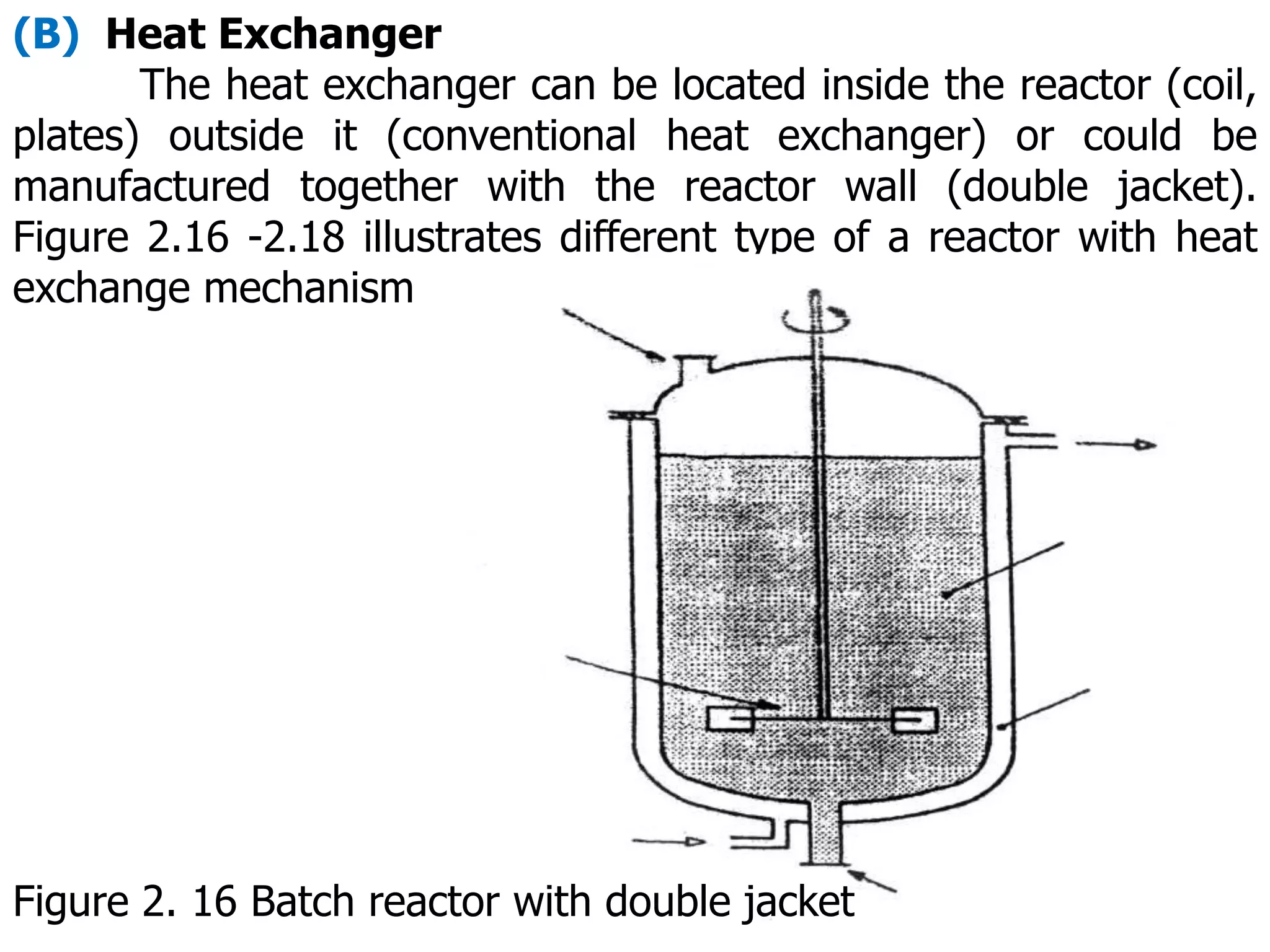
This document discusses the design of batch and semi-batch reactors. It describes the key characteristics of ideal batch reactors, including that no material enters or leaves during the reaction, the composition is a function of time only, and the concentration and temperature are uniform throughout the reactor volume. It provides equations for calculating reaction time based on conversion for batch reactor design. It also discusses considerations for non-isothermal reactors, including how temperature changes can affect the rate constant and integration of design equations. Heat effects on batch reactors are examined, including approaches for isothermal and non-isothermal operation.