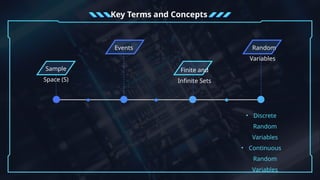
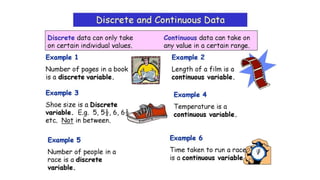
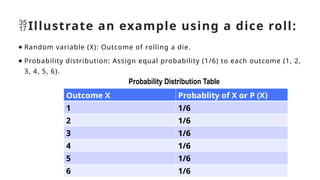
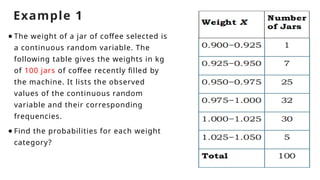
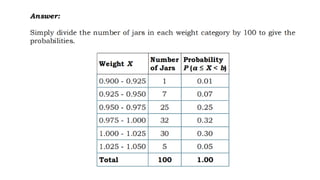
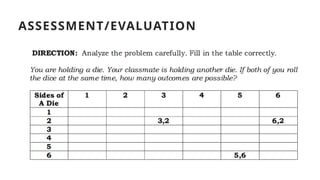
The document discusses the concept of random variables, differentiating between discrete and continuous types while providing real-life examples. It outlines objectives for understanding sample spaces, events, and probability distributions, alongside guided activities to classify and predict outcomes related to random variables. Additionally, it includes an assessment assignment focused on applying these concepts to real-life situations.

1. Statistics and
Probability
Random Variables
Sir Julius
YOUR LOGO
SCIENCE

2. 01
Define a random
variable.
OBJECTIVES
02
Differentiate between
discrete and
continuous random
variables
03
Illustrate examples
of random variables
from real-life
scenarios.
04
Identify random
variables as
either discrete or
continuous.
05
Understand the
terms: sample space
(S), events, finite
sets, and infinite
sets.
06
Topic

3. ACTIVITY 1
01ADD A SHORT DESCRIPTION

4. ●Toss a coin three times. Ask students to predict the
outcomes and discuss the possible results (e.g., 2 heads
and 1 tail). Write their responses on the board.
How can we assign a number to these
outcomes?

5. Key Terms and Concepts
Random
Variables
• Discrete
Random
Variables
• Continuous
Random
Variables
Sample
Space (S)
Events
Finite and
Infinite Sets

6. Examples:
• For a coin toss, S = {H, T}.
• For rolling a die, S = {1, 2, 3, 4, 5, 6}.
Sample Space (S)

7. EVENTS
●Events in probability can be defined as certain outcomes of a
random experiment. Events in probability are a subset of the
sample space. The types of events in probability are simple, sure,
impossible, complementary, mutually exclusive, exhaustive,
equally likely, compound, independent, and dependent events.
Example: Rolling an even number on a die is
an event E = {2, 4, 6}.

8. Finite and Infinite
Sets

9. Finite and Infinite
Sets

10. RANDOM
VARIABLES
02ADD A SHORT DESCRIPTION

11. RANDOM
VARIABLES
02ADD A SHORT DESCRIPTION
A random variable is a function that assigns a numerical value to
each outcome in a sample space.

12. RANDOM
VARIABLES
02ADD A SHORT DESCRIPTION
Examples:
Tossing a coin three times – Let X = number of heads.
Rolling a die – Let Y = the number rolled.
Measuring rainfall in a day – Let Z = amount of rainfall in millimeters.

13. Types of Random
Variables
Example: Number of goals scored in a soccer match.
Example: Weight of a student in kilograms.

15. Guided Practice
● Activity: Classify the following as discrete or continuous random variables, and
identify the sample space (S):
● Number of cars passing through a checkpoint in an hour.
● Time taken to complete a test.
● Temperature recorded at noon.
● Number of students in a classroom.

18. Rev iew: Re c a p t he prev ious le ss on o n ba s ic proba bilit y c o nc e pt s
a nd c onnec t it t o t he da y ’s t o pic .

19. I. OBJ E CT IVE S
●At the end of the lesson, students should be able to:
●1.Define and differentiate random variables and probability
distributions.
●2.Illustrate a probability distribution for a discrete random
variable.
●3.Identify the properties of a probability distribution for a
discrete random variable.
●4.Apply the concepts to real-life problems, such as decision-
making and games of chance.

20. Activity 1:
● Play a quick guessing game where students predict outcomes of rolling a die.
● Example: "If we roll a die, what are the possible outcomes? Can we assign
probabilities to these outcomes?"
● Possible outcomes when rolling a die: {1, 2, 3, 4, 5, 6}. Each outcome has a
probability of 1/6.
● "The outcomes of rolling a die are an example of random variables, which we’ll
explore today."

21.  A variable whose
possible values are
numerical outcomes of a
random phenomenon.

24. Probability Distribution for Discrete Random Variables
●A statistical distribution that can be represented by table,
graph, or formula that assigns probabilities to each
possible value of a random variable.

25. Illustrate an example using a dice roll:
● Random variable (X): Outcome of rolling a die.
● Probability distribution: Assign equal probability (1/6) to each outcome (1, 2,
3, 4, 5, 6).
Probability Distribution Table
Outcome X Probablity of X or P (X)
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
6 1/6

27. Application to Real-Life Problems
PROBABILITIES AS RELATIVE FREQUENCY
●In an experiment or survey, relative frequency of an event is the
number of times the event occurs divided by the total number of
trials. For instance, if you observed 100 passing cars and found
that 23 of them were red, the relative frequency would be
23/100.

28. Example 1
● The weight of a jar of coffee selected is
a continuous random variable. The
following table gives the weights in kg
of 100 jars of coffee recently filled by
the machine. It lists the observed
values of the continuous random
variable and their corresponding
frequencies.
● Find the probabilities for each weight
category?

30. EXPECTED VALUE OF A RANDOM VARIABLE

32. Let Us Remember (Generalization)

34. ASSESSMENT/EVALUATION

35. ASSIGNMENT
●Research a real-life problem that involves a random variable
(e.g., lottery, weather prediction). Identify the random variable
and construct a probability distribution table. Prepare to present
your findings in the next class. (20 Points)