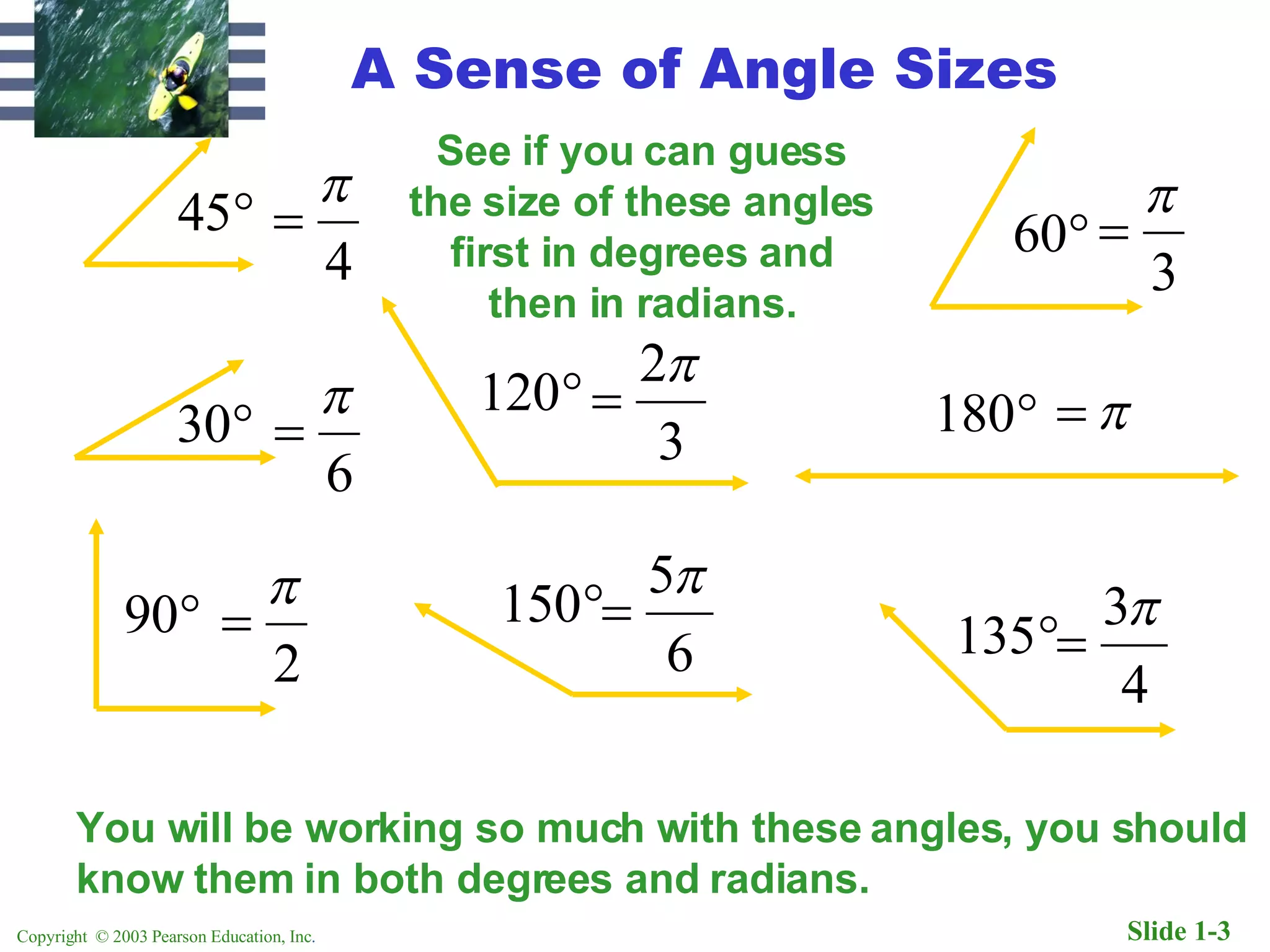
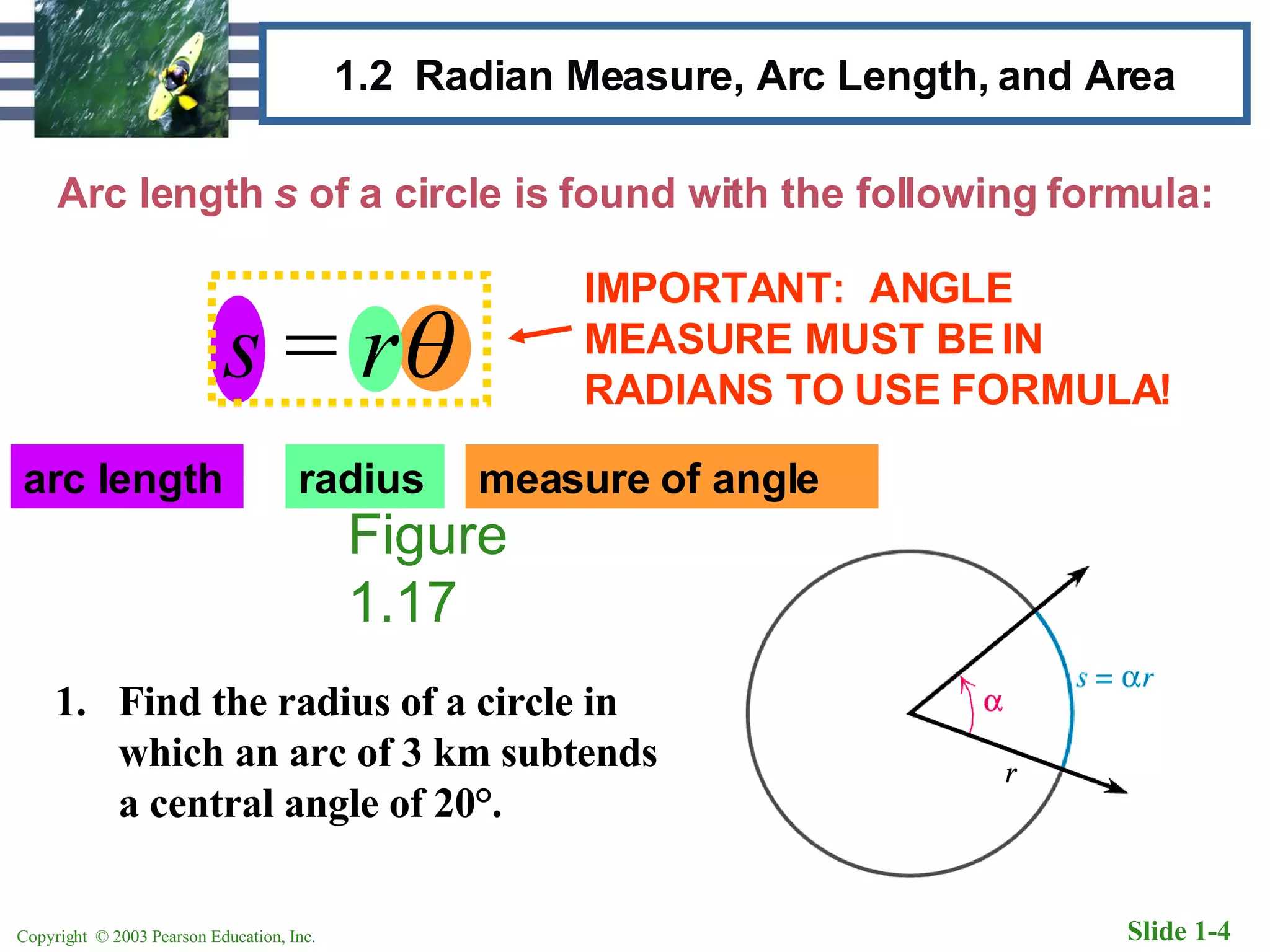
1. Radian measure relates the angle measure to the arc length intercepted by the angle on a circle of radius r. If the arc length is equal to r, the angle measure is 1 radian. 2. To use formulas for arc length and area of a sector, the angle measure must be in radians. The document provides conversions between degrees and radians and examples of using the arc length and area formulas. 3. The key ideas are that radian measure relates the angle to arc length on a circle, and formulas require the angle be in radians rather than degrees. Examples show converting between degrees and radians and using the formulas.

1. 1.2 Radian Measure, Arc Length, and Area Another way to measure angles is using what is called radians . Given a circle of radius r with the vertex of an angle as the center of the circle, if the arc length formed by intercepting the circle with the sides of the angle is the same length as the radius r , the angle measures one radian. initial side terminal side radius of circle is r r r arc length is also r r This angle measures 1 radian

2. 1.2 Radian Measure, Arc Length, and Area 180 º =  radians We need a conversion from degrees to radians. We could use a conversion fraction if we knew how many degrees equaled how many radians. 1. Change to degrees a. 4  /3 b.  /8 Change to radians a. -135 º b. 54º 3. Express  = 4 in terms of degrees, minutes, seconds (Change 4 radians to degrees, minutes, and seconds.) Convertion: degrees radians

3. A Sense of Angle Sizes See if you can guess the size of these angles first in degrees and then in radians. You will be working so much with these angles, you should know them in both degrees and radians.

4. 1.2 Radian Measure, Arc Length, and Area Arc length s of a circle is found with the following formula: Figure 1.17 Find the radius of a circle in which an arc of 3 km subtends a central angle of 20 °. arc length radius measure of angle IMPORTANT: ANGLE MEASURE MUST BE IN RADIANS TO USE FORMULA! s = r 

5. 1.2 Radian Measure, Arc Length, and Area Find the arc length if we have a circle with a radius of 3 meters and central angle of 0.52 radian. If the measure of the angle is in degrees, we can't use the formula until we convert it to radians. 3  = 0.52 arc length to find is in black s = r  3 0.52 = 1.56 m

6. 1.2 Radian Measure, Arc Length, and Area Area of a Sector of a Circle Again  must be in RADIANS so if it is in degrees you must convert to radians to use the formula. The formula for the area of a sector of a circle (shown in red here) is derived in your textbook. It is:  r

7. Given an arc of length 4 ft and a circle of radius 7 ft, find the exact radian measure of the central angle subtended by the arc; then find the area of the sector determined by the central angle.