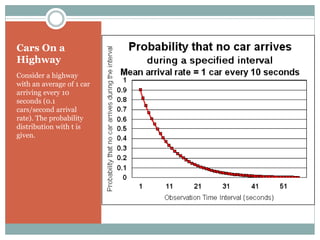
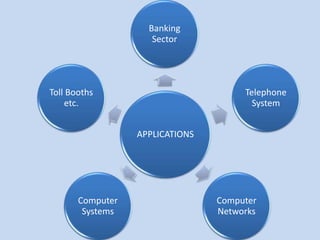
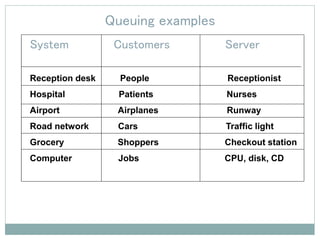
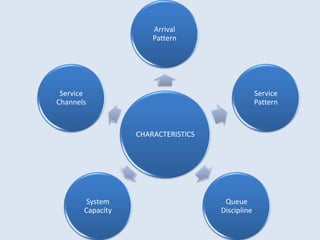
This presentation discusses queuing theory and the M/M/1 queuing model. It defines a queue as any system where jobs arrive looking for service and depart once served. Characteristics of queue systems include the arrival and service patterns, queue discipline, system capacity, and number of service channels. An example M/M/1 queuing simulation is presented using arrival and service times. The assumptions of the M/M/1 model are that the number of customers is large, the impact of each customer is small, and customers are independent with FIFO queue discipline and a single server. Applications of queuing theory include banking, telephone systems, computer networks, computer systems, and toll booths.

1. IT-319 SEMINAR PRESENTATION
By:
Rishita Jaggi
1140213
IT-3

2. What is QUEUE?
 Any system where jobs arrive looking for service and
depart once service is provided is described as a
queue.
 The Queuing theory provides predictions about
waiting times, the average number of waiting
customers, the length of a busy period and so forth.

3. Queue Representation

4. System Customers Server
Reception desk People Receptionist
Hospital Patients Nurses
Airport Airplanes Runway
Road network Cars Traffic light
Grocery Shoppers Checkout station
Computer Jobs CPU, disk, CD
Queuing examples

5. CHARACTERISTICS
Arrival
Pattern
Service
Pattern
Queue
Discipline
System
Capacity
Service
Channels

6. SIMULATION OF QUEUE

7. EXAMPLE:
AT=[0,10,15,35,30,10,5,5]
ST=[20,15,10,5,15,15,10,10]

8. M/M/1 QUEUING SYSTEM

9. Assumptions of M/M/1 Queuing System
 The number of customers in the system is very large.
 Impact of a single customer on the performance of
the system is very small.
 All customers are independent.
 A single server for the queue.
 The queue discipline for this system is FIFO.

10. Mathematical Modeling
Putting n=0
•t is used to define the interval 0 to t
•n is the total number of arrivals in the interval
0 to t.
•lambda is the total average arrival rate in
arrivals/sec.

11. Cars On a
Highway
Consider a highway
with an average of 1 car
arriving every 10
seconds (0.1
cars/second arrival
rate). The probability
distribution with t is
given.

12. M/M/1 Results
ρ = λ / µ
•rho is occupancy (traffic intensity)
•mu is average service rate.
•N is mean number of customers.
•T is total waiting time.

13. APPLICATIONS
Banking
Sector
Telephone
System
Computer
Networks
Computer
Systems
Toll Booths
etc.