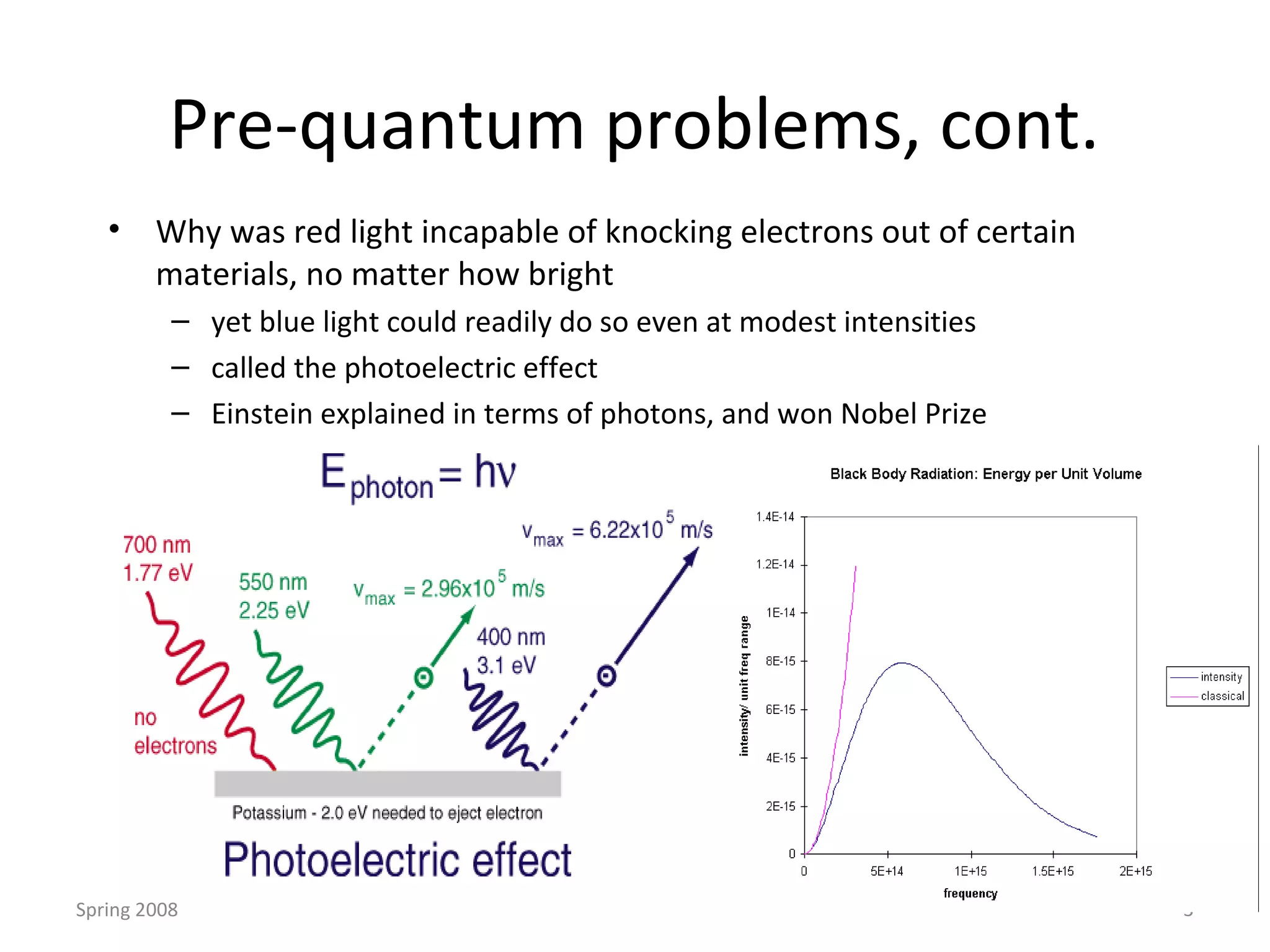
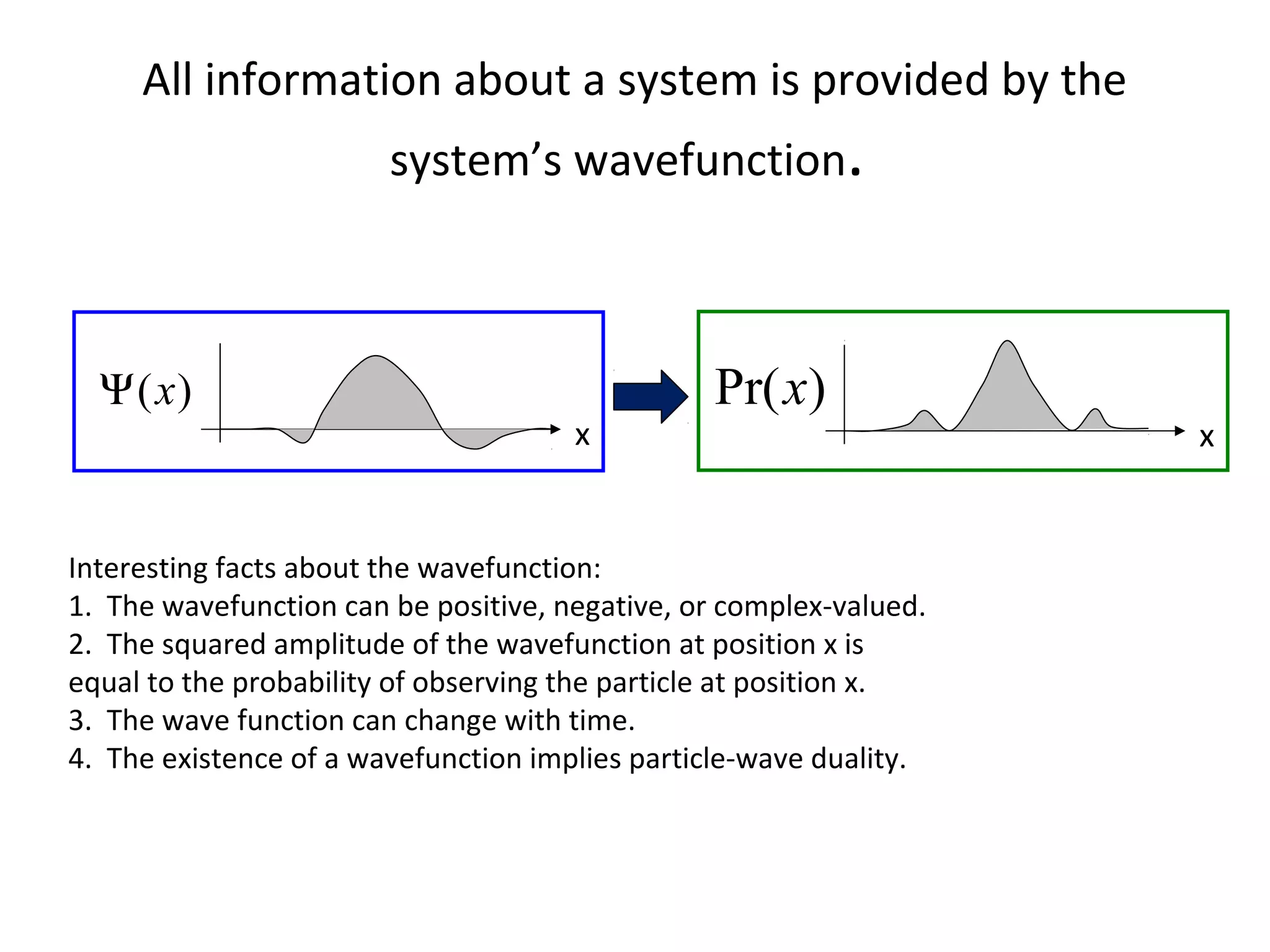
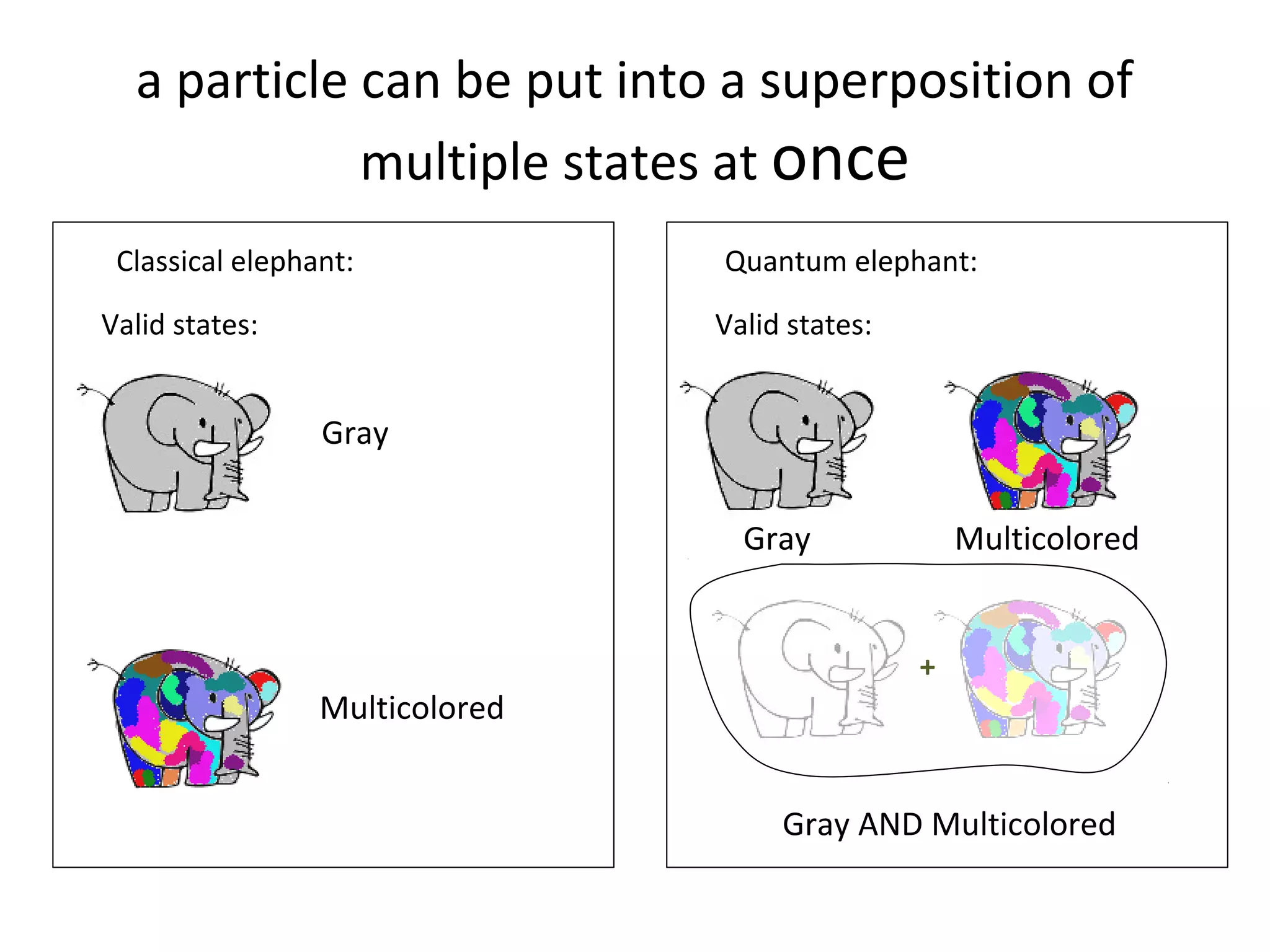
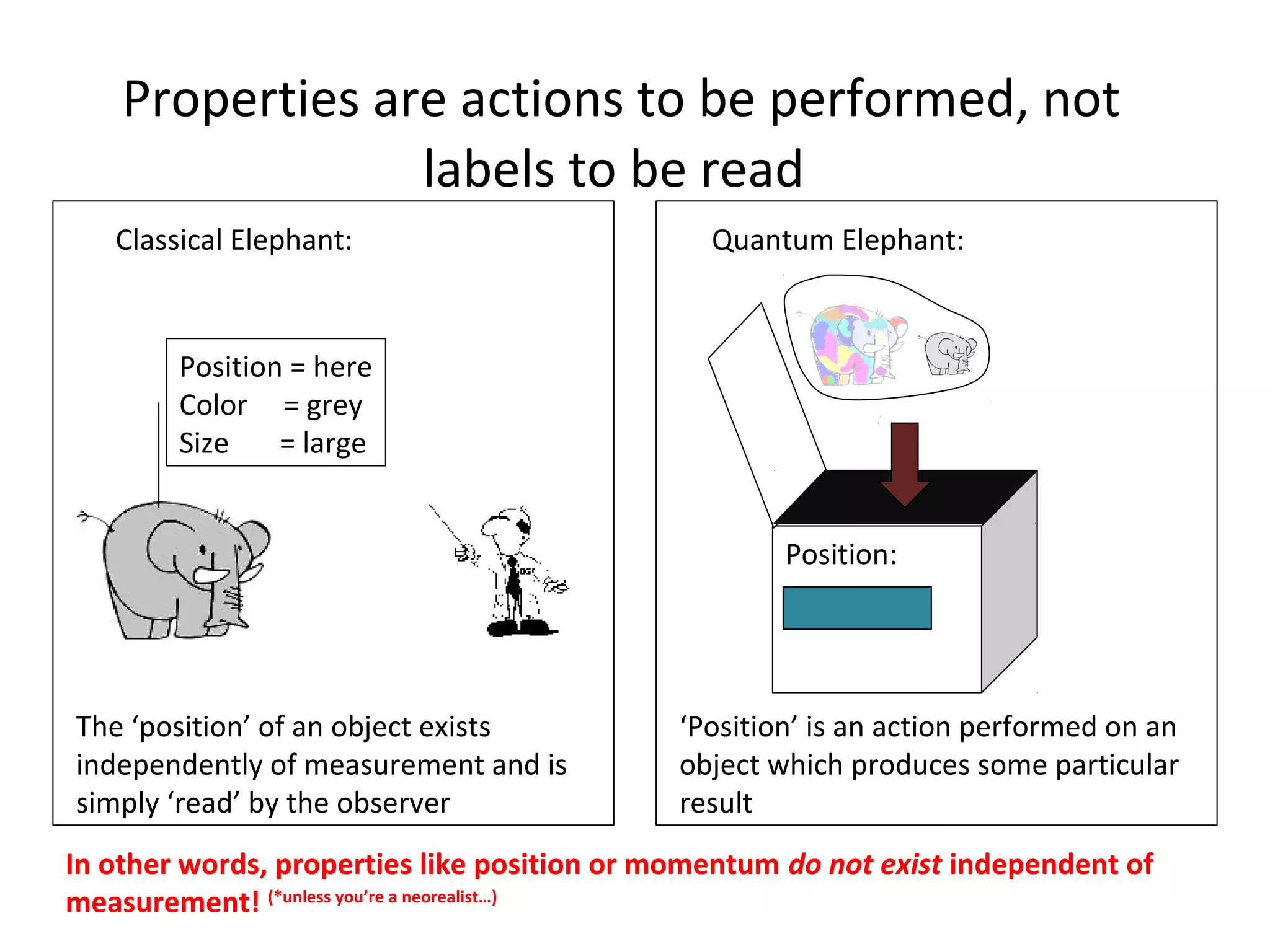
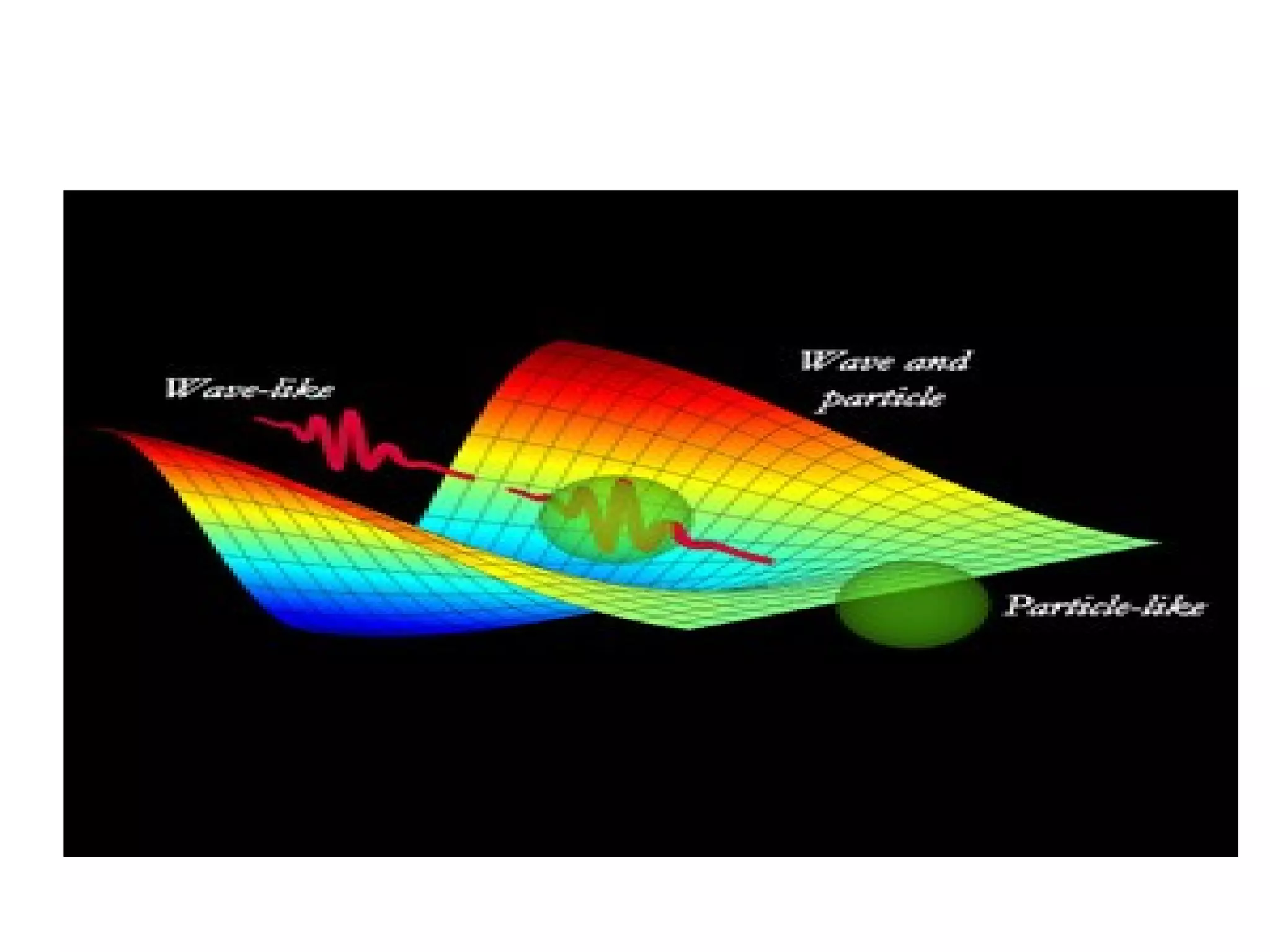
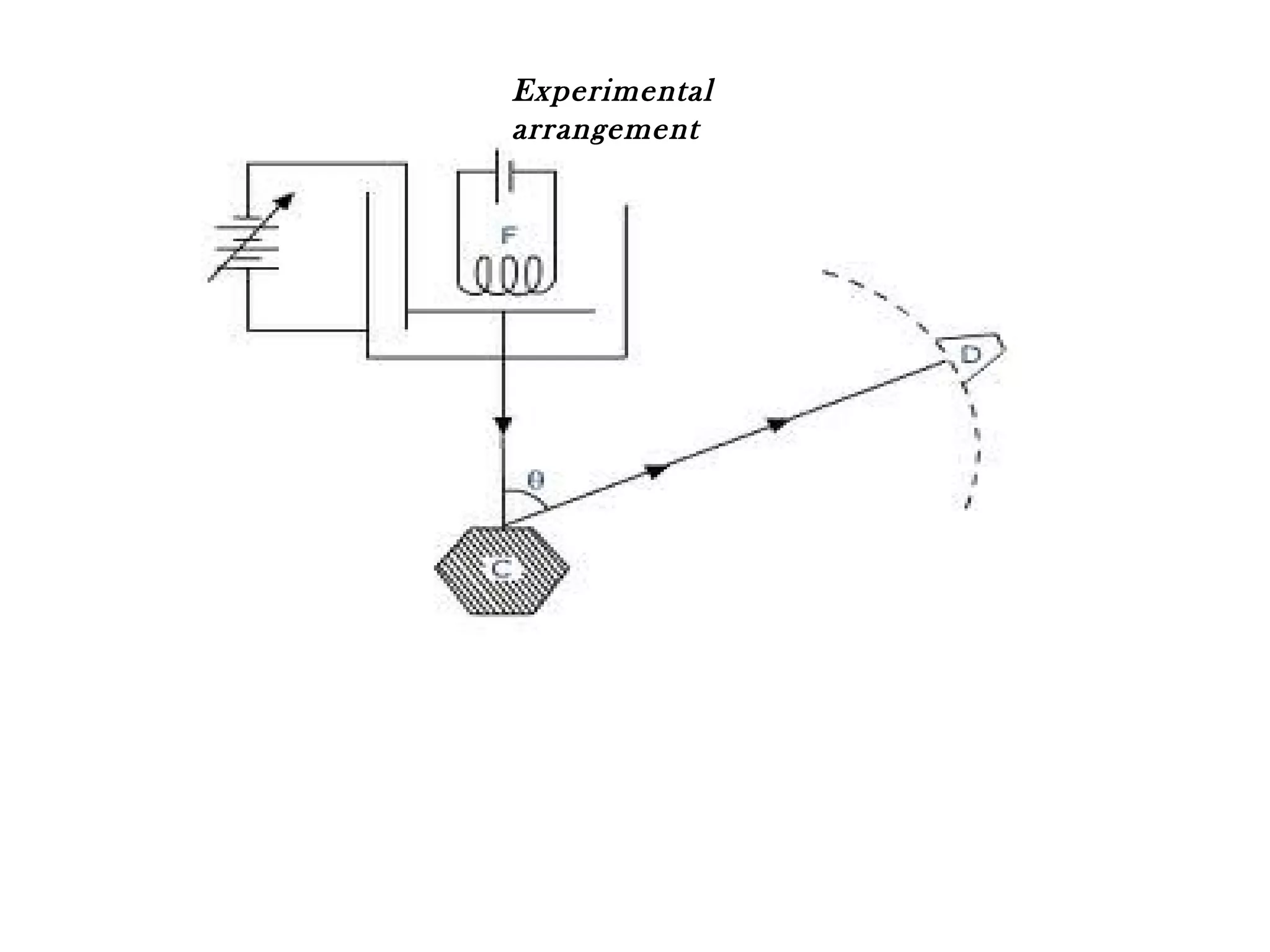
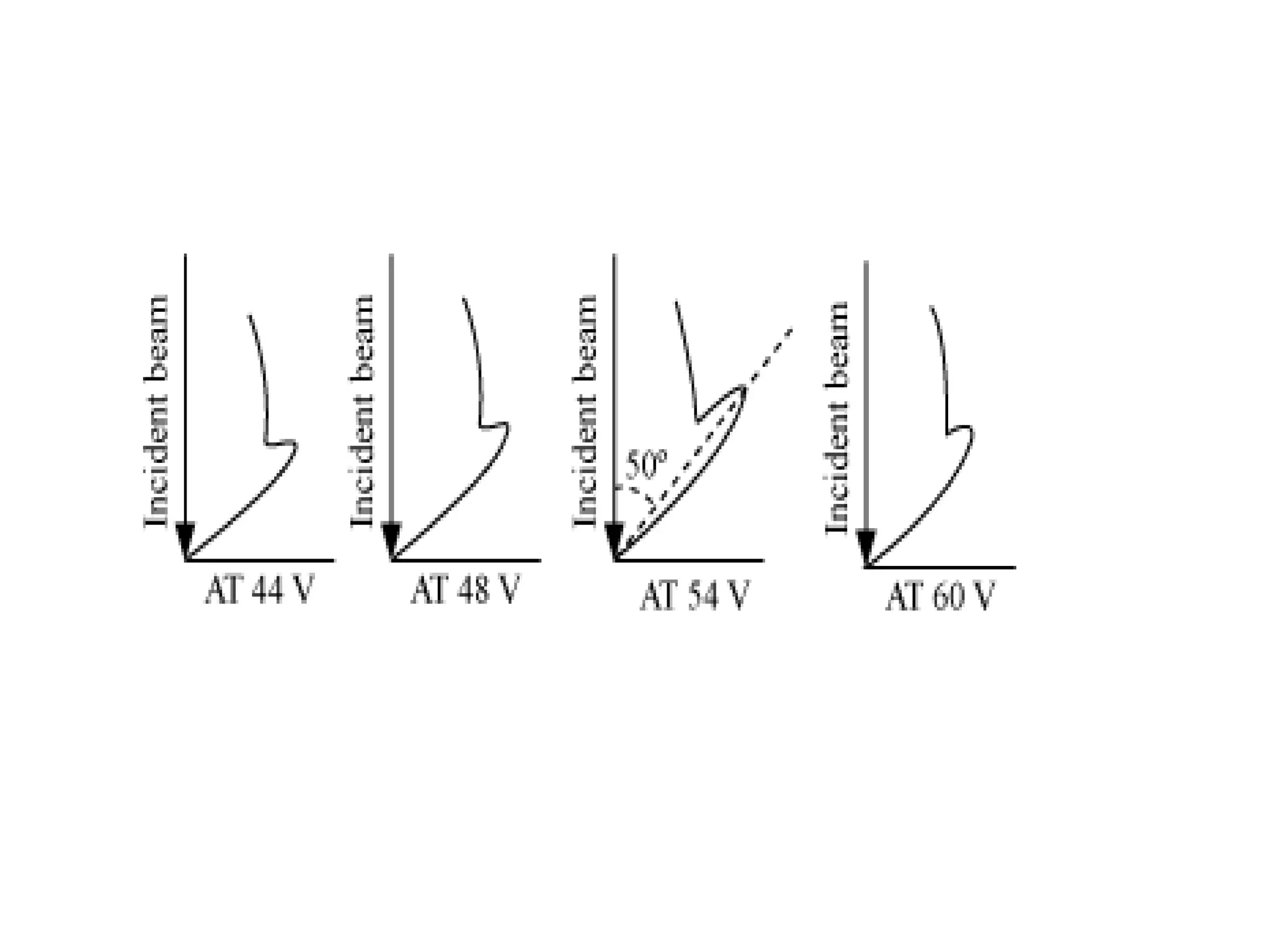
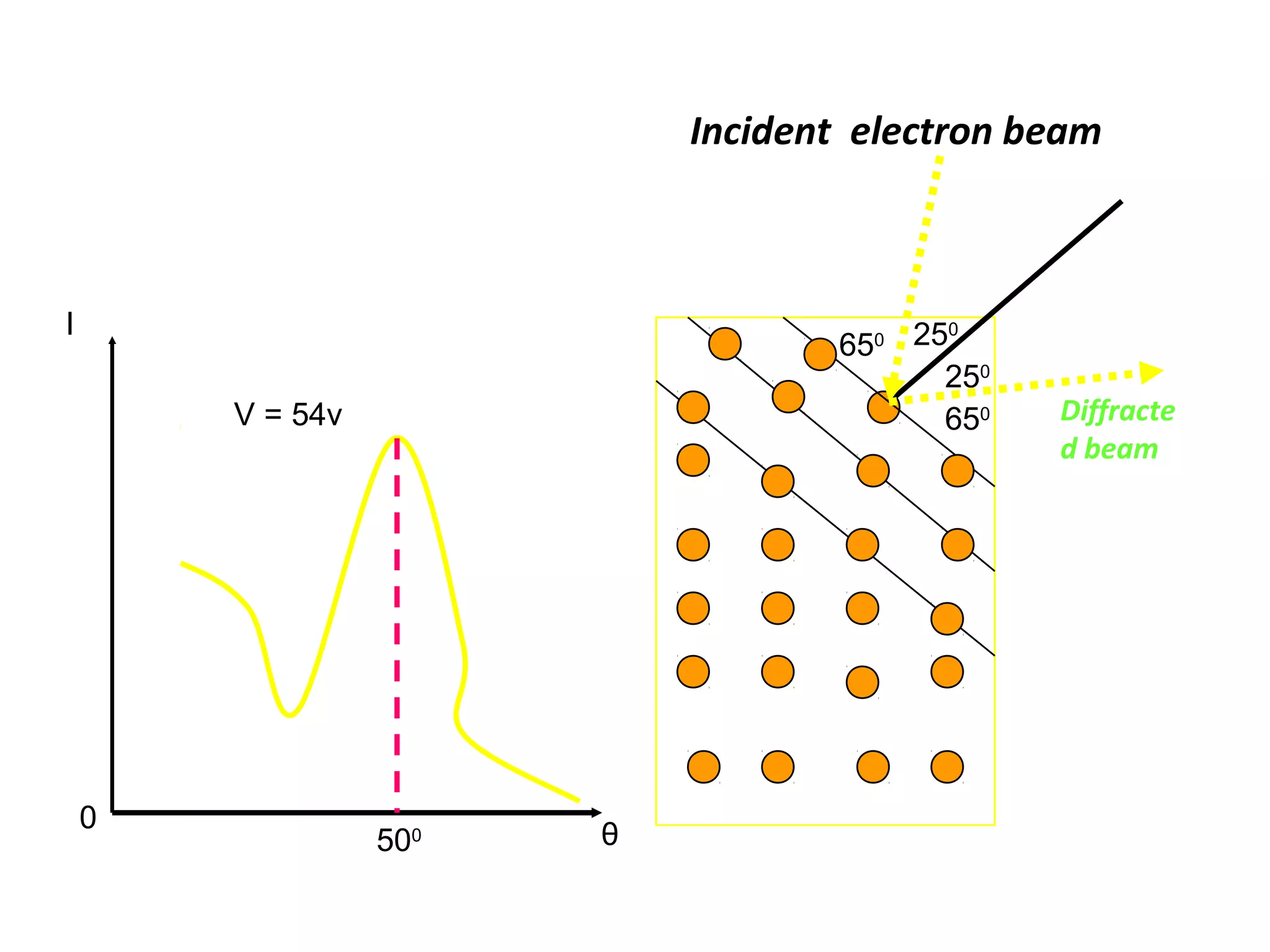
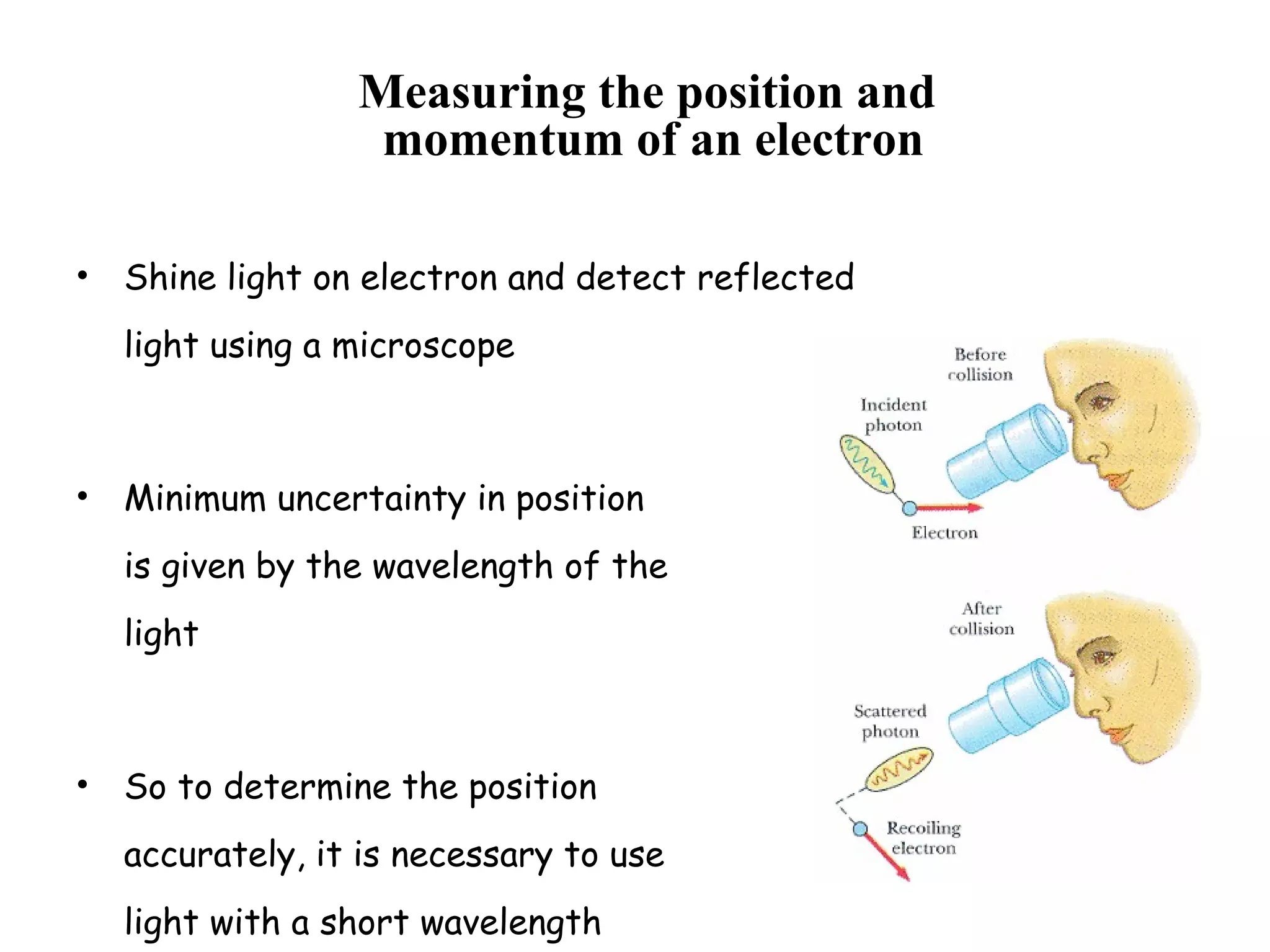
Quantum mechanics describes the behavior of matter and light on the atomic and subatomic scale. Some key points of the quantum mechanics view are that particles can exhibit both wave-like and particle-like properties, their behavior is probabilistic rather than definite, and some properties like position and momentum cannot be known simultaneously with complete precision due to the Heisenberg uncertainty principle. Quantum mechanics has successfully explained various phenomena that classical physics could not and led to important technologies like lasers, MRI machines, and semiconductor devices.

1. Quantum MechanicsQuantum Mechanics

2. 2
The Quantum Mechanics View
• All matter (particles) has wave-like properties
– so-called particle-wave duality
• Particle-waves are described in a probabilistic manner
– electron doesn’t whiz around the nucleus, it has a probability
distribution describing where it might be found
– allows for seemingly impossible “quantum tunneling”
• Some properties come in dual packages: can’t know both
simultaneously to arbitrary precision
– called the Heisenberg Uncertainty Principle
– not simply a matter of measurement precision
– position/momentum and energy/time are example pairs
• The act of “measurement” fundamentally alters the system
– called entanglement: information exchange alters a particle’s state

3. Spring 2008 3
Pre-quantum problems, cont.
• Why was red light incapable of knocking electrons out of certain
materials, no matter how bright
– yet blue light could readily do so even at modest intensities
– called the photoelectric effect
– Einstein explained in terms of photons, and won Nobel Prize

4. 4
• Without Quantum Mechanics, we could never have designed
and built:
– semiconductor devices
• computers, cell phones, etc.
– lasers
• CD/DVD players, bar-code scanners, surgical applications
– MRI (magnetic resonance imaging) technology
– nuclear reactors
– atomic clocks (e.g., GPS navigation)
• Physicists didn’t embrace quantum mechanics because it was
gnarly, novel, or weird
– it’s simply that the #$!&@ thing worked so well

5. 5
The Double Slit Experiment
particle? wave?

6. 6
Results
• The pattern on the screen is an interference
pattern characteristic of waves
• So light is a wave, not particulate
• But repeat the experiment one photon at a time
• Over time, the photons only land on the
interference peaks, not in the troughs
– consider the fact that they also pile up in the middle!
– pure ballistic particles would land in one of two spots

7. Classical mechanics is the mechanics
of everyday objects like tables and
chairs
Sir Isaac Newton
1. An object in motion tends to stay in motion.
2. Force equals mass times acceleration
3. For every action there is an equal and
opposite reaction.

8. Classical mechanics reigned as the dominant theory of
mechanics for centuries
1687 – Newton’s Philosophiae
Mathematica
1788 – Lagrange’s Mecanique
Analytique
1834 – Hamiltonian mechanics
1864 – Maxwell’s equations
1900 – Boltzmann’s
entropy equation

9. However, several experiments at the beginning
of the 20th
-century defied explanation
The Ultraviolet
Catastrophe
The Hydrogen
Spectrum
The Stern-Gerlach
Experiment
Newtonian explanations for
these phenomena were wildly
insufficient
?

10. Classical Physics
• Described by Newton’s Law of Motion (17th
century)
– Successful for explaining the motions of
objects and planets
– In the end of 19th
century, experimental
evidences accumulated showing that classical
mechanics failed when applied to very small
particles.
),...,,(
2
21 N
i i
i
U
m
p
H rrr∑ +=
Sir Isaac Newton

11. The failures of Classical Physics
• Black-body radiation
– A hot object emits light (consider hot metals)
– At higher temperature, the radiation becomes shorter
wavelength (red  white  blue)
– Black body : an object capable of emitting and
absorbing all frequencies uniformly

12. The failures of classical physics
• Experimental observation
– As the temperature raised, the peak in the
energy output shifts to shorter
wavelengths.
– Wien displacement law
– Stefan-Boltzmann law
Wihelm Wien
2max
5
1
cT =λ Kcm44.12 =c
4
/ aTVE ==Ε 4
TM σ=

13. Rayleigh – Jeans law
• First attempted to describe energy
distribution
• Used classical mechanics and equi-
partition principle
• Although successful at high wavelength, it
fails badly at low wavelength.
• Ultraviolet Catastrophe
– Even cool object emits visible and UV
region
– We all should have been fried !
Lord Rayleigh
λρddE = 4
8
λ
π
ρ
kT
=

14. Planck’s Distribution
• Energies are limited to discrete value
– Quantization of energy
• Planck’s distribution
• At high frequencies approaches the Rayleigh-Jeans
law
• The Planck’s distribution also follows Stefan-
Boltzmann’s Las
Max Planck
,...2,1,0, == nnhE ν
λρddE =
)1(
8
/5
−
= kThc
e
hc
λ
λ
π
ρ
kT
hc
kT
hc
e kThc
λλ
λ
≈−++=− 1....)1()1( /

15. 15
Let’s start with photon energy
• Light is quantized into packets called photons
• Photons have associated:
– frequency, ν (nu)
– wavelength, λ (λν = c)
– speed, c (always)
– energy: E = hν
• higher frequency photons → higher energy → more
damaging
– momentum: p = hν/c
• The constant, h, is Planck’s constant
– has tiny value of: h = 6.63×10-34
J·s

16. Wave-Particle Duality
-The particle character of wave
• Particle character of electromagnetic radiation
– Observation :
• Energies of electromagnetic radiation of frequency v
can only have E = 0, h, v 2hv, …
(corresponds to particles n= 0, 1, 2, … with energy = hv)
– Particles of electromagnetic radiation : Photon
– Discrete spectra from atoms and molecules can be explained
as generating a photon of energy hn .
– ∆E = hv

17. Quantum mechanics was developed to explain these results and
developed into the most successful physical theory in history
1900 – Planck’s constant
1913 – Bohr’s model
of the atom
1925 – Pauli exclusion principle
1926 – Schrodinger equation
1948 – Feynmann’s path
integral formulation
Increasingweirdness
1954 – Everett’s many-world
theory

18. Although quantum mechanics applies to all objects, the effects of quantum
mechanics are most noticeable only for very small objects
How small is very small?
1 meter Looks classical
1 micrometer Looks classical
1 millimeter Looks classical
1 nanometer Looks quantum!

19. Nonetheless, quantum mechanics is
still very important.How important is very important?
Without quantum mechanics:
All atoms would be unstable.
Universe
explodes
Chemical bonding would be
impossible.
All molecules
disintegrate
Many biological reactions
would not occur.
Life does
not exist
Neil Shenvi’s dissertation title:
Vanity of Vanities, All is Vanity
Minimal
consequences

20. When you start going subatomic or even smaller, things get
strange. That strangeness, however, can lead to some pretty cool
inventions.

21. All information about a system is provided by the
system’s wavefunction.
( )xΨ
x
Pr( )x
x
Interesting facts about the wavefunction:
1. The wavefunction can be positive, negative, or complex-valued.
2. The squared amplitude of the wavefunction at position x is
equal to the probability of observing the particle at position x.
3. The wave function can change with time.
4. The existence of a wavefunction implies particle-wave duality.

22. At a given instant in time, the position and momentum of a
particle cannot both be known with absolute certainty
This consequence is known as Heisenberg’s uncertainty principle
Classical particle Quantum particle
Wavefunction = ψ(x)
Hello, my name is:
Classical particle
my position is 11.2392…Ang
my momentum is -23.1322… m/s
“I can tell you my exact position, but then I
can’t tell you my momentum. I can tell
you my exact momentum, but then I can’t
tell you my position. I can give you a
pretty good estimate of my position, but
then I have to give you a bad estimate of
my momentum. I can…”
?
??
?

23. a particle can be put into a superposition of
multiple states at once
Classical elephant:
Valid states:
Quantum elephant:
Gray
Multicolored
Gray Multicolored
Valid states:
+
Gray AND Multicolored

24. Properties are actions to be performed, not
labels to be read
Classical Elephant: Quantum Elephant:
The ‘position’ of an object exists
independently of measurement and is
simply ‘read’ by the observer
Position = here
Color = grey
Size = large
‘Position’ is an action performed on an
object which produces some particular
result
Position:
In other words, properties like position or momentum do not exist independent of
measurement! (*unless you’re a neorealist…)

25. WAVES
A wave is nothing but disturbance which is occurred
in a medium and it is specified by its frequency,
wavelength, phase, amplitude and intensity.
PARTICLES
A particle or matter has mass and it is located at a
some definite point and it is specified by its mass,
velocity, momentum and energy.

27. • The physical values or motion of a macroscopic
particles can be observed directly. Classical
mechanics can be applied to explain that motion.
• But when we consider the motion of Microscopic
particles such as electrons, protons……etc.,
classical mechanics fails to explain that motion.
• Quantum mechanics deals with motion of
microscopic particles or quantum particles.

28. de Broglie hypothesis
• In 1924 the scientist named de Broglie
introduced electromagnetic waves behaves
like particles, and the particles like
electrons behave like waves called matter
waves.
• He derived an expression for the
wavelength of matter waves on the analogy
of radiation.

29. • According to Planck’s radiation law
• Where ‘c’ is a velocity of light and ‘λ‘is a wave
length.
• According to Einstein mass-energy relation
From 1 & 2
)1..(..........
λ
ϑ
c
h
hE
=
=
p
h
mc
h
c
hmc
=
=
=
λ
λ
λ
2
)2......(2
mcE =

30. de Broglie wavelength associated with
electrons
Let us consider the case of an electron of rest
mass m0 and charge ‘ e ‘ being accelerated by a
potential V volts.
If ‘v ‘ is the velocity attained by the electron due
to acceleration
The de Broglie wavelength 0
2
0
2
2
1
m
eV
v
eVvm
=
=
A
V
m
eV
m
h
vm
h
0
0
0
0
26.12
2
=
=⇒=
λ
λλ

31. Characteristics of Matter waves
• Lighter the particle, greater is the wavelength
associated with it.
• Lesser the velocity of the particle, longer the
wavelength associated with it.
• For V= 0, λ=∞ . This means that only with moving
particle matter wave is associated.
• Whether the particle is charged or not, matter
wave is associated with it. This reveals that these
waves are not electromagnetic but a new kind of
waves .

32. It can be proved that the matter waves travel faster than light.
We know that
The wave velocity (ω) is given by
As the particle velocity v cannot
exceed velocity of light c,
ω is greater than velocity of light.
h
mc
mch
mcE
hE
2
2
2
=→=
=
=
ϑϑ
ϑ
v
c
w
mv
h
h
mc
where
mv
h
h
mc
w
w
2
2
2
&
))((
=
==
=
=
λϑ
ϑλ

33. Experimental evidence for matter waves
1.Davisson and Germer ’s Experiment.

34. DAVISSON & GERMER’S EXPERMENT
• Davison and Germer first detected electron waves
in 1927.
• They have also measured de Broglie wave lengths
of slow electrons by using diffraction methods.
Principle:
• Based on the concept of wave nature of matter fast
moving electrons behave like waves. Hence
accelerated electron beam can be used for
diffraction studies in crystals.

35. Experimental
arrangement

36. Experimental arrangement
• The electron gun G produces a fine beam of
electrons.
• It consists of a heated filament F, which emits
electrons due to thermo ionic emission
• The accelerated electron beam of electrons are
incident on a nickel plate, called target T. The target
crystal can be rotated about an axis perpendicular to
the direction of incident electron beam.
• The distribution of electrons is measured by using a
detector called faraday cylinder c and which is
moving along a graduated
circular scale S.
• A sensitive galvanometer connected to the detector.

37. ResultsResults
• When an electron beam accelerated by 54 volts was
directed to strike the nickel crystal, a sharp maximum in
the electron distribution occurred at scattered angle of 500
with the incident beam.
• For that scattered beam of electrons the diffracted angle
becomes 650.
• For a nickel crystal the inter planer separation is
d = 0.091nm.

39. 250
250
650
Incident electron beam
Diffracte
d beam
650
I
θ
0
V = 54v
500

40. • According to Bragg’s law
• For a 54 volts , the de Broglie wave
length associated with the electron is
given by
• This is in excellent agreement with the
experimental value.
• The Davison - Germer experiment
provides a direct verification of de
Broglie hypothesis of the wave nature
of moving particle.
nm
nm
nd
165.0
165sin091.02
sin2
0
=
×=××
=
λ
λ
λθ
nm
A
A
V
166.0
54
26.12
26.12
0
0
=
=
=
λ
λ
λ

41. Heisenberg realised that
• In the world of very small particles, one cannot measure any
property of a particle without interacting with it in some way
• This introduces an unavoidable uncertainty into the result
• One can never measure all the
properties exactly
Werner Heisenberg (1901-1976)

42. Measuring the position and
momentum of an electron
• Shine light on electron and detect reflected
light using a microscope
• Minimum uncertainty in position
is given by the wavelength of the
light
• So to determine the position
accurately, it is necessary to use
light with a short wavelength

43. Measuring the position and momentum
of an electron (cont’d)
• By Planck’s law E = hc/λ, a photon with a short wavelength has a
large energy
• Thus, it would impart a large ‘kick’ to the electron
• But to determine its momentum accurately,
electron must only be given a small kick
• This means using light of long wavelength!

44. Fundamental Trade Off …
• Use light with short wavelength:
– accurate measurement of position but not momentum
• Use light with long wavelength
– accurate measurement of momentum but not position

45. Heisenberg’s Uncertainty Principle
The more accurately you know the position (i.e.,
the smaller ∆x is) , the less accurately you know the
momentum (i.e., the larger ∆p is); and vice versa

46. Heisenberg uncertainty principle
statement
• This principle states that the product of
uncertainties in determining the both position
and momentum of particle is approximately
equal to h / 4Π.
Where Δx is the uncertainty in measuring
positiondetermine the position and Δp is the
uncertainty in determining momentum.
• This relation shows that it is impossible to
π4
h
px ≥∆∆

47. • This relation is universal and holds for all canonically
conjugate physical quantities like
1. Angular momentum & angle
2. Time & energy
π
π
θ
4
4
h
Et
h
j
≥∆∆
≥∆∆
Consequences of uncertainty principle
• Explanation for absence of electrons in the nucleus
• Diffraction of electrons through single slit.
• Existence of protons and neutrons inside nucleus.
• Uncertainty in the frequency of light emitted by an
atom.
• Energy of an electron in an atom
• .

48. Physical significance of the wave function
• The wave function ‘Ψ’ has no direct physical
meaning. It is a complex quantity representing
the variation of a Matter wave.
• The wave function Ψ( r, t ) describes the position
of a particle with respect to time.
• It can be considered as ‘probability amplitude’
since it is used to find the location of the
particle.

49. ΨΨ*
or ‫׀‬Ψ ‫׀‬2
is theprobability density function.
ΨΨ*
dx dy dz gives the probability of finding the electron
in the region of space between x and x + dx, y and y + dy,
z and z + dz.
The above relation shows that’s a ‘normalization condition’
of particle.
1
1
2
-
-
*
=
=
∫
∫
∞+
∞
+∞
∞
dxdydz
dxdydz
ψ
ψψ

50. Schrödinger time independent wave
equation
• Schrödinger wave equation is a basic principle of a
fundamental Quantum mechanics.
• Consider a particle of mass ‘m’ ,moving with
velocity ‘v’ and wavelength ‘λ’. According to de
Broglie,
)1.(..........
mv
h
p
h
=
=
λ
λ
Dirac, Heisenberg, and Schrödinger (L to R) at
the Stockholm train station on their way to the
Nobel Prize ceremony, December 1933.

51. • According to classical physics, the displacement for a
moving wave along X-direction is given by
• Where ‘A’ is a amplitude ‘x’ is a position co-ordinate and
‘λ’ is a wave length.
• The displacement of de Broglie wave associated with a
moving particle along X-direction is given by
)
2
sin( xAS ×=
λ
π
)
2
sin(),( xAtr ×=
λ
π
ψ

52. If ‘E’ is total energy of the
system
)2......(
2
2
2
)(
2
..
2
2
2
2
2
2
VE
m
h
m
h
VE
m
h
V
m
p
VE
EKEPE
−=
+=
+→+=
+=
λ
λ
λ

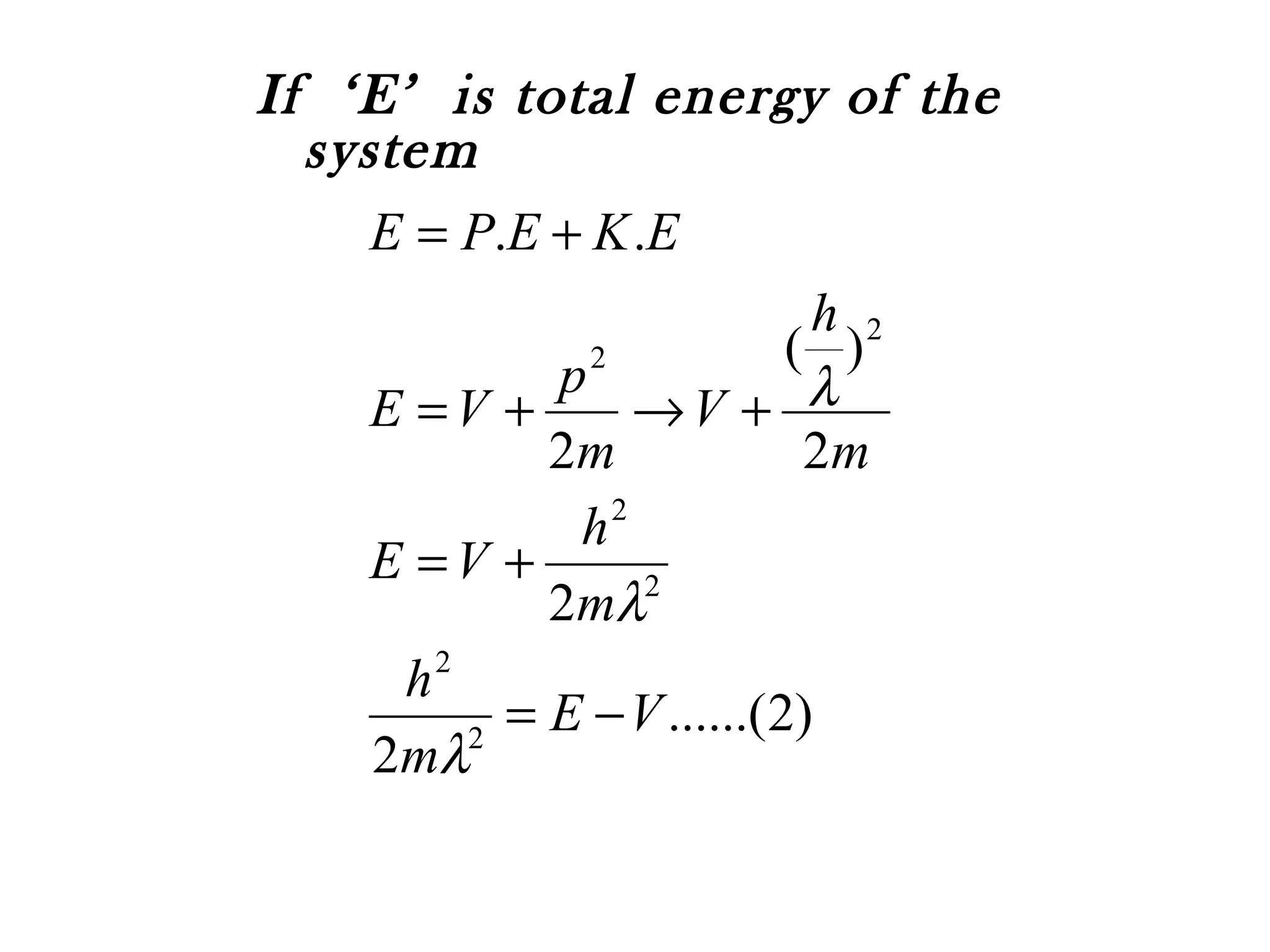
53. Periodic changes in ‘Ψ’ are responsible for the
wave nature of a moving particle
)3(
4
11
4
).
2
sin(
4
).
2
sin(]
2
[
).
2
cos(
2)(
].
2
sin[
)(
2
2
22
2
2
2
2
2
2
2
2
2
2
2
→−=
−=
−=
−=
=
=
dx
d
dx
d
xA
dx
d
xA
dx
d
xA
dx
d
xA
dx
d
dx
d
ψ
ψπλ
ψ
λ
πψ
λ
π
λ
πψ
λ
π
λ
πψ
λ
π
λ
πψ
λ
πψ

54. 0][
8
][
8
][
8
][]
4
1
[
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
=−+
−−=
−=
−
−=−
−=
ψ
πψ
ψ
πψ
ψ
ψπ
ψ
ψπ
λ
VE
h
m
dx
d
VE
h
m
dx
d
VE
dx
d
m
h
VE
dx
d
m
h
VE
m
h
This is Schrödinger time independent wave equation in one dimension.
From equation 3……
0][
8
2
2
2
2
2
2
2
2
=−+
∂
∂
+
∂
∂
+
∂
∂
ψ
πψψψ
VE
h
m
zyx
In three dimensional way it becomes…..

55. Particle in a one dimensional potential
box
• Consider an electron of mass ‘m’ in an infinitely deep one-
dimensional potential box with a width of a ‘ L’ units in
which potential is constant and zero.
Lxxxv
Lxxv
≥≤∞=
〈〈=
&0,)(
0,0)(
X=0 X=L
V=0

56. X
V
∞=V
One dimensional periodic
potential in crystal.
Periodic positive ion cores
Inside metallic crystals.
+ + + + ++ +
+ + + + ++ +
+ + + + ++ +
+ + + + ++ +
+ + + + ++ +

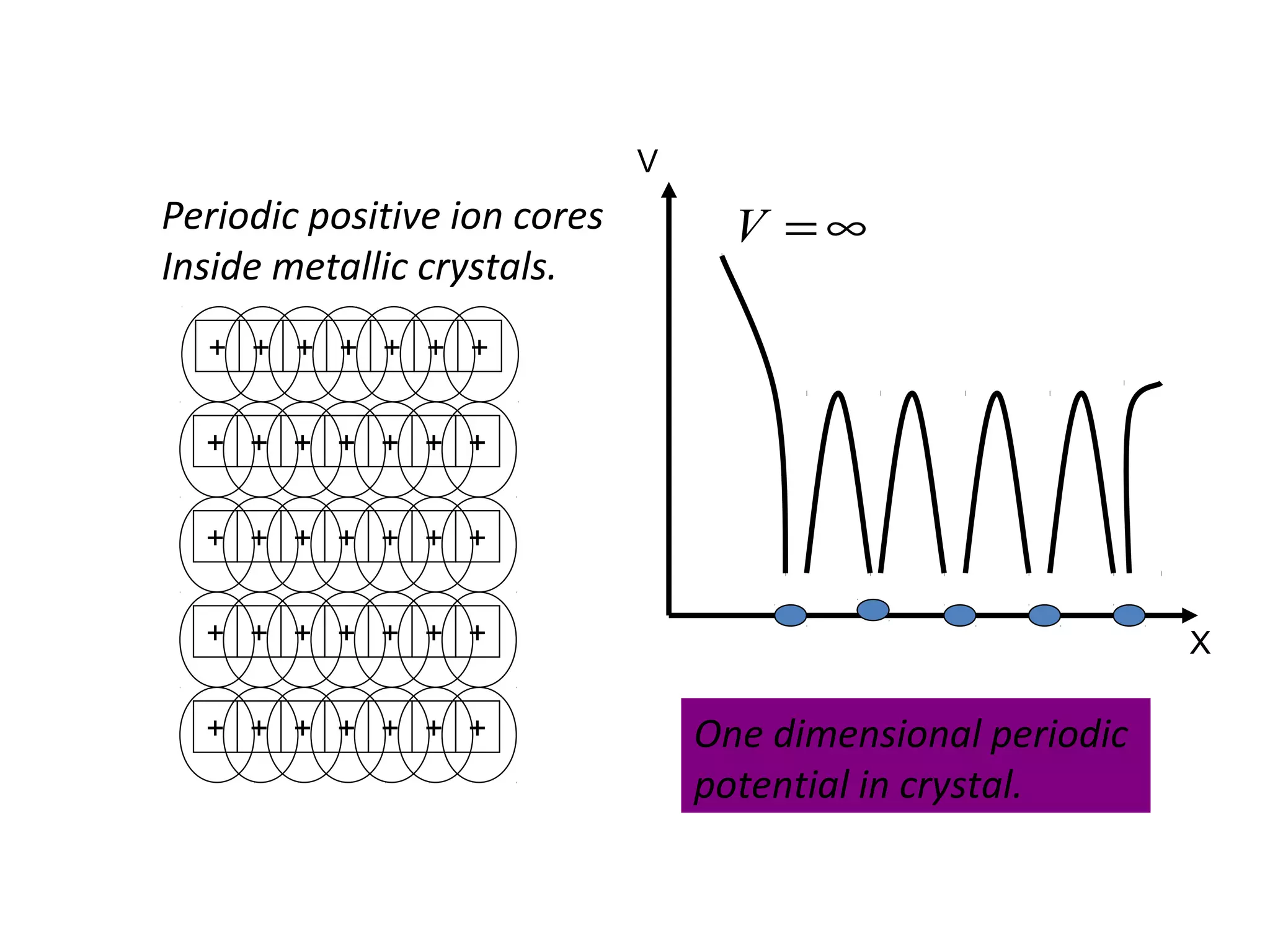
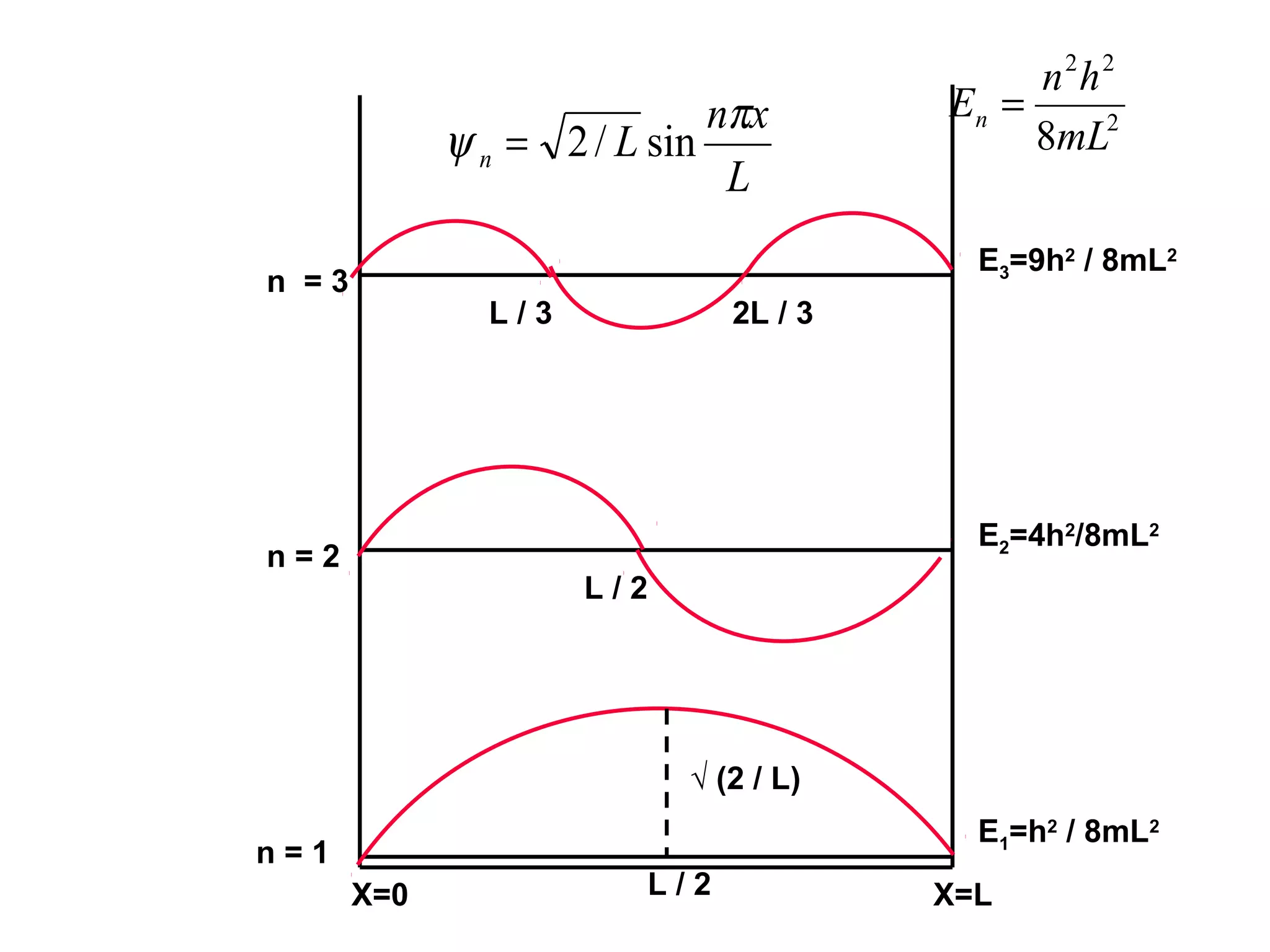
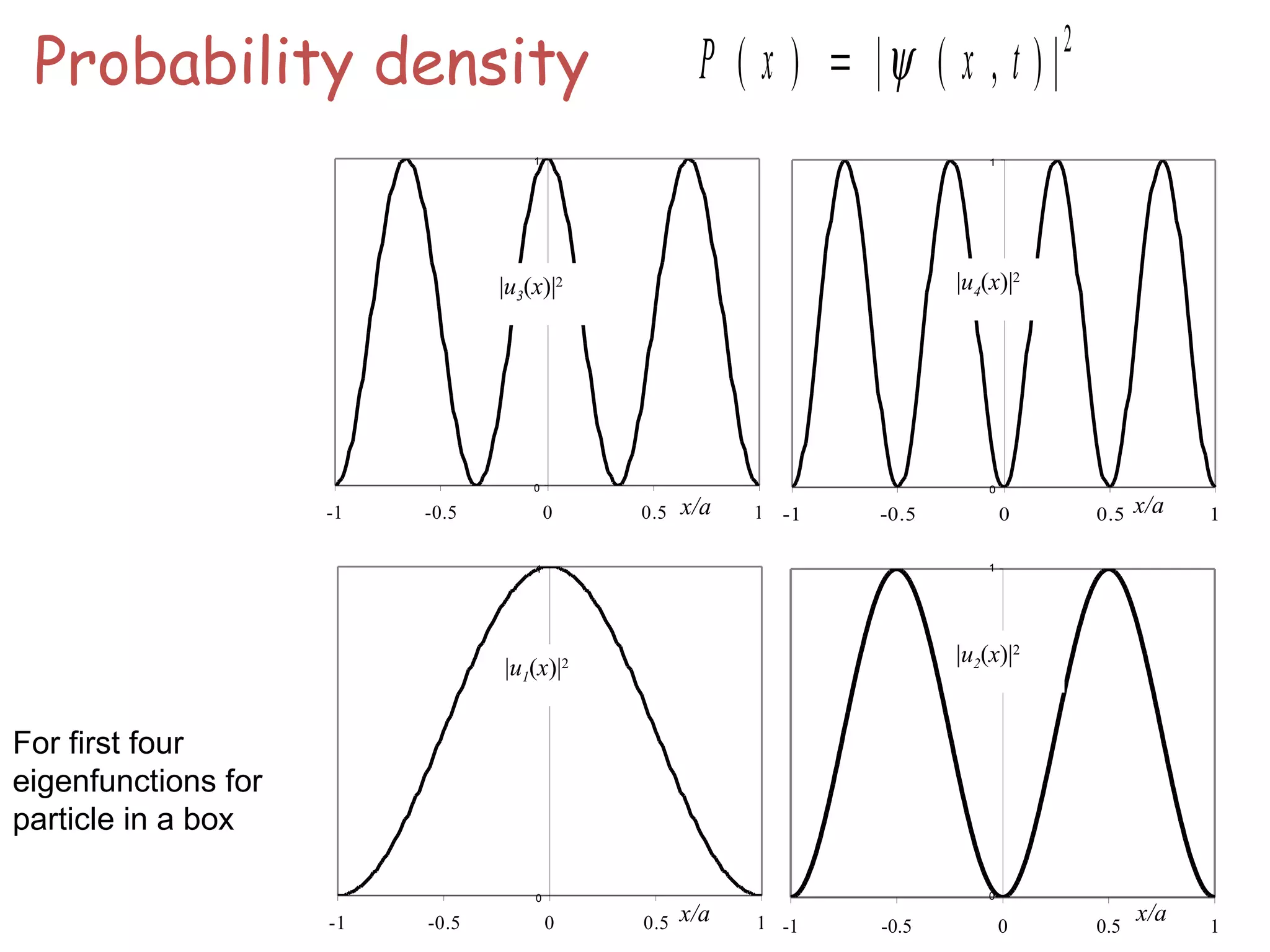
57. The motion of the electron in one dimensional
box can be described by the Schrödinger's
equation.
0][
2
22
2
=−+ ψ
ψ
VE
m
dx
d

Inside the box the potential V =0
E
m
kwherek
dx
d
E
m
dx
d
2
22
2
2
22
2
2
,,0
0][
2


=→=+
=+
ψ
ψ
ψ
ψ
kxBkxAx cossin)( +=ψ
The solution to above equation can be written as

58. Where A,B and K are unknown constants and to
calculate them, it is necessary to apply
boundary conditions.
• When X = 0 then Ψ = 0 i.e. |Ψ|2
= 0 ……. a
X = L Ψ = 0 i.e. |Ψ|2
= 0 …… b
• Applying boundary condition ( a ) to equation ( 1 )
A Sin K(0) + B Cos K(0) = 0 B = 0
• Substitute B value equation (1)
Ψ(x) = A Sin Kx

59. Applying second boundary condition for equation
(1)
Substitute B & K value in equation (1)
To calculate unknown constant A, consider
normalization condition.
L
n
k
nkL
kL
kLA
kLkLA
π
π
=
=
=
=
+=
0sin
0sin
cos)0(sin0
L
xn
Ax
)(
sin)(
π
ψ =

60. The particle Wave functions & their energy
Eigen values in a one dimensional square well
potential are shown in figure.
L
zn
L
yn
L
xn
Ln
πππ
ψ 3213
sinsinsin)/2(=
Normalized Wave function in three dimensions is given by

61. X=0 X=L
E2=4h2
/8mL2
E1=h2
/ 8mL2
E3=9h2
/ 8mL2
n = 1
n = 2
n = 3
L / 2
L / 2
L / 3 2L / 3
√ (2 / L)
2
22
8mL
hn
En =
L
xn
Ln
π
ψ sin/2=

63. Probability density
0
1
-1 -0.5 0 0.5 1
0
1
-1 -0.5 0 0.5 1
0
1
-1 -0.5 0 0.5 1
0
1
-1 -0.5 0 0.5 1
|u1(x)|2 |u2(x)|2
|u3(x)|2 |u4(x)|2
x/a x/a
x/a x/a
P x x t( ) | ( , ) |= ψ 2
For first four
eigenfunctions for
particle in a box

64. Conclusions
1.The three integers n1,n2and n3 called Quantum numbers
are required to specify completely each energy state.
2.The energy ‘ E ’ depends on the sum of the squares of the
quantum numbers n1,n2and n3 but not on their individual
values.
3.Several combinations of the three quantum numbers may
give different wave functions, but not of the same energy
value. Such states and energy levels are said to be
degenerate.

65. Finally, quantum mechanics challenges our assumption that
ultimate reality will accord with our natural intuition about what
is reasonable and normal
Classical physics Quantum physics
I think it is safe to say that no one understands quantum mechanics. Do not keep
saying to yourself, if you can possibly avoid it, 'But how can it possibly be like
that?' … Nobody knows how it can be like that. – Richard Feynman