This document describes a simple method to program shape memory polymer sheets into different two-dimensional shapes using only scissors. The method involves cutting pre-strained polymer sheets into initial shapes and orientations, and then allowing the strain to relax through heating. The final shape is determined by the initial cut orientation relative to the strain direction. Identical initial rectangles cut at different angles take on different final shapes like squares or parallelograms as the strain relaxes. A geometric model is developed to predict the final shapes based on initial dimensions and orientation. Examples demonstrating re-keyable locks and high aspect ratio fibers are also presented.

1. In-plane deformation of shape memory polymer sheets programmed
using only scissors
James R. Allensworth, Ying Liu, Hayley Braun, Jan Genzer*
, Michael D. Dickey*
Department of Chemical & Biomolecular Engineering, North Carolina State University, 911 Partners Way, Raleigh, NC 27695, USA
a r t i c l e i n f o
Article history:
Received 31 May 2014
Received in revised form
24 July 2014
Accepted 25 July 2014
Available online 6 August 2014
Keywords:
Shape morphing
Shape programming
Shape memory polymers
a b s t r a c t
This paper describes an unconventional, yet simple method to program sheets of shape memory polymer
into a variety of two dimensional (2D) structures. The final shape is “encoded” by physically cutting an
initial design out of a pre-strained film. The orientation of the initial cut-out relative to the direction of
strain and the subsequent relaxation of strain via heating defines the final shape. The appeal of the
approach described here is that an easy, low-cost cutting method can achieve a similar shape memory
effect attained by more complex processing techniques. Unlike conventional methods, where the final
shape of a shape memory polymer must be defined a priori, the direction of cutting of the polymer
defines its final shape without any complex pre-programmed strain profiles. A geometric model relating
the resolved 2D polymer shape to the initial shape and strain orientation reveals linear correlation be-
tween the model-predicted and experimentally-observed shapes. In addition to demonstrating the
principle with simple rectangular shapes, we suggest geometries related to encryption and high aspect
ratio fibers.
© 2014 Elsevier Ltd. All rights reserved.
1. Introduction
This paper describes a simple strategy to program polymer
sheets to shape-shift in-plane into a variety of structures in
response to heat. The process begins by cutting (e.g., using scissors)
a pre-strained, inexpensive, chemically-homogeneous, and
commercially available thin polymer sheet into an initial geometry.
Subsequent heating of the polymer above its glass transition allows
the strain to relax, which produces a final shape. The same initial
geometry can produce a variety of programmed shapes by rotating
the orientation of the initial cut-out relative to the strain direction.
This work represents an alternative way to program shape memory
polymers into a variety of geometrical two-dimensional (2D) forms
that may be difficult to fabricate using conventional approaches for
programming shape memory polymers.
Shape memory polymers adopt a pre-programmed shape in
response to an external stimulus, such as, heat, light, or electric
current [1e8]. Advances in shape memory polymers are motivated
by a wide range of applications including textiles [8], healthcare
[9,10], and actuators [2,11]. Fig. 1 illustrates the conventional
approach for programming shape memory polymers and contrasts
it with the alternative approach described here. In the conventional
approach, a polymer network starts in the desired state A, is
deformed while heating to a temporary state B, and is then cooled
to preserve the deformed state B [1,4]. Deformation of A into B
causes stress to build up in the polymer network, and cooling of B
locks-in the stress as a form of stored energy [4,12]. Upon heating
above a triggering temperature (e.g., above the glass transition
temperature), the polymer resorts to the initial state A as the
extended polymer chains relax [13,14].
As depicted in Fig. 1, our method eliminates the complex
deformation of the polymer from the desired state A to the
deformed state B, which requires careful control of stain profiles at
elevated temperatures, and instead defines the final shape B by
cutting shapes from a uniformly deformed polymer sheet. For a
given 2D initial shape, the orientation of the shape with respect to
the strain stored in the specimen dictates the final 2D shape of the
polymer. We note that although the polymer must be deformed in
both cases in Fig. 1, this alternative method achieves shape change
utilizing a uniform strain profile (black arrows in Fig. 1), which is
relatively easy to apply and is a common industrial process.
We demonstrated recently that it is possible to convert a single
shape memory polymer sheet into a wide range of three-
dimensional (3D) shapes by localizing external heating and there-
fore directing the location of relaxation to create a hinging response
* Corresponding authors.
E-mail addresses: Jan_Genzer@ncsu.edu (J. Genzer), mddickey@ncsu.edu
(M.D. Dickey).
Contents lists available at ScienceDirect
Polymer
journal homepage: www.elsevier.com/locate/polymer
http://dx.doi.org/10.1016/j.polymer.2014.07.042
0032-3861/© 2014 Elsevier Ltd. All rights reserved.
Polymer 55 (2014) 5948e5952

2. [15]. The approach here has a similar appeal; it creates a variety of
in-plane (i.e., 2D shapes) from a single pre-strained polymer sheet
that may be fabricated in mass production at low cost. In-plane
shrinkage is useful for a number of applications including heat-
shrink packaging, unconventional fabrication of microfluidic
channels [16], and densification of lithographic features [17,18].
We demonstrate this alternative approach for shape program-
ming, characterize the geometric response, develop a predictive
model, and show a few illustrative examples of the method.
2. Discussion
We chose to use 0.05 mm thick Embrace films manufactured by
Eastman as model substrates because these uniaxially-strained
films are available commercially. These filmsdused industrially as
labels for plastic bottlesdshrink z50e60% in plane (along the di-
rection of strain) when heated above the glass transition temper-
ature (Tg). Polyester films similar to Embrace films quickly reach
ultimate shrinkage without significant heating above Tg [19]. In
some of our experiments, we print patterns of ink on these films to
help visualize shape change and monitor the degree of shrinkage.
This principle is similar to patterns printed on industrially-
produced heat shrink polymer films. However, industrial applica-
tions scale the printed patterns before shrinking so that the final
image does not appear distorted after shrinking.
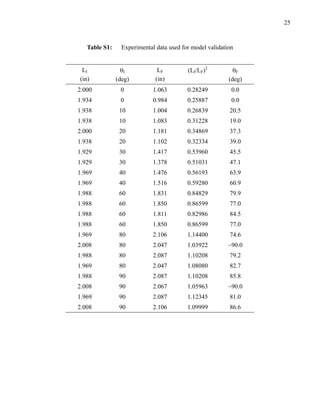
We used a hot water bath at 70 C to induce shrinkage in most of
the samples. We chose this temperature because it is above Tg,
produced significant shrinkage of the polymer sheet in less than a
minute, and provided a relatively safe working temperature (i.e., no
risk of boiling) with minimal evaporation of water. For convenience,
we placed the film samples in the gap of a ‘cartridge’ composed of
two glass slides in a Plexiglass holder (the completed sample
housing is shown in Figures S1 S2 in the Supporting Information)
and submerged it in the water bath. Although the cartridge is not a
necessity, it kept the samples dry during shrinkage. We removed
the samples from the water bath after being submerged for 45 s, at
which point the shrinkage appeared to halt.
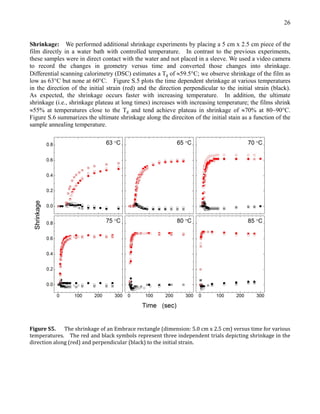
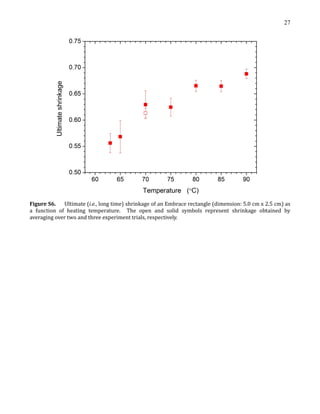
As a concept demonstrator, we cut identical rectangles
(2.5 cm  5 cm) from these films and oriented the cut-outs at an-
gles defined relative to the direction of strain. By arbitrary defini-
tion, an angle of zero degrees aligns the long axis of the rectangle
with the direction of strain. Fig. 2a illustrates the shape and
orientation of the samples, while Fig. 2b provides photographs of
the films before and after heating at 70 C. Black ink from a marker
added to the perimeter of the films after processing enhances
photographic contrast. The Supporting Information (Video S1 and
Figure S3) contains a video capturing the strain relaxation of a
rectangle cut from the film at 45.
Supplementary video related to this article can be found at
http://dx.doi.org/10.1016/j.polymer.2014.07.042.
It is possible to achieve a variety of final shapes from identical
starting patterns by varying only the orientation relative to the
Fig. 1. Comparison of approaches to program the final shape of shape memory polymers. The conventional approach requires managing complex strain profiles at elevated
temperatures, but the alternative approach described here uses only cutting at room temperature to define the final shape. The starting polymer sheet is commercially available and
produced by applying a uniform strain profile.
Fig. 2. (a) Identical rectangles (initial dimension: 2.5 cm  5 cm) cut from a uniaxially
strained film at varied angles relative to the direction of strain. (b) Upon heating above
the glass transition temperature, the identical rectangles (left) resolve into a variety of
final shapes (right). The number listed inside the rectangles refer to the angle of the
long axis of the rectangles relative to the direction of strain.
J.R. Allensworth et al. / Polymer 55 (2014) 5948e5952 5949

3. strain axis. At the two extreme angles, the initial rectangle converts
into a square (at 0, relative to the initial strain direction) and to a
high-aspect ratio rectangle (at 90, relative to the initial strain di-
rection). Intermediate angles convert the same initial rectangle into
parallelograms with different vertex angles. This family of shapes is
unique to the rectangular starting shape; other shapes are possible
with different initial shapes.
Given the stored uniaxial strain in the polymer film, the
shrinkage of a shape of known dimensions and strain angle can be
predicted geometrically. Fig. 3 shows a rectangle with long
dimension before (LI) and after (LF) shrinking. To facilitate
modeling, we define additional terms H and W that correspond to
the resolved vectors of L parallel and perpendicular to the direction
of strain in the film, respectively (Supporting Information,
Figure S4). Before shrinking, the long dimension is oriented at an
angle qI relative to the direction of the initial strain (in this example,
qI ¼ 30). After shrinking, the angle becomes qF.
Equation (1) relates LI and LF to qI, while Equation (2) enables
calculation of qF. The Supporting Information provides the rigorous
mathematical derivation of Equations (1) and (2).
LF
LI
2
¼ S2
H þ
À
S2
W À S2
H
Á
$sin2
qI (1)
qF ¼ sinÀ1À
SW$
LI
LF
$sin qI
Á
(2)
In Equations (1) and (2), Si denotes the shrinkage in the i
dimension (i.e., H or W). Si is defined as:
Si ¼
L0 À L
L0
¼ 1 À
L
L0
; (3)
where L0 and L are the initial and final lengths, respectively, for both
the H and W vectors (note: these lengths are directly related to LI
and LF via geometry). Values of Si 1 correspond to shrinkage and
Si 1 denotes expansion.
To test the model, we measured experimental geometric values
(cf. Fig. 1) and plotted them in Fig. 4. Raw data are included in the
Supporting Information. The best fit of the data in Fig. 4 verifies the
prediction using Equation (1) and enables determination of SH and
SW from the intercept and the slope of the line, respectively. From
the data, we determine SH z 0.512 and SW z 1.046. Thus, upon
heating, the sheet shrinks in the H direction by 48.8% while it ex-
pands in the W direction by 4.6% (cf. Equation (3)).
After completing these experiments, we heated the sheets
directly in a water bath at 70 C (as well as other temperatures, as
reported in Supporting Information Figures S5 S6) for several
minutes to verify the ultimate shrinkage. The ultimate shrinkage
was 60~65% at this temperature and 55.6 ± 1.8% at 63 C, which is
closer to the Tg of the film (59.5 C as verified by DSC). Thus,
samples placed directly in water at temperatures ranging from 63
to 70 C all reached ultimate shrinkages greater than 51.2%, and
notably, required more than 45 s to reach these ultimate shrink-
ages. Data collected from control experiments directly in water at
65 and 70 C reveals that it takes 22e33 and 80~100 s to reach
S ¼ 51.2%, respectively, at these temperatures. Taken in sum, these
results suggest the experiments performed in the plastic sleeve at
70 C had insufficient heating time (45 s) to reach the ultimate
shrinkage. The use of a consistent temperature for a consistent time
resulted in consistent geometric changes even though the samples
did not quite reach the ultimate shrinkage, which is satisfactory for
demonstrating the concept of in-plane shape memory.
The unique shapes that result from the in-plane shape-shift-
ing provide an opportunity to demonstrate new shape memory
concepts. For example, we demonstrate lock-and-key structures
in which the lock and key can both be encoded to be re-keyed
synchronously. We created three “lock-and-key” structures
with identical geometries but cut with different initial orienta-
tions relative to the axis of strain (i.e., qI). We patterned each
structure with a checkerboard design using an inkjet printer to
facilitate observation of the strain relaxation. As shown in Fig. 5,
the contracted samples form “locks” that only mate with their
initial “keys”. In addition to physical structure, the post relaxa-
tion checkerboards are unique to each lock-and-key set, although
the lock and key concept would work equally well without the
ink.
To further demonstrate the utility of shape morphing polymers,
we cut high aspect ratio ‘fibers’ at different strain angles and
relaxed them by heating in an oven. We used an oven because the
long length of the fibers did not fit into the water bath. In response
to heat, and as predicted by the model, the aspect ratio halves for
the 0 fiber, remains the same for the 45 fiber, and doubles for the
90 fiber, as shown in Fig. 6.
Fig. 3. Graphical depiction of the geometric basis used to develop a model that relates
the geometry of the sample to the orientation angle. The images show the geometry of
a sample before (left) and after (right) shrinking induced by heating. Ink is added to the
perimeter of the shapes for visualization and the long axis is colored blue to distin-
guish it. (For interpretation of the references to color in this figure legend, the reader is
referred to the web version of this article.)
Fig. 4. Measured geometric values versus values determined from the geometric
model. The line is a best fit line (LF/LI)2
¼ 0.262 þ 0.831sin2
(qI).
J.R. Allensworth et al. / Polymer 55 (2014) 5948e59525950

4. 3. Summary
We demonstrate and model a new technique to program shape
memory polymers using only cutting to ‘program’ the final shape.
The appeal of this technique is that a single polymer shape cut from
a chemically homogeneous, commercial, pre-strained shape
memory polymer sheet can be converted into a variety of final 2D
shapes using only the orientation of cutting and relaxation of the
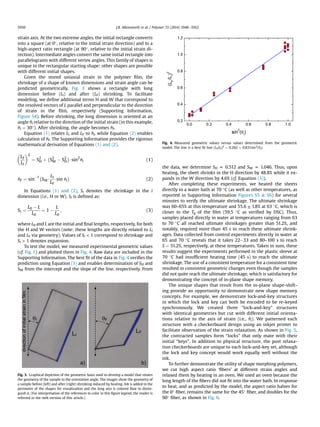
initial strain. We demonstrate an ‘encoded’ lock-and-key structure
in which both the lock and key change in sync depending on the
orientation. Upon heating, the three seemingly identical patterns
resolve into separate shapes, with each having a unique key. As
another demonstration, we fabricated high aspect ratio fibers by
cutting thin fibers at angles greater than 45 and heating above Tg.
Most shape memory polymers start from the desired final
shape, which is physically distorted into a temporary shape that
resorts back to the final shape upon heating. This physical distor-
tion requires careful control of complex strain profiles at elevated
temperatures. Here, we show the ability to define the final shape by
starting with a uniformly distorted sheet that is cut into a ‘pro-
grammed’ shape. This characteristic may be particularly useful for
applications involving shape memory polymers with shapes that
are difficult to pre-program or distort. Although shrink films have
been used in microfabrication and packaging, the work here is the
first to program the final shape by orienting and cutting the initial
geometry relative to the direction of uniaxial strain relaxation.
The approach here could, in principle, apply to any polymer that
can be pre-strained and cut. Although the polymer used here
cannot convert back to the original shape after shrinking, the
approach should apply to other versatile polymers such as cross-
linked, semicrystalline polymers or liquid crystal elastomers with
two-way shape memory effects that provide reversible actuation
[20,21]. Although the approach can produce a variety of shapes, it is
limited by the initial shapes that can be cut. Here, we used scissors,
but it should be possible to achieve more precise shapes by
employing a laser cutter, which has resolution closer to tens of
microns. We also limited ourselves to 2D shapes, but in principle,
the concept could be extended to 3D shapes with appropriate
cutting tools. An appeal of the 2D approach is it should be
compatible with in-plane processes such as lithography, roll-to-
roll, and inkjet printing although the necessity to cut the polymer
is inherently more wasteful than conventional approaches to shape
memory polymers. Ultimately, the shapes created by the technique
described here are limited by the complexity of the starting strain
profiles in the polymer (prior to cutting), but nevertheless, the
simplicity of the approach has appeal as an alternative method for
programming shape memory polymers.
Acknowledgments
We appreciate support from the National Science Foundation
(EFRI ODISSEI grant no. 1240438).
Appendix A. Supplementary data
Supplementary data related to this article can be found at http://
dx.doi.org/10.1016/j.polymer.2014.07.042.
References
[1] Lendlein A, Sauter T. Shape-memory effect in polymers. Macromol Chem Phys
2013;214:1175e7.
[2] Behl M, Razzaq MY, Lendlein A. Multifunctional shape-memory polymers. Adv
Mater 2010;22:3388e410.
[3] Ratna D, Karger-Kocsis J. Recent advances in shape memory polymers and
composites: a review. J Mater Sci 2008;43:254e69.
[4] Liu C, Qin H, Mather PT. Review of progress in shape-memory polymers.
J Mater Chem 2007;17:1543e58.
[5] Behl M, Zotzmann J, Lendlein A. Shape-memory polymers and shape-changing
polymers. In: Lendlein A, editor. Shape-memory polymers. Springer Berlin
Heidelberg; 2010. p. 1e40.
[6] Sun L, Huang WM, Ding Z, Zhao Y, Wang CC, Purnawali H, et al. Stimulus-
responsive shape memory materials: a review. Mater Des 2012;33:577e640.
[7] Leng J, Lan X, Liu Y, Du S. Shape-memory polymers and their composites:
stimulus methods and applications. Prog Mater Sci 2011;56:1077e135.
[8] Hu J, Zhu Y, Huang H, Lu J. Recent advances in shapeememory polymers:
structure, mechanism, functionality, modeling and applications. Prog Polym
Sci 2012;37:1720e63.
[9] Maitland DJ, Metzger MF, Schumann D, Lee A, Wilson TS. Photothermal
properties of shape memory polymer micro-actuators for treating stroke.
Lasers Surg Med 2002;30:1e11.
[10] Behl M, Lendlein A. Shape-memory polymers. Mater Today 2007;10:20e8.
Fig. 5. A photograph of a family of shape-shifting “locks and keys” created by heating
identical patterns cut at qI ¼ 0, 45, and 90 relative to the strain direction. The images
on the right show how the “lock” and “key” deform in sync from the same initial
geometries shown on the left. The red and blue ink is added for visualization purposes.
(For interpretation of the references to color in this figure legend, the reader is referred
to the web version of this article.)
Fig. 6. High aspect ratio polymer strands cut at qI ¼ 0 (red, left), 45 (black, middle),
and 90 (blue, right) relative to the strain direction. The aspect ratio (length/width)
changes can increase or decrease with heating depending on the orientation. (For
interpretation of the references to color in this figure legend, the reader is referred to
the web version of this article.)
J.R. Allensworth et al. / Polymer 55 (2014) 5948e5952 5951

5. [11] Behl M, Kratz K, Noechel U, Sauter T, Lendlein A. Temperature-memory
polymer actuators. Proc Natl Acad Sci U S A 2013;110:12555e9.
[12] Rousseau IA. Challenges of shape memory polymers: a review of the progress
toward overcoming SMP’s limitations. Polym Eng Sci 2008;48:2075e89.
[13] Pakula T, Trznadel M. Thermally stimulated shrinkage forces in oriented
polymers: 1. Temperature dependence. Polymer 1985;26:1011e8.
[14] Trznadel M, Pakula T, Kryszewski M. Thermally stimulated shrinkage forces in
oriented polymers: 2. Time dependence. Polymer 1985;26:1019e24.
[15] Liu Y, Boyles JK, Genzer J, Dickey MD. Self-folding of polymer sheets using
local light absorption. Soft Matter 2012;8:1764e9.
[16] Taylor D, Dyer D, Lew V, Khine M. Shrink film patterning by craft cutter:
complete plastic chips with high resolution/high-aspect ratio channel. Lab
Chip 2010;10:2472e5.
[17] Lee MH, Huntington MD, Zhou W, Yang J-C, Odom TW. Programmable soft
lithography: solvent-assisted nanoscale embossing. Nano Lett 2011;11:
311e5.
[18] Zhang B, Zhang M, Cui T. Low-cost shrink lithography with sub-22 nm reso-
lution. Appl Phys Lett 2012;100:133113.
[19] Shih WK. Shrinkage modeling of polyester shrink film. Polym Eng Sci
1994;34:1121e8.
[20] Meng H, Li G. Reversible switching transitions of stimuli-responsive shape
changing polymers. J Mater Chem 2013;1:7838.
[21] Chung T, Romo-Uribe A, Mather PT. Two-way reversible shape memory in a
semicrystalline network. Macromolecules 2008;41:184e92.
J.R. Allensworth et al. / Polymer 55 (2014) 5948e59525952

6. 19
Supporting Information:
In-Plane Deformation of Shape Memory Polymer Sheets
Programmed Using Only Scissors
James Allensworth, Ying Liu, Hayley Braun, Jan Genzer*, Michael D. Dickey*
Department of Chemical Biomolecular Engineering
North Carolina State University
911 Partners Way
Raleigh, NC 27695, USA
*Corresponding Authors: Jan_Genzer@ncsu.edu, mddickey@ncsu.edu

7. 20
Sample Preparation
Desktop inkjet printers are not capable of printing on Embrace films directly. To print the
checkerboard graphic onto these shrink films, we coated a section of the film substrate with a thin layer
of craft glue (Elmers) and ‘dried’ the coating with a fan at room temperature. To help feed the sheets
through an inkjet printer, we taped the film sections to a thicker 21.6 cm x 28.0 cm plastic sheet.
Scissors cut the desired designs out of the checkerboard printed film.
Water Bath Heating
We used a hot water bath to induce shrinkage in most of the samples, although other heating sources
(e.g., an oven) were used for shrinking the fiber samples due to size restrictions. We placed the film
samples between two poly(dimethylsiloxane)-treated glass slides that allow the sample to shrink in
plane without deforming out of plane. Although we did not anticipate out of plane shrinkage, the
films are thin enough that they can deform unevenly when heated; thus, we confined them between two
glass slides and inserted them inside a Plexiglas ‘cartridge’ (two Plexiglas sheets separated by a small
gap) designed to allow heat transfer but prevent water contact with the film. The dimensions of the
cartridge were such that two glass slides, each 75 mm x 50 mm x 1mm, would loosely fit within the
housing. The completed sample housing is shown in Figure S1, with the glass slides inserted into the
water-proof cartridge.
Figure S1. A polymer sheet patterned with a checkerboard (for visualization) and placed between two
glass slides housed in a Plexiglass cartridge.
As shown in Figure S2, the Plexiglass (polymethylmethacrylate, PMMA) cartridge is immersed in a
water bath at 70°C to relax the strain in the film.

8. 21
Figure S2. Submersion of the sample in 70°C water bath relaxes the strain of the film.
A video capturing the strain relaxation accompanies this supporting information. Screen captures of the
shrinking demonstration video showing pre- and post-relaxation samples are given in Figure S3.

9. 22
Figure S3. A 5.0 cm x 2.5 cm rectangle cut at 45 degrees (top) before shrinking and (bottom) after
shrinking.

10. 23
Geometric Model
The following is a derivation of the geometric model used to determine the sizes of post-relaxation
shapes based on initial lengths and relative strain angles. In each equation, L refers to the length of an
arbitrary line in the same plane as the shrink film. H and W correspond to the resolved vectors of L
parallel and perpendicular to the direction of strain in the film. θ is the angle between L and the strain
direction, while subscripts I and F denote pre- and post-relaxation. Figure S4 denotes graphical
depiction of each quantity.
Figure S4. Graphical depiction of the geometric basis used to develop the model that relates LF
(i.e., dimension before film shrinking, Figure S1a) and LI (i.e., dimension after film shrinking,
Figure S1b) and enables the determination of θF. (a) Before and (b) after shrinking.
L is initially resolved into the two vectors H (parallel to strain) and W (perpendicular to strain) as:
2
F
2
F
2
F WHL += (S1)
HF and WF are related to HI and WI via:
HIF SHH ⋅= (S2)
WIF SWW ⋅= (S3)
In Equations (S2) and (S3), Si denotes the shrinkage in the i direction (i.e., H or W). Si is defined as:
00
0
i 1S
L
L
L
LL
−=
−
= , (S4)
where L0 and L are the initial and final lengths, respectively. Combination of Equations (S1)-(S3)
yields:

11. 24
2
W
2
I
2
H
2
I
2
F SWSHL ⋅+⋅= , (S5)
which after substitution for HI and WI results in:
( ) ( ) 2
WI
22
I
2
HI
22
I
2
F SLSLL ⋅ω⋅+⋅ω⋅= cossin , (S6)
By invoking the law of sines and cosines, Equation (S6) can be rewritten as:
( )( ) ( ) ( ) ( )I
22
H
2
W
2
H
2
WI
22
HI
2
2
I
2
F
SSSSS1
L
L
ω⋅−+=⋅ω+⋅ω−= coscoscos . (S7)
Recognizing that II ω90θ −= 
one can rewrite Equation (S7) as:
( ) I
22
H
2
W
2
H
2
I
F
SSS
L
L
θ⋅−+=





sin . (S8)
The angle θF can be obtained as follows. We first express WI and WF as:
( )III LW ω⋅= cos (S9)
( )FFF oscLW ω⋅= (S10)
By combining Equations (S9)-(S10) with Equation (S3) one arrives at:
( ) ( )F
W
F
II
S
L
L ω⋅=ω⋅ coscos (S11)
Using II ω90θ −= 
and FF ω90θ −= 
one can rewrite Equation (S11) as:
( ) ( )F
W
F
II
S
L
L θ⋅=θ⋅ sinsin , (S12)
which after some algebra yields the expression for θF:






θ⋅⋅= −
I
F
I
W
1
F
L
L
Sinsθ sin (S13)
These derivations provide a predictive tool for use in designing shapes, as the two relevant post-
relaxation quantities (LF and θF) are defined in terms of initial parameters (LI and θI). Desired final
shapes can then be programmed by cutting the related initial designs out of the film. Table S1 lists
experimental data used to plot Figure 4 in the main text and provides estimates of θF.

12. 25
Table S1: Experimental data used for model validation
LI
(in)
θI
(deg)
LF
(in)
(LI/LF)2
θF
(deg)
2.000 0 1.063 0.28249 0.0
1.934 0 0.984 0.25887 0.0
1.938 10 1.004 0.26839 20.5
1.938 10 1.083 0.31228 19.0
2.000 20 1.181 0.34869 37.3
1.938 20 1.102 0.32334 39.0
1.929 30 1.417 0.53960 45.5
1.929 30 1.378 0.51031 47.1
1.969 40 1.476 0.56193 63.9
1.969 40 1.516 0.59280 60.9
1.988 60 1.831 0.84829 79.9
1.988 60 1.850 0.86599 77.0
1.988 60 1.811 0.82986 84.5
1.988 60 1.850 0.86599 77.0
1.969 80 2.106 1.14400 74.6
2.008 80 2.047 1.03922 ~90.0
1.988 80 2.087 1.10208 79.2
1.969 80 2.047 1.08080 82.7
1.988 90 2.087 1.10208 85.8
2.008 90 2.067 1.05963 ~90.0
1.969 90 2.087 1.12345 81.0
2.008 90 2.106 1.09999 86.6

13. 26
Shrinkage: We performed additional shrinkage experiments by placing a 5 cm x 2.5 cm piece of the
film directly in a water bath with controlled temperature. In contrast to the previous experiments,
these samples were in direct contact with the water and not placed in a sleeve. We used a video camera
to record the changes in geometry versus time and converted those changes into shrinkage.
Differential scanning calorimetry (DSC) estimates a Tg of ≈59.5°C; we observe shrinkage of the film as
low as 63°C but none at 60°C. Figure S.5 plots the time dependent shrinkage at various temperatures
in the direction of the initial strain (red) and the direction perpendicular to the initial strain (black).
As expected, the shrinkage occurs faster with increasing temperature. In addition, the ultimate
shrinkage (i.e., shrinkage plateau at long times) increases with increasing temperature; the films shrink
≈55% at temperatures close to the Tg and tend achieve plateau in shrinkage of ≈70% at 80~90°C.
Figure S.6 summarizes the ultimate shrinkage along the direciton of the initial stain as a function of the
sample annealing temperature.
Figure S5. The shrinkage of an Embrace rectangle (dimension: 5.0 cm x 2.5 cm) versus time for various
temperatures. The red and black symbols represent three independent trials depicting shrinkage in the
direction along (red) and perpendicular (black) to the initial strain.

14. 27
Figure S6. Ultimate (i.e., long time) shrinkage of an Embrace rectangle (dimension: 5.0 cm x 2.5 cm) as
a function of heating temperature. The open and solid symbols represent shrinkage obtained by
averaging over two and three experiment trials, respectively.