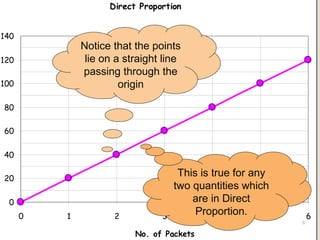
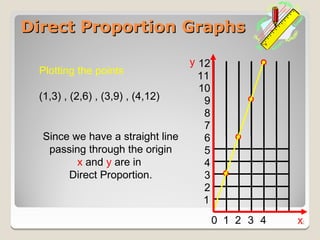
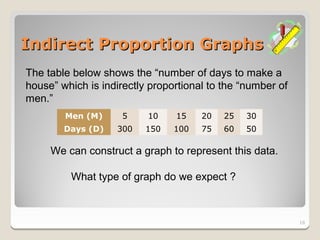
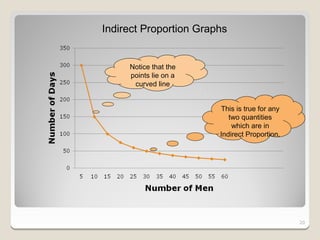
This document discusses direct and inverse proportions. Direct proportion means that as one quantity increases, the other increases by the same ratio. They form a straight line graph passing through the origin. Inverse proportion means that as one quantity increases, the other decreases. The quantities are inversely related by a constant factor. Their relationship forms a curved line graph. Examples of direct and inverse proportions are provided along with their equation representations and graphs. Key features of these graphs are highlighted.

1. Direct and Inverse
Proportion
Chapter 2
(Book 2)
1

2. Direct
Proportion
2

3. Direct Proportion
Two quantities are directly proportional if
an increase in one quantity corresponds to a
constant increase in the other quantity, or if
a decrease in one quantity corresponds to a
constant decrease in the other quantity.
X Y
X Y
3

4. Example:
“Jim’s wages are directly proportional to
the hours he works”
Themore hours he works, the more
money he earns.
This could be written as:
4

5. Wages α Hours
Or...
Wages = k x Hours
k is the “constant of proportionality”
5

6. Direct Proportion Graphs
The table below shows the “cost of packets of Biscuits”
which is directly proportional to the “no. of packets.”
No. of Pkts 1 2 3 4 5 6
Cost (p) 20 40 60 80 100 120
We can construct a graph to represent this data.
What type of graph do we expect ?
6

7. Points to remember for graph:
For the data given in the previous slide
C
∝ N
1. For the above relation N is the independent variable and C is the
dependent variable.
2. On the graph we always take the independent variable on the X axis
and the dependant variable on the Y axis.
7

8. Direct Proportion
140
Notice that the points
120 lie on a straight line Graphs
Direct Proportion
passing through the
100 origin
80
60
40
20
This is true for any
two quantities which
0 are in Direct
0 1 2 3
Proportion. 5
4 6
8
No. of Packets

9. Direct Proportion Graph
KeyPoint
Two quantities which are in
Direct Proportion
always lie on a straight line
passing through the origin.
9

10. Direct Proportion Graphs
Example : Plot the points in the table below.
Are they in Direct Proportion?
X 1 2 3 4
y 3 6 9 12
We plot the points (1,3) , (2,6) , (3,9) , (4,12)
10

11. Direct Proportion Graphs
y 12
Plotting the points 11
10
(1,3) , (2,6) , (3,9) , (4,12) 9
8
7
Since we have a straight line 6
passing through the origin 5
x and y are in 4
Direct Proportion. 3
2
1
0 1 2 3 4 x
11

12. Inverse Proportion
12

13. Inverse Proportion
Two quantities are inversely
proportional if an increase in one
quantity corresponds to a constant
decrease in the other quantity, or if a
decrease in one quantity corresponds to a
constant increase in the other quantity.
X Y
X Y
13

14. Example:
“It takes 4 men 10 days to build a brick
wall. How many days will it take 20 men?”
The more men employed, the less time it
takes to build the wall
Inverse Proportion
14

15. Time is inversely
Proportional to Men
1
t∝ m
15

16. (The first step is to calculate the value of K and form the equation using the
known values)
t= k k
10 =
m 4
k = 4 ×10 = 40
t= 40 (The second step is to use the equation with the
value of K to calculate unknown values)
If we have 20 men, m = 20
m 40
t= = 2 days
20 16

17. Try this when:
M is inversely proportional to R
If M = 9 when R = 4
a. Find M when R =2
b. Find R when M = 3
17

18. Indirect Proportion Graphs
The table below shows the “number of days to make a
house” which is indirectly proportional to the “number of
men.”
Men (M) 5 10 15 20 25 30
Days (D) 300 150 100 75 60 50
We can construct a graph to represent this data.
What type of graph do we expect ?
18

19. Points to remember for graph:
For the data given in the previous slide
M
∝ 1/D
1. For the above relation M is the independent variable and D is the
dependent variable.
2. On the graph we always take the independent variable on the X axis
and the dependant variable on the Y axis.
19

20. Indirect Proportion Graphs
Notice that the
points lie on a
curved line
This is true for any
two quantities
which are in
Indirect Proportion.
20

21. Indirect Proportion Graph
KeyPoint
Two quantities which are
Indirectly Proportion
always make a curved graph.
21

22. If you have any further queries regarding the topic
or have any problems don’t hesitate to ask.
Best of Luck!
22