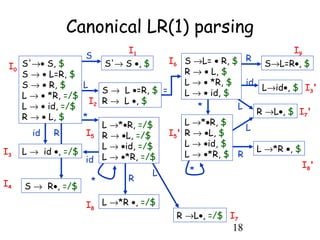
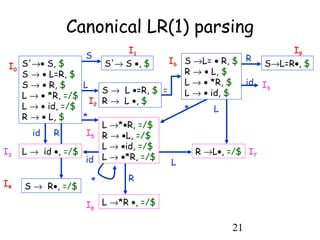
LR parsing techniques include SLR, Canonical LR, and LALR(1) parsing. SLR parsing uses LR(0) items and the FOLLOW set to resolve conflicts, but may introduce conflicts. Canonical LR parsing uses LR(1) items which include lookahead information to avoid conflicts found in SLR parsing. LALR(1) parsing reduces the number of states compared to Canonical LR by merging states with the same core items. LALR(1) can introduce reduce/reduce conflicts, while SLR and Canonical LR can have shift/reduce conflicts.

1. 1
LR parsing techniques
• SLR (not in the book)
– Simple LR parsing
– Easy to implement, not strong enough
– Uses LR(0) items
• Canonical LR
– Larger parser but powerful
– Uses LR(1) items
• LALR (not in the book)
– Condensed version of canonical LR
– May introduce conflicts
– Uses LR(1) items

2. 2
Finding handles
• As a shift/reduce parser processes the input, it
must keep track of all potential handles.
• For example, consider the usual expression
grammar and the input string x+y.
– Suppose the parser has processed x and reduced it to E.
Then, the current state can be represented by E • +E
where • means
• that an E has already been parsed and
• that +E is a potential suffix, which, if found, will result in a
successful parse.
– Our goal is to eventually reach state E+E•, which
represents an actual handle and should result in the
reduction E→E+E

3. 3
LR parsing
• Typically, LR parsing works by building an
automaton where each state represents what has
been parsed so far and what we hope to parse in
the future.
– In other words, states contain productions with dots, as
described earlier.
– Such productions are called items
• States containing handles (meaning the dot is all
the way to the right end of the production) lead to
actual reductions depending on the lookahead.

4. 4
SLR parsing
• SLR parsers build automata where states
contain items (a.k.a. LR(0) items) and
reductions are decided based on FOLLOW
set information.
• We will build an SLR table for the
augmented grammar S'→S
S → L=R
S → R
L → *R
L → id
R → L

5. 5
SLR parsing
• When parsing begins, we have not parsed any input
at all and we hope to parse an S. This is
represented by S'→•S.
– Note that in order to parse that S, we must either parse
an L=R or an R. This is represented by S→•L=R and
S→•R
• closure of a state:
– if A→a•Bb represents the current state and
B→γ is a production, then add B → •γ to the
state.
– Justification: a•Bb means that we hope to see a
B next. But parsing a B is equivalent to parsing a
γ, so we can say that we hope to see a γ next

6. 6
SLR parsing
• Use the closure operation to define states
containing LR(0) items. The first state will be:
• From this state, if we parse, say, an id, then we go
to state
• If, after some steps we parse input that reduces
to an L, then we go to state
S'→• S
S → • L=R
S → • R
L → • *R
L → • id
R → • L
L → id •
S → L •=R
R → L •

7. 7
id
SLR parsing
• Continuing the same way, we define all LR(0) item
states:
S'→• S
S → • L=R
S → • R
L → • *R
L → • id
R → • L
L → id •
S → L •=R
R → L •
S'→ S •I0
I1
I2
I3
S → R •I4
L → *• R
R → • L
L → • id
L → • * R
I5
S
L
*
id R
S → L= • R
R → • L
L → • *R
L → • id
I6
=
R
S → L=R •
R → L •
L
L
I7
id
I3
*
*
L → *R •
R
I8
I9

8. 8
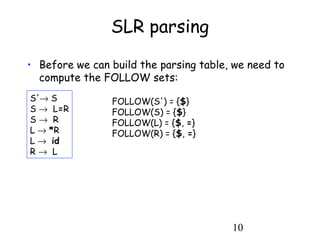
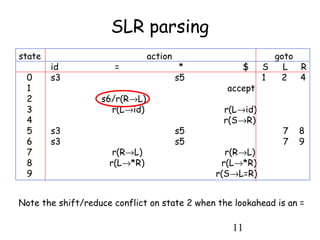
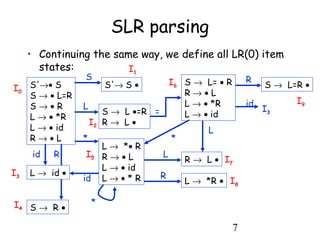
SLR parsing
• The automaton and the FOLLOW sets tell us how
to build the parsing table:
– Shift actions
• If from state i, you can go to state j when parsing a
token t, then slot [i,t] of the table should contain
action "shift and go to state j", written sj
– Reduce actions
• If a state i contains a handle A→α•, then slot [i, t] of
the table should contain action "reduce using A→α",
for all tokens t that are in FOLLOW (A). This is
written r(A→α)
– The reasoning is that if the lookahead is a symbol that
may follow A, then a reduction A→α should lead closer
to a successful parse.
• continued on next slide

9. 9
SLR parsing
• The automaton and the FOLLOW sets tell us how
to build the parsing table:
– Reduce actions, continued
• Transitions on non-terminals represent several steps
together that have resulted in a reduction.
• For example, if we are in state 0 and parse a bit of
input that ends up being reduced to an L, then we
should go to state 2.
• Such actions are recorded in a separate part of the
parsing table, called the GOTO part.

10. 10
SLR parsing
• Before we can build the parsing table, we need to
compute the FOLLOW sets:
S'→ S
S → L=R
S → R
L → *R
L → id
R → L
FOLLOW(S') = {$}
FOLLOW(S) = {$}
FOLLOW(L) = {$, =}
FOLLOW(R) = {$, =}

11. 11
SLR parsing
state action goto
id = * $ S L R
0 s3 s5 1 2 4
1 accept
2 s6/r(R→L)
3 r(L→id) r(L→id)
4 r(S→R)
5 s3 s5 7 8
6 s3 s5 7 9
7 r(R→L) r(R→L)
8 r(L→*R) r(L→*R)
9 r(S→L=R)
Note the shift/reduce conflict on state 2 when the lookahead is an =

12. 12
Conflicts in LR parsing
• There are two types of conflicts in LR parsing:
– shift/reduce
• On some particular lookahead it is possible to shift or
reduce
• The if/else ambiguity would give rise to a shift/reduce
conflict
– reduce/reduce
• This occurs when a state contains more than one handle
that may be reduced on the same lookahead.

13. 13
Conflicts in SLR parsing
• The parser we built has a shift/reduce conflict.
• Does that mean that the original grammar was
ambiguous?
• Not necessarily. Let's examine the conflict:
– it seems to occur when we have parsed an L and are
seeing an =. A reduce at that point would turn the L into
an R. However, note that a reduction at that point would
never actually lead to a successful parse. In practice, L
should only be reduced to an R when the lookahead is
EOF ($).
• An easy way to understand this is by considering that L
represents l-values while R represents r-values.

14. 14
Conflicts in SLR parsing
• The conflict occurred because we made a decision
about when to reduce based on what token may
follow a non-terminal at any time.
• However, the fact that a token t may follow a non-
terminal N in some derivation does not necessarily
imply that t will follow N in some other derivation.
• SLR parsing does not make a distinction.

15. 15
Conflicts in SLR parsing
• SLR parsing is weak.
• Solution : instead of using general FOLLOW
information, try to keep track of exactly what
tokens many follow a non-terminal in each possible
derivation and perform reductions based on that
knowledge.
• Save this information in the states.
• This gives rise to LR(1) items:
– items where we also save the possible lookaheads.

16. 16
Canonical LR(1) parsing
• In the beginning, all we know is that we have not
read any input (S'→•S), we hope to parse an S and
after that we should expect to see a $ as
lookahead. We write this as: S'→•S, $
• Now, consider a general item A→α•Ββ, x. It means
that we have parsed an α, we hope to parse Ββ and
after those we should expect an x. Recall that if
there is a production Β→γ, we should add Β→•γ to
the state. What kind of lookahead should we
expect to see after we have parsed γ?
– We should expect to see whatever starts a β. If β is
empty or can vanish, then we should expect to see an x
after we have parsed γ (and reduced it to B)

17. 17
Canonical LR(1) parsing
• The closure function for LR(1) items is then
defined as follows:
For each item A→α•Ββ, x in state I,
each production Β→γ in the grammar,
and each terminal b in FIRST(βx),
add Β→•γ, b to I
If a state contains core item Β→•γ with multiple
possible lookaheads b1, b2,..., we write Β→•γ, b1/b2
as shorthand for Β→•γ, b1 and Β→•γ, b2

18. 18
id
Canonical LR(1) parsing
L → id •, =/$
S → L •=R, $
R → L •, $
S'→ S •, $I0
I1
I2
I3
S → R•, =/$I4
I5
S
L
*
id R
I6
=
R
S→L=R•, $
R →L•, =/$
L
L
I7
id
*
*
L →*R •, =/$
R
I8
I9
S'→• S, $
S → • L=R, $
S → • R, $
L → • *R, =/$
L → • id, =/$
R → • L, $
L →*•R, =/$
R → •L, =/$
L → •id, =/$
L → •*R, =/$
L→id•, $ I3'
R →L•, $ I7'
S →L= • R, $
R → • L, $
L → • *R, $
L → • id, $
I5'
*
L →*R •, $
I8'
L →*•R, $
R → •L, $
L → •id, $
L → •*R, $
L
R

19. 19
Canonical LR(1) parsing
• The table is created in the same way as
SLR, except we now use the possible
lookahead tokens saved in each state,
instead of the FOLLOW sets.
• Note that the conflict that had appeared
in the SLR parser is now gone.
• However, the LR(1) parser has many more
states. This is not very practical.

20. 20
LALR(1) parsing
• This is the result of an effort to reduce the
number of states in an LR(1) parser.
• We notice that some states in our LR(1)
automaton have the same core items and
differ only in the possible lookahead
information. Furthermore, their transitions
are similar.
– States I3 and I3', I5 and I5', I7 and I7', I8 and I8'
• We shrink our parser by merging such states.
• SLR : 10 states, LR(1): 14 states, LALR(1) : 10 states

21. 21
id
Canonical LR(1) parsing
L → id •, =/$
S → L •=R, $
R → L •, $
S'→ S •, $I0
I1
I2
I3
S → R•, =/$I4
I5
S
L
*
id R
I6
=
R
S→L=R•, $
R →L•, =/$
L
L
I7
id
*
*
L →*R •, =/$
R
I8
I9
S'→• S, $
S → • L=R, $
S → • R, $
L → • *R, =/$
L → • id, =/$
R → • L, $
L →*•R, =/$
R → •L, =/$
L → •id, =/$
L → •*R, =/$
S →L= • R, $
R → • L, $
L → • *R, $
L → • id, $
I3

22. 22
Conflicts in LALR(1) parsing
• Note that the conflict that had vanished
when we created the LR(1) parser has not
reappeared.
• Can LALR(1) parsers introduce conflicts
that did not exist in the LR(1) parser?
• Unfortunately YES.
• BUT, only reduce/reduce conflicts.

23. 23
Conflicts in LALR(1) parsing
• LALR(1) parsers cannot introduce shift/reduce conflicts.
– Such conflicts are caused when a lookahead is the
same as a token on which we can shift. They depend
on the core of the item. But we only merge states
that had the same core to begin with. The only way
for an LALR(1) parser to have a shift/reduce conflict
is if one existed already in the LR(1) parser.
• LALR(1) parsers can introduce reduce/reduce conflicts.
– Here's a situation when this might happen:
A → B •, x
A → C •, y
A → B • , y
A → C •, x
merge with to get: A → B • , x/y
A → C •, x/y

24. 24
Error recovery in LR parsing
• Errors are discovered when a slot in the action
table is blank.
• Phase-level recovery
– associate error routines with the empty table slots.
Figure out what situation may have cause the error and
make an appropriate recovery.
• Panic-mode recovery
– discard symbols from the stack until a non-terminal is
found. Discard input symbols until a possible lookahead
for that non-terminal is found. Try to continue parsing.

25. 25
Error recovery in LR parsing
• Phase-level recovery
– Consider the table for grammar E→E+E | id
+ id $ E
0 e1 s2 e1 1
1 s3 e2 accept
2 e3 e3 r(E→id)
3 e1 s2 e1 4
4 s3 e2 r(E→E+E)
Error e1: "missing operand inserted". Recover by inserting an imaginary
identifier in the stack and shifting to state 2.
Error e2: "missing operator inserted". Recover by inserting an imaginary
operator in the stack and shifting to state 3
Error e3: "extra characters removed". Recover by removing input symbols
until $ is found.

26. 26
LR(1) grammars
• Does right-recursion cause a problem in bottom-up
parsing?
– No, because a bottom-up parser defers reductions until
it has read the whole handle.
• Are these grammars LR(1)? How about LL(1)?
S→Aa | Bb
A→c
B→c
LR(1): YES
LL(1): NO
LL(2): YES
S→Aa | Bb
A→cA | a
B→cB | b
LR(1) : YES
LL(k) : NO
S→Aca | Bcb
A→c
B→c
LR(1): NO
LL(1): NO
LL(2): NO
LR(2): YES