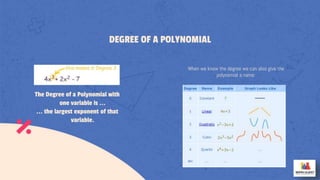
The document provides an introduction to polynomials, detailing their structure including monomials, binomials, and trinomials, along with concepts like degree and roots. It explains methods for finding roots graphically and algebraically, as well as polynomial division using the remainder theorem and factor theorem. The content is designed to be engaging and informative for learners, offering examples to illustrate key concepts.

1. POLYNOMIALSLearning with fun

2. A polynomial looks like this:
INTRODUCTION
A polynomial has:
Variables such as x,y,z with powers as whole
numbers(0,1,2,3…)
Constants like 10

3. 1. Monomial = The polynomial with only one
term. E.g. -2x,5y
2. Binomial = The polynomial with two terms.
E.g. 3x3+5x, 6y+5
3. Trinomial = The polynomial with three terms.
E.g. 4x4+3x2+2, 5y3+4y+9
Types of polynomials

4. When we know the degree we can also give the
polynomial a name:
The Degree of a Polynomial with
one variable is ...
... the largest exponent of that
variable.
DEGREE OF A POLYNOMIAL

5. Solving a
polynomial…
"Solving" means finding the "roots" ...
... a "root" (or "zero") is where the function is equal to zero:

6. WAYS TO FIND ZEROES
1. Graphically
Example: 2x+1
2x+1 is a linear polynomial:
The graph cuts the x-axis at -1/2
which means that at this point
the value of the function y=2x+1
is 0
. Basic Algebra
Example: 2x+1
A "root" is when y is zero: 2x+1 = 0
Subtract 1 from both sides: 2x = −1
Divide both sides by 2: x = −1/2
And that is the solution:
x = −1/2

7. Do you remember doing
division in Arithmetic?
"7 divided by 2 equals 3 with a remainder of 1"
Well, we can divide polynomials in a similar manner
Remainder
Theorem

8. POLYNOMIAL DIVISION EXAMPLE
Example: 2x2−5x−1 divided by x−3
f(x) is 2x2−5x−1
d(x) is x−3
After dividing we get the answer 2x+1, but there is a remainder
of 2.
q(x) is 2x+1
r(x) is 2
In the style f(x) = d(x)·q(x) + r(x) we can write:
2x2−5x−1 = (x−3)(2x+1) + 2
You may refer to our another video “Long
Division Method” to see detailed
explanationKeep in
mind

9. The Remainder Theorem
The Remainder Theorem:
When we divide a polynomial f(x) by x−c the remainder is f(c)
When we divide f(x) by the simple polynomial x−c we get:
f(x) = (x−c)·q(x) + r(x)
x−c is degree 1, so r(x) must have degree 0, so it is just some
constant r :
f(x) = (x−c)·q(x) + r
Now see what happens when we have x equal to c:
f(c) =(c−c)·q(c) + r
f(c) =(0)·q(c) + r
f(c) =r
This is the basis of
remainder theorem…

10. Let’s understand with an example
So to find the remainder after dividing by x-c we don't
need to do any division:
Just find f(c)
We didn't need to
do Long Division at
all!

11. Another example…
Once again…,
We didn't need to
do Long Division at
all!

12. The Factor
Theorem
Now ...
We see this when dividing whole numbers. For example 60 ÷ 20
= 3 with no remainder. So 20 must be a factor of 60.
The Factor
Theorem:
When f(c)=0 then x−c
is a factor of f(x)
And the other way
around, too:
When x−c is a factor
of f(x) then f(c)=0

13. Note…
Knowing that x−c is a factor is the same as knowing that c is a root

14. Does anyone have any questions?
brainquest0127@gmail.com
DM us on Instagram
@brainquestclasses
THANKS!