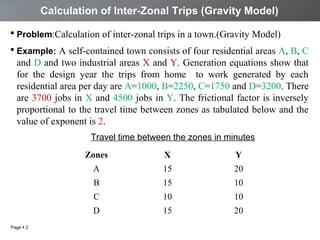
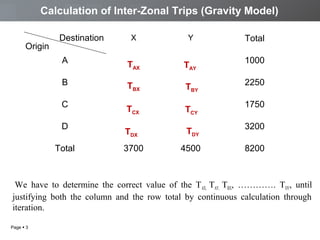
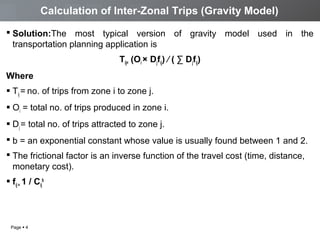
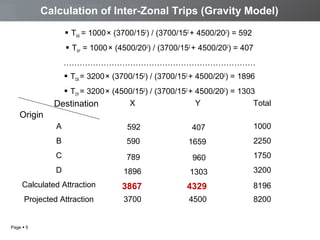
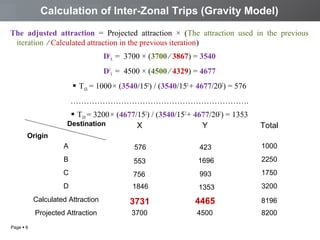
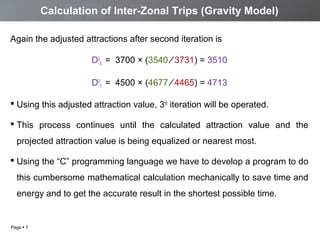
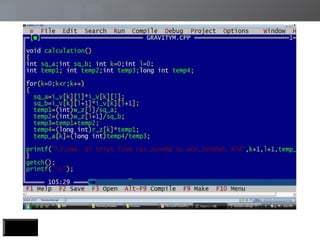
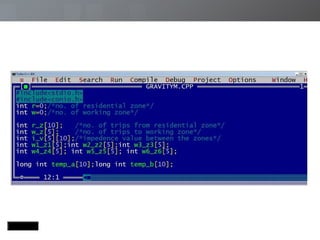
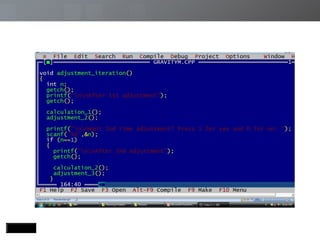
The document discusses a transportation planning problem using the gravity model to calculate inter-zonal trips in a self-contained town with four residential and two industrial areas. It details the method of calculating trips based on job and population data, employing a programming approach in C to automate the iterative calculations needed for accurate trip distribution. The solution includes an explanation of the gravity model formula and outlines the structure of the C program used to perform the calculations efficiently.

1. Solving a Transportation Planning Problem
Through the Programming Language “C”
Presented by
Yousuf Mahid(0615012)
Shahadat Hossain Shakil(0615020)
Khadija Akhter(0615027)

2. Calculation of Inter-Zonal Trips (Gravity Model)
 Problem:Calculation of inter-zonal trips in a town.(Gravity Model)
 Example: A self-contained town consists of four residential areas A, B, C
and D and two industrial areas X and Y. Generation equations show that
for the design year the trips from home to work generated by each
residential area per day are A=1000, B=2250, C=1750 and D=3200. There
are 3700 jobs in X and 4500 jobs in Y. The frictional factor is inversely
proportional to the travel time between zones as tabulated below and the
value of exponent is 2.
Travel time between the zones in minutes
Zones
Y
A
15
20
B
15
10
C
10
10
D
Page  2
X
15
20

3. Calculation of Inter-Zonal Trips (Gravity Model)
Destination
Y
A
TAX
TAY
B
Origin
X
TBX
TBY
TCX
TCY
TDX
TDY
3700
4500
C
D
Total
Total
1000
2250
1750
3200
8200
We have to determine the correct value of the T AX, TAY, TBX, …………. TDY, until
justifying both the column and the row total by continuous calculation through
iteration.
Page  3

4. Calculation of Inter-Zonal Trips (Gravity Model)
 Solution:The most typical version of gravity model used in the
transportation planning application is
Tij= (Oi × Djfij) ∕ ( ∑ Djfij)
Where
 Tij = no. of trips from zone i to zone j.
 Oi = total no. of trips produced in zone i.
 Dj = total no. of trips attracted to zone j.
 b = an exponential constant whose value is usually found between 1 and 2.
 The frictional factor is an inverse function of the travel cost (time, distance,
monetary cost).
 fij = 1 / Cijb
Page  4

5. Calculation of Inter-Zonal Trips (Gravity Model)
 TAX = 1000 × (3700/152) / (3700/152 + 4500/202) = 592
 TAY = 1000 × (4500/202) / (3700/152 + 4500/202) = 407
………………………………………………………………
 TDX = 3200 × (3700/152) / (3700/152 + 4500/202) = 1896
 TDY = 3200 × (4500/152) / (3700/152 + 4500/202) = 1303
X
Y
Total
Destination
Origin
A
592
407
1000
B
590
1659
2250
C
789
960
1750
D
1896
1303
3200
Calculated Attraction
3867
4329
8196
Projected Attraction
3700
4500
8200
Page  5

6. Calculation of Inter-Zonal Trips (Gravity Model)
The adjusted attraction = Projected attraction × (The attraction used in the previous
iteration ∕ Calculated attraction in the previous iteration)
D1X = 3700 × (3700 ∕ 3867) = 3540
D1Y = 4500 × (4500 ∕ 4329) = 4677
 TAX = 1000 × (3540/152) / (3540/152 + 4677/202) = 576
………………………………………………………….
 TDY = 3200 × (4677/152) / (3540/152 + 4677/202) = 1353
Destination
X
Y
Total
Origin
A
423
1000
B
553
1696
2250
C
756
993
1750
D
1846
1353
3200
Calculated Attraction
3731
4465
8196
Projected Attraction
Page  6
576
3700
4500
8200

7. Calculation of Inter-Zonal Trips (Gravity Model)
Again the adjusted attractions after second iteration is
D2X = 3700 × (3540 ∕ 3731) = 3510
D2Y = 4500 × (4677 ∕ 4465) = 4713
 Using this adjusted attraction value, 3rd iteration will be operated.
 This process continues until the calculated attraction value and the
projected attraction value is being equalized or nearest most.
 Using the “C” programming language we have to develop a program to do
this cumbersome mathematical calculation mechanically to save time and
energy and to get the accurate result in the shortest possible time.
Page  7

8. Making Procedure of the Program in “C”
 Divide the whole task among different functions.
 Function declaration.
 Declaring functions prototype before main function.
 Then subdivide the claculation of a specific function into more smaller p
 Variable Declaration-(Local and Global).
 Global Array Declaration- (1D and 2D)-to store and manipulate same
kind of data.
 Function calling - inside the main function and also inside the called
function.
Page  8

9. Making Procedure of the Program in “C”
 Library function used – main(); clrscr(); printf();scanf(); fflush(stdin);
getch(); (including related header files)
 Type of variables used – int; long int; float;
(including ralated format specifier)
 Operator used – arithmatic (addition, multiplication, division)
– assignment(=), relational(==),increment(++)
 Control Statement Used – if statement;
– for loop;
A progarm largely dependent on the use of array and continuous
iteration.
Limitations – deigned for 10 residential zone and 2 working zone.
Failure of converting the fraction trip value into the next higher
integer number.
Page  9

10. Thanks for your patience.
Q/A
Page  10

11. Page  11

12. Page  12

13. Page  13

14. Page  14

15. Page  15