The document provides an overview of data structures and algorithms, specifically focusing on arrays and searching techniques like linear and binary search. It explains how to declare and initialize arrays in C, and details the implementation, time complexities, and methodologies of linear and binary search algorithms. Furthermore, it highlights the efficiency of binary search over linear search when dealing with sorted data structures.

1. Data Structure & Algorithms
Array and Searching
Pre Placement Training- June, 2023 Data Structure & Algorithms 1

2. Outline
2
 Array
 Searching
 Linear Search
 Binary Search

3. Array
An array in C is a fixed-size collection of similar data items stored in contiguous memory locations.
It can be used to store the collection of primitive data types such as int, char, float, etc., and also
derived and user-defined data types such as pointers, structures, etc
3
https://www.geeksforgeeks.org/c-arrays/

4. Array
4
Syntax of Array Declaration
data_type array_name [size];
Or
data_type array_name [size1] [size2]...[sizeN];
where N is the number of dimensions.

5. Array
5
#include <stdio.h>
int main()
{ // array initialization using initialier list
int arr[5] = { 10, 20, 30, 40, 50 };
// array initialization using initializer list without
// specifying size
int arr1[] = { 1, 2, 3, 4, 5 };
// array initialization using for loop
float arr2[5];
for (int i = 0; i < 5; i++) {
arr2[i] = (float)i * 2.1;
}
return 0;}

6. Searching Algorithms
Searching Algorithms are designed to check for an element or retrieve an element from any data
structure where it is stored. Based on the type of search operation, these algorithms are generally
classified into two categories:
• Sequential Search : The list or array is traversed sequentially and every element is checked.
Example: Linear Search
• Interval Search: These algorithms are specifically designed for searching in sorted data-structures.
These type of searching algorithms are much more efficient than Linear Search as they repeatedly
target the center of the search structure and divide the search space in half. For Example: Binary
Search

7. Linear Search
7
https://staragile.com/blog/linear-search

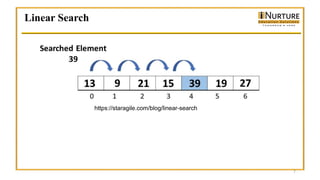
8. Linear Search
#include <stdio.h>
int linear_search(int arr[], int size, int target) {
// Perform linear search
for (int i = 0; i < size; i++) {
if (arr[i] == target) {
return i; // target found at index i
}
}
return -1; // target not found in the array
}
int main() {
int array[] = {4, 2, 7, 1, 9, 5};
int size = sizeof(array) / sizeof(array[0]);
int target_element = 7;
int index = linear_search(array, size, target_element);
if (index != -1) {
printf("Target element found at index %dn", index);
} else {
printf("Target element not found in the arrayn");
}
return 0;
} 8

9. Linear Search
9
The linear_search function takes an array (arr), the size of the array (size), and a target element
(target) as inputs. It iterates through each element of the array using a for loop and checks if the
current element matches the target. If a match is found, it returns the index of the element. If no match
is found after iterating through the entire array, it returns -1 to indicate that the target element was not
found.
The main function demonstrates how to call the linear_search function with an array, its size, and a
target element. It prints the index of the target element if found, or a message stating that the target
element was not found.

10. Linear Search- Time Complexity
10
The time complexity of linear search is O(n), where n represents the number of elements in the array
being searched.
Worst Case: In the worst-case scenario, linear search needs to iterate through all n elements of the
array to find the target element or determine that it is not present. Therefore, the time it takes to
execute linear search grows linearly with the size of the array.
Each element in the array is checked exactly once, resulting in n iterations at most. This makes the
time complexity of linear search proportional to the size of the array, leading to a linear time
complexity of O(n).
It's important to note that in the average case, the time complexity is also O(n) since, on average, the
target element will be found after examining half of the array.

11. Linear Search- Time Complexity
11
Best Case: In the best-case scenario, if the target element is found at the beginning of the array, the
time complexity would be O(1) since the search terminates after just one comparison.

12. Binary Search
12

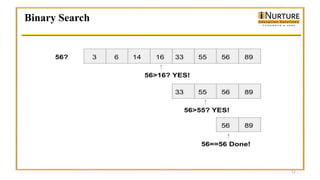
13. Binary Search
#include <stdio.h>
int binarySearch(int arr[], int left, int right, int key) {
while (left <= right) {
int mid = left + (right - left) / 2;
// Check if the key is present at the middle position
if (arr[mid] == key) {
return mid;
}
// If the key is greater, ignore the left half
if (arr[mid] < key) {
left = mid + 1;
}
// If the key is smaller, ignore the right half
else {
right = mid - 1;
}
}
// Key not found
return -1;
}
13

14. Binary Search
int main() {
int arr[] = {2, 5, 8, 12, 16, 23, 38,
56, 72, 91};
int n = sizeof(arr) / sizeof(arr[0]);
int key = 23;
int result = binarySearch(arr, 0, n -
1, key);
if (result == -1) {
printf("Element not found.n");
} else {
printf("Element found at index
%d.n", result);
}
return 0;
}
14

15. Binary Search
15
The binarySearch function performs a binary search on a sorted array. It takes the array, left
index, right index, and the key to be searched as input. It returns the index of the key if found, or -1
if the key is not present in the array.
In the main function, an example array arr is defined, and the size of the array n is calculated. The
key variable represents the element we want to search for in the array. The binarySearch function
is called with the appropriate arguments, and the result is printed accordingly.
Please note that the array arr must be sorted in ascending order for binary search to work correctly.

16. Binary Search- Time Complexity
16
At Iteration 1:
Length of array = n
At Iteration 2:
Length of array = n/2
At Iteration 3:
Length of array = (n/2)/2 = n/22
Therefore, after Iteration k:
Length of array = n/2k

17. Binary Search- Time Complexity
17
Also, we know that after k iterations, the length of the array becomes 1 Therefore, the Length of the
array
n/2k = 1
=> n = 2k
Applying log function on both sides:
=> log2n = log22k
=> log2n = k * log22
As (loga (a) = 1) Therefore, k = log2(n)

18. THANK YOU
18