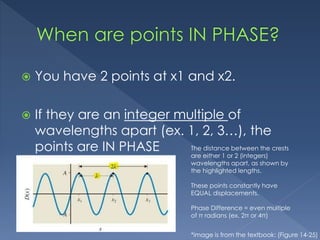
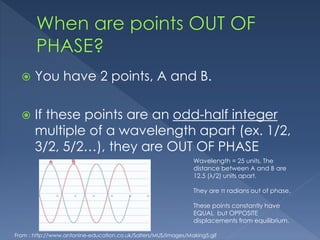
The document discusses phase and phase difference in harmonic waves. It defines phase as the angular argument of a wave's function, measured in radians. Phase difference is the difference in phases between two points on a wave, with a unit of Δφ. The phase difference equation is provided. Two points are in phase if they are an integer multiple of wavelengths apart, and out of phase if they are an odd-half integer multiple apart. An example problem calculating phase difference is worked out.

2.  The angular argument of a harmonic
wave’s function (whether it’s in sine or
cosine) is its PHASE
 Ex.
 Measured in RADIANS, and its unit is phi (ϕ)
 Phase of a general harmonic wave
function:
Highlighted part = phase!
*equations are from the textbook: (Equation 14-16) and (Equation 14-21)

3.  The difference between the phases (of a
harmonic wave’s function) at two
different points is the PHASE DIFFERENCE
 Its unit is Δϕ
 Equation for harmonic waves (where x2
and x1 (denoted as Δx) are different
points on the same wave):
*k = 2π/λ
*equation is from the textbook: (Equation 14-22)

4.  You have 2 points at x1 and x2.
 If they are an integer multiple of
wavelengths apart (ex. 1, 2, 3…), the
points are IN PHASE The distance between the crests
are either 1 or 2 (integers)
wavelengths apart, as shown by
the highlighted lengths.
These points constantly have
EQUAL displacements.
Phase Difference = even multiple
of π radians (ex. 2π or 4π)
*image is from the textbook: (Figure 14-25)

5.  You have 2 points, A and B.
 If these points are an odd-half integer
multiple of a wavelength apart (ex. 1/2,
3/2, 5/2…), they are OUT OF PHASE
From : http://www.antonine-education.co.uk/Salters/MUS/images/Making5.gif
Wavelength = 25 units. The
distance between A and B are
12.5 (λ/2) units apart.
They are π radians out of phase.
These points constantly have
EQUAL but OPPOSITE
displacements from equilibrium.

6. Two points on a wave on a string are 15m
apart.
The wave has a wavelength of 20m.
What is the phase difference between the
two points?

7.  Using Equation 14-22…
 λ = 20m, Δx = 15m, Δϕ = ?
 Δϕ = 2π(15/20)
= 2π(3/4)
= 3π/2 radians.