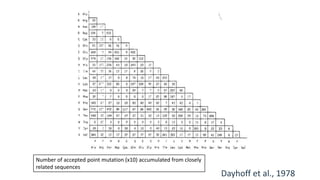
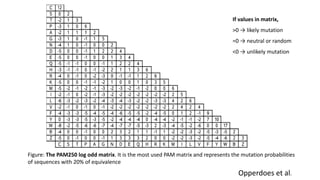
The document discusses the limitations of identity scoring in protein sequence alignment, particularly highlighting its poor diagnostic power due to equal weighting of matches and reliance on simplistic scoring. It introduces the Point Accepted Mutation (PAM) model, conceptualized by Margarett Dayhoff, which provides a more reliable framework for understanding evolutionary changes in proteins through a mutation probability matrix. Additionally, the document details how PAM matrices are constructed, the significance of various amino acid substitutions, and the application of odds matrices in evaluating sequence relationships.

1. PAM
Point Accepted Mutation
PRESENTED BY:
AMITKUMAR KYADA
REG. NO.: 2010119051

2. Limitations of Identity scoring
 In identity scoring we use scoring number 1 and 0.
 It has poor diagnostic power because all identical matches carrying equal weighting.
 In protein sequence alignment and scoring, alphabet size increases from 4 to 20.
 So scoring matrix becomes more complicated in protein than that of DNA.
 Different amino acids partially match in chemical properties, for which Identity scoring (1 and
0) is not reliable.

3. Positive mismatches
• Met → Leu substitution does not
alter the hydrophobic interaction
• Met → Arg substitution alters the
hydrophobic interaction
Hydrophobic interaction between this
Met and Ile stabilizes this binding
• This interaction is essential to cell survival. So in the course of
evolution Met → Leu substitution is more likely to occur than
Met → Arg substitution.
Unit matrix
scheme is
not justified
in this case

4. PAM : Point Accepted Mutation
 Margarett Dayhoff (1978)
 Based on evolutionary distance obtained from 71 closely related protein sequence alignments
 Muataion that comprise of change in single amino acid (substitution) which is accepted by
natural selection. (Accepted point mutation)
 Mutation of gene region (coding single amino acid) to produce different amino acid.
 That mutation accepted as predominant form in a species.
 1 PAM meaning one APM per 100 amino acids.
 It is based on global alignment (aligns entire sequence)

5. PAM : Point Accepted Mutation
 Markovian assumption that each amino acid change at a site being independent of previous
change at that site.
 So we can cover as much as evolutionary divergence as we need (higher PAM unit) by
extrapolating same PAM1 again and again.
• 1 PAM denoted as PAM1
• PAM1 x PAM1 = PAM2
 So generally,
PAMx = PAM1
x ( x iteration of PAM1 )
PAM250 = PAM1
250 (widely used scoring matrices)

6. PAM : Point Accepted Mutation
If we consider PAM100, it does not mean that after 100 PAM of evolution every residue will have
change.
 Some may mutate several times.
 Some may returned to its original state.
 Some residue may not changed at all.

7. PAM matrix origin
• Based on 71 groups of closely related protein.
• PAM (percent accepted mutation) is inferred from the types of changes observed in this
proteins. (tabulated)
• Relative mutability of different amino acids were calculated.
• These two data combined in mutation probability matrix.
• The elements of this matrix give the probability that the amino acid in one column will be
replaced by the amino acid in some row after a given evolutionary interval.
• 0 PAM having ‘ones’ on the main diagonal and ‘zeroes’ elsewhere.
Dayhoff et al., 1978

8. Number of accepted point mutation (x10) accumulated from closely
related sequences
Dayhoff et al., 1978

9. Computation of relative mutability
Dayhoff et al., 1978

10. PAM matrix origin
 Values in mutation probability matrix as follows….
• Non diagonal elements have the value
Where,
Aij is elements of accepted point mutation matrix.
λ is proportionality constant.
Mj is mutability of jth amino acid.
• Diagonal elements have the value
Dayhoff et al., 1978

11. Mutational probability matrix for evolutionary distance of 1 PAM
(for simplification elements are multiplied by 10000)
Dayhoff et al., 1978

12. Mutational probability matrix for evolutionary distance of 250 PAM
(for simplification elements are multiplied by 100)
Dayhoff et al., 1978
As per,
PAMx = PAM1
x ( x iteration of PAM1 )

13. PAM matrix origin
 Relatedness odd matrix
Rij =
𝑴𝒊𝒋
𝒇 𝒊
(odd score matrix)
• when two sequence compared position to position, one should multiply the odds for each
position to get odd score for whole protein.
• So, logarithm (multiplied by 10) of odd matrix is more convenient and used to develop final
log odd matrix (LOD score) (Allows total score of all substitutions by summation)
Where, fi = observed frequency of amino acid Ai
Dayhoff et al., 1978
Here, reciprocal substitution can occur….
A → B = B → A
So, Lod score matrix value filled up by average of
both alternative substitution Lod score.

14. Figure: The PAM250 log odd matrix. It is the most used PAM matrix and represents the mutation probabilities
of sequences with 20% of equivalence
If values in matrix,
>0 → likely mutation
=0 → neutral or random
<0 → unlikely mutation
Opperdoes et al.

15. Correspondence of observed differences between proteins and their evolutionary distance
Greater PAM = greater evolutionary
distance and vice versa.

16. References
 Dayhoff, M., Schwartz, R., & Orcutt, B. (1978). 22 a model of evolutionary change in proteins.
In Atlas of protein sequence and structure (Vol. 5, pp. 345-352).
 PAM matrices. (n.d.). Retrieved May 30, 2020, from
http://www.cs.tau.ac.il/~rshamir/algmb/98/scribe/html/lec03/node9.html
 Bioinformatics tutorial: Construction of substitution matrices part II: PAM matrices 2020.
(n.d.). Retrieved June 1, 2020, from
https://bioinformaticshome.com/bioinformatics_tutorials/sequence_alignment/substitution_
matrices_page2.html
 Opperdoes, Fred & Lemey, Philippe. (2018). Phylogenetic analysis using protein sequences
 PAM Matrices. (n.d.). Retrieved June 2, 2020, from
http://www.quretec.com/u/vilo/edu/2002-
03/Tekstialgoritmid_I/Loengud/Loeng3_Edit_Distance/pam.html

17. THANK YOU…