Kurssilla tarkastellaan ohjelmointikieliä ja paradigmoja teoreettiselta, tekniseltä ja historialliselta kannalta. Aihetta konkretisoidaan tutustumalla eri ohjelmointiparadigmoja edustaviin ohjelmointikieliin. Kurssi luo kokonaiskuvan ohjelmointikielten kehitykseen, minkä jälkeen tarkastellaan lähemmin eri ohjelmointiparadigmoja. Imperatiivisen ohjelmoinnin osalta luodaan kokonaiskuva ohjelmarakenteisiin ja olio-ohjelmoinnin osalta syvennetään ymmärrystä periytymismekanismin ja geneerisyyden toiminnasta. Deklaratiivinen ohjelmoinnin osalta keskitytään erityisesti funktionaaliseen ohjelmointiin ja sen teoreettiseen taustaan (mm. lambda-kalkyyliin) sekä logiikkaohjelmointiin.

1. Jouni Smed
Kevät 2014

2. Yleistä
ž Laajuus: 5 op.
ž Esitiedot (suositus):
— Olio-ohjelmoinnin metodiikka (tai
Sopimuspohjainen olio-ohjelmointi)
ž Kotisivu: bit.ly/okp2014

3. Opetusajat
ž Luennot: tiistaisin 21.1–15.4.2014 klo
12–14 salissa β
— ei 3. periodin viimeisellä viikolla 4.3
ž Demonstraatiot: torstaisin 6.2–27.2.2014
salissa B2039
— ryhmät: 8–10, 10–12, 12–14 ja 14–16

4. Kurssin arvostelu
ž Arvostelu
perustuu 100
pisteeseen
ž Pistejako
— tentti: 60 pistettä
— demonstraatiot:
20 pistettä
— harjoitustyö: 20
pistettä
ž Hyväksytty
kurssi vaatii
yhteensä 45
pistettä
ž Arvosanajako
— [45,55) ⇒ 1
— [55, 65) ⇒ 2
— [65, 75) ⇒ 3
— [75, 85) ⇒ 4
— [85, 100] ⇒ 5

5. Harjoitustyö
ž Tehdään 4. periodissa
ž Arvostelu
— hylätty (0 pistettä)
— välttävä (5 pistettä)
— tyydyttävä (10 pistettä)
— hyvä (15 pistettä)
— kiitettävä (20 pistettä)
ž Lisätietoa muodosta ja suoritustavasta
helmikuun loppupuolella

6. Tentit
ž Sähköinen tentti
— avautuu 5.5.2014
— sulkeutuu 30.9.2014
ž Tentin voi suorittaa enintään kolme (3)
kertaa
ž Lisäohjeita ja ajanvaraus:
https://tenttis.utu.fi

7. Kurssikirjat
ž Smed, Hakonen, Raita:
Sopimuspohjainen olio-ohjelmointi Java-
kielellä, 2007.
ISBN 978-952-92-1776-2
— luvut 5–7 ja 9
ž Scott: Programming Language
Pragmatics, 3rd edition, 2009. ISBN
978-0-12-374514-9
— luvut 9–13

8. Kurssiaikataulu (3. periodi)
Kerta Pvm Aihe
1. 21.1 Ohjelmointiparadigmat
2. 28.1 Olio-ohjelmointi: periytyminen
3. 4.2 Olio-ohjelmointi: periytyminen
(i) 6.2 1. demonstraatiot
4. 11.2 Olion perusoperaatiot ja elinkaari
(ii) 13.2 2. demonstraatiot
5. 18.2 Geneerisyys
(iii) 20.2 3. demonstraatiot
6. 25.2 Olio-ohjelmoinnin erityispiirteitä
(iv) 27.2 4. demonstraatiot

9. Kurssiaikataulu (4. periodi)
Kerta Pvm Aihe
7. 11.3 Funktionaalinen ohjelmointi
8. 18.3 Funktionaalinen ohjelmointi
9. 25.3 Logiikkaohjelmointi
10. 1.4 Rinnakkaisohjelmointi
11. 8.4 Rinnakkaisohjelmointi
12. 15.4 Muita ohjelmointiparadigmoja

10. Kertaus: Kurssin suorittaminen
ž Tentti
— sähköinen tentti 5.5–30.9.2014
— max 60 pistettä
ž Demonstraatiot
— neljä kertaa 3. periodissa
— max 20 pistettä
ž Harjoitustyö
— suoritetaan 4. periodissa
— max 20 pistettä

12. The Jargon File: Programming
programming: n.
1. The art of debugging a blank sheet of paper (or,
in these days of on-line editing, the art of
debugging an empty file). “Bloody instructions
which, being taught, return to plague their
inventor” (Macbeth, Act 1, Scene 7)
2. A pastime similar to banging one's head against a
wall, but with fewer opportunities for reward.
3. The most fun you can have with your clothes on.
4. The least fun you can have with your clothes off.

13. Mitä on ohjelmointi?
ž Luodaan toimintaohjeet (eli lähdekoodi)
joilla tietokone voi suorittaa tietyn
tehtävän tai käyttäytyä tietyllä tavalla

14. Ohjelmointikielten sukupolvet
1. Konekielet
2. Symboliset konekielet (eli assembly-
kielet)
3. Korkean tason ohjelmointikielet
4. Erittäin korkean tason kielet ja
kehitysympäristöt
5. Rajoite- ja logiikkaohjelmointikielet

15. 1. sukupolvi: Konekielet
ž Tietokoneen keskusyksikön suorittamia
käskyjä
— sekvenssi nollia ja ykkösiä
ž Ohjelmointi tapahtui syöttämällä
konekäskyjä binäärimuodossa suoraan
paneelin kautta
0110101

16. 2. sukupolvi: Symboliset
konekielet (eli assembly-kielet)
ž Ohjelmoijan kirjoitettavissa ja luettavissa
— tekstuaalinen esitystapa konekielelle
— makrot
ž Ohjelma käännetään konekielelle
ž Riippuu alustasta
— eri prosessoreilla eri konekielet
lda #$FF
eor $C011,X
bne LOOP

17. 3. sukupolvi: Korkean tason
ohjelmointikielet
ž 1950-luvun lopulla: Fortran, ALGOL,
COBOL
— ihmiskielen kaltaisia
— syntaksi
ž Yhä edelleen suosittuja: C, C#, Java,
BASIC…
ž Käännetään konekielelle tai ajetaan
tulkin kautta
— eivät riipu alustasta VAR Ch: char
BEGIN
WHILE NOT eoln DO
read(Ch)
IF Ch =‘a’ THEN
Res := 0;
ELSE

18. 4. sukupolvi: Erittäin korkean
tason kielet ja kehitysympäristöt
ž Kooditon ohjelmointi
— raporttigeneraattorikielet
— CASE-työkalut
— tiedonhallintatyökalut

19. 5. sukupolvi: Rajoite- ja
logiikkaohjelmointikielet
ž Ongelma kuvataan rajoitteilla
ž Deklaratiivinen ohjelmointi
ž Tietokone ratkaisee ongelman ilman
ohjelmoijaa
min wk’Σwk
s.t. wk’ µ = rk
wki = 1
0 ≤ wk≤ 1

20. Ohjelmointiparadigma
ž Ohjelmointikielen taustalla oleva
perustavanlaatuinen ajattelutapa
— millaisista osista ohjelma rakentuu?
— miten ohjelman suoritus etenee?
ž Ohjelmointikieli voi tukea useaa
paradigmaa

21. Pääparadigmat
Imperatiivinen
ohjelmointi
“Miten päästään
päämäärään”
Deklaratiivinen
ohjelmointi
“Mikä on
päämäärä”

22. Imperatiivinen ohjelmointi 1(2)
ž Taustalla Turingin kone ja von
Neumannin konemalli
— konekielet ovat imperatiivisia
ž Laskenta kuvataan lausekkeina jotka
muuttavat ohjelman tilaa
— ts. käsketään konetta tekemään mitä
ohjelmoija haluaa

23. Imperatiivinen ohjelmointi 2(2)
ž Proseduraalinen ohjelmointi
— aliohjelmat ja funktiot
ž Rakenteellinen (structured) ohjelmointi
— tilan muutokset rajataan aliohjelmien sisälle,
niiden parametreihin ja paluuarvoihin
ž Modulaarinen ohjelmointi
— ohjelman toiminnallisuus rajataan
riippumattomiin, vaihdettaviin moduleihin
ž Oliokeskeinen ohjelmointi
— tiedon kapselointi, periytyminen ja dynaaminen
metodin sidonta

24. Deklaratiivinen ohjelmointi 1(2)
ž Taustalla jokin formaali järjestelmä
— laskenta on dedusointia ko. järjestelmässä
ž Sivuvaikutusten eliminointi (tai ainakin
minimointi)
— parantaa ohjelmiston luotettavuutta
— helpottaa rinnakkaislaskentaa

25. Deklaratiivinen ohjelmointi 2(2)
ž Kyselykielet
— esim. tietokannat
ž Säännölliset ilmaukset
ž Funktionaalinen ohjelmointi
— taustalla lambda-kalkyyli
ž Logiikkaohjelmointi
— taustalla ensimmäisen asteen logiikka

26. Esimerkki: Kakun leipominen…
Imperatiivisesti Deklaratiivisesti
ž Lämmitä uuni 175°C:een.
ž Pehmitä 250 g voita
mikroaaltouunissa.
ž Vaahdota voi ja 250 g sokeria
vaaleaksi vaahdoksi.
ž Lisää 4 kananmunaa pienissä
erissä koko ajan sekoittaen.
ž Yhdistä 5 g leivinjauhetta ja
250 g jauhoja ja lisää ne
vaahtoon.
ž Sekoita kunnolla, mutta ei liian
kovalla teholla.
ž Kaada seos kakkuvuokaan.
ž Paista uunissa 60 minuuttia.

27. Aikajana: 1950- ja 60-luvut
ž FORTRAN
— imperatiivinen (myöh. proseduraalinen)
— asetuslauseet, ehtolauseet, silmukat, I/O (myöh. aliohjelmat)
ž LISP
— funktionaalinen
— taustalla lambda-kalkyyli
ž ALGOL
— proseduraalinen, rakenteellinen
— vaikuttanut suuresti myöhempiin kieliin
ž COBOL
— proseduraalinen
— suunnattu ei-ohjelmoijille
ž Simula
— oliokeskeinen
— esitteli oliot, luokat, aliluokat, virtuaaliset metodit, korutiinit, diskreetin
tapahtumasimuloinnin ja roskienkeruun
ž Muita kieliä: APL, BASIC, LOGO

28. Algol elää!
begin
integer N;
Read Int(N);
begin
real array Data[1:N];
real sum, avg;
integer i;
sum := 0;
for i := 1 step 1 until N do
begin
real val;
Read Real(val);
Data[i] := if val < 0 then -val else val
end;
for i := 1 step 1 until N do
sum := sum Data[i];
avg := sum / N;
Print Real(avg)
end
end

29. Aikajana: 1970-luku
ž Pascal
— rakenteellinen
— tarkoituksena opettaa hyviä ohjelmointikäytäntöjä
ž C
— proseduraalinen, rakenteelinen
— kiinnittyy alla olevaan konekieleen ja laitteistoon
— laajimmalle levinnein ohjelmointikieli
ž Smalltalk
— oliokeskeinen
— kehitetty opetuskäyttöön
— toi olio-ohjelmoinnin yleiseen tietoon ja vaikutti muiden oliokielten
kehitykseen
ž Prolog
— logiikkaohjelmointi
— ohjelmat muodostuvat säännöistä ja kyselyistä
ž Muita kieliä: Forth, SQL, ML, CLU, Scheme, Modula, AWK

30. Aikajana: 1980-luku
ž C++
— proseduraalinen, oliokeskeinen (myöh. funktionaalinen)
— alunperin laajennus C-kieleen: luokat, virtuaaliset funktiot,
ylikuormitus, moniperintä, poikkeukset
— yhä yksi suosituimmista ohjelmointikielistä
ž Ada
— modulaarinen (myöh. oliokeskeinen)
— alunperin sulautettuihin ja reaaliaikaisiin sovelluksiin sekä
suuriin tietojärjestelmiin
ž Perl
— komentosarja, rakenteelinen (myöh. oliokeskeinen)
— vaikutteita monista kielistä: suuri ilmaisunvapaus
ž Muita kieliä: PostScript, occam, Eiffel, Objective-C,
Erlang

31. Aikajana: 1990-luku
ž Java
— rakenteellinen, oliokeskeinen
— alustariippumaton: ohjelma ajetaan tavukoodina
virtuaalikoneessa
— yksi suosituimmista ohjelmointikielistä
ž JavaScript
— komentosarja, rakentellinen, oliokeskeinen
(prototyypit), funktionaalinen
ž Ruby
— oliokeskeinen, funktionaalinen
ž Muita kieliä: Haskell, Python, Lua

32. Aikajana: 2000-luku
ž C#
— rakenteellinen, olio-keskeinen (myöh.
funktionaalinen)
ž Scala
— olio-keskeinen, funktionaalinen
ž Muita kieliä: ActionScript, AspectJ, Io,
Clojure

33. Miksi tutustua erilaisiin
ohjelmointikieliin?
ž Ajatusten esitttämiskyky laajenee
ž Riittävät taustatiedot sopivan
ohjelmointikielen valintaan
ž Kyky omaksua uusia ohjelmointikieliä
ž Kielen toteutuksen merkityksen
ymmärtäminen
ž Kyky seurata, ymmärtää ja arvioida
ohjelmointikielten kehitystä

34. Kuinka ohjelmointikielten
käyttäjät näkevät toisensa…

36. Aiheita
ž Periytyminen
ž Olion perustoimenpiteet ja elinkaari
ž Geneerisyys
ž Asiakas- ja periytymisrelaatiot
ž Aspektit

37. Periytyminen

38. Abstrakti tietotyyppi
ž Abstrakti tietotyyppi (abstract data type,
ADT) kuvaa
— tietoalkion rakenteen
— sille suoritettavat operaatiot
ž ADT antaa tyypille julkisen liitännän
muttei toteutusta
ž Luokka eroaa ADT:stä siinä, että se voi
antaa operaatioille myös toteutuksen

39. Esimerkki: ADT Pino

40. Esimerkki: ADT Jono

41. Periytyminen
ž Olio-ohjelmoinnin keskeinen ajatus on
luokkien muodostama hierarkia
— luokat eivät ole täysin erillisiä kuten rutiinit
proseduraalisessa ohjelmoinnissa
ž Esim: työntekijä on henkilö, jolla on
jotain erityisominaisuuksia, joita ei ole
kaikilla henkilöilla

42. Polymorfismi
ž Tunnisten kyky viitata
moneen erityyppiseen
olioon
Henkilö yksilö;
Työntekijä duunari;
duunari = new Työntekijä("B. Virtanen");
yksilö = duunari;
Työntekijä
Henkilö

43. Alityypitys ja periytyminen
ž Liskovin korvausperiaate: alityypit
käyttäytyvät siten kuin niiden
ylityyppien määrittelyt ilmaisevat
ž Oikeaoppinen tyyppiteorian käyttö
— periytyjä on perimänsä luokan alityyppi
— periytyjä noudattaa perimänsä luokan
operaatioiden määrittelyjä

44. Korvausperiaateen seurauksia
ž Yli- ja aliluokan suhde ei ole symmetrinen
— yliluokka ei voi tietää, mitkä luokat periytyvät (tai
tulevat periytymään) siitä ja mitä piirteitä ne ovat
muokanneet
— siis Henkilö ei voi korvata Työntekijää
ž Yliluokan tyyppiä voidaan kutsua
tietämättä, että kutsutun operaation
toteutus on aliluokassa
— operaation kutsu on siis erotettu suoritettavasta
operaatiosta

45. Staattinen ja dynaaminen tyyppi
1(3)
ž Staattinen tyyppi
— ilmaistaan muuttujan esittelyssä
— pysyy muuttumattomana
ž Dynaaminen tyyppi
— määräytyy sen mukaan minkälaiseen olioon
muuttuja kullakin hetkellä viittaa

46. Staattinen ja dynaaminen tyyppi
2(3)
Henkilö yksilö = new
Työntekijä("Lennart Nilkén");
Työntekijä duunari = new
Työntekijä("B. Virtanen");
ž Dynaaminen tyyppijoukko
— staattisen tyypin ja sen alityyppien
muodostama joukko
— sopivat yhteeen staattisen tyypin kanssa

47. Staattinen ja dynaaminen tyyppi
3(3)
ž Mahdottomia asetuksia kun Henkilö
yksilö ja Työntekijä duunari
— duunari = yksilö;
— yksilö = duunari;
ansio = yksilö.annaPalkka();
ž Yleistulkinta (upcasting)
— yksilö = duunari;
ž Erikoistulkinta (downcasting)
— duunari = (Työntekijä)yksilö;

48. Sidonta
ž Luokka A ja sen perijä B antavat eri
toteutuksen rutiinille f,
ž Luokan A asiakas kutsuu rutiinia
käyttäen muuttujaa x, johon liittyy
polymorfisesti luokan B olio
— ts. A x = new B(); x.f();
ž Mitä tapahtuu?

49. Vaihtoehto 1: Staattinen sidonta
ž Valintapäätös tehdään käännösaikana
— kääntäjä ei voi tietää muuttujan x dynaamista
tyyppiä
— x.f() kutsuu luokan A rutiinia
ž Oletus mm. C++:ssa (ohjelmoijan
muutettavissa: virtuaaliset funktiot)
ž Javassa staattisesti sidotaan
— jäsenmuuttujat
— static-luokkametodit
— final-rutiinit
— private-rutiinit

50. Vaihtoehto 2: Dynaaminen
sidonta
ž Valintapäätös tehdään ajoaikana
— rutiini f valitaan muuttujaan x sillä
hetkellä liitetyn olion tyypin mukaan
— x.f() kutsuu luokan B rutiinia
ž Oletussidonta Javassa
— ei ohjelmoijan muutettavissa

51. C++:n virtuaaliset funktiot
ž Oletuksena C++:ssa metodit sidotaan
staattisesti
ž Mikäli metodi määritetään virtuaaliseksi,
se sidotaan dynaamisesti ajoaikana

52. Esimerkki: Virtuaaliset funktiot
class Perus {
public:
virtual char f() { return 'P'; }
char g() { return 'P'; }
char testaaF() { return f(); }
char testaaG() { return g(); } };
class Johdettu: public Perus {
public:
virtual char f() { return 'J'; }
char g() { return 'J'; } };
main () {
Johdettu j;
print j.testaaF();
print j.testaaG(); }

53. Rutiinin korvaus ja ylikuormitus
ž On mahdollista että aliluokassa määritellään
samanniminen metodi kuin yliluokassa
ž Aliluokka voi korvata (override) yliluokan metodin
— kutsuparametrit samanlaiset kuin yliluokassa
— yliluokan metodia ei enää käytetä aliluokassa tai sen
jälkeläisissä
ž Aliluokka voi ylikuormittaa (overload) metodin
— kutsuparametrit erilaiset
— kyse uudesta metodista, joka ei korvaa vanhaa
ž Milloin on kyse korvauksesta, milloin
ylikuormituksesta?
— kolme vaihtoehtoista sääntöä: kovarianssi, kontravarianssi
ja novarianssi

54. Kovarianssi
ž Kyse on rutiinin korvauksesta, jos
aliluokka muuttaa yliluokan rutiinin
argumenttityypin, tulostyypin ja/tai
poikkeustyypin alityypikseen
ž Esimerkki: jos yliluokassa määritellään
public Number annaNumero()
ja sen aliluokassa
public Integer annaNumero()
kyse on korvauksesta

55. Kontravarianssi
ž Kyse on korvauksesta, jos alityyppi muuttaa rutiinin
argumenttityypin, tulostyypin ja/tai poikkeustyypin
ylityypikseen
ž Esimerkki:
class Kädellinen extends Nisäkäs {
void vertaa(Compable<? super Kädellinen> k {...}
}
class Apina extends Kädellinen {
void vertaa(Compable<? super Nisäkäs> k {...}
}

56. Novarianssi
ž Kyse on korvauksesta, jos tyypit ovat
täsmälleen samat

57. Korvaus
ž Korvauksessa aliluokan toteutus korvaa
yliluokan toteutuksen
ž Javassa rutiinin nimen ja argumenttien
tulee olla samat ja palautustyypin ja
poikkeusten tulee noudattaa
kovarianssisääntöä
ž Korvauksessa suojausmäärettä saa
muuttaa vain väljemmäksi
— muutenhan aliluokka voisi muuttaa jonkin
yliluokan julkisen piirteen privaatiksi…

58. Ylikuormitus
ž Ylikuormituksessa yliluokan metodi ei
korvaudu, vaan se on yhä edelleen
käytettävissä
ž Uusi, samanniminen metodi erotetaan
erilaisten argumenttiensa avulla

59. Lyhyesti: Rutiinien korvaus ja
ylikuormitus
Ta paluutyyppi nimi (argumentit) poikkeukset
Tb paluutyyppi nimi (argumentit) poikkeukset
Ta paluutyyppi nimi (argumentit) poikkeukset
Tb paluutyyppi nimi (argumentit) poikkeukset

60. Luokkatyypit
ž Rajapintaluokka (interface)
ž Abstrakti luokka (abstract class)
ž Konkreetti luokka (concrete class)

61. Rajapintaluokka
ž Luokkamäärittely: interface
ž Ei sisällä rutiinitoteutuksia
ž Kaikki piirteet ovat tyypiltään
— public
— abstract
ž Määrittelee roolin toteuttajille

62. Abstrakti luokka
ž Luokkamäärittely: abstract class
ž Voi sisältää sekä abstrakteja että
konkreetteja rutiineja
ž Ei voida konstruoida!
ž Voi silti toteuttaa konstruktorin
periytymistä varten

63. C++: Puhtaat virtuaaliset metodit
class Puskuri {
public:
virtual int lisaa(char x);
virtual char poista();
};
class Jono : public Puskuri {
public:
Jono() { koko = MAX + 1; etu = taka = 0; }
int lisaa(char) { /* toteutus */ }
char poista() { /* toteutus */ }
private:
char sisalto[MAX + 1];
int koko, etu, taka;
int seur(int i) { return (i + 1) % koko; }
};

64. Konkreetti luokka
ž Luokkamäärittely: class
ž Kaikki piirteet on määritelty
ž Voidaan konstruoida

65. Miksi abstrahoida?
ž Abstrakteista yliluokista on hyvin vähän tai
ei ollenkaan viittauksia muutosalttiisiin
konkreetteihin luokkiin
ž Muut luokat voivat viitata konkreettien
luokkien sijaan näiden abstrakteihin
yliluokkiin ja dynaaminen sidonta huolehtii
kulloisenkin konkreettisen rutiinin
löytymisestä
ž Muutokset konkreettiin toteutukseen eivät
vaikuta korkeimman tason luokkiin
ž Abstraktit luokat muodostavat ohjelmiston
ytimen, johon koko muu ohjelmisto nojaa

66. Luokat pakkauksessa:
abstraktisuus–epävakaus
A
I
(0,1) (1,1)
(1,0)(0,0)

67. Periytyminen
ž Javassa on käytössä
yksittäisperiytyminen
— luokka periytyy yhdestä konkreetista tai
abstraktista luokasta
— luokka voi toteuttaa useita rajapintaluokkia
ž Mikäli luokka määritellään lopulliseksi
(final), siitä ei voi periytyä
— mikäli jokin luokan piirre määritellään
lopulliseksi, periytyjä ei saa muuttaa sitä

68. Luokkahierarkia
ž Javassa kaikki luokat periytyvät
Object-luokasta
— jokaisen olion julkiseen liitäntään kuuluu siis
joukko Object-luokasta periytyviä piirteitä
kuten equals, hashCode, toString
ž Yliluokasta periytyy kaikki paitsi
private-suojausmääreellä varustetut
piirteet
— periytymisessä suojausmääreitä voi
ainoastaan väljentää

69. Javan suojausmääreet
ž public
ž package
ž protected
ž private

70. Suojausmääreiden
vaikutusalueet Javassa
suojaus aliluokka
samassa
pakkauksessa
aliluokka eri
pakkauksessa
ei-periytyvä
luokka
samassa
pakkauksessa
ei-periytyvä
luokka eri
pakkauksessa
private – – – –
package voi käyttää – voi käyttää –
protected voi käyttää voi käyttää voi käyttää –
public voi käyttää voi käyttää voi käyttää voi käyttää

71. C++:n suojausmääreet
ž piirteen suojausmääre
— public
— protected
— private
ž periytymisen suojausmääre
— public
— protected
— private

72. Suojausmääreiden
vaikutusalueet C++:ssa
suojaus periytymis-
tapa
aliluokka aliluokan
asiakas
aliluokan
metodi
aliluokan
perillinen
private – ei voi
käyttää
– – –
protected private private – voi käyttää –
protected protected – voi käyttää voi käyttää
public protected – voi käyttää voi käyttää
public private private – voi käyttää –
protected protected – voi käyttää voi käyttää
public public voi käyttää voi käyttää voi käyttää

73. Moniperiytyminen
ž Moniperiytymisen sallivia kieliä
— C++, Eiffel, Python
ž Yksittäisperitymisen sallivia kieliä
— Simula, Smalltalk, Objective-C
ž “Sekaperitymisen” sallivia kieliä
— Java, C#, Ruby

74. Moniperiytymisen ongelmia
ž Jos kaksi yliluokkaa tarjoaa samannimisen
metodin, kumpaa käytetään aliluokassa?
— voidaanko kutsua vain toista vai kumpaakin?
ž Jos yliluokilla on yhteinen yliluokka, kuinka
monta kertaa se toistuu aliluokassa?
— C++ (oletus): toistettu periytyminen eli useita
kopioita yliyliluokasta
— Eiffel (oletus): jaettu periytyminen eli yksi kopio
yliyliluokasta

75. C++: Moniperiytyminen
ž Oletus: D sisältää kaksi
erillistä A-oliota ja A:n
jäsenet täytyy kvalifioida
ž Jos B:n ja C:n periytymiset
on merkittyy virtuaalisiksi
(class B : virtual public A),
A:sta on yksi olio
ž Jos virtuaalinen ja ei-
virtuaalinen periytyminen
on sekoitettu, on yksi
virtuaalinen A ja yksi ei-
virtuaalinen A
ž Yliluokan piirre täytyy
kvalifioida B::A.f()

76. Käyttö- ja toteutussopimus 1(2)
ž Luokalla on sopimuksia kahteen
suuntaan
— käyttösopimus: luokka takaa asiakkailleen
tietyt palvelut (so. julkinen liitäntä)
— toteutussopimus: luokka takaa aliluokilleen
tietyt palvelut
ž Aliluokan on noudatettava yliluokan
käyttösopimusta
— alkuehtoja voi heikentää ja loppuehtoa
vahventaa

77. Käyttö- ja toteutussopimus 2(2)
Asiakas
Toteuttaja
public
sisäinen
toteutus
private
käyttösopimus
Uudelleen-
käyttäjä
protected,
public
toteutus-
sopimus

78. Esimerkki: Laskuri 1(2)
/** @.classInvariantProtected laskuri on aina
* parillinen
*/
public class ParillinenLaskuri {
protected int laskuri;
public ParillinenLaskuri() {
laskuri = 0;
}
public int annaLaskuriArvo() {
return laskuri;
}
public void kasvataKahdella() {
laskuri += 2;
} }

79. Esimerkki: Laskuri 2(2)
public class YleinenLaskuri
extends ParillinenLaskuri {
public YleinenLaskuri() {
laskuri = 0;
}
public void kasvataYhdellä() {
laskuri++;
} }

80. Periytymisen käyttö
ž Erikoistaminen
— esitetään käsitehierarkia luokkahierarkiana
— ylätason käsite voidaan jakaa useampaan kuin yhteen alatason luokkaan
ž Tarkentaminen
— alatason käsite on sama kuin ylätason käsite
— kiinnitetään toteuttamatta jätetyt piirteet alatasolla
ž Yhdistäminen
— yhdistetään monta eri roolia
— tarkennettu käsite voi esiintyä useammissa rooleissa kuin yliluokka
ž Toteutusperiytyminen
— yläluokalla ei välttämättä ole suoraa suhdetta aliluokkaan
— tarkoituksena välttää samojen operaatioiden kirjoittamista uudelleen,
käyttää niitä työkaluina
ž Ad hoc -periytyminen
— ei luoda laajempaa hierarkiaa, vaan ratkaistaan eteen tullut ongelma
periytymisellä, jos se vaatii vähiten vaivaa

81. Olion perustoiminnot ja elinkaari

82. Olion perustoiminnot
ž Alustus
ž Samuus ja vertailu
ž Kloonaus
ž Viimeistely
ž Vapautus

83. Olion perustoiminnot Javassa
ž Kaikki luokat periytyvät Object-luokasta,
jonka julkinen liitäntä määrittelee joukon
metodeja
— liittyvät abstrakteihin toimintoihin, jotka voivat
kohdata mitä tahansa oliota, esim. kopiointi,
säikeistys, merkkijonoesitys, samuus…
ž Kanoninen olio antaa metodeille järkevät
toteutukset
ž Perustoimintoihin kuuluu myös
alustusoperaatio

84. Alustus 1(2)
ž Konstruktorin nimi on tarkalleen sama
kuin luokan nimi
ž Ei palautusarvoa (ei edes void)
ž Kutsu vain new-operaattorilla
ž Ei periydy (!)
— perivän luokan täytyy määritellä
konstruktori(t) uudestaan
ž Voi kutsua yliluokan konstruktoria
— super(parametrit);
— täytyy olla konstruktorin ensimmäinen
operaatio

85. Alustus 2(2)
ž Oletuksena sama suojausmääre kuin
luokalla
ž Voidaan ylikuormittaa
— voi kutsua toista konstruktoria:
this(parametrit);
ž Mikäli käyttäjä ei ole määritellyt
yhtään konstuktoria, systeemi luo
oletuskonstruktorin
— ei parametreja
— alustaa jäsenmuuttujat oletusarvoihin

86. Esimerkki: konstruktorin
ylikuormitus
class Neliö {
Neliö(int x, int y) {
this(x, y, 10, Color.BLACK);
}
Neliö(int x, int y, int koko {
this(x, y, koko, Color.BLACK);
}
Neliö(int x, int y, int koko, Color väri) {
this.x = x;
this.y = y;
this.koko = koko;
this.väri = väri;
}
}

87. C++:n konstruktori
ž Voidaan ylikuormittaa ja sen
parametreille voidaan antaa oletusarvoja
ž Ei palauta mitään arvoa (ts. sille ei
määritellä paluuarvoa)

88. Esimerkki: C++:n konstruktorit
class Pvm {
public:
Pvm(int, int, int);
Pvm(int, int);
Pvm(int);
Pvm(const char*);
Pvm(); // oletuskonstruktori
private:
int pp_, kk_, vv_;
};
Pvm jokuPaiva(11);
Pvm uusiVuosi("1. tammikuuta 2013");
Pvm tanaan;

89. C++:n erikoiskonstruktorit
ž Oletuskonstruktori
— parametriton
— luodaan implisiittisesti jos luokalle ei ole
määritelty konstruktoreita
— ei luoda, jos konstruktoreita on määritelty
ž Kopiokonstruktori
— käytetään olioiden kopiointiin
— saa parametriksi viittauksen luokan olioon
— luodaan implisiittisesti jos käyttäjä ei ole
määritellyt uuttta toteutusta

90. Olioiden samuus
ž Identtisyys
— ehto a == b on tosi
ž Pintasamuus
— olioiden a ja b jäsenmuuttujat sisältävät
identtiset arvot
ž Syväsamuus
— oliot a ja b ovat pintasamat
— kaikki olioiden a ja b viittaustyyppisistä
vastinjäsenmuuttujista on
rekursiivisesti pintasamat

91. Samanlaisuuden asteet

92. equals-operaation
toteutusvaatimukset
i. Refleksiivisyys: x.equals(x)
ii. Symmetrisyys: x.equals(y) <==> y.equals(x)
iii. Transitiivisuus: x.equals(y) & y.equals(z) ==>
x.equals(z)
iv. Konsistenssi: Jos pintasamuuteen liittyviä tietoja ei muuteta,
vertailun on palautettava johdonmukaisesti tosi tai epätosi
v. Null-epäsamuus: x.equals(null) == false
vi. Rutiinin on toimittava olioiden tyypistä huolimatta.

93. Esimerkki: Henkilö
public boolean equals(Object toinen) {
if (toinen == null) return false;
if (toinen == this) return true;
if (!(toinen instanceof Henkilö)) return false;
Henkilö kaveri = (Henkilö)toinen;
return nimi.equals(kaveri.nimi) &
osoite.equals(kaveri.osoite) &
syntymävuosi == kaveri.syntymävuosi;
}

94. Comparable ja Comparator 1(2)
ž Comparable-rajapinnan määrittelemä
metodi compareTo määrittää oliolle
luonnollisen järjestyksen
— toinen vertailtava on sen rajapinnan toteuttava
luokka itse
ž Comparator-rajapinnan toteuttava luokka
toimii erillisenä vertailijana
— vertailee kahta itsestään erillistä oliota
— voidaan toteuttaa monta erilaista vertailuoliota,
jotka voivat antaa samoille olioille erilaisia
järjestyksiä eri kriteereitten mukaan

95. Comparable ja Comparator 2(2)
ž Vertaillaan kahta samantyyppistä oliota keskenään ja
palautetaan tieto suuruusjärjestyksestä:
a.compareTo(b) tai compare(a, b)
— negatiivinen kokonaisluku, mikäli a on pienempi kuin b
— nolla, mikäli yhtäsuuret
— positiivinen kokonaisluku, mikäli a on suurempi kuin b
— ClassCastException, mikäli a ja b ovat eri tyyppia
ž Huomaa! a.compareTo(b)==0) <==>
(a.equals(b))
— metodeita voidaan käyttää samaan tarkoitukseen

96. Esimerkki: Comparable-
rajapinta
public class Henkilö implements Comparable<Henkilö> {
/* ... */
public int compareTo(Henkilö toinen) {
int tulos = this.nimi.compareTo(toinen.nimi);
if (tulos != 0) return tulos;
if (this.syntymävuosi != toinen.syntymävuosi)
return (this.syntymävuosi <
toinen.syntymävuosi) ? -1 : 1;
else return
this.osoite.compareTo(toinen.osoite);
}
}

97. Kloonaus 1(2)
ž Kloonauksessa oliosta tehdään täysin erillinen
kopio
— ei ole jaettuja olioita millään tasolla
— kopioon tehdyt muutokset eivät vaikuta
alkuperäiseen olion (ja päinvastoin)
ž Mikäli olion jäsenmuuttujat ovat
primitiivityyppejä tai viittauksia
mutatoitumattomiin olioihin, riittää pintakopio
— kopioidaan alkuperäisen olion jäsenmuuttujat ja
olioviittausten muistiosoite
ž Syväkopiossa kopiointioperaatio lähetetään
rekursiivisesti eteenpäin oliossa oleviin
olioviittauksiin

98. Kloonaus 2(2)
ž Kloonaus tehdään clone-metodilla
— vaatii, että luokka toteuttaa Cloneable-rajapinnan
— metodin tulee kutsua yliluokansa clone-metodia
(super.clone) kunnes tullaan Object-luokan
toteutukseen, joka tekee oliosta bitittäisen kopion
— metodi täydentää osaltaan yliluokasta saatua kopiota
ja palauttaa sen kutsujalleen
— mikäli luokka luokka ei toteuta Cloneable-
rajapintaa, metodi heittää CloneNotSupported-
poikkeuksen
ž Huomaa! Jos luokka toteuttaa Cloneable-
rajapinnan, kaikki siitä periytyvät luokat ovat
myös kloonattavissa

99. Esimerkki: Cloneable-rajapinta
public class JangoFett implements Cloneable {
public JangoFett clone() {
try {
return (JangoFett) super.clone();
} catch (CloneNotSupportedException e) {
throw new InternalError(e.toString());
}
}

100. Olioiden kopiointi C++:ssa
ž Sijoitusoperaattori (=)
— oletuksena pintakopio
ž Kopiokonstruktori
— oletuksena pintakopio

101. Esimerkki: kopiointi C++:ssa
class Kopioitava {
public:
Kopioitava() {
// Oletuskonstruktori
}
Kopioitava(const Kopioitava& x) {
// Kopiokonstruktori
}
Kopioitava& operator=(const Kopioitava& x) {
// Sijoitus
}
};

102. Roskien keruu
ž Kun olioon ei ole viittauksia, roskien
keruu (garbage collection) voi poistaa
sen
— ei viittauksia elävistä säikeistä
— ei staattisia viitauksia
— sykliset viittaukset eivät vaikuta
ž Ennen poistoa olio viimeistellään
(finalize)

103. Viimeistely
ž Metodi finalize mahdollistaa olion
varaamien resurssien vapauttamisen
kun olio tuhotaan
— käytännössä tarvitsee toteuttaa erittäin
harvoin

104. Esimerkki: Viimeistely
protected void finalize() throws Throwable {
try {
suljeKaikki();
} finally {
super.finalize();
}
}

105. C++:n destruktori
ž Kutsutaan kun olio tuhotaan
ž Nimi alkaa tilde-merkillä (~) jota seuraa
luokan nimi
ž Ei palauta arvoa
ž Oletusdestruktori luodaan implisiittisesti
mikäli luokalle ei ole annettu destruktoria
— oletustoteutus: vapauttaa jäsenmuuttujille
varatun muistin
ž Tyypillinen käyttötapa on jonkin resurssin
varaaminen ja vapauttaminen

106. Esimerkki: destruktori C++:ssa
class Esimerkki {
public:
Esimerkki(int n = 10) {
n_ = n;
taulukko_ = new int[n];
}
~Esimerkki() {
delete[] taulukko_;
}
private:
int* taulukko_;
int n_;
};

107. Geneerisyys

108. Geneerinen ohjelmointi
ž Ohjelmointia jossa tyypit määritellään
myöhemmin instantioitaessa
parametreina
ž Esiteltiin 1970-luvulla ML-kielessä
— myös CLU ja Ada
ž Tullut osaksi myös oliokeskeisiä kieliä
— Java: geneeriset luokat ja metodit
— C++: mallit (templates)

109. Ada: Geneerinen proseduuri
generic
type Alkio_T is private;
procedure Vaihda (X, Y : in out Alkio_T);
procedure Vaihda (X, Y : in out Alkio_T) is
Apu : constant Alkio_T := X;
begin
X := Y;
Y := Apu;
end Vaihda;
procedure Vaihda_Kokonaisluvut is new Vaihda(Integer);
procedure Vaihda_Liukuluvut is new Vaihda(Float);

110. Ada: Geneerinen pakkaus 1(2)
generic
Max: Positive;
type Alkio_T is private;
package Yleinen_Pino is
procedure Lisaa(A: Alkio_T);
function Poista return Alkio_T;
end Yleinen_Pino;
package body Yleinen_Pino is
Pino: array (1 .. Max) of Alkio_T;
Ylin: Integer range 0 .. Max := 0;
-- jne. jne.
end Yleinen_Pino;

111. Ada: Geneerinen pakkaus 2(2)
declare
package Liukuluku_250_Pino is
new Yleinen_Pino (250, Float);
use Liukuluku_250_Pino;
begin
Lisaa (2.12);
-- jne. jne.
end;

112. C++: Geneerinen luokka mallin
avulla
template<typename T>
class Lista {
/* listan toteutus... */
};
Lista<Elain> elainlista;
Lista<Auto> autolista;

113. C++: Geneerinen metodi mallin
avulla
template<typename T>
void vaihda(T &a, T &b) {
T apu = b;
b = a;
a = apu;
}
string terve = "taas!",
taas = "terve ";
vaihda(taas, terve);
cout << terve << taas << endl;

114. Geneerisyys Javassa
ž Javassa käytössä ovat tyyppiparametrit
— korvataan oikealla tyypillä vasta ajon aikana
— koskevat koko luokkaa tai yhtä metodia
ž Tyyppiparametreja käyttävää luokkaa tai metodia
sanotaan geneeriseksi
ž Esimerkki:
ArrayList<String> omaLista =
new ArrayList<String>();
— sisältää yhden tyyppiparametrin
— tyyppiparametri asetetaan String-tyyppiseksi luotaessa uusi
ArrayList-instanssi
ž Luokkaan voi liittyä useita tyyppiparametreja, jotka
erotetaan pilkulla
— esim. Map<Integer,String> kuvaus =
new HashMap<Integer,String>

115. Geneerinen luokka: määrittely
public class Pari<S,T>
{
private S eka;
private T toka;
public Pari(S e1, T e2)
{
eka = e1;
toka = e2;
}
public S annaEka() { return eka; }
public T annaToka() { return toka; }
public void asetaEka(S e) { eka = e; }
public void asetaToka(T e) { toka = e; }
}

116. Geneerinen luokka: käyttö
Pari<Integer, Integer> p1 =
new Pari<Integer, Integer>(1, 2);
Pari<String, Double> p2 =
new Pari<String, Double>("foo", 43.234);
Pari<Double, Pari<String, String>> p3 =
new Pari<Double, Pari<String, String>>(19.1,
new Pari<String, String>("ab", "ba"));

117. Geneerinen luokka: käyttö Java
7:ssa “timantin” <> avulla
Pari<Integer, Integer> p1 = new Pari<>(1, 2);
Pari<String, Double> p2 = new Pari<>("foo", 43.234);
Pari<Double, Pari<String, String>> p3 = new
Pari<>(19.1, new Pari<>("ab", "ba"));

118. Geneerinen luokka ja metodi
ž Luokka on geneerinen, mikäli se esittelee otsikossaan
tyyppiparametreja
— tyyppiparametrit näkyvät luokan alueella
— myös rajapinta voi esitellä tyyppiparametreja
ž Metodi on geneerinen, mikäli se esittelee signatuurissaan
tyyppiparametreja
— tyyppiparametrit näkyvät metodin sisällä
ž Esimerkki
class Esimerkki {
public <T> void show(T value) {
System.out.println(value);
} }
nyt voidaan kutsua
Esimerkki.<String>show("teksti");
Esimerkki.<Integer>show(42);

119. Tyyppiparametrin rajaus
ž Metodi tai luokka voi rajata
tyyppiparametrinsa
— tyyppiparametrilta voidaan edellyttää tiettyä
roolia tai ominaisuutta
— saa sisältää korkeintaan yhden konkreetin tai
abstraktin luokan
— voi sisältää useita rajapintaluokkia (yhdistetään
&-konnektiivilla)
ž Rajaustyypit
— extends: rajaus ylhäältä päin, minkä luokan
kanssa tyyppiparametrin on oltava yhteensopiva
— super: rajaus alhaalta päin, minkä luokan
yliluokka tyyppiparametrin on oltava

120. Esimerkki: Tyyppiparametrin
rajaus
public class Tasopiste<N extends Number &
Comparable<? super N>> {
private N x, y;
public Tasopiste(N n1, N n2) { x = n1; y = n2; }
public N annaX() { return x; }
public N annaY() { return y; }
public void asetaX(N n) { x = n; }
public void asetaY(N n) { y = n; }
}
Tasopiste<Double> p1 = new Tasopiste<Double>(1.0,
1.3);
Tasopiste<Integer> p2 = new Tasopiste<Integer>(3, -5);

121. Vapaa tyyppi 1(2)
ž Tyyppiparametrit rikkovat ylityyppi–
alityyppi -suhteen
— oletetaan että Koira extends Eläin ja
Kissa extends Eläin
— vaikka List on Collection-luokan
alityyppi, ei List<Koira> ole
Collection<Eläin>-luokan alityyppi
— korvausperiaatteen mukaan List<Koira>-
tyypin pitäisi hyväksyä kaikki kutsut, jotka voi
kohdistaa Collection<Eläin>-tyyppiin

122. Vapaa tyyppi 2(2)
ž Ratkaisu: vapaa tyyppi ?
— esim. Collection<?> on kaikentyyppisten
kokoelmien, kuten List<Koira>-tyypin,
ylityyppi
— voidaan rajoittaa kuten muitakin
tyyppiparametreja: esim. Collection<?
extends Eläin>
ž Toimii myös metodeissa
— String tulosta(List<?> lista)
— String tulosta(List<? extends
Henkilö>)

123. Tyyppitypistys ja raakatyyppi
ž Parametrisoidut tyypit koodiksi
1. koodin erikoistaminen
2. koodin jakaminen
ž Javassa käytössä tapa 2
— tyyppitypistys: kääntäjä poistaa
parametrisoidut tyypit ja rakentaa
tarvittaessa siltametodeja
— tuloksena yksi .class-tiedosto
ž Raakatyyppi: List ≈ List<Object>

124. Geneerisyyden etuja
ž Auttaa keskittymään tietorakenteen
käyttäytymisen toteuttamiseen
ž Helpottaa luokan yleistämistä
ž Johtaa yleiskäyttöisyyteen
— piirrevalikoima määritellään irti spesifistä
kontekstista
ž Tyyppiparametrien ominaisuuksien
määrittely antaa käsityksen geneerisen
luokan roolista luokkahierarkiassa

125. Yleistäminen
ž Toimii kahdella tasolla
— periytymisellä yleistetään mallinnettavia
käsitteitä
— geneerisyydellä yleistetään käsiteltäviä
tietoja
ž Peukalosääntö: Yleistäminen kannattaa
lopettaa viimeistään, kun uusien
asiakkaiden kalastelu aiheuttaa
enemmän työtä kuin nykyisten
asiakkaiden palvelu

126. Periytyminen ja geneerisyys
List<Henkilö>
Collection<Henkilö>
ArrayList<Henkilö>
List<Tasopiste> List<Integer>
Geneerisyys (erikoistaminen)
Periytyminen
YleistäminenErikoistaminen

127. Asiakas- ja periytymisrelaatioista

128. Asiakasrelaatio
ž Asiakas käyttää vain julkisessa
liittymässä kuvattuja piirteitä
ž Olion yksityinen tieto (mm. toteutus) ei
ole asiakkaan käytössä
ž Toteuttaja helposti vaihdettavissa
(kunhan se vain toteuttaa julkisen
liitännän)

129. Periytymisrelaatio
ž Vahvempi suhde sillä aliluokka näkee
yliluokan sisäistä tietoa
ž Aliluokka sidottu yliluokan julkiseen
määrittelyyn (Liskovin korvausperiaate)
ž Mahdollistaa monimutkaisen
käsitehierarkian kuvaamisen

130. Käyttö- ja toteutussopimus
Asiakas
Toteuttaja
public
sisäinen
toteutus
private
käyttösopimus
Uudelleen-
käyttäjä
protected,
public
toteutus-
sopimus

131. Milloin periytyä, milloin olla
asiakas?
ž Peukalosääntö 1: “is-a” vai “has-a”
— periytymien on olemista: “is-a”
— asiakkuus on omistamista: “has-a”
ž Peukalosääntö 2: julkisen liittymän
laajuus
— periytyessä luokka tarjoaa omien
piirteidensä lisäksi kaiken mitä yliluokka
tarjoaa
— asiakkuudessa luokka voi määritellä itse
oman julkisen liittymänsä

132. Is-a vai has-a?
ž Asiakasrelaatio: “has-a”
— Suutari “has-a” Naskali
— muuntuva ja helposti muokattava rakenne
— “has-a” on harvoin “is-a”
ž Periytymisrelaatio: “is-a”
— Suutari “is-a” Työntekijä, Naskali
“is-a” Työkalu
— jähmeä rakenne mutta voi vähentää koodia
— “is-a” on usein “has-a”

133. Esimerkki: Is-a vai has-a?
Työntekijä
Suutari
Työkalu
Naskali

134. Luokkien välisten relaatioiden
edut ja haitat
Ominaisuus Asiakasrelaatio Periytymisrelaatio
Informaation
piilottaminen
Toteutuu Ei yleensä toteudu
Luokkien välinen
riippumattomuus
Saavutetaan Ei saavuteta
Polymorfismi ja
dynaaminen sidonta
Ei toimi Toimii
Luokan toteuttaminen Turhaa painolastia Yksinkertainen

135. Esimerkki: Ympyrä/ellipsi 1(2)
1. Ellipsi extends Ympyrä
— ellipsi on erikoistunut ympyrä
— tyyppiyhteensopivuus: ellipsi “is-a”
ympyrä?
— entäpä piste: Ympyrä extends Piste?
2. Ympyrä extends Ellipsi
— ympyrä on ellipsin erikoistapaus
— ympyrän julkinen liitäntä sisältää ellipsin
käsitteitä?
— entäpä piste?

136. Esimerkki: Ympyrä/ellipsi 2(2)
3. Ympyrä extends Kartioleikkaus,
Ellipsi extends Kartioleikkaus
— ympyrä ja ellipsi ovat kartioleikkauksia
— 3-ulotteinen kappale yliluokkana?
— entä avoimet kartioleikkaukset?
4. YmpyräEllipsi
— kummatkin samassa luokassa
— tehottomat toteutukset?
5. Ympyrä, Ellipsi
— kummatkin omassa luokassaan
— uudelleenkäytön puute?

138. Periaatteita
ž Ilmauksien (funktiokutsujen) arvot
riippuvat ainoastaan niiden argumenttien
arvoista
— ei sivuvaikutuksia (ts. ohjelmointia ilman
asetuslausetta)
ž Uusien ohjelmien (eli funktioiden)
rakentaminen
— kompositio (eli yhdisteleminen)
— rekursio

139. Funktionaalisten kielten
ominaisuuksia
ž Funktiot ovat “ensimmäisen luokan
kansalaisia”
— funktioilla on ohjelmoinnin kannalta sama arvo
kuin muillakin tietoalkioilla
ž Korkeamman asteen funktiot
— käsittelevät ja palauttavat muita (mahdollisesti
suoritusaikana luotuja) funktioita
ž Suoritusjärjestyksen vapaus
— funktiot voidaan evaluoida missä järjestyksessä
tahansa (esim. laiskasti tai rinnakkaisesti)
ž Implisiittinen muistinhallinta

140. Funktionaalisia ohjelmointikieliä
ž Lisp
ž ML
ž Erlang
ž Haskell
ž Scala
ž F#
ž Clojure

141. Lispin perusideat
ž Lambda-kalkyyli
ž Täysin sulutettu puolalainen notaatio
— esim. (+ (* 1 2) 3)
— “Lots of Infuriating, Stupid Parentheses”
ž Linketyt listat ovat tärkein tietorakenne
— LISP = LISt Processing
— Lispin lähdekoodi itsessään on myös lista!

142. Lisp: hyvät ja huonot puolet
ž Syntaksin yksinkertaisuus
— helppo oppia (ohjelmat silti usein vaikealukuisia)
ž Tyypittömyys
— ohjelmat ovat luonnostaan polymorfisia
— tyyppivirheet havaitaan yleensä vasta
suoritusaikana
ž Tulkitseva suoritus
— perinteisesti suoritettu tulkin alaisuudessa
ž Standardin puute
— kymmeniä erilaisia variaatioita eli murteita
— käyttäjän määrittelemien ja systeemin valmiiden
funktioiden välillä ei ole mitään jyrkkää eroa

143. Lispin päämurteet
Scheme
ž minimalismi: kielessä
mahdollisimman
vähän toimintoja;
muut kirjastoissa
ž vaikutteet: lambda-
kalkyyli, Algol ja Lisp
(syntaksi)
ž staattinen
näkyvyysalue, heikosti
tyypitetty
ž sopii
tranformationaaliseen
ohjelmointiin
Common Lisp
ž kokosi yhteen
edeltävien Lisp-
murteiden
ominaisuudet
ž tukee useita
paradigmoja:
imperatiivinen,
funktionaalinen ja
oliokeskeinen
ž dynaaminen tyypitys

144. Esimerkki: Kuutio
(define (kuutio x)
(* x x x)
)
> (kuutio 3)
27

145. Esimerkki: Muunnos sekunneiksi
(define (muunna-sekunneiksi tunnit minuutit)
(* (+ (* tunnit 60) minuutit) 60)
)
> (muunna-sekunneiksi 7 45)
27900

146. Esimerkki: Kertoma
(define (kertoma n)
(cond
((zero? n) 1)
(else (* n (kertoma (- n 1))))
)
)
> (kertoma 4)
24

147. Syntaksi
ž Sulkumerkit
— vaikuttavat ohjelman suoritukseen
ž Prefix-notaatio
— funktio vasemmalla, perässä argumentit
— esim. (+ 1 2 3 4 5)
ž Kommentit: puolipisteestä rivin loppuun
— esim. (kuutio 3) ; kommentti

148. Ilmaukset
ž Primitiiviset
— muuttujat
— literaalit
— ehdot
— funktiot
— funktion kutsut
ž Johdetut
— muiden ilmausten avulla implementoidut
ilmaukset

149. Muuttujat
> (define x 42)
> x
42

150. Literaalit
> (quote x)
x
> 'x
x
> 42
42
> "tere"
"tere"
> #t
#t

151. Aritmeettiset funktiot
ž +, -, *, / ja rem
ž Yhteen- ja kertolasku voidaan kohdistaa
kuinka moneen argumenttiin tahansa
— esim. (+ 1 2 3) tai (* 4 5 6 7 8)

152. Testifunktiot
ž (equal? L M)
— ovatko L ja M rakenteeltaan samanlaiset
ž (eq? L M)
— viittaavatko L ja M samaan ilmaukseen
ž (atom? A), (pair? A), (null? A),
(number? A)
— ilmauksen tyypin (tai arvon) testaus.
ž (= L M), (< L M), (> L M)
— aritmeettiset vertailut
ž Testifunktioiden tulos
— atomi #t mikäli ominaisuus on voimassa
— atomi #f mikäli ei ole

153. Totuusfunktiot
ž (not L)
— toteutuu mikäli L evaluoituu epätodeksi
ž (and L1 … Lk)
— toteutuu, mikäli kaikki argumentit evaluoituvat
tosiksi
— oikosulkuevaluointi
ž (or L1 … Lk)
— toteutuu, mikäli yksikin argumentti evaluoituu
todeksi
— oikosulkuevaluointi
ž totuusarvoja edustavat atomit #t ja #f

154. Ehdolliset ilmaukset: if
ž (if ehto seuraus)
ž (if ehto seuraus vaihtoehto)
ž Esimerkki:
(if (< x y)
(kuutio x)
(kuutio y))

155. Ehdolliset ilmaukset: cond
ž (cond (ehto1 seuraus1)
(ehto2 seuraus 2)
…
(else vaihtoehto))
ž Esimerkki:
(cond ((< x 0) 'negatiivinen)
((> x 0) 'positiivinen)
(else 'nolla))

156. Lambda-kalkyyli
ž Formalismi matemaattisten funktioiden
käsittelyyn
— yksinkertaisin mahdollinen tapa mallintaa
funktioiden määrittely ja soveltaminen
ž Formalismissa tarvitaan
— muuttujien joukko x, y, z…
— sulut
— symboli λ

157. Lambda-ilmausten määrittely
1. Muuttujat ovat λ-ilmauksia.
2. Jos M on λ-ilmaus ja x muuttuja, niin λx M
on λ-ilmaus.
3. Jos M ja N ovat λ-ilmauksia, niin (M N) on
λ-ilmaus.

158. Sidottu ja vapaa muuttuja
ž Muuttujan x esiintymä ilmauksessa M on
sidottu, jos se sisältyy muotoa λx N
olevaan M:n osailmaukseen
ž Jos muuttujan esiintymä ei ole sidottu,
se on vapaa

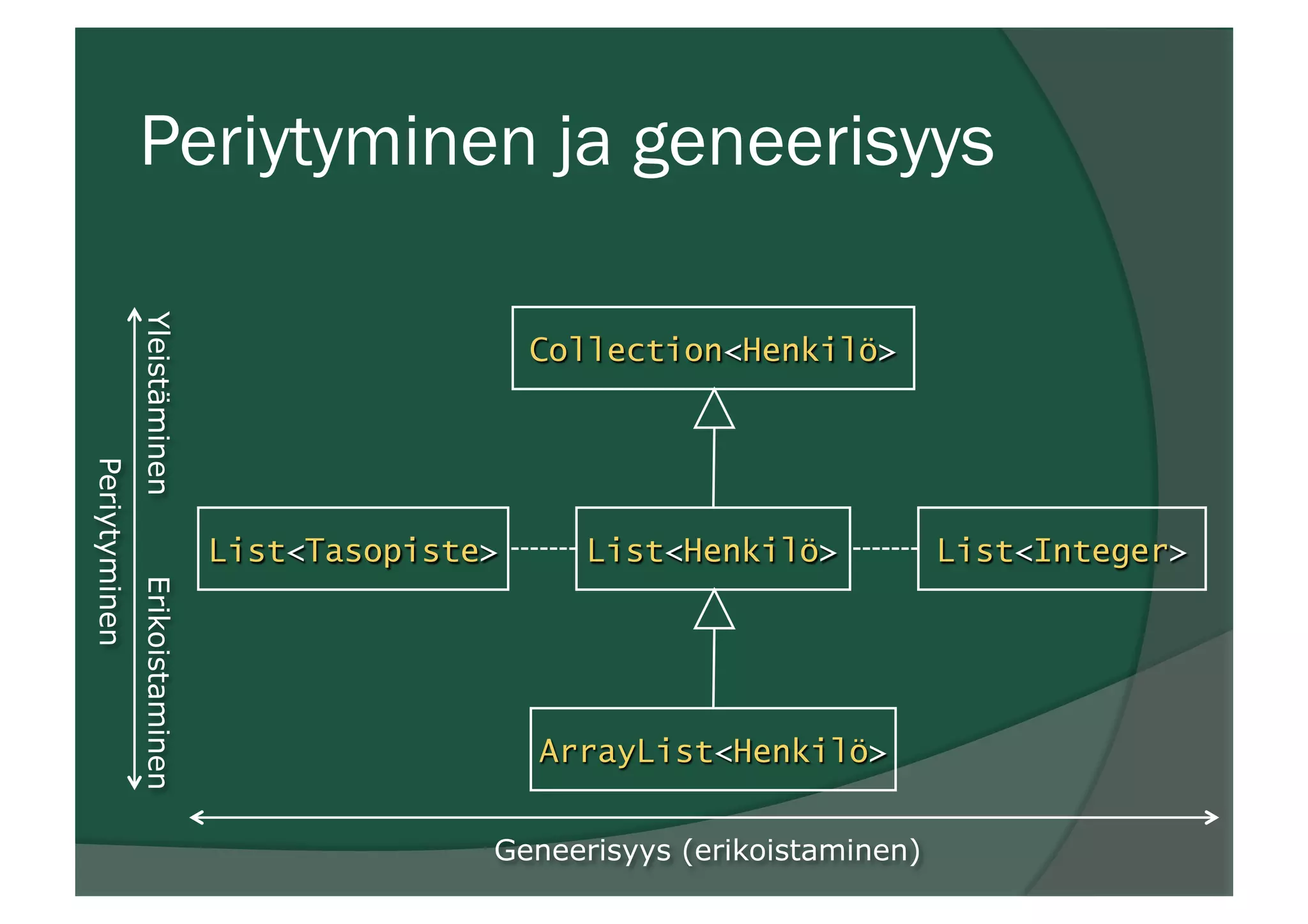
159. Ilmausten muuntaminen
ž M[x/N] tarkoittaa että ilmauksessa M
korvataan kaikki muuttujan x vapaat
esiintymät ilmauksella N.
ž Muunnossäännöt:
— reduktio
— korvaus

160. Reduktio
ž Ilmaus (λx M N) redusoituu ilmaukseksi
M[x/N]
ž Reduktiosäännön soveltaminen vastaa
parametrin N välittämistä funktiolle M
— ts. x on muodollisen parametrin nimi

161. Korvaus
ž Ilmaus λx M redusoituu ilmaukseksi λy
M[x/y]
ž Korvaussäännön avulla voidaan
tarvittaessa uudelleennimetä funktion
parametri, jotta reduktiosääntöä voidaan
soveltaa (vrt. nimiparametrin välitys)
— ei tarvita, jos muuttujanimet ovat
yksikäsitteisiä

162. Redusointi
ž λ-ilmaus on redusoitu, mikäli siihen ei voida
soveltaa reduktiosääntöä, vaikka kaikki
muuttujat nimettäisiin uudelleen
— redusoitu muoto vastaa ilmauksen esittämän
funktion arvoa
— redusointi on funktion arvon laskemista eli
evaluointia
ž Churchin–Rosserin teoreema: Jokaisella
redusoituvalla λ-ilmauksella on
yksikäsitteinen redusoitu muoto
— ei takuuta että muutosjono olisi päättyvä…

163. Redusoinnin strategiat
ž Sisältä-ulos (call by value)
— reduktion kohteeksi vasemmanpuoleisin
alimman tason ilmaus
— arvoparametri
ž Ulkoa-sisään (call by name)
— reduktion kohteeksi vasemmanpuoleisin
ylimmän tason ilmaus
— laiska evaluointi

164. Esimerkki: Sisältä ulos
(λx (λy z x) P) → (λx z[y/x] P)
= (λx z P)
→ z[x/P]
= z

165. Esimerkki: Ulkoa sisään
(λx (λy z x) P) → (λy z x)[x/P]
= (λy z P)
→ z[y/P]
= z

166. Laiska evaluointi
ž Lisp evaluoi ilmauksia “innokkaasti” eli
ulkoa sisään
ž Joissain funktionaalisissa kielissä (esim.
Haskell) ilmauksia käsitellään laiskasti eli
sisältä ulos
— molemmat tavat johtavat kuitenkin samaan
lopputulokseen
ž Laiska evaluointi mahdollistaa äärettömät
tietorakenteet
— tietorakenne on periaatteessa ääretön, mutta
sitä generoidaan (laiskasti) tarpeen mukaan

167. Lisp ja lambda-kalkyyli 1(2)
ž Lisp on lambda-kalkyylin laajennus
— ilmaukset voivat sisältää myös vakioita
(luvut, merkkijonot)
ž Tiettyihin funktiosymboleihin liittyy
erikoismerkitys ja erityinen
reduktiosääntö
— esim. (+ 1 2) tuottaa tulokseksi 3, vaikka
alkuperäinen ilmaus on jo redusoitu

168. Lisp ja lambda-kalkyyli 2(2)
ž λ-ilmaus λx1 λx2 … λxn M kirjoitetaan
muodossa
(lambda (x1 x2 ... xn) M)
ž λ-ilmaukselle voidaan antaa nimi, jota
voidaan käyttää ilmauksen asemasta
— esim. (lambda (x) (* x x x)) voidaan
nimetä kuutio

169. Esimerkki: Kuutio
(define kuutio
(lambda (x)
(* x x x)
)
)
; eo. tarkoittaa samaa kuin
(define (kuutio x)
(* x x x)
)

170. Esimerkki: Summaus
(define summa
(lambda (a b)
(+ a b)
)
)
(define monisumma
(lambda (x . y)
(apply + x y)
)
)

171. Listat
ž Atomi nil on lista (tyhjä lista)
ž Jos S ja T ovat atomeja, listakonstruktori
(S.T) yhdistää ne listaksi
ž Jos L1, L2,…, Ln ovat atomeja tai listoja,
niin (L1 L2 … Ln) on lista
— merkintätapa tarkoittaa samaa kuin
(L1.(L2.(…(Ln.nil)…)))
ž Kaikki lambda-ilmaukset voidaan
haluttaessa tulkita listoina
— mahdollistaa ohjelmien kohtelemisen tietona ja
tietojen kohtelemisen ohjelmina

172. Listojen käsittely
ž Listan pää: car
— esim. (car '(a b c d e)) = a
ž Listan häntä: cdr
— esim. (cdr '(a b c d e)) = (b c d e)
ž Lyhennysmerkintöjä
— (cXYr L) = (cXr (cYr L))
— (cXYZr L) = (cXr (cYr (cZr L)))
— esim. (car (cdr (cdr L))) voitaisiin
lyhentää (caddr L)

173. Esimerkki: listan alkioiden määrä
(define (alkioiden-lkm L)
(cond
((null? L) 0)
((null? (cdr L)) 1)
((null? (cddr L)) 2)
(else 'tosi-paljon)
)

174. Haskell: pääpiirteet
ž Laiska evaluointi
ž Staattinen tyypitys
ž Tyyppipäättely (type inference)

175. Esimerkkejä: Aritmetiikkaa
2 + 3
4 * 4 - 3
42 / 2
(32 * 23) + (34 / 3)
4 * (-2)

176. Boolen algebra ja yhtäsuuruus
ž Boolen operaatiot: True, False, not,
&&, ||
— esim: not (True && True)
ž Yhtäsuuruus == ja erisuuruus /=

177. Infix- ja prefix-funktiot
ž Infix-funktioissa operaattori on
operoitavien välissä
— esim. 2 * 3
ž Prefix-funktioissa operaattori
operoitavien edessä
— esim. succ 42, min 3 5
ž Prefix-funktio voidaan kirjoittaa infix-
muodossa lisäämällä takahipsut `
— esim. div 34 4, 34 `div` 4

178. Esimerkki: Funktioiden määrittely
tuplaaMinut x = x + x
tuplaaMeidat x y = x * 2 + y * 2
tuplaaMeidat' x y = tuplaaMinut x +
tuplaaMinut y
tuplaaPieniNumero x = if x > 100
then x
else x * 2

179. Listat 1(2)
ž Homogeenisia: kaikilla alkioilla sama tyyppi
— esim. numerot = [2, 4, 9, 11]
— esim. nimi = "B. Virtanen"
ž Listojen yhdistäminen ++
— esim. [1, 2, 3] ++ [4, 5, 6]
— esim. "Lennart" ++ "Nilkén"
ž Alkion liittäminen :
— esim. 'M' : "urikka"
— esim. 1 : [2, 3, 4]

180. Listat 2(2)
ž Alkion haku indeksillä !!
— esim. "Haskell" !! 3
ž Leksikografinen vertailu <, <=, =>, >
ž Arvoväli ..
— esim. [1..10], ['a'..'z']
— myös askellus, esim. [2, 4..10]

181. Listakoosteet (list
comprehensions)
ž Esim. [x * 2 | x <- [1..5]]
ž Predikaatit
— esim. [x * 2 | x <- [1..5], x * 2 > 5]
— esim. [ x | x <- [10..20], x /= 10, x /=
15, x /= 19]
— esim. [ x * y | x <- [2,3], y <- [3,4,5]]
ž Villikortti _
— esim. pituus xs = sum [1 | _ <- xs]

182. Tuplat
ž Voi sisältää eri tyyppejä
ž Tuplat on samanlaisia vain jos alkioiden
määrä ja tyypit vastaavat toisiaan
ž Esimerkkejä
— (1, 2)
— [(1, 2), (3, 4), (5, 6)]
— [("Fortran", 1954), ("Lisp", 1958),
("Algol", 1960)]
ž Funktioita
— fst(7, 3) palauttaa ensimmäisen alkion: 7
— snd(7, 3) palauttaa toisen alkion: 3
— zip [1..3] ['a'..'c'] yhdistää tuplat:
[(1, 'a'), (2, 'b'), (3, 'c')]

183. Tyypit ja tyyppiluokat
ž Yleisimmät tyypit: Int, Integer, Float,
Double, Bool, Char, Ordering
ž Esimerkkejä
— removeUpperCase :: [Char] -> [Char]
— lisaaKolme :: Int -> Int -> Int -> Int
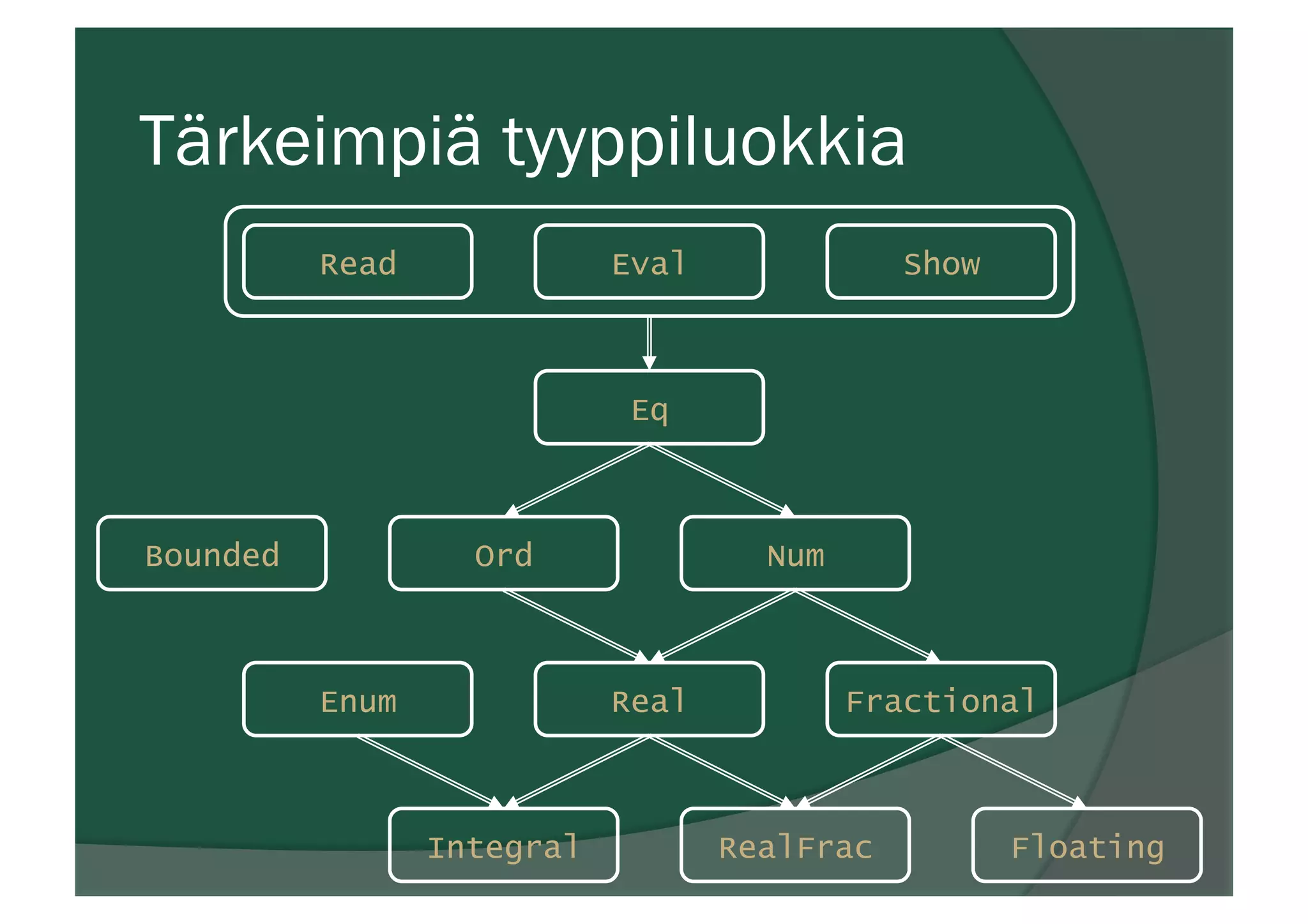
ž Tyyppiluokka ≈ tyyppien rajapinta
— mm. Eq, Ord, Show, Read, Bounded, Num,
Integral
— esim. yhtasuuri :: (Eq a) => a -> a ->
Bool

184. Tärkeimpiä tyyppiluokkia
Real FractionalEnum
Integral Floating
Bounded Ord Num
Eq
Read Eval Show
RealFrac

185. Funktiot: hahmon sovitus
tarkoitus :: (Integral a) => a -> String
tarkoitus 42 = "Oikein!"
tarkoitus x = "Väärin!"
kertoma :: (Integral a) => a -> a
kertoma 0 = 1
kertoma n = n * kertoma(n - 1)

186. Funktiot: vartijat
bmiArvio :: (RealFloat a) => a -> a -> String
bmiArvio paino pituus
| bmi <= laiha = "Olet alipainoinen."
| bmi <= normaali = "Olet normaalipainoinen."
| bmi <= lihava = "Olet ylipainoinen."
| otherwise = "Olet vaarallisen ylipainoinen."
where bmi = paino / pituus ^ 2
(laiha, normaali, lihava) = (18.5, 25.0, 30.0)

187. Esimerkki: listan maksimialkio
rekursiivisesti
maksimi :: (Ord a) => [a] -> a
maksimi [] = error "tyhjä lista"
maksimi [x] = x
maksimi (x:xs)
| x > maxHanta = x
| otherwise = maxHanta
where maxHanta = maksimi xs

188. Esimerkki: listan täyttö
tayta:: (Num i, Ord i) => i -> a -> [a]
tayta n x
| n <= 0 = []
| otherwhise = x:tayta (n-1) x

189. Esimerkki: alkioiden otto
ota :: (Num i, Ord i) => i -> [a] -> [a]
ota n _
| n <= 0 = []
ota _ [] = []
ota n (x:xs) = x : ota (n - 1) xs

190. Esimerkki: listan kääntäminen
kaanna :: [a] -> [a]
kaanna [] = []
kaanna (x:xs) = kaanna xs ++ [x]

191. Korkeamman asteen funktiot
ž Ottavat funktioita parametrinaan ja
palauttavat funktioita paluuarvoina
ž Haskelin funktiot ovat unaarisia (ts. niillä
voi olla vain yksi parametri)
ž Curry-muunnoksella (currying) saadaan
aikaan vaikutelma että funktiolla on
useampi parametri
— esim. funktionkutsu max 7 3 luo funktion, jolla
on yksi parametri ja joka palauttaa 7 jos
parametri on pienempi tai parametrin jos sen
suurempi kuin 7

192. Osittain sovelletut funktiot
ž Jos funktion kutsussa jätetään pois
parametreja, saadaan osittain sovellettu
funktio
— voidaan luoda lennossa uusia funktioita

193. Esimerkki: osittain sovellettu
funktio
kerroKolme :: (Num a) => a -> a -> a -> a
kerroKolme x y z = x * y * z
kerroKaksiKuudella :: (Num a) => a -> a -> a
kerroKaksiKuudella = kerroKolme 6
kerroKahdellatoista :: (Num a) => a -> a
kerroKahdellatoista = kerroKaksiKuudella 2

194. Esimerkki: funktio parametrina
sovellaKahdesti :: (a -> a) -> a -> a
sovellaKahdesti f x = f (f x)

195. Map
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs

196. Filter
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter p (x:xs)
| p x = x : filter p xs
| otherwise = filter p xs

197. Esimerkki: pikalajittelu
pikalajittele :: (Ord a) => [a] -> [a]
pikalajittele [] = []
pikalajittele (x:xs) =
pikalajittele pienet ++ [x] ++
pikalajittele suuret
where pienet = filter (< x) xs
suuret = filter (>= x) xs

198. Muita Haskelin piirteitä
ž Funktorit
ž Monadit

199. Syöttö- ja tulostus
main = do
putStrLn "Hei, mikä on nimesi?"
nimi <- getLine
putStrLn ("Hei " ++ nimi ++ ", hyvin menee!")
IO String String

201. Mitä on logiikkaohjelmointi?
ž Logiikkaohjelma koostuu joukosta logiikan
kaavoja
— logiikkaohjelmointi on näiden kaavojen
kirjoittamista
ž Ohjelman suoritus muodostuu ohjelman
loogisten seurausten automaatisesta
päättelystä
ž Ohjelmien merkitys (ideaalisti) on
tajuttavissa ilman mitään tietoa niiden
suoritustavasta
— kaavat ovat joko tosia tai epätosia riippumatta
siitä, miten itse todistus suoritetaan

202. Mitä ohjelmointi on?
Ohjelma = algoritmit + tietorakenteet
– Niklaus Wirth
Algoritmi = logiikka + kontrolli
– Robert Kowalski

203. Propositiologiikkaa
ž Propositio
— väittämä joka voi olla tosi tai epätosi
— suljettu lause
ž Symbolinen logiikka
— propositioiden esittäminen
— propositioiden välisten suhteiden (eli
relaatioiden) esittäminen
— uusien propositioiden päättely (eli
johtaminen) aikaisemmista tosista
propositioista

204. Propositiologiikan syntaksia
ž Propositiosymbolit
ž Loogiset konnektiivit: ⋀, ⋁, ¬, →, ↔
ž Päättelyoperaattorit: ⟹, ⟺
ž Propositiologiikan lakeja
— esim. vaihdantalait, liitäntälait, de Morganin
lait

205. Predikaattilogiikka
ž Formalismi selittävien eli deklaratiivisten
lauseiden matemaattiseen esittämiseen
— luonnollisen kielen ilmaus (eli väittämä) joka voi
olla joko tosi tai epätosi
— kohdistuvat jonkin tarkastelujoukon (eli
universumin) alkioihin ja niiden välisiin suhteisiin
(eli relaatioihin)
ž Siirros propositiologiikasta:
— propositioihin liitetään parametrit (eli predikaatti
voi olla avoin lause)
— kvanttorit: ∀, ∃

206. Avoimet ja suljetut lauseet
ž Muuttuja on sidottu jos se on kvanttorin
vaikutuspiirissä; muutoin se on vapaa
— esim. ∃X: X + Y = 1; X on sidottu, Y on
vapaa
ž Lause on suljettu, jos se ei sisällä
vapaita muuttujia; muutoin se on avoin
— suljetulla lauseella on totuusarvo
ž Avoimen lauseen totuusarvo riippuu
vapaille muuttujille annettavista arvoista

207. Looginen päättely
ž Johtopäätösten muodostamista muista
lauseista formaalien päättelysääntöjen
avulla
ž Päättelysääntöjä
— modus ponens (esim. X ⋀ (X → Y) ⟹ Y)
— kvanttorin eliminointi
(esim. oletetaan X ∈{ X1, X2, … Xn },
∀X: P(X) ↔ P(X1) ⋀ P(X2) ⋀ … ⋀ P(Xn)
∃X: P(X) ↔ P(X1) ⋁ P(X2) ⋁ … ⋁ P(Xn)

208. Automaattinen
teoreemantodistus
ž Predikaattilogiikan teoreemantodistus
liian vaikeaa
— on olemassa ongelmia joihin ei ole
algoritmista ratkaisua
ž Automaattinen teoreemantodistus
onnistuu vain syntaksiltaan rajoitetuille
kaavoille
— definiitti klausuuli
— voidaan soveltaa yksinkertaista ja tehokasta
SLD-päättelysääntöä

209. Definiitti klausuuli
ž Ilmaistaan kahdentyyppistä tietoa:
— fakta: jokin relaatio on (varauksetta)
voimassa tiettyjen objektien välillä
— sääntö: relaatio on voimassa kunhan jotkin
muut relaatiot ovat
ž Klausuulin syntaktinen muoto (eli Hornin
klausuuli)
H ← B1 ⋀ … ⋀ Bn (n ≥ 0)
— jos n = 0, kyseessä on fakta, muutoin sääntö

210. Definiitti logiikkaohjelma
ž Äärellinen joukko definiittejä klausuuleita
ž Tehtävien johtopäätösten joukko on
yleensä ääretön
ž Esittämällä koneelle yksittäinen kysely
(eli maali) selvitetään onko se ohjelman
seuraus vai ei
— kyselyn syntaktinen muoto: ← B1 ⋀ … ⋀ Bm

211. Prolog
ž Sopii ohjelmiin joissa käytetään symbolista
tai ei-numeerista laskentaa
— esim. tekoälysovellukset
ž Koostuu joukosta sääntöjä ja faktoja
— ohjelma ajetaan esittämällä kysely ja toteamalla
voidaanko se perustella niiden perusteella
ž Lauseet muodostetaan seuraavista
termeistä
— vakio (kokonaisluku tai atomi)
— muuttuja
— funktori

212. Prolog-lauseet
ž Faktat
— lauseita joiden oletetaan olevan tosia
— käyttäjän määräämä merkitys
ž Säännöt
— vastaavat matematiikan teoreemoja, joista
voidaan vetää johtopäätöksiä jos tietyt ehdot
toteutuvat
ž Kyselyt
— tavoitteena selvittää onko annettu kysely tosi vai
ei (eli “Yes” tai “No”)
— järjestelmä antaa ne muuttujien instanssit joilla
lause on tosi

213. Aritmetiikkaa
ž Samastaminen: =
— esim. X = 3 + 4, muuttuja X samastetaan
termiin 3 + 4
ž Lausekkeen evaluointi: is
— esim. X is 3 + 4, muuttujaan X sijoitetaan
termi 7

214. Yksinkertaiset faktat
ž Faktat muodostuvat tietystä asiasta tai
asioiden välisestä relaatiosta
ž Esimerkki:
aurinkoista.
minkä jälkeen tehdään Prologille kysely
?- aurinkoista.
Yes
ž Syntaksi: alkaa pienellä kirjaimella ja
päättyy pisteeseen

215. Relaatiofaktat
ž Faktaan voi liittyä yksi tai useampia
argumentteja
ž Esimerkki:
tykkaa(jussi, maria).
— huom. relaatiolla ei ole suuntaa (siis Jussi
voi tykätä Mariasta tai päinvastoin)

216. Esimerkki: relaatiofaktoja 1
syo(risto, omena).
syo(risto, kyljys).
syo(tommi, banaani).
syo(jussi, banaani).
syo(jussi, kiwi).
?- syo(risto, omena).
Yes
?- syo(jussi, banaani).
Yes
?- syo(mika, banaani).
No
?- syo(risto, banaani).
No

217. Esimerkki: relaatiofaktoja 2
ika(jussi, 23).
ika(amalia, 14).
ika(ylermi, 47).
ika(iikka, 5).
ika(tuomas, 35).
?- ika(iikka, 5).
Yes
?- amalia(14).
No
?- ika(iikka, viisi).
No

218. Muuttujat ja samastaminen
ž Muuttujat alkavat isolla kirjaimella
ž Esim. oletetaan että meillä on fakta
syo(risto, omena).
kuinka kysytään mitä Risto syö?
?- syo(risto, Mita).
Mita=omena
Yes
— muuttuja Mita samastuu arvoon omena

219. Esimerkki: muuttujat 1
tykkaa(jussi, maria).
tykkaa(risto, askartelu).
?- tykkaa(jussi, Kuka).
Kuka=maria
Yes
?- tykkaa(arska, Kuka).
No
?- tykkaa(risto, Kuka).
Kuka=askartelu
Yes

220. Esimerkki: muuttujat 2
levy(1, pink_floyd, meddle, echoes).
levy(2, led_zeppelin, physical_graffiti, trampled_under_foot).
levy(3, the_beatles, abbey_road, something).
levy(4, genesis, foxtrot, suppers_ready).
levy(5, rolling_stones, sticky_fingers, brown_sugar).
?- levy(3, Artisti, Albumi, Lemppari).
Artisti=the_beatles
Albumi=abbey_road
Lemppari=something
Yes
?- levy(2, led_zeppelin, physical_graffiti, Lemppari).
Lemppari=trampled_under_foot
Yes

221. Säännöt
ž Mahdollistavat ehdolliset lauseet
universumista
— jokaisella säännöllä on monta variaatiota joita
sanotaan klausuuleiksi
— klausuulit antavat erilaisia mahdollisuuksia
päättelyyn
ž Esim. “Kaikki ihmiset ovat kuolevaisia”
kuolevainen(X) :- ihminen(X).
— deklaratiivinen tulkinta: Annetulle X:lle, X on
kuolevainen, jos X on ihminen
— proseduraalinen tulkinta: Todistaaksesi maali X
on kuolevainen, todista alimaali X on ihminen

222. Esimerkki: säännöt 1
kuolevainen(X) :- ihminen(X).
ihminen(sokrates).
?- kuolevainen(sokrates).
Yes
?- kuolevainen(P).
P=sokrates
Yes

223. Esimerkki: säännöt 2
hauskaa(X) :- punainen(X), auto(X).
hauskaa(X) :- sininen(X), mopo(X).
auto(lada).
auto(mosse).
mopo(pappa_tunturi).
punainen(lada).
punainen(mosse).
sininen(pappa_tunturi).
?- hauskaa(pappa_tunturi).
Yes
?- hauskaa(Mika).
Mika=lada;
Mika=mosse;
Mika=pappa_tunturi;
No

224. Esimerkki: peräytys
(backtracking)
pitaa_juhlat(X) :- syntymapaiva(X), onnellinen(X).
syntymapaiva(tommi).
syntymapaiva(risto).
syntymapaiva(henna).
onnellinen(maria).
onnellinen(jaana).
onnellinen(henna).
?- pitaa_juhlat(Kuka).
Kuka=henna
Yes

225. Esimerkki: rekursio 1
matkalla(rooma).
matkalla(Paikka) :-
siirry(Paikka, Kulkuneuvo, UusiPaikka),
matkalla(UusiPaikka).
siirry(koti, taksi, tku).
siirry(tku, lentokone, hel).
siirry(hel, lentokone, rooma).
?- matkalla(koti).
Yes

226. Esimerkki: rekursio
vanhempi(jussi, paavo).
vanhempi(paavo, tuomas).
vanhempi(tuomas, maria).
esivanhempi(X, Y) :- vanhempi(X, Y).
esivanhempi(X, Y) :- vanhempi(X, Z),
esivanhempi(Z, Y).
?- esivanhempi(jussi, tuomas)
Yes

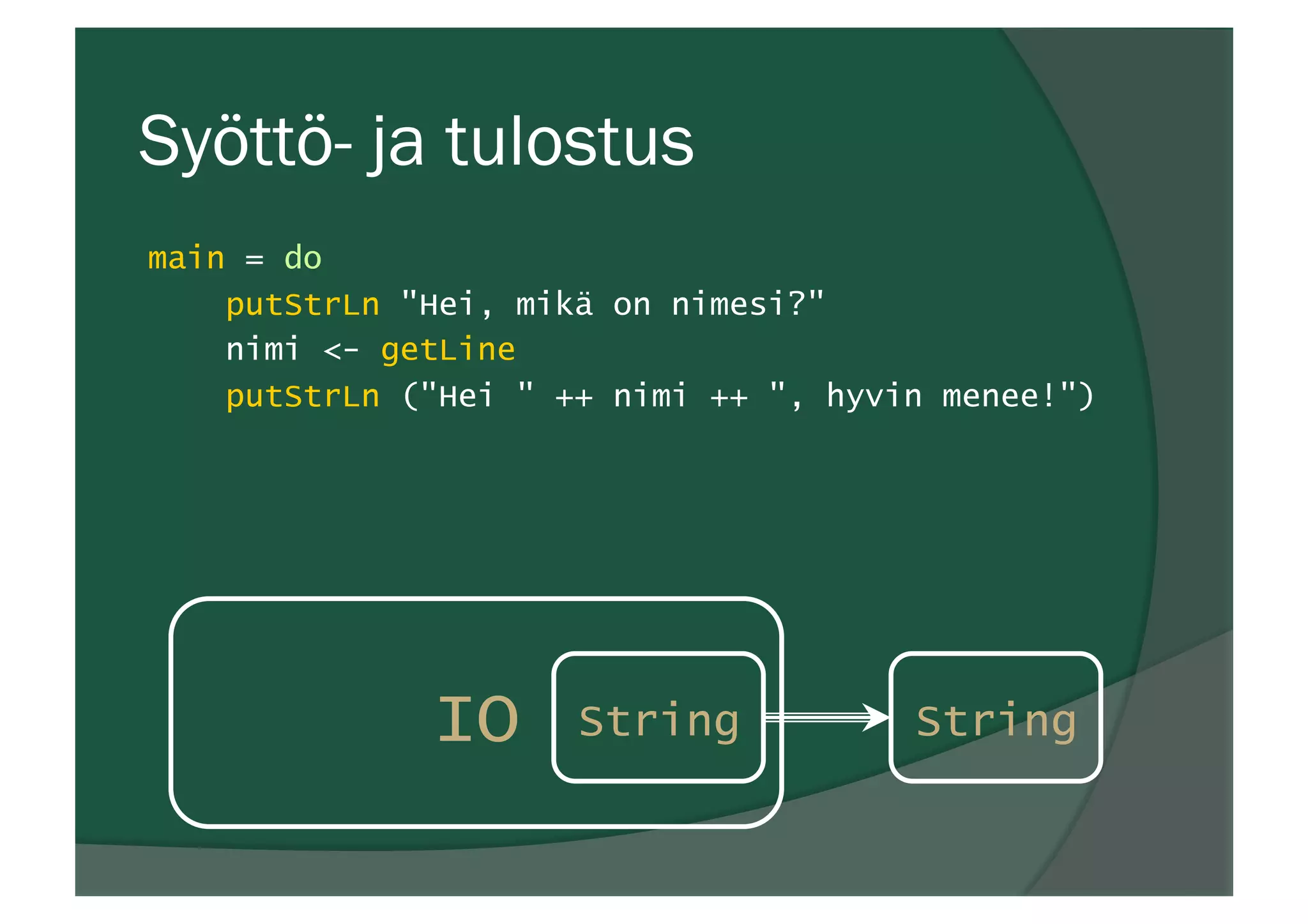
227. Listat
ž Syntaksi: luetellaan alkiot hakasuluissa
pilkuilla erotettuina
— esim. [a, risto, Muuttuja, omena]
— tyhjä lista: []
ž Pään ja hännän erottaminen: |
— esim. [yksi, kaksi, kolme] = [A|B],
missä A = yksi ja B = [kaksi, kolme]

228. Esimerkki: listat
p([Paa|Hanta], Paa, Hanta).
?- p([a, b, c], X, Y).
X=a
Y=[b, c]
Yes
?- p([a], X, Y).
X=a
Y= []
Yes
?- p([], X, Y).
No

229. Esimerkki: listasta haku
on(Alkio, [Alkio|Loput]).
on(Alkio, [JataPaaValiin|Hanta]) :- on(Alkio, Hanta).
?- on(omena, [kiwi, kurkku, omena, banaani]).
Yes

230. Esimerkki: listan rakentaminen
yhdista([], Lista, Lista).
yhdista([Paa|Hanta], Lista2, [Paa|Tulos]) :-
yhdista(Hanta, Lista2, Tulos).
?- yhdista([a, b, c], [yy, kaa, koo], Tulos).
Tulos = [a, b, c, yy, kaa, koo]
Yes

231. Esimerkki: listan suodatus
suodata([], []).
suodata([X|Hanta], [X|Tulos]) :-
X > 6, suodata(Hanta, Tulos).
suodata([HeitaPois|Hanta], Tulos) :-
suodata(Hanta, Tulos).
?- suodata([1, 12, 3, 14, 5, 8], Tulos).
Tulos=[12, 14, 8]
Yes

232. sisaan!
kaivo!
limbo!
keiju!
rosvot!
ulos!
ruokaa!
aarre!
peikot!

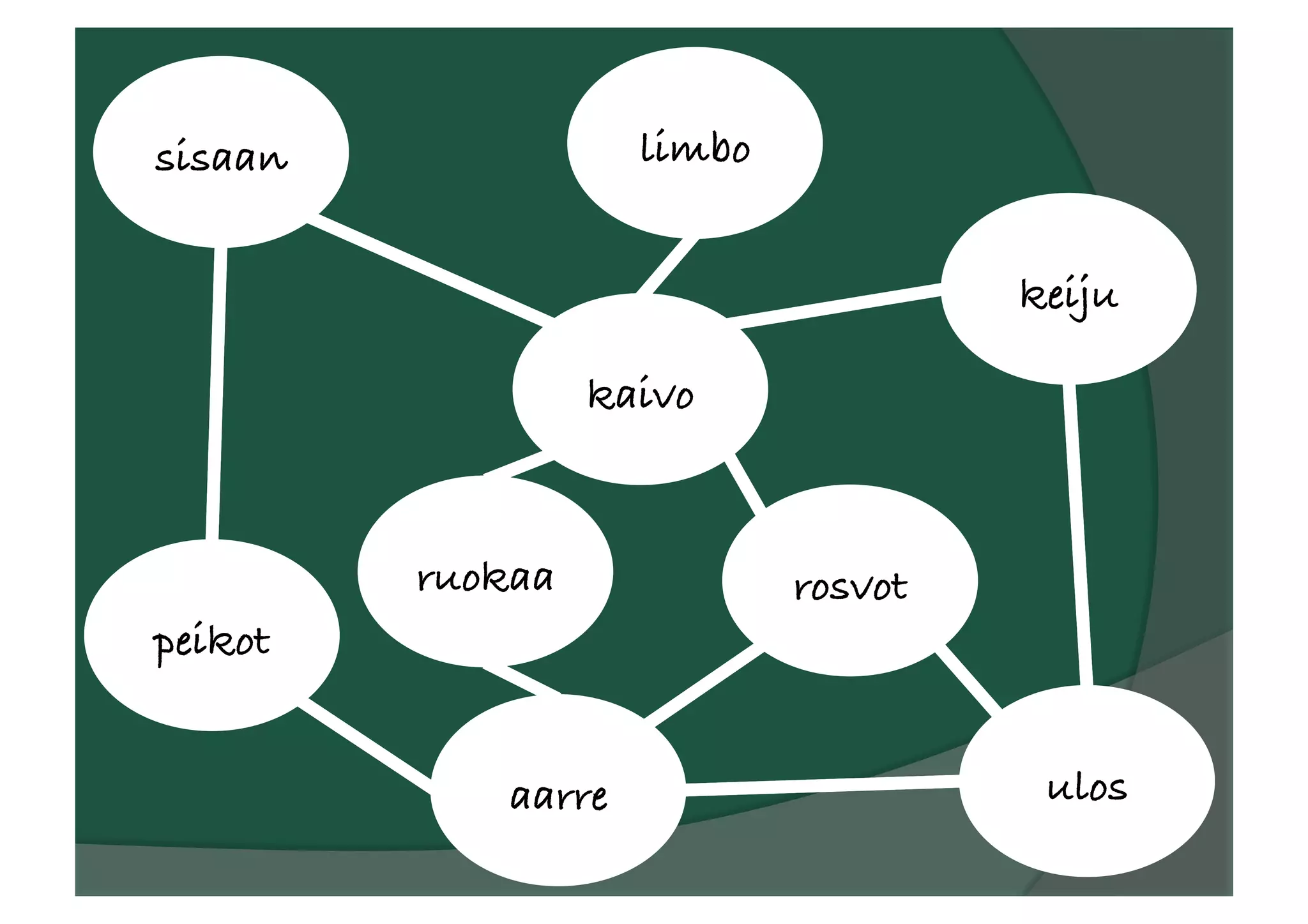
233. Esimerkki: Labyrintti 1(3)
naapurit(sisaan, peikot). naapurit(sisaan,
kaivo).
naapurit(kaivo, limbo). naapurit(kaivo, ruokaa).
naapurit(kaivo, rosvot). naapurit(kaivo, keiju).
naapurit(rosvot, aarre).
naapurit(rosvot, ulos).
naapurit(ruokaa, aarre). naapurit(peikot, aarre).
naapurit(keiju, ulos). naapurit(aarre, ulos).
valta([peikot, rosvot]).
kulje(Taalta, Tuonne) :-
valta(Vaarat),
polku(Taalta, Tuonne, Vaarat, [Taalta]).

234. Esimerkki: Labyrintti 2(3)
polku(Tama, Tama, Vaarat, Vana) :-
jasen(aarre, Vana),
kaanteiskirjoita(Vana).
polku(Mista, Mihin, Vaarat, Vana) :-
(naapuri(Mista, Etappi); naapuri(Etappi, Mihin)),
not jasen(Etappi, Vaarat),
not jasen(Etappi, Vana),
polku(Etappi, Mihin, Vaarat, [Etappi|Vana]).
kaanteiskirjoita([]).
kaanteiskirjoita([Paa|Hanta]) :-
kaanteiskirjoita(Hanta), nl, write(Head).
jasen(X, [X|_]).
jasen(X, [_|Y]) :- jasen(X, Y).

235. Esimerkki: Labyrintti 3(3)
?- kulje(sisaan, ulos).
sisaan
kaivo
ruokaa
aarre
ulos
Yes

236. Prologin puutteita
ž Resoluutiojärjestyksen kontrollointi
— järjestys vaikuttaa tehokkuuteen
— ikuiset silmukat mahdollisia
ž Oletus suljetusta maailmasta
— tavoite voidaan osoittaa todeksi muttei
epätodeksi
ž Negaatio-ongelma
ž Luontaiset rajoitukset
— ei tarvitse kuvata, miten jokin tehtävä
suoritetaan

238. Käsiteltävät aiheet
ž Skriptiohjelmointi
ž Prototyyppipohjaiset kielet
ž Kompositiopohjainen ohjelmointi
(concatenative programming)
ž Tietovuo-ohjelmointi (dataflow
programming)
ž Visuaalinen ohjelmointi
ž Esoteeriset ohjelmointikielet

239. Skriptiohjelmointi
ž Olemassa olevien
ohjelmistokomponenttien yhdistely
ž Joustavuus: tyypittömyys tai
dynaaminen tyypitys
ž Tulkattavuus
ž Upottaminen muihin tiedostoihin (esim.
HTML-dokumentteihin)
ž Refleksiivisyys

240. Historiaa
ž Kaksi esivanhempaa
— komentotulkit (eli kuoret, shells)
○ JCL, MS-DOSin command, Unixin sh ja csh
— tekstinkäsittelyn ja raportingeneroinnin työkalut
○ IBM:n RPG, Unixin sed ja awk
ž Yleiskielet
— IBM:n Rexx
— Perl
— muita: Tcl, Python, Ruby, VBScript, AppleScript
ž Skriptikielet yleistyivät web-sovellusten myötä
— PHP
— JSP, Ruby on Rails, VBScript
— JavaScript

241. Vertailua
ž Perinteinen ohjelmointikieli
— tarkoitettu itsenäisten sovellusten
rakentamiseen
○ syöte, tiedon käsittely, tulostus
ž Skriptikieli
— tarkoitettu useiden sovellusten koordinointiin
○ testit ja ehdot, silmukat, muuttujat ja tyypit,
aliohjelmat ja abstraktiot
— toimii sovellusten ulkopuolella (“liimaa” ne
yhteen)

242. “Scripting languages assume that a
collection of useful components
already exist in other languages.
They are intended not for writing
applications from scratch but rather
for combining their components.”
– John Ousterhout

243. Yhteisiä piirteitä 1(3)
ž Sekä eräajo- että vuorovaikutteinen
käyttö
— harvoilla kielillä on kääntäjä (poikkeus Perl)
ž Ilmausten ekonomisuus
— kaiken ylimääräisen minimointi: välimerkit,
lyhyet avainsanat
ž Määrittelyjen puuttuminen;
yksinkertaiset näkyvyyssäännöt
— oletuksena kaikki globaalia (esim. Perl) tai
lokaalia (esim. PHP ja Tcl)

244. Yhteisiä piirteitä 2(3)
ž Joustava dynaaminen tyypitys
— tyyppi tarkistetaan joko ennen käyttöä (esim.
PHP, Python) tai muuttuja tulkitaan eri tavalla eri
kontekstissa (esim. Rexx, Perl, Tcl)
○ esim. Perl-ohjelma
$a = "4";
print $a . 3 . "n";
print $a + 3 . "n";
tulostaa 43 ja 7
ž Helppo pääsy alla olevan järjestelmän
palveluihin

245. Yhteisiä piirteitä 3(3)
ž Kehittyneet operaatiot
hahmonsovitukseen ja merkkijonojen
käsittelyyn
— pohjautuvat usein säännöllisiin ilmauksiin
(regular expression)
ž Korkean tason tietotyypit
— esim. joukot, listat, tuplat, kuvaukset
— roskien keruu

246. Prototyyppipohjainen ohjelmointi
ž Tukee monia olio-ohjelmoinnin piirteitä
— kapselointi
— jäsenmuuttujat ja metodit
ž Ei luokkamäärityksiä
— oliot luodaan joko tyhjästä tai kloonaamalla
olemassa oleva olio
ž Periytyminen: kloonataan toinen olio
(joka on siis uuden olion prototyyppi)
ž Kieliä: JavaScript, Lua, Self, Io

247. Miksei periytymistä vaan
prototyyppejä?
ž Oliokielissä ohjelmoija keskittyy usein ensin
luokkien taksonomiaan ja niiden välisiin
suhteisiin
ž Prototyyppipohjaisisssa kielissä
— ohjelmoija keskittyy ensin muutamasta oliosta
muodostuvan joukon käyttäytymiseen
— myöhemmin olioita luokitellaan arkkityyppisiksi
olioiksi
— prototyyppejä ohjataan muokattavaksi ajoaikana (vrt.
oliokielten luokkien käännösaikainen määrittely)
ž Lähes kaikki prototyyppipohjaiset kielet ovat
tulkittavia ja dynaamisesti tyypitettyjä

248. Olion luonti
ž Luokkapohjaisissa kielisssä olio luodaan
konstruktorin avulla
— instanssi saa kaikki luokassa määritellyt piirteet
ž Prototyyppipohjaisissa kielissä ei ole
luokkia vaan olion periytyvät suoraan
toisista olioista (joka on siis uuden olion
prototyyppi)
ž Konstruointi
— olio luodaan tyhjästä (ex nihilo)
— olio luodaan kloonaamalla olemassa oleva olio
ž Konstruoinnin jälkeen oliota voidaan
muuntaa halutulla tavalla

249. Kritiikkiä
ž Oikeellisuus
— luokat ovat analogisia tyyppien kanssa, joten
ne tarjoavat olioille ja niiden käyttäjille takeet
siitä että oliot käyttäytyvät tietyllä tavalla
ž Turvallisuus
ž Ennustettavuus
ž Tehokkuus
— luokkia käytettäessä kääntäjä voi tehdä
enemmän optimointeja kuin prototyyppien
kanssa

250. Kompositiopohjainen
(concatenative) ohjelmointi
ž Käyttää funktion kompositiota
(composition) funktion soveltamisen
(application) sijaan
ž Funktio
— saa mielivaltaisen määrän syötteitä
— käyttää niistä vain päällimmäisiä
— palauttaa käyttämättömät syötteet, joita seuraa
varsinainen tulos
ž Siis kyseessähän on… pino!
ž Ohjelmat ovat yksinkertaisia ja triviaaleja
suorittaa tehokkaasti

251. Esimerkki: 2 3 × 4 5 × +
Funktio Tulos
()
2 (2)
3 (2, 3)
× (6)
4 (6, 4)
5 (6, 4, 5)
× (6, 20)
+ (26)

252. Kompositiopohjaisia kieliä
ž Java Virtual Machine
— tavukoodi
ž CPython-tavukoodi
— käyttäjiä mm. BitTorrent, Dropbox ja YouTube
ž PostScript-kuvauskieli
ž Forth-kieli
— sulautetut järjestelmät
— Open Firmware, OpenBoot
— avaruussovellukset

253. Tietovuo-ohjelmointi (dataflow
programming)
ž Mallintaa ohjelman suunnattuna graafina,
joka kuvaa kuinka tieto virtaa operaatioiden
välillä
ž Pyrkii määrittämään, kuinka asiat liittyvät
toisiinsa
— vrt. imperatiivinen ohjelmointi määrittelee kuinka
asiat tapahtuvat (ts. tietovuo on toissijasta
kontrollivuon rinnalla)
ž Tietovuo-ohjelma on sarja (mahdollisesti
toisiinsa liittyviä) yhteyksiä
— operaatiot ovat toissijaisia
ž Historiaa: Unixin putket

254. Tilan käsite
ž Normaalisti tietokone ei tiedä että jokin
informaation pala sisältää tilan
— sen sijaan: informaation pala on väliaikaista ja
voidaan pian hylätä
ž Ongelma: tilatietoa voidaan joutua
jakamaan usean prosessorin kesken esim.
rinnakkaislaskennassa
— ohjelmoijan täytyy laittaa lisäkoodia kertomaan
mikä tieto on tärkeää
○ lisää suoritusaikaa, vaikeaa debugata, rumaa
ž Tietovuo-ohjelmoinnissa tilan käsite ei
häviä

255. Tietovuo-ohjelma
ž Ohjelmat alkavat syötteestä, joka kuvaa
kuinka tietoa käytetään ja muunnetaan
— tieto on nyt eksplisiittistä (voidaan kuvata
jopa graafisesti)
ž Operaatiot ovat “mustia laatikkoja”
— vrt. sarja työläisiä asennuslinjalla
— rinnakkaistuvaa

256. Visuaalinen ohjelmointi
ž Ohjelmia luodaan käsittelemällä
elementtejä graafisesti
— ikoni-pohjaiset
— lomakepohjaiset
— diagrammipohjaiset
ž Nykypyrkimyksenä visuaalisen ja
tietovuo-ohjelmoinnin yhdistäminen

257. Esimerkki: Scratch

258. Esoteeriset ohjelmointikielet
ž Tarkoituksena on poistaa tai korvata
konventionaalisia kielten piirteitä säilyttäen
Turing-täydellisyys
— ohjelmointikielten rajojen tutkiminen
— ohjelmointikielten parodisointi
ž Esimerkkejä
— INTERCAL
— FALSE
— brainfuck
— Befunge
— Piet
— Shakespeare
— Whitespace

259. INTERCAL: Hello, world
DO ,1 <- #13
PLEASE DO ,1 SUB #1 <- #238
DO ,1 SUB #2 <- #108
DO ,1 SUB #3 <- #112
DO ,1 SUB #4 <- #0
DO ,1 SUB #5 <- #64
DO ,1 SUB #6 <- #194
DO ,1 SUB #7 <- #48
PLEASE DO ,1 SUB #8 <- #22
DO ,1 SUB #9 <- #248
DO ,1 SUB #10 <- #168
DO ,1 SUB #11 <- #24
DO ,1 SUB #12 <- #16
DO ,1 SUB #13 <- #162
PLEASE READ OUT ,1
PLEASE GIVE UP

260. Brainfuck-kielen 8 komentoa
Komento Toiminto
> Lisää osoittimen osoitteeseen yksi
< Vähennä osoittimen osoitteesta yksi
+ Lisää osoittimen osoittamaa tavua yhdellä
- Vähennä osoittimen osoittamaan tavua yhdellä
. Tulosta osoittimen osoittama tavu ASCII-merkkinä
, Lue syötteestä arvo osoittimen osoittamaan tavuun
[ Jos osoittimen osoittama tavu on nolla, hyppää
eteenpäin vastaavaan ]-merkkiin
] Jos osoittimen osoittama tavu ei ole nolla, hyppää
taaksepäin vastaavaan [-merkkiin

261. Esimerkki: Hello, World!
++++++++++[>+++++++>+
+++++++++>+++>+<<<<-]
>++.>+.+++++++..+++.>
++.<<+++++++++++++++.
>.+++.------.--------
.>+.>.

262. Esimerkki: Hello, world!
(kommentoituna)
+++++ +++++ initialize counter (cell #0) to 10
[ use loop to set the next four cells to 70/100/30/10
> +++++ ++ add 7 to cell #1
> +++++ +++++ add 10 to cell #2
> +++ add 3 to cell #3
> + add 1 to cell #4
<<<< - decrement counter (cell #0)
]
> ++ . print 'H'
> + . print 'e'
+++++ ++ . print 'l'
. print 'l'
+++ . print 'o'
> ++ . print ' '
<< +++++ +++++ +++++ . print 'W'
> . print 'o'
+++ . print 'r'
----- - . print 'l'
----- --- . print 'd'
> + . print '!'
> . print 'n'

263. Befunge: Hello, World!
> v
v ,,,,"Hello,"<
>48*, v
v,,,,,,"World!"<
>25*,@

264. Piet: Hello World

266. Kurssin arvostelu
ž Arvostelu
perustuu 100
pisteeseen
ž Pistejako
— tentti: 60 pistettä
— demonstraatiot:
20 pistettä
— harjoitustyö: 20
pistettä
ž Hyväksytty
kurssi vaatii
yhteensä 45
pistettä
ž Arvosanajako
— [45,55) ⇒ 1
— [55, 65) ⇒ 2
— [65, 75) ⇒ 3
— [75, 85) ⇒ 4
— [85, 100] ⇒ 5

267. Harjoitustyö
ž Tehdään 4. periodissa
— valitse annetuista vaihtoehdoista yksi ohjelmointikieli
ja yksi tehtävä
— laadi ratkaisustasi 5–10 sivuinen raportti
— palauta moodlen kautta 5.5.2014 klo 14:00
mennessä
ž Arvostelu
— hylätty (0 pistettä)
— välttävä (5 pistettä)
— tyydyttävä (10 pistettä)
— hyvä (15 pistettä)
— kiitettävä (20 pistettä)
ž Ohjeet moodle-sivulla (ks. bit.ly/okp2014)

268. Tentit
ž Sähköinen tentti
— avautuu 5.5.2014
— sulkeutuu 30.9.2014
ž Tentin voi suorittaa enintään kolme (3)
kertaa
ž Lisäohjeita ja ajanvaraus:
https://tenttis.utu.fi

269. Miksi tutustua erilaisiin
ohjelmointikieliin?
ž Ajatusten esitttämiskyky laajenee
ž Riittävät taustatiedot sopivan
ohjelmointikielen valintaan
ž Kyky omaksua uusia ohjelmointikieliä
ž Kielen toteutuksen merkityksen
ymmärtäminen
ž Kyky seurata, ymmärtää ja arvioida
ohjelmointikielten kehitystä

270. Kaksi kirjasuositusta
Bruce A. Tate: Seven Languages in
Seven Weeks. Pragmatic Bookshelf,
2010.
Federico Biancuzzi & Shane Warden
(toim.): Masterminds of Programming.
O’Reilly Media, 2009.