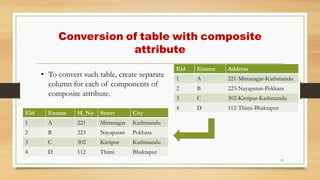
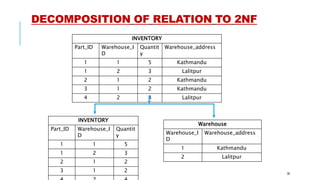
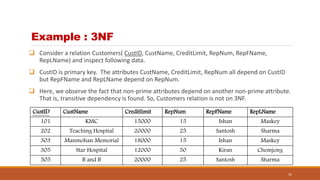
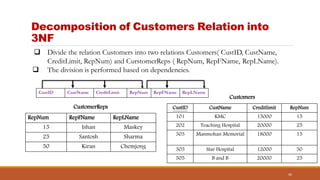
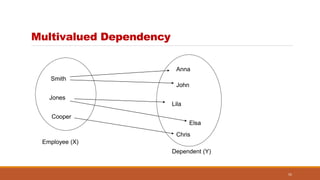
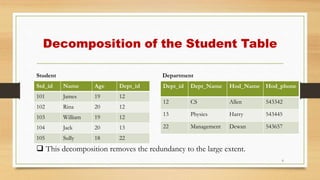
The document discusses database normalization and functional dependencies. It defines normalization as imposing rules on database tables to eliminate anomalies during data manipulation. Functional dependency is defined as a relationship where a set of attributes determines another. The properties of functional dependencies - reflexive, augmentation, transitive, union, and decomposition - are explained and examples are given. Normalization and understanding functional dependencies helps design high quality databases without redundancies or anomalies.

1. ADBMS
By: Dabbal S. Mahara
2018

2.  The goal of relational database design is to generate a set of relation schemas
that allows us to store information without unnecessary redundancy, yet also
allowing us to retrieve information easily.
 One approach is to design schemas that are in an appropriate normal form.
 Normalization is carried out in practice so that the resulting designs are of high
quality and meet the desirable properties.
 Data normalization is a set of rules and techniques concerned with:
• Identifying relationships among attributes.
• Combining attributes to form relations.
• Combining relations to form a database.
2
Introduction

3. What is data redundancy?
 Data redundancy is the repetition of same data in the table.
 It is the major problem in the database.
 Example: Let us consider the table student.
 In this table the information related to department of study for students is
repeated. This is called data redundancy.
 Normalization decomposes the relation into smaller relations so that
redundancy can be minimized.
3
Std_id Name Age Dpt_id Dpt_name HOD_name HOD_phone
101 James 19 12 CS Allen 543342
102 Rina 20 12 CS Allen 543342
103 William 19 12 CS Allen 543342
104 Jack 20 13 Physics Harry 543445
105 Sully 18 22 Management Dewan 543657
Student

4. Database Anomalies
 Another advantage of normalization process is that it eliminates the database
anomalies.
 The database anomalies are the problems during the DML operations in the
database.
 There are three types of anomalies:
 Insert Anomaly
 Delete Anomaly
 Update Anomaly
 Insert Anomaly:
 It occurs when we want to insert data into the relation.
 For example: if we want to insert department information in above table
student, we have to keep all the information related student null. That may
not be possible if std_id is a primary key.
 Similarly we want to insert student information, there should be department
information. 4

5. Database Anomalies
 Delete Anomaly:
 This is a problem due to the deletion of records in the relation.
 For example: if we deleted a record from student table, the corresponding
information of department is also deleted and we lose the department
information.
 When we delete last record in the relation, we will not have department
information at all. What if we want to know who is HOD of Management
Department department at this time.
 Update Anomaly:
 This is problem when we perform update operation to any field.
 For example: if HOD of CS department changes, new HOD is ‘Peter’, this single
piece of change in data results to a set of changes to relation. We have to change
each record related to CS department.
 If we missed change in some records, the data inconsistency may occur.
This is called update anomaly.
5

6. Decomposition of the Student Table
Std_id Name Age Dept_id
101 James 19 12
102 Rina 20 12
103 William 19 12
104 Jack 20 13
105 Sully 18 22
6
Dept_id Dept_Name Hod_Name Hod_phone
12 CS Allen 543342
13 Physics Harry 543445
22 Management Dewan 543657
Student Department
 This decomposition removes the redundancy to the large extent.

7. Normalization
 Normalization is the solution for database anomalies.
 Normalization is nothing but imposing some systematic rules on the tables so that the tables
do not have above design problems or anomalies.
 There are four normal forms usually which are popular, called 1NF, 2NF, 3NF and BCNF.
 There are other normal forms as well called 4NF, 5NF and DKNF - a lot of database
designers often find it unnecessary to go beyond 3rd Normal Form.
 This does not mean that those higher forms are unimportant, just that the circumstances for
which they were designed often do not exist within a particular database.
 However, all database designers should be aware of all the forms of normalization so that they
may be in a better position to detect when a particular rule of normalization is broken and
then decide if it is necessary to take appropriate action. 7

8. Functional Dependency
• Functional dependency is a property of the semantics of the attributes.
• Let X and Y be subsets of attributes of a relation R. The Functional Dependency
(FD), denoted as X -> Y, read as X functionally determines Y or Y functionally depends on
X, is defined as an association that each value of X determines a unique value for Y.
• More formally, for any two tuples t1 and t2 in the relation R: If t1[X] = t2[X], then
t1[Y] = t2[Y]. Informally, if X values agree in any two tuples of R, then Y values
must agree for corresponding tuples.
• The database designers use their understanding of the semantics of the attributes of
R to specify the functional dependencies on data.
• The main use of functional dependencies is to describe further a relation schema R
by specifying constraints on its attributes that must hold at all times. 8

9. Functional Dependency
 If you know the value of X, you can determine the
value of Y.
If you have X = a and Y= 1, then each time X = a,
Y must have value of 1 as shown in relation R.
 FDs are constraints that are derived from the
meaning and interrelationships of the data attributes.
 Functional dependencies (FDs) are used to specify
formal measures of the "goodness" of relational
designs.
 FDs are used to determine keys and consequently
to define normal forms for relations.
9
Relation R
X Y
a 1
b 2
a 1
c 3
a 1

10. Functional Dependency
 It is similar to mathematical notion of functions f : X → Y , where X, Y are
attributes of some table R. That is, the value of X uniquely defines the value of Y.
 This functional dependency does not mean that if you have value of X, you can
compute value of Y. Instead it means if you have value of X, you can search the value
of Y from the given table.
 For example: if we have a relation Employees(Ssn, Ename, email, salary, dno) and Ssn
is primary key, then Ssn can determine Ename, email, salary and dno of each
employee. That is, if we are given Ssn, we can determine all other attributes of this
employee.
 So, Ssn → Ename, Ssn → email, Ssn → salary, Ssn → dno.
 But, this may not be the case if we are given ‘Ename’ and asked to find corresponding
attributes.
10

11. Example : Functional Dependency
• Let us consider a company XYZ with following table, Car with fields employee id ‘eid’, car name ‘cname’,
parking area ‘parea’. Every employee has exactly one car and car name should decide the parking area. These
are the rules imposed on the table.
• There are three parking areas : A for AC
B for Non-AC but spacious and C for congested
and highly risky to park.
• There is a rule that Nano car should go to parking
area C, BMW should go to area B and Bench should
go to area A.
• This means car name decides the parking area
i.e. Cname -> Parea.
• If car name is Nano, the corresponding entry for parking area should be same i.e. ‘C’.
• That is, there is a functional dependency between Cname and Parea.
11
Eid Cname Parea
1 Nano C
2 Bench A
3 BMW B
4 Nano C

12. Example : Functional
Dependency
 To find functional relationship between the attributes, we should know about properties of the data.
 For example, consider the relation: student ( Sid, Sname, Fname, Marks)
 Sid can determine student name if we have Sid as a unique.
That is, Sid -> Sname is perfectly valid because if two tuples have same value for Sid
corresponding Sname cannot have different values.
 Notice that if Sid is given, we determine the name of student. But, Sname -> Marks is not true.
because there may be multiple students with same Sname but not necessarily with same Marks.
12
Sid Sname Fname Marks
1 Raju Rabin 58
2 Manju Manoj 48
3 Semon Saroj 59
4 Raju Prakash 47

13. Exercise
• Test which of the following is functional dependency.
i. A -> B
ii. B -> C
iii. AB -> C
iv. A -> C
v. C -> B
Note: if tuples in A agree, the two tuples must agree in B to be FD A->B
i.e. if t1[A] = t2[A] then t1[B] = t2[B]. 13
A B C
1 2 3
1 2 3
2 3 4
2 4 4
3 5 7

14. Properties of Functional Dependency
• The properties of FD are used to infer logically implied functional dependencies.
• By applying these rules closure of some set F of FD ( F+ ) can be computed.
• Every functional dependency satisfies these blind rules. They are universal rules.
1. Reflexive Property: If X ⊇ Y then X → Y.
2. Augmentation Property: If W → Z and X → Y then WX → YZ.
3. Transitive Property: If X → Y and Y → Z then X → Z.
4. Union Property: If X → Y and X → Z then X → YZ.
5. Decomposition Property: If X → YZ then X → Y and X → Z.
14

15. Reflexive Property: If X ⊇ Y then X →
Y.
1. We can verify this property as:
Let X = { A, B, C} and Y = { B, C}.
This rule says that ABC → BC.
That is, we have to show, if
t1 [ABC] = t2 [ABC], then t1 [BC] = t2 [BC].
From table, if ABC agrees for t1 and t2 then trivially
BC is agreeing.
2. Note: Reflexive property is also known as trivial dependency.
15
A B C
a1 b1 c1
a1 b1 c1
a2 b2 c2

16. Augmentation Property: If W → Z and X → Y then
WX → YZ.
 We can verify this property as:
1. W → Z means that t1[W] = t2[W]
then t1[Z} = t2[Z]
and X → Y implies t1[X] = t2[X]
then t1[Y} = t2[Y].
2. From the table on the right, it is seen that
t1[WX] = t2[WX] implies t1[YZ] = t2[YZ].
i.e. WX → YZ 16
W X Y Z
w1 x1 y1 z1
w1 x1 y1 z1

17. Transitive Property: If X → Y and Y → Z
then X → Z.
 We can verify this property as:
1. X → Y and Y → Z is given,
It means for t1 and t2,
t1[X] = t2[X] implies t1[Y] = t2[Y]
t1[Y] = t2[Y] implies t1[Z] = t2[Z].
2. From the table, it is seen that,
t1[X] = t2[X] implies t1[Z] = t2[Z].
Therefore, X -> Z. 17
X Y Z
x1 y1 z1
x1 y1 z1

18. Union Property: If X → Y and X → Z then X
→ YZ.
Proof:
 Given is X → Y and X → Z , then
 From Augmentation rule: XX → YZ
XX is union of two X, so XX = X.
 Hence, X → YZ .
18

19. Decomposition Property: If X → YZ then X → Y
and X → Z.
• Proof:
1. X → YZ, this is given.
2. YZ → Y , this is trivial dependency.
3. Therefore, X → Y, from 1 and 2 transitive rule.
4. Again X → YZ, this is given.
5. YZ → Z , this is trivial dependency.
6. Therefore, X → Z , from 4 and 5 transitive rule.
19

20. Closure of Functional Dependency
Set, F+
• Typically, database designers first specify the set of functional dependencies F that can easily
be determined from the semantics of the attributes of R; then apply axioms to infer
additional functional dependencies that will also hold on R.
• The complete set of all possible FDs that can be inferred from F is known closure of F,
denoted by F+.
• Example: Let us consider a relation R(A,B,C,D) and functional dependency set F = { A -> B,
B -> C, C -> D}. Then, F+ = { A -> B, B -> C, C->D, A->C, B ->D, A-> A,
B->B, C->C, D-> D, ........ }
• This above process of finding F+ is very tedious task. So a systematic way to determine these
additional functional dependencies is first to determine attribute closure rather than F+.
20

21. Attribute Closure
• This is set of all the attributes determined by given set of attributes.
• Example: Let us consider a relation R(A,B,C,D) and functional dependency
set F = { A -> B, C -> D, B -> C}. Then (AB)+ is attribute closure of (AB)
is all the attributes determined by AB together.
• (AB)+ = { A, B, C, D}, because A, B are added to set from reflexive
property, C and D by transitive property.
• C+ = { C, D}
• A+ = { A, B, C, D } 21

22.  Algorithm
1. Closure = X
2. Repeat until no change to Closure
For each FD: U -> V in F
do
if U ⊆ Closure then
set Closure = Closure ∪ V
End do
3. End Repeat 22
Attribute Closure

23. Example
Solution,
 Let X = {A, B}. The inner loop repeats 4 times, once for each of the given FDs.
 On the first iteration, i.e. for A → BC, we see LHS of this FD is subset of closure X, so we
add RHS of FD to closure X. B is already there, add only C. Therefore, X = {A, B, C}
 On second iteration, for E → CF, LHS is not subset of X so, X remains unchanged.
 On third iteration, for B → E, Add E to X. Now X = {A, B, C, E}
 On fourth iteration, For CD → EF, X remains unchanged.
 Now we go round the inner loop 4 times again. On the first iteration, the result does not
change does not change; On the second, it expands to {A, B, C, E, F}; On the third and
fourth iteration, it does not change.
 Now we go round the inner loop 4 times again. Closure does not change, and whole process
terminates, with (AB)+ = {A, B, C, E, F}.
23
 Suppose we are given a relation R with attributes (A,B,C,D,E,F) and FDs:
A → BC, E → CF, B → E, CD → EF. Compute: (AB)+.

24. Exercise
• Given a relation R (A, B, C, D) and a set of functional dependencies, F as
follows:
AB -> C
B -> D
D -> C
C -> A
• Find D+, C+ , B+ and A+ .
24

25. Exercise
• Given a relation R (A, B, C, D, E) and a set of functional dependencies, F as
follows:
A -> BC
CD -> E
B -> D
E -> A
• Find A+, B+ , E+ and (BC)+ .
25

26. Super Key or Candidate Key
• Super Key: A set of attributes that uniquely determines all the attributes of a
relation is known as super key.
• For example: Let a relation R(A,B,C,D) and suppose A determines all the attributes
(A, B, C, D) then A is called super key of the relation.
i.e. if A is a super key then A -> B, A -> C and A -> D.
• Candidate Key: A candidate key is also a super key but it is minimal. That is, there is
no proper subset of candidate key that is super key. If we remove any attribute from
candidate key it cannot determine all the attributes of the relation.
26

27. Finding Super Key or Candidate Key from Functional
Dependencies
 Functional dependencies are useful to find super keys or candidate keys of a
relation.
 Let us consider a relation R(A,B,C,D) and FD set F = { A -> B, C -> D}.
 Now, let us find
A+ = {A, B}
B+ = {B }
 Similarly, we can check other attribute closure to find out whether they determine
all attributes or not. We find that only AC closure does this.
(AC)+ = ( A,C,B, D)
 Obviously (ABCD)+ = (A B C D) , so (ABCD) is a super key.
 (ABC) is also super key. Since ABC -> AC by reflexive property, and also we have
found AC-> ABCD, hence, ABC -> ABCD by transitive property. Therefore, any
super set of candidate key is a super key.
 AC is a candidate key since A and C both are essential to be a super key.
27

28. Exercise
• Find the candidate key for following relation and
functional dependencies.
Relation is R(A, B, C, D) and F = { AB->C, B -> A}.
Tip: The attributes that are not in RHS of F are the essential components of candidate key.
28

29. Exercise
• Find the all the candidate keys for relation R(A, B, C, D)
with functional dependencies F = { A->B, B->C, C ->D,
CD-> B, BC ->A}.
29

30. 1NF
• The first normal form says that every attribute is an atomic in a table.
• This means that every table have no multi-valued and no composite attributes.
• The following tables are not in 1NF as first table has multiple values in course attribute and
second table has composite attribute address.
30
Sid Sname Course
1 Salim C, C++
2 Abdul C++, Java, .Net
3 Roshan Java
Eid Ename Address
1 A 221-Mitranagar-Kathmandu
2 B 223-Nayapatan-Pokhara
3 C 302-Kirtipur-Kathmandu
4 D 112-Thimi-Bhaktapur
Student
Employee

31. 1NF
• These tables are difficult to deal by using SQL.
• For example: to find number of student who take course java in above table with
sql query will be difficult.
• SQL query will not give result in desired form, we have to process the individual
value by application program.
• This complicates the query process and end user will not have sufficient knowledge
to write application program.
• Therefore, the table should be converted to 1NF.
31

32. How to convert the table to 1NF
• To convert multi-value attribute to 1NF, one way is to create separate
row for each value. This solution creates high redundancy of data.
• Another way is decompose the relation in two tables as in solution 2.
32
Solution 1
Sid Sname Course
1 Salim C
1 Salim C++
2 Abdul C++
2 Abdul Java
2 Abdul .Net
3 Roshan Java
Sid Sname
1 Salim
2 Abdul
3 Roshan
Sid Course
1 C
1 C++
2 C++
2 Java
2 .Net
3 JavaSolution 2

33. Conversion of table with composite
attribute
33
Eid Ename Address
1 A 221-Mitranagar-Kathmandu
2 B 223-Nayapatan-Pokhara
3 C 302-Kirtipur-Kathmandu
4 D 112-Thimi-Bhaktapur
Eid Ename H_No Street City
1 A 221 Mitranagar Kathmandu
2 B 223 Nayapatan Pokhara
3 C 302 Kirtipur Kathmandu
4 D 112 Thimi Bhaktapur
• To convert such table, create separate
column for each of components of
composite attribute.

34. 2NF
 A relation R is in 2NF if
i. It is in 1NF.
ii.There is no partial dependency.
 Partial dependency:
Let X be a proper subset of some candidate key and A be a non-prime attribute then,
X -> A is partial dependency. That is, a non-key attribute is functionally determined by
part of candidate key.
 In other words, a relation R is in 2NF if it is in 1NF and every non-prime OR non-key
attributes are fully functional dependent on candidate key of R.
◦ That is, no non-prime attribute should be determined by the part of candidate key.
◦ Or there should be no partial functional dependency.
 If a relation in 1NF has candidate key with single attribute, it is automatically in 2NF.
34

35. Example
 Consider a relation Inventory( Part_ID, Warehouse_ID, Quantity, Warehouse_address).
 The primary key is compound key(Part_ID, warehouse_ID).
 The attribute Quantity depends on both Part_ID and warehouse_ID.
 But Warehouse_address depends only on Warehouse_ID. This is partial dependency.
(why?)
 So, the relation Inventory is not in 2NF.
 This partial dependency is causing redundancy
in the table.
 The dependency is shown below:
35
Part_ID Warehouse_ID Quantity Warehouse_address
1 1 5 Kathmandu
1 2 3 Lalitpur
2 1 2 Kathmandu
3 1 2 Kathmandu
4 2 4 Lalitpur
Inventory
Part_ID Warehouse_ID Quantity Warehouse_address

36. DECOMPOSITION OF RELATION TO 2NF
36
INVENTORY
Part_ID Warehouse_I
D
Quantit
y
Warehouse_address
1 1 5 Kathmandu
1 2 3 Lalitpur
2 1 2 Kathmandu
3 1 2 Kathmandu
4 2 4 Lalitpur
Warehouse
Warehouse_I
D
Warehouse_address
1 Kathmandu
2 Lalitpur
INVENTORY
Part_ID Warehouse_I
D
Quantit
y
1 1 5
1 2 3
2 1 2
3 1 2

37. 2NF : Example
Consider a relation R(A,B,C,D) with F = { AB -> C, A -> D}. Test whether R
is in 2NF or not.
• Here, no attributes other than A or B can determine A or C, so candidate key must
have AB. And, (AB)+= ( A C B D), hence, AB can determine all attributes. So, AB
is candidate key.
• Are there any other possible candidate keys? Answer: NO. Why?
• A and B are called prime attributes and C and D are non-prime attributes.
• AB -> C satisfies 2NF.
• But, A -> D is partial dependency.
• So, R is not in 2NF.
37

38. Decomposing Relation into 2NF
• Create separate table for each partial dependencies.
• So, above relation R(A,B,C,D) is decomposed into R1(A,B,C) and R2( A,D).
• R1 has AB as a key and R2 has A as a key.
38
A B C D
A B C
A D
R1
R2
R

39. Exercise
1. Consider the relation R(A,B,C,D) and F = { AB -> C, B -> D}.
Find whether R is in 2NF or not.
2. Consider the relation R(A,B,C,D,E) and F = { AB -> C, A -> D,
B -> E}. Find whether R is in 2NF or not. If not decompose it
into 2NF.
39

40. 3NF
 A relation R is said to be in 3NF if
• It is in 2NF.
• No non-prime attribute of R is transitively dependent on key of R.
 Transitive Dependency:
• Let X, Y and Z be set of attributes such that X -> Y, but Y -≯ X and Y -> Z where
Z ⊆ X and Z ⊆ X , then X -> Z. X transitively determines Z or Z is transitively
depends on X.
 Transitive dependencies are the dependencies between non-prime attributes.
That is, a non-prime attribute determines another non-prime attribute.
 A relation to be 3NF no non-prime attribute should depend transitively on
some candidate key. That is, each non-key attribute should be dependent on
and only on the candidate key.
40

41. Example : 3NF
 Consider a relation Customers( CustID, CustName, CreditLimit, RepNum, RepFName,
RepLName) and inspect following data.
 CustID is primary key. The attributes CustName, CreditLimit, RepNum all depend on CustID
but RepFName and RepLName depend on RepNum.
 Here, we observe the fact that non-prime attributes depend on another non-prime attribute.
That is, transitive dependency is found. So, Customers relation is not on 3NF.
41
CustID CustName Creditlimit RepNum RepFName RepLName
101 KMC 15000 15 Ishan Maskey
202 Teaching Hospital 20000 25 Santosh Sharma
303 Manmohan Memorial 18000 15 Ishan Maskey
305 Star Hospital 12000 50 Kiran Chemjong
505 B and B 20000 25 Santosh Sharma

42. Decomposition of Customers Relation into
3NF
42
Customers
CustID CustName Creditlimit RepNum
101 KMC 15000 15
202 Teaching Hospital 20000 25
303 Manmohan Memorial 18000 15
305 Star Hospital 12000 50
505 B and B 20000 25
CustomerReps
RepNum RepFName RepLName
15 Ishan Maskey
25 Santosh Sharma
50 Kiran Chemjong
 Divide the relation Customers into two relations Customers( CustID, CustName,
CreditLimit, RepNum) and CurstomerReps ( RepNum, RepFName, RepLName).
 The division is performed based on dependencies.
CustID CustName CreditLimit RepNum RepFName RepLName

43. Example
• Consider a relation R(A,B,C,D) with FDs { AB -> C, C -> D}.
• The candidate key will contain AB. So, check (AB)+= (ABCD), this implies AB is
candidate key.
• No other candidate keys are possible. Why?
• AB are prime and CD are non-prime attributes.
• Here, non-prime attribute D is transitively dependent on candidate key AB. So, R is
not in 3NF. But R is in 2NF.
• To decompose R into 3NF, we construct relations R1(ABC) and R2(CD) with R1
having AB as key and R2 having C as key attribute.
43

44. 3NF : Alternative Definition
• A table is in 3NF, if
i. if it is in 2NF.
ii. For every non-trivial dependency X ->A, X is either super
key or ‘A’ is a prime attribute.
• Example: Consider a relation R(A,B,C) with { A -> B, B -> C}. Is
this relation in 3NF?
44

45. Example
• From the inspection of FDs, A cannot be determined by B and C. So A can be
candidate key. Find A+=(A B C), i.e. A determines all. Hence, A is candidate key.
• A is prime attribute and B, C are non-prime attributes.
• A->B and B ->C both are non trivial dependencies. Let’s check whether condition
for 3NF.
• In case of A -> B, condition is true since A is super key, although B is non prime
attribute.
• In case of B -> C, condition is false since neither B is super key nor C is prime.
• Hence, R is not in 3NF.
• Is this relation in 2NF? Answer is YES ! why?
45

46. Decomposition of Relation to 3NF
• Keep the attributes which satisfy the condition for 3NF in one relation and
not satisfying in other relations.
• Here, we construct R(A, B, C, D) into R1(A,B) and R2(B,C).
• For R1 relation A is key and R2 relation B is the key.
46

47. Exercise
 Consider the relation R(A,B,C,D, E) and F = { AB -> C, B ->D,
D ->E }. Find whether R is in 3NF or not. If not decompose it
into 3NF.
47

48. Boyce-Codd Normal Form (BCNF)
• When a relation has more than one candidate key, anomalies may result even
though the relation is in 3NF.
• 3NF does not deal satisfactorily with the case of a relation with overlapping
candidate keys
– i.e. composite candidate keys with at least one attribute in common.
• A relation is in BCNF, if for every non trivial dependency X ->A, X is
candidate key.
• If a relation is in 3NF and has single candidate key, then it is in BCNF as well.
48

49. BCNF : Example
 Consider the relation R(A,B,C,D) and F = { AB -> C, C -> D}
 Here, no attribute can catch A and B, so candidate key must have AB. Let’s
check whether AB itself is candidate key, for this, compute (AB)+= (ABCD).
 This means AB is a candidate key. A or B cannot be replaced by any other
attributes. So AB is only one candidate key.
 AB are prime attributes and CD are non-prime attributes.
 This show that C -> D is transitive dependency. Therefore, R is not in 3NF.
 Therefore, R is not in BCNF as well.
 Alternatively, for C -> D , C is not candidate key. This violates the condition
for BCNF.
 To convert to 3NF, decompose R into two relations R1(A,B,C) and R2(C,D).
 Now the relations will be in BCNF as well.
49

50. Exercise
• Determine whether relation R(A,B,C) with F = { AB -> C, C -> A} is
BCNF or not.
Solution: Here we have two candidate keys: AB and BC.
• AB -> C and C -> A both satisfy 3NF condition. How?
• But, R is not in BCNF because for C -> A, C is not candidate key.
• To get solution, decompose R into R1(B, C) and R2(C, A)
50

51. Example
STDNO MAJOR ADVISOR
123 PHYSICS EINSTEIN
123 MUSIC MOZART
456 BIOLOGY DARWIN
789 PHYSICS BOHR
999 PHYSICS EINSTEIN
51
 Consider the following relation StudMajor( StdNo, Major, Advisor) with FDs {StdNo,
Major -> Advisor, Advisor -> Major }.
 The relation has candidate keys:
{StdNo, Major} and {StdNo, Advisor}
 This relation is in 3NF since there is no any
transitive dependency i.e. non-prime to non-
prime dependency.
 But the relation is not in BCNF.

52. Problem with Previous Table and
Decomposition to BCNF
STDNO ADVISOR
123 EINSTEIN
123 MOZART
456 DARWIN
789 BOHR
999 EINSTEIN
52
PHYSICSBOHR
BIOLOGYDARWIN
MUSICMOZART
PHYSICSEINSTEIN
MAJORADVISOR
 If the record for student 456 is deleted we lose not only information on student
456 but also the fact that DARWIN advises in BIOLOGY
 We cannot record the fact that WATSON can advise on COMPUTING until we
have a student majoring in COMPUTING to whom we can assign WATSON as
an advisor.

53. Exercise
53
• A video library allows customers to borrow videos. Assume that there is only 1 of each video.
Consider the relations and FDs are given below and find what NF is this?
video(title, director, serial)
customer(name, addr, memberno)
hire(memberno, serial, date)
title -> director, serial
serial -> title
serial -> director
name, addr -> memberno
memberno -> name,addr
serial, date -> memberno

54. 4NF
• A table is in fourth normal form (4NF) if and only if it is in BCNF and
contains no more than one Multi-Valued Dependency.
• The multivalued dependencies occur when the relation is trying to represent
more than one many to many relationships.
• Then certain attributes become independent of one another, and their values
must appear in all combinations.
54

55. Multivalued Dependency
55
Smith
Jones
Cooper
Anna
John
Lila
Elsa
Chris
Employee (X)
Dependent (Y)

56. Multivalued Dependency
56
 A multivalued dependency on R, X ->>Y, says that if two tuples of
R agree on all the attributes of X, then their components in Y
may be swapped, and the result will be two tuples that are also in
the relation.
 i.e., for each value of X, the values of Y are independent of the
values of R-X-Y.

57. Example
 Let us consider the following table: Drinkers(name, addr, phones, beersLiked)
 A drinker’s phones are independent of the beers they like.
 Thus, each of a drinker’s phones appears with each of the beers they like in
all combinations.
– If a drinker has 3 phones and likes 10 beers, then the drinker has 30 tuples
– where each phone is repeated 10 times and each beer 3 times
57
name addr phones beersLiked
Sue abc p1 b1
Sue abc p2 b2
Sue abc p2 b1
Sue abc p1 b2
Drinkers Table with 2
phones and 2 beers
• Tuples Implied by name->->phones

58. Example: 4NF
• Take the following table structure as an example:
info(employee#, skills, hobbies)
• This table is difficult to maintain since adding a
new hobby requires multiple new rows
corresponding to each skill.
• This problem is created by the pair of Multi-
Valued Dependencies. employee # ->> Skills
and employee# ->> hobbies
58
employee# Skills hobbies
1 Programming Golf
1 Programming Bowling
1 Analysis Golf
1 Analysis Bowling
2 Analysis Golf
2 Analysis Gardening
2 Management Golf
2 Management Gardening

59. Decomposition
59
A much better alternative would be to
decompose INFO into two relations:
skills(employee#, skill)
hobbies(employee#, hobby)
Employee# Skill
1 Programming
1 Analysis
2 Analysis
2 management
Employee# Hobbies
1 Golf
1 Bowling
2 Golf
2 Gardening
Hobbies
Skills

60. 5NF
• A table is in fifth normal form (5NF) or Projection-Join Normal Form (PJNF) if it is in 4NF and it
does have a lossless decomposition into any number of smaller tables.
• That is, a relation is in 5NF if it is in 4NF and joining two or more decomposed relations should not
lose records nor create new records.
• Anomalies can occur in relations in 4NF if the Primary Key has three or more fields.
• There are pairwise cyclical dependencies in the primary key comprised of three or more attributes.
• Pairwise cyclical dependency means that:
• You always need to know two values (pairwise).
• For any one you must know the other two (cyclical).
60

61. Example
• Take the following table structure as an example:
buying(buyer, vendor, item)
This is used to track buyers, what they buy, and from whom
they buy.
• The question is, what do you do if Claiborne starts to sell
Jeans? The problem is there are pairwise cyclical
dependencies in the primary key.
• That is, in order to determine the item you must know the
buyer and vendor, and to determine the vendor you must
know the buyer and the item, and finally to know the buyer
you must know the vendor and the item.
61
buyer vendor Item
Sally Liz Claiborne Blouses
Mary Liz Claiborne Blouses
Sally Jordach Jeans
Mary Jordach Jeans
Sally Jordach Sneakers

62. Solution
• The solution is to break this one table into three tables;
Buyer-Vendor, Buyer-Item, and Vendor-Item.
• The decomposition is lossless decomposition.
62
vendor Item
Liz Claiborne Blouses
Jordach Jeans
Jordach Sneakers
buyer Item
Sally Blouses
Mary Blouses
Sally Jeans
Mary Jeans
Sally Sneakers
buyer vendor
Sally Liz Claiborne
Mary Liz Claiborne
Sally Jordach
Mary Jordach

63. Loss-less Join Property
• A relation R can be decomposed into a collection of relations to eliminate some
of the anomalies in the original relation R.
• Loss-less Join Decomposition: Let R be a relation and has a set of FDs ‘F’ over R.
The decomposition of R into R1 and R2 is lossless w.r.t F if R1 ⋈R2 = R
• Lossy Decomposition: if R1 ⋈ R2 contains some spurious tuples, the
decomposition is called lossy decomposition.
• The split of relations is guaranteed to be lossless if the intersection of the
attributes of the new tables is a key of at least one of them.
• The word loss in lossless refers to loss of information, not to loss of tuples.
63

64. Example of Lossy Decomposition
64
121
211
111
CBA
21
11
BA
21
11
CA
221
121
211
111
CBA
Original Relation R
Reconstruction
Decomposition

65. Example 2
• Consider an example of different subjects taught by different lectures and the lectures taking classes
for different semesters.
• All the three columns together acts as a
primary key.
• Here, Rose takes physics and mathematics
class for sem 1 but she does not take
physics class for sem 2.
• In this case, all these three fields is required
to identify valid data.
• To insert data and retrieve information will be easy
if we decompose the relation into three relations:
(subject, lecturer), (lecturer, class), (subject, class).
65
Subject Lecturer Class
Mathematics Alex Sem 1
Mathematics Rose Sem 1
Physics Rose Sem 1
Physics Josheph Sem 2
Chemistry Adam Sem 1

66. 6NF
66
 Definition: A relation schema is said to be in DKNF if all constraints and
dependencies that should hold on the valid relation states can be enforced simply by
enforcing domain constraint and key constraints on the relation.
 The idea is to specify (theoretically, at least) the “ultimate normal form” that takes into
account all possible types of dependencies and constraints. .
 To be specific, enforcing domain constraints just means checking that attribute values
are always values from the applicable domain (i.e., values of the right type); enforcing
key constraints just means checking that key values are unique.
 The practical utility of DKNF is limited.
 The sad fact is, not all relations can be reduced to DKNF; nor do we know the answer
to the question "Exactly when can a relation be so reduced?“.

67. Thank You !
67